利用柯西不等式的变式证明竞赛不等式

广东省广州市第六中学(510300) 陈霞

利用柯西不等式的变式证明竞赛不等式

广东省广州市第六中学(510300) 陈霞

本文通过实例探讨了如何基于柯西不等式的变式,解决中学竞赛中的不等式的证明问题.

柯西不等式 有理分式

中学数学竞赛中经常出现文字不等式的证明问题,而最常用的方法莫过于均值不等式了.文 [1]作者通过具体实例,说明了如何通过凑配技巧运用柯西不等式证明有理分式不等式.文中所呈现的凑配技巧可谓精彩绝伦,令人拍案叫绝.这是数学的一种美学.虽然如此,这些凑配的技巧却是不太容易掌握和运用.数学的另一种美在于抽象和统一.有没有一种较为统一的、易于掌握的方法呢?这就是柯西不等式的变式.下面我们通过具体实例加以说明.首先我们回顾一下柯西不等式的一般变式及两种特殊情形.

定理设m≥ 2,则对任意xi,ai∈(0,+∞),i= 1,2,···,n,总有

注当m=2时,将(1)式中的xi和ai分别用xiyi和替换后所得到的不等式便为柯西不等式,其中yi＞0,i=1,2,···,n

下述问题的结论是(2)式的直接推论.

例1(第 19届北欧竞赛题)设a,b,c为正数,求证:

例2(2000年加拿大奥林匹克试题)设a,b,c为正数,求证:

证明由 (3)式及均值不等式ab+bc+ca≤a2+b2+c2,得

例3设a,b,c为正数,求证

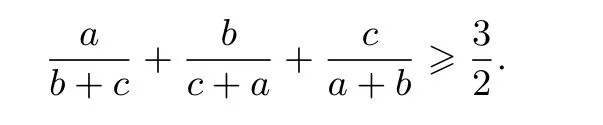
例4(文 [1]例 8,即 2009年清华大学自主招生试题)设x,y∈R+,x+y=1,求证:对任意正整数n,有

证明由 (1)式,得

证明由 (1)式,得

最后,我们来证明文 [2]中花了较长篇幅证明的一个结论,即该文中的推广2.

以上例子表明利用柯西不等式的变式来证明有理分式不等式是相对容易掌握的,因为它不需要高超的凑配技巧.当然,这种方法也有其局限性,试图用它解决所有问题是不现实的,许多问题需将它与基本不等式结合才能发挥其最大效用.

[1]王淼生.运用均值不等式的灵魂在于凑配[J].中学数学教学参考, 2013(6):57-58.

[2]李怀军,陈百华.一次“巧合”的证明与推广[J].中学数学教学参考, 2013(6):48-50.