例析函数选择压轴题的解题策略

珠海市斗门区第一中学(519100) 唐学宁

例析函数选择压轴题的解题策略

珠海市斗门区第一中学(519100) 唐学宁

函数选择压轴题由于其“数式”的变换及“形”的千姿百态,展示了它特有的数形结合思想,对培养学生的观察力,训练思维的广阔性与深刻性发挥其特有的作用.然而,高考函数选择题的得分率历年来都较低,尤其是函数选择题中的压轴题得分率更是如此.为此,笔者通过对近年来的试题进行分类解析,希望能给读者一些启示.

一、巧选特殊函数 用特殊值法

在函数问题中,如果已知条件中含有某些不确定的量,但题目暗示答案可能是一个定值时,可以将一般函数取一个特殊的函数来求出这个定值,从而达到简化求解过程的目的.

例1已知函数f(x)在R上的导函数为f′(x),若f(x)＜2f′(x)恒成立,且f(ln4)=2,则不等式f(x)＞的解集是( )

A. (ln2,+∞) B. (2ln2,+∞)

C. (−∞,ln2) D. (−∞,2ln2)

例2定义在R上的偶函数f(x)的导函数为f′(x).若对任意的实数x都有2f(x)+xf′(x)＜2恒成立,则使x2f(x)−f(1)＜x2−1成立的实数x的取值范围为( )

分析因为函数f(x)为偶函数,我最快想到的函数是f(x)=0,计算f′(x)并代入验证,发现完全满足条件2f(x)+xf′(x)＜2,因此可以直接取f(x)=0.

解令f(x)=0,计算可知满足条件,则要解的不等式x2f(x)−f(1)＜x2−1变为x2−1＞0,解之得(−∞,−1)∪(1,+∞),答案为B.

点评联系已知条件和结论,构造特殊函数是解高中数学函数选择题中的巧妙方法,如果在题目中给出奇偶性与单调性,往往取多项式函数做为特殊函数.

二、精挑选择项值 用排除法

在函数选择题中,如果一时没有什么好的思路,也可以从选择支中挑选一些值,代入题目中去验证,如果满足条件,则表示该选择支有可能就是要选的答案,这种方法对一些难、偏、繁问题有奇效.

例3已知函数f(x)=aex−x2−(3a+1)x,若函数f(x)在区间(0,ln3)上有极值,则实数a的取值范围是( )

分析观察四个选择项,可以发现,如果我们取a=−2代入验证,可以一次性排除两个答案.

解令a=−2,则f(x)=−2ex−x2+5x,得f′(x)=−2ex−2x+5,故f′(0)=−2+5=3＞0,f′(ln3)=−2×3−2ln3+5＜0,知函数f(x)在区间(0,ln3)上有极值,a=−2满足条件,排除C、D两个答案.观察A、B,发现只须选a=−1进行验证即可.此时f(x)=−ex−x2+2x,f′(x)=−ex−2x+2,而f′(0)=−1+2=1＞0,f′(ln3)=−3−2ln3+2＜0,也满足条件.因此选A答案.

点评用排除法的一般情况下要做两次,第一次在四个选择项里选值时,应选两个包含这个值,另两个不包含这个值,这样就能排除两个答案;第二次选值时怎么简单怎么选.

例4若函数f(x)=ex(sinx+acosx)在上单调递增,则实数a的取值范围是( )

A.(−∞,−1] B.(−∞,−1) C.[1,+∞) D.(1,+∞)

分析四个选择支这么有规律,不使用排除法都可惜了.取a=1可以一次排除两个答案.

解令a=1,则

点评有些同学可能观察到C、D答案全正,而A、B有正有负,因此先选a=0,然后再选a=1,这其实也是一样.在使用排除法过程中,选值非常重要,选值好,能简化运算,方便解题,选值不好,可能让整个题目繁难复杂不可计算.

三、细画函数图像 用数形结合法

“数”与“形”是数学的基本研究对象,它们之间存在着对立统一的辩证关系.数形结合思想,就是将抽象的数学语言与直观的图形结合起来,通过对图形的认识、数形转化,以提高思维的灵活性、形象性、直观性,使问题化难为易,化抽象为具体.

例5.已知函数若关于x的方程f(f(x))=a存在2个实数根,则a的取值范围为( )

A. [−24,0) B. (−∞,−24)∪[0,2)

C. (−24,3) D. (−∞,−24)∪[0,2]

分析方程f(f(x))=a是一个嵌套函数,f(x)是一个分段函数,如果直接去求f(f(x))的解析式,难度将相当大.而如果画出f(x)的图像,根据图像分析结果,难度将小很多.

解画出y=f(x)的图像如图所示,观察四个选择项,可选取a=−6.如果a=−6满足条件,则可排除B、D,否则排除A、C.由f(f(x))=−6,得f(x)=−8或f(x)=2,而f(x)=−8有两个根,f(x)=2有一个根,共3个根,因此不满足条件,排除A、C.观察B、D,选a=2,f(f(x))=2得f(x)=0,而当f(x)=0时只有一个根x=−2(x=1是空心点),所以应选答案B.

点评本题采用了数形结合与排除法,简单易行,比使用直接求函数f(f(x))的解析式要简单得多.其中选a=−6是为了更好的计算出根.

图1

例6已知函数则下列关于函数y=f[f(x)]+1的零点个数的判断正确的是( )

A. 当k＞0时,有3个零点;当k＜0时,有2个零点

B. 当k＞0时,有4个零点;当k＜0时,有1个零点

C. 无论k为何值,均有2个零点

D. 无论k为何值,均有4个零点

分析方程y=f[f(x)]+1是一个嵌套函数,求其解析式有一定难度,因此采用数形结合法.

图2

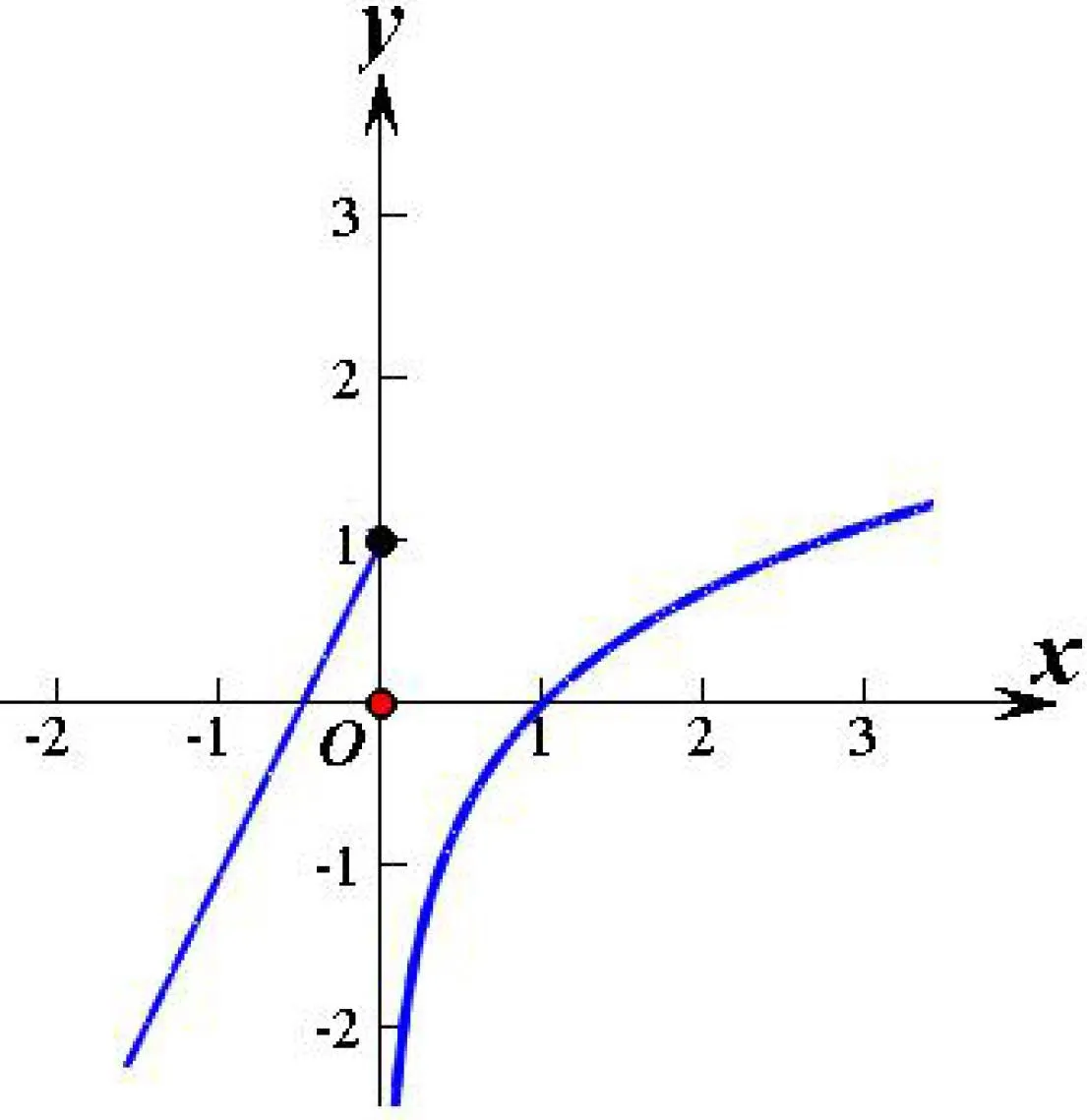
图3

解画出函数y=f(x)的图像如图所示,y=f[f(x)]+1的零点相当于求方程f[f(x)]=−1的根.当k＜0时,由f[f(x)]=−1可得f(x)≈0.5,而f(x)=0.5只有一个根.这样就可以判断答案为B.当k＞0时,由f[f(x)]=−1可得f(x)≈0.5或f(x)≈−1左右,而f(x)=0.5有两个根,f(x)=−1也有两个根,因此共有四个根.

点评本题使用了f(x)≈0.5即近似值为0.5,可以这样做的原因是:本题只要求零点个数,不需要具体的值,采用近似值可以节约时间.

四、尝试特殊位置 用试根法

函数零点问题是导数综合应用的核心问题,对于一些特殊的函数,如果适当的运用试根法,可以取得化腐朽为神奇的效果.

例7(根据2011年浙江卷理科 22题改编)设函数如果对于任意的x∈(1,3],都有f(x)≥−2e成立,则a的取值范围是( )

A.(−∞,3e]B.(−∞,1) C.[3e,+∞) D.(1,+∞)

分析要求a的取值范围,可以先使用分离变量,然后求最值的思想.

取(1,3e]中的x,使式子可以求值,自然想到x=e,代入发现果然是g′(x)=0的根.又因为函数在(1,3e]上为增函数,所以g′(x)=0有且只有x=e这个根,而x∈(1,e)时,g′(x)＜0,x∈(e,3e)时,g′(x)＞0.因此g(x)min=g(x)=3e,可知选A.

点评试根时如果是多项式函数,常用的是0,±1,±2等等,如果含有式子lnx,则常用的是等等.

综上所述,对于函数选择压轴题可以采用特殊值法、排除法、数形结合法等方法简便巧妙的选出答案;可能有部分同学认为,不直接做,而是使用上述这些方法感觉上好像没有把题目做出来一样,心里不踏实.事实上,到了高三,我们需要的是分数,高考两个小时,时间紧迫,短短的时间内要解决完大量的试题,就必须做到分秒必争,而直接做其实就是“小题大做”;只要能选出正确答案,没有人关心你是直接求的,还是用其他什么方法的解出来的.在实际解题中,必须有意识的培养这些特殊思想,平时做试卷还应该多加练习,到考场时自然熟能生巧,事半功倍.