海峡两岸初中数学教材因式分解比较研究

郑宝燕+廖金祥

[摘 要] 本文从教材内容、教材例题、教材习题方面对海峡两岸初中数学教材因式分解进行比较研究，发现台湾翰林版教材可读性较强，注重计算的基本功；人教版教材注重在例、习题的解答中形成对知识的建构.

[关键词] 因式分解；可读性；数形结合；计算能力

因式分解是整式乘法的逆向运算，它是进行数的简便运算的一种常用方法，还可以用于等式证明、整除问题、初中几何问题等，它有效地解决了二次方程和高次方程的降次问题. 因此，因式分解在整个初中代数体系，甚至在几何里的作用都举足轻重，是一个必不可少的数学解题“工具”.

海峡两岸同根同宗，由于历史原因，两岸的数学教材有一定的差异. 为研究海峡两岸初中数学教材的变化，我们申报了福建省教育科学“十二五”规划2015年度课题《闽台两岸中学数学教材例习题比较研究》，并获得立项（立项编号FJJK15-437，主持人厦门二中廖金祥）. 研究过程中，我们选取人民教育出版社（以下简称“人教版”）和台湾翰林出版社（以下简称“翰林版”）中因式分解部分作为比较内容，研究海峡两岸这部分教材内容、例题配置、习题配置情况，期望为初中数学教师和教材研究者提供借鉴与参考.

教材内容比较

通过对海峡两岸教材“因式分解”内容的比較发现，人教版教材因式分解内容较基础，篇幅少，共8页；台湾翰林版教材内容丰富，篇幅多，共36页. 其中，提公因式法和公式法等基础知识是共同的部分，翰林版教材增加了分组提公因式法和十字交乘法等，它们正是我们新课程改革删去的内容，这些内容要求比较高，技巧性强. 人教版教材贯彻了新课程标准的基本理念，删去了传统教材中的分组分解法和十字相乘法等内容. 十字相乘法虽然没有具体的课时安排，但它出现在教材中的阅读与思考部分. 为了让学生明确因式分解的意义，台湾翰林版教材编撰了因式与倍式、因式分解的意义这两个课时内容，类比因数、倍数、列算式等小学的知识内容来介绍因式、倍式. 例如，（x2-4x+3）÷（x-3）=x-1，余式为0，因为x-3能整除x2-4x+3，就称x-3是x2-4x+3的因式，而x2-4x+3是x-3的倍式.

由上面的例子我们可以知道：（x2-4x+3）=（x-3）（x-1）. 而人教版教材是从整式乘法逆向思维的角度简单介绍因式分解的概念的.

教材例题比较

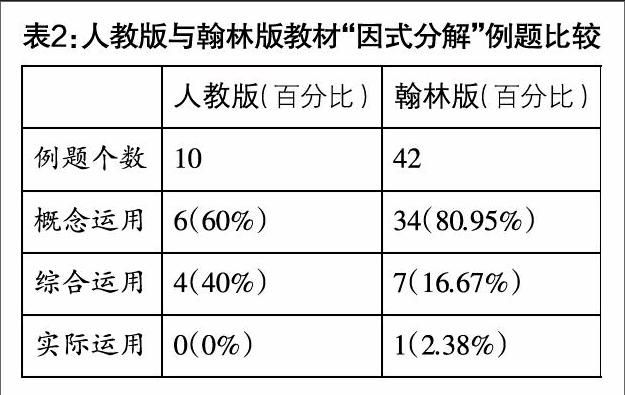
初中教材中的例题都是经过专家精挑细选的，具有很强的示范和导向作用. 例题可以让学生理解和掌握数学知识与概念，发展数学能力. 由表2可知，在因式分解部分，人教版教材例题明显比台湾翰林版教材少，仅约其四分之一，台湾翰林版教材，每出现一个新的知识点，就会设置所有可能类型的例题去应用这个知识，而人教版教材例题的设置仅是对所学知识的简单介绍，需要学生在解答课后习题时才会发现对所学知识的应用.

例如，台湾翰林版教材中提公因式法这个知识点就设置了提单项公因式、提多项式公因式、变号提公因式、分组提公因式、重新分组提公因式等类型的例题，而人教版教材仅仅只设置了两道例题，需教师和学生进行归类、整理.

教材习题比较

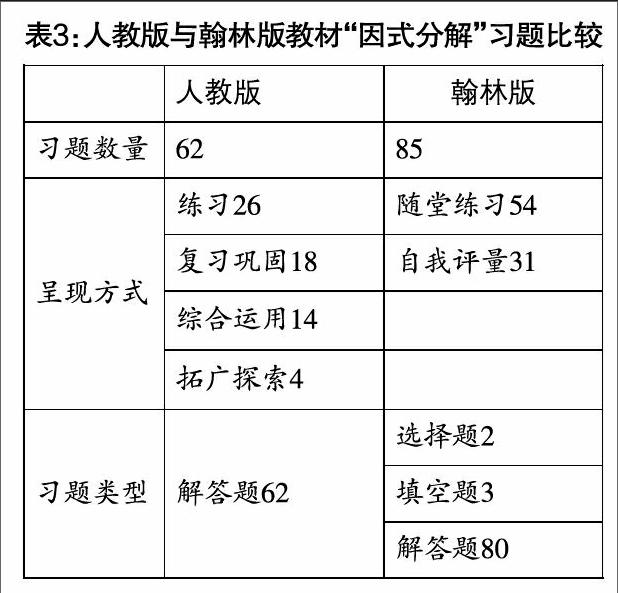
翰林版教材容量比人教版教材内容多，由表3分析可知，翰林版教材习题也比人教版教材习题多. 人教版教材习题有两类——练习题和习题，练习题较基础，供课堂使用，巩固所学的基础知识；习题位于因式分解这一大节之后，根据难度分为复习巩固、综合运用、拓广探索，综合运用和拓广探索的难度明显高于复习巩固，供学有余力的学生选做. 人教版教材因式分解习题除了注重基础性，还注重与其他学科、实际应用问题相结合，意在培养学生运用因式分解的知识和方法进行简便运算，从而解决实际问题. 台湾翰林版教材习题有两类——随堂练习和自我评量，每个例题之后都配有随堂练习题，例题和紧接着的练习都是类似的，对所学例题起巩固落实的作用. 台湾翰林版教材中因式分解习题总体上比较基础，重视数学计算基本功.

启示

1. 增设与小学知识衔接的相关内容，提高教材的可读性

台湾《纲要》明确提出：“在编撰教材时，必须注意数学内部连接的贯串，以强调解题能力的培养. ”因此，台湾翰林版教材的编撰以学生如何学习、乐于学习为基础，以小学的数学知识为出发点，注重学生数学知识的衔接，注重学生数学知识的探究和形成过程. 基于新课程标准的要求，人教版教材更注重学生在实际解答过程中构建新知. 为了提高学生数学知识的一贯性，促进学生对因式分解这个概念的认知和意义，我们在教材编撰中可适当增加与小学知识衔接的相关内容，满足学生的主体意愿和需要，同时提高教材的可读性.

2. 增设利用因式分解解决的几何模型题，提高学生的数形结合能力

台湾翰林版教材在因式分解章节开篇，用瓷砖铺设计算正方形墙的边长作为导入，引入因式分解章节知识，特别是例8因式分解的几何意义：如图1所示，有4个长方形，面积分别是xy，2x，3y，6，在不重叠的情况下，这4个长方形可以紧密地排出一个大长方形，已知这个大长方形的长为（y+2），求宽.

这道例题运用矩形纸片拼成图形，利用因式分解计算边的长，解决实际问题，而人教版教材没有此类型的例题. 可见，台湾翰林版教材注重学生动手拼图能力的培养，注重利用图形来解释因式分解. 在拼图的过程中，由于拼图的模式和拼图方法的不同，结论有时不唯一，所以具有相对的开放性. 为了帮助学生理清因式分解中的各种数量关系，教学中，我们可以采用数形结合法，帮助学生把握因式分解问题的本质，拓展学生的思维能力.

3. 丰富十字相乘法，提高学生的计算能力和未来竞争力

台湾翰林版教材在“利用十字交乘法因式分解”这一节中，编撰了二次项系数为1的十字交乘法、二次项系数不为1的十字交乘法，篇幅多，类型完整，内容丰富，人教版教材只是将二次项系数为1的十字相乘法设置在阅读与思考部分，类型简单，习题单一. 有人认为：十字相乘法技巧性过强，会加重学生的负担，与新课程理念相违背；也有人认为：这是一种运算工具，简洁、高效，能提高学生的解题速度，增强学生学习的信心. 笔者认为，“十字相乘法”作为一种数学工具和数学思想方法，需要学生了解，作为一线教师，可以根据学生的接受程度适当传授. 十字相乘法在高中数学计算中应用广泛，编写适当的十字相乘法学习材料，供给学有余力的学生使用，有利于提高学生的计算能力和高中学习适应能力.