A公司持有B公司可转股债券的估值案例分析

蒋骁 林立

一、案例基本情况

（一）交易情况

A公司（委托方）为加强与B公司（目标公司，为香港某上市公司）的业务合作，与B公司于2014年8月签订认购协议。根据认购协议，委托方认购目标公司于发行日定向发行的本金为700,000,000港元的可转股债券。协议约定：该可转股债券可按初步转股价格3.39港元（可予调整）兑换206,489,675股新股份。协议的转股“条款及条件”还约定：如果目标公司的股票收盘价连续10个交易日超过转股价格的200%，且日均成交金额不低于30,000,000港元，那么“售回事件”触发，即目标公司有权自可转股债券首次发行日期第一个周年日起90日期间强制发行兑换股份。目标公司于2014年10月的公告披露：根据可转股债券的条款及条件，“售回事件”已发生。

据委托方介绍以及目标公司于2014年10月发布的公告，目标公司的股票在二级市场交易不活跃，股价可能存在大幅度波动。因此，委托方与C公司（结算对手）还签订了一份结算协议，约定了标的资产的转让和结算条款及条件。该结算协议与认购协议同一天签订，包括投资方结算价格（Investor’s Settlement Price，ISP）、对手方结算价格（Counterparties’ Settlement Price，CSP）和三种结算方式（ISP和CSP全额对换、ISP和CSP净值对换，以及标的资产和CSP交易）等条款的设定；但是，根据已经触发的“售回事件”和实际可能发生的经济行为，委托方在可转股债券转换成股票后，很可能选择将标的资产出让给结算对手。因为可转债全部转为股票后，将兑换206,489,675股新股份，约占目标公司总股份的12%，如此大份额股权交易不可能在二级市场实现。如果按照结算方式的第三种情况处理，那么结算条款可以简化为：在结算日，标的资产归结算对手所有，结算对手支付给委托方一个结算价格（CSP的附属收入）。附属收入（Ancillary Amount）是指与标的资产有关的归委托方占有的任何收益，本案例中只包含委托方持有可转股债券期间的利息收入。

（二）标的资产

本次估值的标的资产是一项金融资产——可转股债券。该可转股债券由B公司于2014年9月向A公司定向发行，本金为700,000,000港元，计息年利率为三个月香港银行同业拆借利率加5.5%（按365日基准累计），到期日为首次发行日之后的第716日。合同约定初步转股价格为3.39港元（可予调整）。B公司承诺：在债券存续期间，将按照约定的利息支付方式向A公司支付利息。

本次估值对象为本金700,000,000港元的可转股债券的市场价值，估值范围包括：该债券基准日之后的利息收入，以及转换成股票后可能发生股权转让之经济行为的结算收益。本次估值基准日为2014年12月31日。

二、估值分析

（一）估值方法

经分析，鉴于标的资产是一款可转股债券，要确定它的市场价值，资产基础法不适合；另外由于该债券是目标公司向委托方定向发行、交易结构设计具有特定针对性的金融工具，市场上难以找到类似的可转股债券进行比较，所以市场法也不合适。因此，采用收益法对标的资产进行估值相对比较合理。

关于普通债券市场价值，一般是对债券未来现金流进行折现；而对可转股债券的估值，目前普遍的做法是将其分为普通债券和附着其上的看涨期权两部分，通过计算普通债券价值和期权价值，得出可转股债权的总体价值。

但是，在此次估值项目中，标的资产与传统意义的可转债不同：首先，“售回事件”的触发，使得转股的主动权转移到了目标公司，也就是说，委托方持有可转债的“转股权”是带有一定限制的权利；其次，委托方与结算对手方签订的结算协议，一方面降低了未来收益的风险和波动性，另一方面也减少了期权的价值。因此，鉴于标的资产的特殊性，我们认为将可转债的认购协议和结算协议统一考虑更符合实际经济行为，在此前提下通过估算标的资产的未来现金流量，并以合适的折现率计算该现金流在估值基准日的现值。

（二）估值假设

基于委托方与目标公司的认购合同、委托方与结算对手的结算协议、相关上市公司的公开信息，以及委托方陈述的客观经济行为，本次估值对标的资产及其附着收益的未来状况做如下假定：

1.委托方持有该可转股债券至合同约定转股日，且在转股日全部转为股票；

2.该债券持有期间的利息收入按约定兑现，且基准日之前的利息收入已结转；

3.该债券在转为股票后，考虑到目标公司的股票在二级市场交易不活跃，因此委托方有很大可能性将全部股权出让给结算对手，且该股权转让之行为能够顺利实现。

（三）估值思路

收益法的基本思路是通过估算标的资产在未来持有期间的预期收益，采用适当的折现率折算成现时价值，以确定估值对象价值的估值方法。本案例中，标的资产未来持有期间的预期收益，主要由两部分构成：一是可转债持有期间的利息收入，二是转股后股权转让的结算收益。因此，标的资产价值＝利息收入现金流折现+股权转让结算收益折现，即：

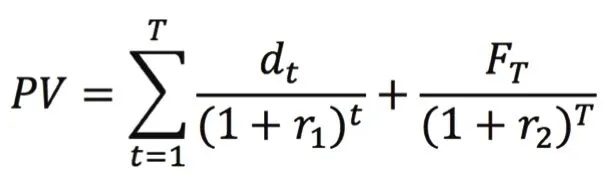
其中，r1、r2分别为所选取的利息收入和结算收益的折现率；dt、Fr分别未来第t期的利息收入和T期的股权转让结算收益；T是可转债转股并结算的日期周期。

（四）估值难点

本案例中采用收益法对标的资产进行估值，关键在于对未来收益的预测。关于标的资产债券部分的利息收入，我们认为能够按照认购协议确定；关于股权转让的结算收益，则有赖于未来目标公司的股票价格。按照结算协议，结算日前五天目标公司股票收盘价均值是一个重要参数。因此，对目标公司未来股票价格进行模拟是本次估值工作的一个重要环节。

1.股票公允价值的模拟模型

几何布朗运动是连续时间情况下的随机过程，其中随机变量的对数遵循布朗运动。几何布朗运动在金融数学中有着广泛地运用，通常用以模拟股票价格。假设目标公司的股票价格遵循几何布朗运动（Geometric Brownian Motion）规律，股价在时间序列上运动的路径由以下公式决定：

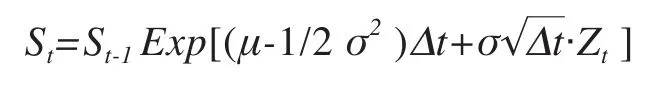
其中，St代表t时刻的股票价格，μ是该股票的年化收益率，σ是该股票的年化波动率，Zt是t时刻的一个冲击，随机变量Z一般服从标准正态分布。

2.初始公允股价S0

根据目标公司公开信息显示：该公司于2014年10月10日，有十七名股东共持有558,848,615股该公司股份，相当于该公司已发行股本的37.60%；有关股权连同由该公司三名主要股东所持有的833,987,840股（占已发行股份56.11%），相当于该公司在2014年10月10日已发行股份总额之93.71%。因此，该公司只有93,392,145股（占已发行股份6.29%）由其他投资者持有。鉴于股权高度集中，目标公司的股票在二级市场交易不活跃，股价波动幅度较大，其二级市场的股票价值不宜作为基准日公允股价的参考依据。

经与委托方充分沟通，各方认为可以将认购协议转股价3.39港元作为可转债发行日的目标公司公允股价。理由在于，协议转股价是基于公开市场条件下、交易双方自愿达成的成交价格，可以视为公允。所以，本案例将该认购协议转股价3.39港元/股作为目标公司于可转债发行日2014年9月12日的初始公允股价，并从该时点起对目标公司的公允股价进行模拟。

3.年化收益率和年化波动率

根据上市公司行业分类，目标公司属于“金融业——其他金融” （非银行/非保险）板块。经查询，该板块共有80家上市公司。本报告采用这80家上市公司于基准日前5年的数据，计算该板块的平均年化收益率和年化波动率。

经计算，该板块的年化收益率和年化波动率分别为21.09%和73.70%。

选用行业的年化收益率和年化波动率代替目标企业自身的相关参数，是因为目标企业股票交易不活跃、股权比例高度集中、近期股价波动幅度较大；另外经分析，目标企业的年化收益率和年化波动率对样本区间（时间跨度）非常敏感，基准日前一年（2014年1月1日——2014年12月31日）和发行日前一年（2013年9月13日——2014年9月12日），尽管在时间上仅相隔3个月不到，但两个区间相关参数的计算结果相差很大，与股票市场的正常运行规律不符。同时也印证了目标企业股票的二级市场交易价格不能直接作为其股价的公允价值。

选取历史五年（60个月）的样本区间，是出于两点考虑：一是宏观经济周期，尽可能地涵盖行业发展的波峰和波谷，更加准确地预测年化收益率；二是样本区间选取尽可能地体现稳健性。对于行业而言，选取若干时间点往前推五年，计算得出的年化收益率和年化波动率都较为接近，即计算的参数对样本区间选取不敏感。

4.蒙特卡罗模拟

按照以上设定的参数，本案例应用蒙特卡罗方法模拟了目标公司未来的股价。以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗模拟的基本思想。我们模拟“试验”次数为5000次。一年按245个交易日计算，即

需要说明的是，目标公司2014年10月的公告披露：根据可转股债券的条款及条件，“售回事件”已发生，目标公司有权自可转股债券首次发行日期第一个周年日起90日期间（以下简称“转股窗口”）发行兑换股份。由于“售回事件”已触发，债券转成股票的主动权已转移到目标公司，因此转股的日期具有不确定性。为了使得估值结论更加合理，本案例考虑到了该不确定性：假设转股日期是一个随机变量，且在“转股窗口”（每月按20个交易日计算，三个月60个交易日）服从均匀分布，即在（0，60）随机生成一个整数，得到一个转股日Ti，然后计算一次标的资产价值。如此循环做1000次，即i=1000，最后计算一个均值

（五）估值过程

1.未来现金流的预测

在模拟股价的基础上，依据相关条款的约定，我们预测标的资产的未来现金流量。在此，我们假设可转股日和结算日非常接近，而转股日设定在“转股窗口”随机出现。未来现金流分为两部分，转股日之前收到的利息和转股日时刻的应得未付利息加股权转让的结算收益。

利息收入：据了解，委托方部分利息收入在基准日之前已按约定支付。因此本案例所指的持有可转债的利息收入，是指在基准日之后至转股日期间的利息。根据协议约定，年利率按照估值基准日三个月香港银行间同业拆借利率加5.5%（以365日为基准累计）。

转成股票后出让股票的结算收益：可转债在转股日全部转为股票后，考虑到该股票在二级市场交易不活跃，因此委托方有很大可能性将全部股权出让给结算协议对手。因此本案例对于结算收益的计算将以协议处理方式（Methods of Settlement）的第三种情形被执行作为假设前提，即标的资产从持有方（Investor）转让给对手方（Counterparties），支付价格按协议计算。该结算协议依赖于未来股价状态，其约定的计算方式及相关参数如下：

A.收盘价（CP，Closing Price）

B.平均收盘价（ACP，转股执行日前5个交易日收盘价格的平均数）：平均收盘价的计算方式采用上述“4.估值难点”中所描述的蒙特卡罗模拟。

C.对手方结算价格（CSP，Counterparties’Settlement Price）。

●最低保证价格（GMP，Guaranteed Minimum Price）

ACP≤GMP→GMP=3.39×(1+12%-Premium Rate)

（Premium Rate指结算前标的资产的溢价率）

● 经调整的保证价格（AP，Adjusted Price）

ACP×80%＞GMP→AP=GMP+(ACP×80%-GMP)×50%

D.投资方结算价格（ISP，Investor’s Settlement Price）。

●ACP

●

ACP×80%≤GMP≤ACP→ISP=GMP

●GMP

我们对以上结算条件进行了详细分析和总结归类，以寻求投资方结算价格和对手方结算价格的一致性。假设在委托方全部股权出让前，目标公司无股票分红等影响股价之经济行为，而委托方有关标的资产的溢价（Premium Rate）也仅限于利息收入，那么以上各结算条件下的收益函数可以简化为：

GMP≥ACP×80%→Payoff=GMP

GMP(AP)

2.折现率的确定

A.利息收入的折现率：市场债务风险溢价在很大程度上受到债务评级的影响，而目标公司无公开债务评级信息，也没有同类型可比债券收益率。本报告中，依据目标公司中报公布的发行可转债的综合成本利息收入的折现率，按照9.9%计算；

B.转股收益的折现率：本案例中，根据委托方的公开股价，我们使用资本资产定价模型（CAPM）估算其股权回报率。经计算，转股收益的折现率为11.37%。该折现率的计算过程本案例中不再赘述。

3.估值计算

本案例中，无论是未来股价的公允价值，还是可转债转股的窗口期以及转股后的股权结算方式，均存在比较复杂的随机性或者假设条件，且这些随机性和假设条件前后关联。在这种情况下，我们采取编程的方式，对标的资产的公允价值进行测算。

经过以上分析并通过MATLAB编程测算，A公司所持有B公司发行的本金为700,000,000港元可转股债券，在估值基准日的市场价值是784,720,000港元（取整）。

三、案例分析

本案例的估值标的为一项可转债，属于比较典型的金融资产公允价值的估算。在案例分析过程中，我们发现，由于认购协议以及结算协议的条款设定，该项金融资产具有较大的特殊性，而这些特殊性对该项金融资产的公允价值产生了重大影响。

首先，目前对于可转债一般采用看涨期权的方式进行估值，但是在本案例中，售回条件于基准日已经触发，使得行使转股的权利不再掌握在委托方手中，使用看涨期权对可转债进行估值的前提不复存在。

其次，转股的时间是一个区间，而不是特定的日期，这使得转股日标的资产的公允价值存在不确定性。

再次，委托方在认购协议之外又与第三方结算对手签订了结算协议。通过与委托方的沟通，实行转股后委托方基本明确会根据结算协议将股权同时转让给第三方结算对手。结算价格的判断和测算又基于比较复杂的条件，且该条件与目标公司未来的股价息息相关。

最后，目标公司的绝大多数股份掌握在少数几个股东手中，股票交易在二级市场不活跃，且存在很大的波动。这对我们预测目标公司未来的股价带来了较大的难度。

基于以上分析，在本案例中，我们采用了一定的金融资产定价模型，结合目标公司所处行业的股价波动率和收益率，通过对随机游走过程的蒙特卡罗模拟，来近似确定目标公司的未来股价，并在该模型基础上对转股日期再进行模拟测算，最后结合委托方与第三方结算对手的结算条件，确定委托方完成转股并结算的经济行为所能获得的收益。这是我们对该项金融资产公允价值测算的核心内容。

我们认为，金融资产公允价值的测算一直以来都是难点，主要就在于金融资产的定价方式较为复杂、价格波动难以预计，大多数情况下都涉及到非常规的估值方式。在本案例中，我们通过详细分析标的金融资产的形成、衍变以及结算过程，将其逐一转化为量化模型，并通过计算机编程的方式简化估值逻辑的复杂度、大幅降低人力运算工作，最终在较短的时间内完成上百万次模拟计算，得到标的金融资产在大概率下的较为公允的市场价值，不失为对金融资产评估方式的一次有益探索。