赏析洛必达法则简解高考题
2017-06-05甘肃省兰州市兰化一中730060
数理化解题研究 2017年13期
甘肃省兰州市兰化一中(730060)
梁宗明●
赏析洛必达法则简解高考题
甘肃省兰州市兰化一中(730060)
梁宗明●

分离参数;洛必达法则;洛必达法则
定理:若函数f(x)和g(x)满足:

②在点x0的某空心邻域U0(x0)内可导,且g′(x)≠0;


例1 (2016全国Ⅱ)已知函数f(x)=(x+1)lnx-a(x-1).
(Ⅰ)略.(Ⅱ)若当x∈(1,+)时,f(x)>0,求a的取值范围.
解析 依据条件容易分离参数a,由f(x)>0,(x+1)lnx-a(x-1)>0,因为x∈(1,+),所以x-1∈(0,+),故.令,则.
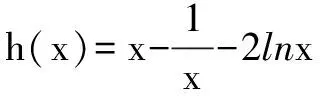
例2 (2010新课标)已知函数f(x)=ex-1-x-ax2.
(Ⅰ)略.(Ⅱ)若当x∈[0,+)时,f(x)≥0,求a的取值范围.
解析 依据条件容易分离参数a,当x∈[0,+)时,f(x)≥0,即ex-1-x-ax2≥0.
①当x=0时,a∈R.
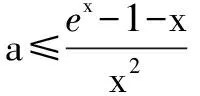
令h(x)=(x-2)ex+x+2,h′(x)=(x-1)ex+1,h″(x)=xex>0,所以h′(x)在x>0时为增函数,h′(x)>h′(0)=0,所以h(x)在x>0时为增函数,h(x)>h(0)=0.所以g′(x)>0,所以g(x)在x>0时为增函数.
用洛必达法则解决这类问题,思维难度明显降低,思路流畅、清晰,易于完美解决此类问题.
G632
B
1008-0333(2017)13-0029-01
