对流换热系数对熨平板焊接变形和应力的影响

张华清，房元斌，王伟伟

（1.徐工集团道路机械分公司，江苏徐州221004；2.江苏徐州工程机械研究院，江苏徐州221004；3.徐州徐工液压件有限公司，江苏徐州221004）

对流换热系数对熨平板焊接变形和应力的影响

张华清1，房元斌2，王伟伟3

（1.徐工集团道路机械分公司，江苏徐州221004；2.江苏徐州工程机械研究院，江苏徐州221004；3.徐州徐工液压件有限公司，江苏徐州221004）

采用有限元模拟不同对流换热系数下熨平板的焊后变形和应力分布，并采用塞尺和X射线法进行试验验证。结果表明：整体变形趋势为U形板呈“鼓泡”状，左连接板伸出端向x正向收缩变形，两侧板自由边向内收缩变形。最大变形位置出现在连接板伸出端最上端，对流换热系数为采用曲线加载时，变形误差为34.3%，系数为0.02时，误差为17.1%；不同对流散热系数对残余应力峰值影响很小，应力分布与对流换热系数为0.02时趋势一致，误差为32.6%，采用曲线加载，不考虑低应力区结果，误差为21.1%，均满足工程应用要求，证明了模拟结果的准确性。两种加载方式均满足焊接变形预测要求，在焊缝较多、应力分布复杂的情况下，应力预测建议采用曲线加载方式，反之则采用系数为0.02加载。

散热系数；有限元；焊接变形；应力

0 前言

熨平板是摊铺机熨平沥青的核心结构件，其焊接质量直接影响后续机加工、装配精度，甚至影响摊铺平整度。焊接变形和残余应力都会在生产和工作中影响平面度。对熨平板的结构设计和工艺研究主要依靠设计人员和工艺技术人员长时间的经验积累，但是人员流动、产品更新换代、技术不断完善等因素，要求在生产中不靠经验依然能够预测设计改进和工艺优化后熨平板的变形趋势和应力分布情况。焊接数值模拟技术能够有效解决这一问题。国内外专家学者已经对热源模型、功率参数、拘束条件等影响焊接变形和应力的因素进行了大量的研究[1-4]，但是对于对流换热系数研究较少。

在此以熨平板为研究对象，采用热弹塑性法，借助有限元分析手段，获得并对比分析不同对流换热系数下熨平板的焊后变形和残余应力分布，并采用塞尺测量焊后变形，辅以X射线衍射法对残余应力进行试验验证。

1 建立有限元模型

1.1 焊接工艺参数

熨平板材料为Q345B钢板，箱型结构尺寸为1 500 mm×35 mm×250 mm，一侧连接板高410 mm，现场焊接用样件如图1所示。采用松下YD-350KR2型焊机焊接，选用ER50-6实心焊丝，保护气为CO2，钢板不开坡口。焊接工艺参数见表1。

图1 熨平板模型Fig.1 Screed model

表1 焊接工艺参数Table 1 Process parameters welding

1.2 材料参数的建立

利用JMATPRO软件分析获得模拟用材料Q345B材料参数，随温度变化的部分物性参数和力学参数如图2所示。

1.3 网格模型的建立

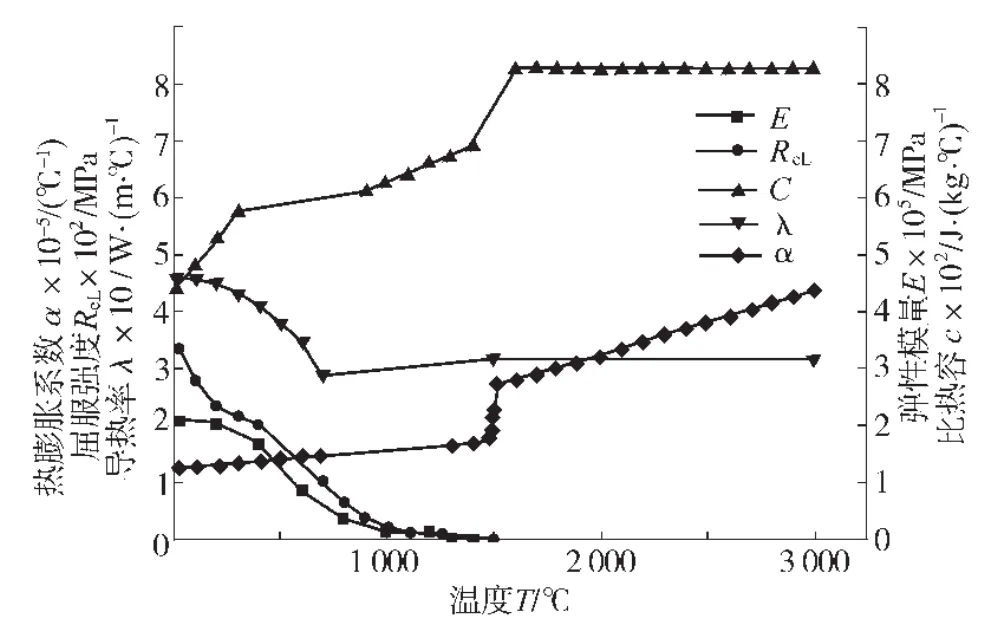
图2 Q345B钢的相关热力学参数与温度的关系Fig.2 Relationship between thermo-mechanical parameters and temperature of Q345B

为了更好平衡计算效率和计算精度，采用过渡网格划分技术，有效控制模型的网格总数，同时兼顾温度梯度和应力场计算结果可靠性，对焊缝和热影响区一定范围内的网格进行加密处理，而对自由端和远离焊缝位置采用稀疏网格[5]。获得熨平板网格模型如图3所示，其中，焊缝位置单元尺寸为2 mm，单元总数106 631个，节点数152 153个。

图3 有限元模型Fig.3 FE model

1.4 热源模型的建立

忽略焊接过程中熔池流动，采用单元生死技术，焊缝单元采用预先填充方式。为保证应力场求解精度，建立适用CO2气保焊的双椭球热源模型[6]。按照焊接工艺设计要求，对熨平板中长直且接头设计形式较多的典型接头进行试验，分别获得焊脚高度为6 mm、7 mm和双侧不同焊脚高度的热源宏观形貌，如图4所示。通过试验测量获得焊高、熔宽、熔深以及热影响区等参数。

1.5 力学边界条件

力学边界条件是指设置4组接触对来模拟熨平板焊接过程中不同面与焊接平台之间的接触关系。沿熨平板U形板x轴方向在中截面表面选择若干节点限制x向的位移；在连接板上沿连接板与U形板平行焊缝的两侧自由端中截面选择若干节点来限制xz向的位移。

图4 热源宏观形貌Fig.4 Heat resource

1.6 对流换热系数定义

焊接是一个非线性瞬态传热问题，根据傅立叶定律和能量守恒定理可得三维条件下控制方程[7-8]

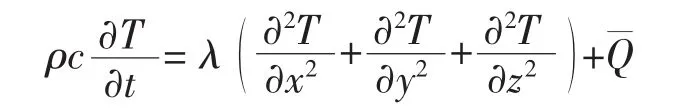
式中 T为温度；ρ为材料密度；c为材料比热容；λ为材料导热系数，材料各向同性，其中ρ、c、λ随温度变化而变化；Q为内热源强度。

温度边界条件包括熨平板表面与周围介质热交换[9]。散热表面条件：

在对流换热边界条件上

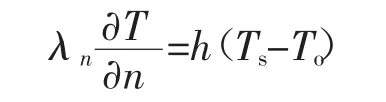
在辐射换热边界条件上

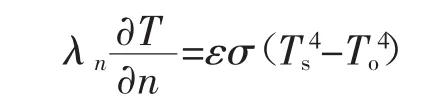
式中 n为熨平板外法线方向；λn为法线方向导热系数；h为对流换热系数；ε为发射率；σ为斯忒藩-玻尔兹曼常量；To为环境温度；Ts为边界温度。

对流换热系数分别设定为以下两种情况：

（1）考虑对流换热系数随温度变化曲线

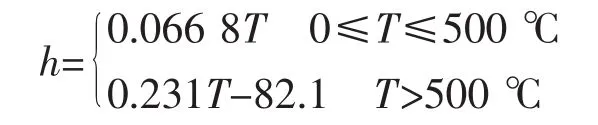
（2）利用牛顿法则和波尔茨曼定律分别考虑工件与外部环境的对流和辐射，对流换热系数设为0.02，环境温度为20℃。

2 焊接结果分析和验证

2.1 模拟温度场和应力场结果分析

计算获得不同对流换热系数下熨平板结构件焊后变形云图，如图5所示。

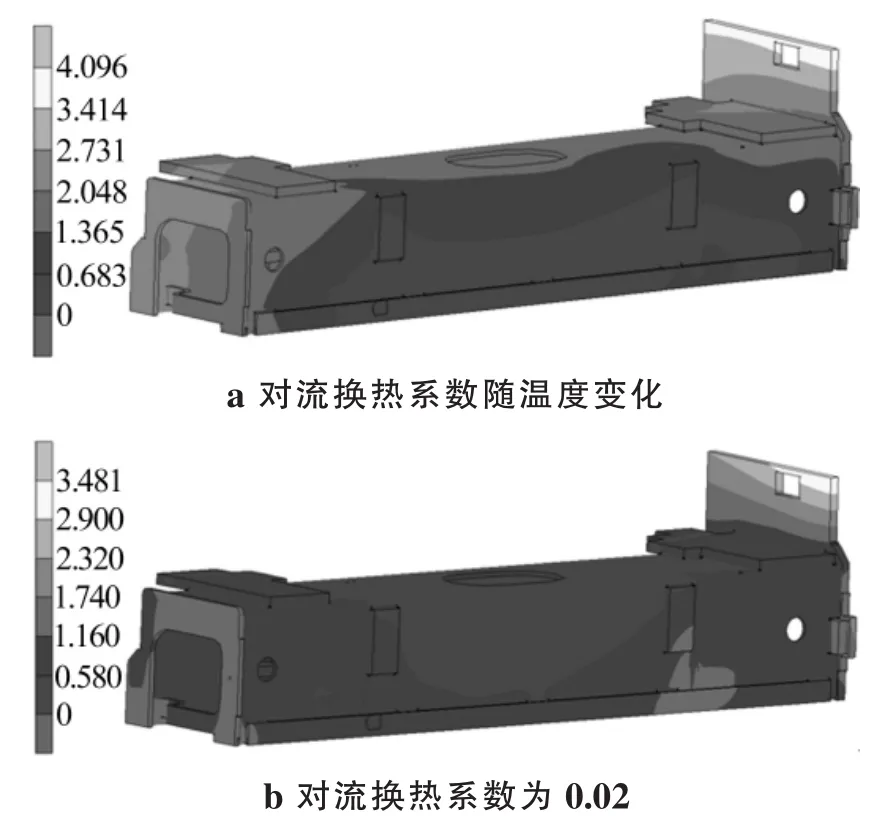
图5 焊接变形云图Fig.5 Contour of welding deformation

由图5可知，两种对流换热系数下计算得到的熨平板焊后变形趋势和最大峰值相近。按照左连接板伸出端向上，xy平面与平台接触方式放置，熨平板的整体变形趋势为：U形板呈现“鼓泡”状变形，左连接板伸出端向x正向收缩变形，在两侧板位置的自由边均向内收缩变形。

“鼓泡”状变形主要是受两侧板焊后收缩变形引起，而U形板中间上表面由于没有焊道，受到周围拘束作用而向上凸起变形。左连接板伸出端向x正向收缩变形，是由于左连接板内侧焊缝冷却后的收缩力使其发生角变形所致。在两侧板位置的自由边采用双面焊接，使其发生角变形，自由端而朝向焊缝位置侧发生角变形。最大变形位置均出现在左侧连接板伸出端最上侧，系数以曲线加载时，峰值为4.096 mm；系数为0.02时，变形峰值为3.481 mm。从理论上分析，系数0.02为等效值，加之有限元模型的建立在一种理想状态下，获得接头的结果应与随温度曲线加载相近，但是会有一些“强冷”的效果。但由分析结果可知，焊后变形在曲线加载时会更大。说明变形可能与结构形式、边界条件有关，但需要做单因素变量分析，在此不再深入研究。

焊后变形的结果是底平面变形较大的位置出现在靠近两端连接板处，呈现对角变形大的趋势。对应对流换热系数为曲线加载时的情况，焊后变形峰值为2.821 mm；系数为0.02时，焊后变形峰值为2.459 mm。考虑这部分的变形主要是其平面变形影响后续工序。

应力云图由图6所示，应力分布趋势相同且峰值相近，在焊缝位置附近应力较大。系数为曲线加载时，应力峰值为448.1 MPa；系数为0.02时，峰值为452.1 MPa。不同对流散热系数对残余应力峰值影响很小。

图6 应力云图Fig.6 Stress distribution

2.2 试验结果验证与对比分析

采用塞尺测量U形板底平面变形，如图7所示。设计3组试验样件，分别测量3组试验焊后变形，通过测量整个底平面最大位置，发现最大变形均出现在靠近两端连接板处，与仿真趋势保持一致。测量值如表2所示。

图7 变形测量Fig.7 Measuring deformation

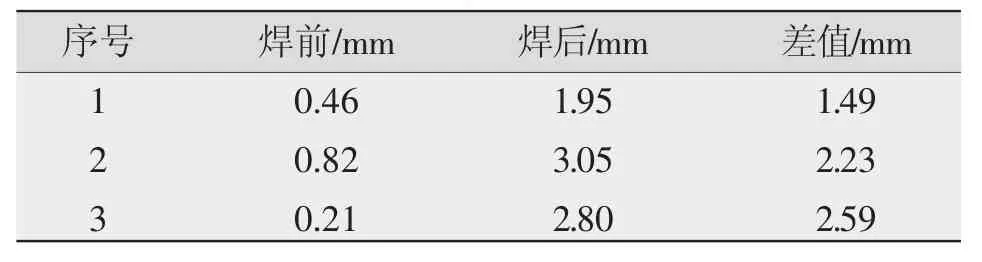
表2 变形测量值Table 2 Measuring value of deformation

由表2可知，焊接变形平均值为2.10 mm。系数为曲线加载时，误差为34.3%；系数为0.02时，误差为17.1%，满足工程应用要求，证明了模拟结果的准确性。对流换热系数为0.02时，更接近实际变形的测量结果。为避免结构件破坏，残余应力分布的试验验证采用无损残余应力测量，距离A点的距离分别为53 mm、127 mm、149 mm、488 mm、510 mm、828 mm、849 mm、1 316 mm，见图8a。由图8b可知，应力分布与对流换热系数为0.02时趋势一致，误差为32.6%，满足工程应用要求；而采用曲线加载时，低应力区出现较大偏差，不考虑低应力区结果，误差为21.1%。在高应力区测量时，X射线衍射法塑性应变导致晶格尺寸的畸形变化，使得测得的应力值增加较多，从而导致结果偏大。

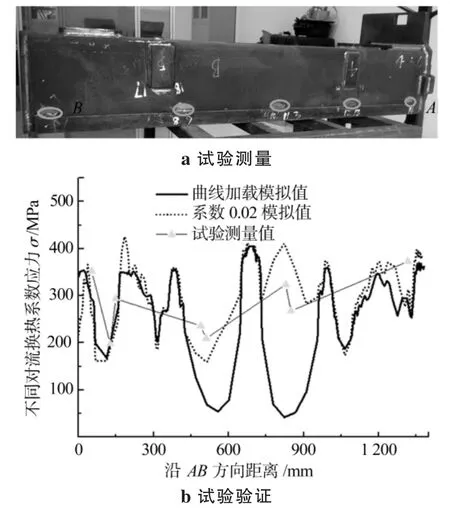
图8 试验测量和验证Fig.8 Measuring and verifying experiment

3 结论

（1）最大变形位置均出现在左侧连接板伸出端最上侧，对应对流换热系数为采用曲线加载时，变形峰值为4.096 mm；采用系数为0.02时，变形峰值为3.481mm。

（2）U形板呈“鼓泡”状，左连接板伸出端向x正向收缩变形，两侧板自由边均向内收缩变形。

（3）系数为曲线加载时，应力峰值为448.1 MPa；系数为0.02时，峰值为452.1 MPa。不同对流散热系数对残余应力峰值影响很小。

（4）系数为曲线加载时，变形误差为34.3%；系数为0.02时，误差为17.1%；应力分布与对流换热系数为0.02时趋势一致，误差为32.6%；采用曲线加载，不考虑低应力区结果，误差为21.1%。满足工程应用要求，证明了模拟结果的准确性。

（5）两种加载方式预测焊接变形均满足要求。应力预测时，在焊缝较多、应力分布复杂的情况下，建议采用曲线加载方式；反之，采用系数为0.02加载。

[1]Ueda Y，Murakawa H，Ma N.Welding deformation and residual stress prevention[M].New York：Elsevier，2012.

[2] Deng D.Influenceofdeposition sequence onwelding residual stress and deformation in an austenitic stainless steel J-groove welded joint[J].Materials and Design，2013，（49）：1022-1033.

[3]周世杰，李云涛，宋继顺，等.激光焊接热源和焊速对温度场影响的数值模拟[J].电焊机，2014，44（10）：85-88.

[4]王学东，何恩光，陈俐.拘束条件对薄板T形接头双光束激光焊接变形的影响[J].焊接学报，2016，37（3）：101-105.

[5]房元斌，王勇，王灿，等.高强钢Q890中厚板残余应力测量技术研究[J].电焊机，2016，46（10）：85-89.

[6]Goldak J.Modeling thermalstressesanddistortionsinwelds [M].ASM International，1990：71-82.

[7]张文钺.焊接传热学[M].北京：机械工业出版社，1989.

[8]侯志刚.薄板结构焊接变形的预测与控制[D].湖北：华中科技大学，2005.

[9]张超.基于强化散热的焊接变形预测与控制[D].山东：中国海洋大学，2012.

Page 26设计时要重点考虑变幅机构，使其激励频率远离塔机的固有频率。总结各阶振型可知，基于桁架模型的塔机起重臂结构为一低频振动系统，各阶固有频率均较低且相差不大，在使用过程中要注意避免塔机吊绳的摆动和载荷的施加与释放等低频源激扰，防止发生共振。

在保证塔式起重机的静强度和稳定性的基础上，综合各种不同工况下的最大应力变化趋势及其振动特性分析，重点监测应力幅较大处，同时设计塔机时增加型材截面尺寸，而在应力幅较小的地方则可适当减小型材截面尺寸。本研究可以方便地获得塔机受到的最大、最小应力和结构变形情况，从而找出其危险点，为塔机安全监测提供理论支持，同时为塔机进一步优化设计提供理论依据。

参考文献：

[1]曾攀.有限元分析及其应用[M].北京：清华大学出版社，2004.

[2]赵腾龙，姚新军.ABAQUS6.6在机械工程中的应用[M].北京：中国水利水电出版社，2007.

[3]姚克恒，殷晨波.以ANSYS为平台的塔式起重机臂架有限元分析与关键技术研究[J].现代制造工程，2009（12）：47-51．

[4]李然，陈栋梁，姜冰.塔式起重机静态及模态安全性分析[J].起重运输机械，2012（9）：68-70.

[5]王纲居，穆铭豪，孙远韬.塔式起重机金属结构模态分析及其实验测试修正[J].中国工程机械学报，2013（8）：354-358．

[6]GB/T 13752-1992，塔式起重机设计规范[S].北京：中国标准出版社，1993．

[7] Ju Feng，Choo Yoo Sang.Dynamic analysis of tower cranes [J].American Society of Civil Engineers，2005，131（1）：88-96.

[8]师汉民.机械振动系统—分析·测试·建模·对策（上册）（第二版）[M].武汉：华中科技大学出版社，2004.

Influence of convective heat transfer coefficient on welding deformation and stress of screed

ZHANG Huaqing1，FANG Yuanbin2，WANG Weiwei3
（1.XCMG Road Machinery Corporation，Xuzhou 221004，China；2.Jiangsu Xuzhou Engineering Machinery Research Institute，Xuzhou 221004，China；3.XCMG Xuzhou Hydraulics Co.，Ltd.，Xuzhou 221004，China）

The finite element is used to simulate postwelding deformation and stress distribution of screed with different convection heat transfer coefficients.And the results are verified by using feeler gauges and x ray method.The results show that overall deformation trend is bubble shape of U-shaped plate，and the extended end of the left connecting plate shrinks and deforms along the forward direction of x axis. And the free edges of two side panels are concave.The maximum deformation position appears on the tip of the connecting plate extended end.When the convective heat transfer coefficient loads temperature change curve，the deformation error is 34.3%.When the coefficient is 0.02，the error is 17.1%.Different coefficients have little effect on the peak values of the residual stress.The trend of stress distribution is consistent with that when the convective heat transfer coefficient of 0.02 and the error is 32.6%.Using curve loading and without considering low stress zones，error is 21.1%.All of them meet the requirements of engineering application，which proves that accuracy of the simulation results.Two loading modes can predict welding deformation.Under the circumstance of many welds and complicated stress distribution，the curve loading method is recommend，otherwise the loading method with coefficient of 0.02 are recommend.

convective heat transfer coefficient；finite element；welding deformation；stress

TG404

A

1001－2303（2017）05－0027-05

10.7512/j.issn.1001-2303.2017.05.06

2016-11-18

张华清（1977—），男，工程师，硕士，主要从事焊接工艺技术研究工作。E-mail：xcmgzhang@139.com。

本文参考文献引用格式：张华清，房元斌，王伟伟.对流换热系数对熨平板焊接变形和应力的影响[J].电焊机，2017，47（05）：27-31.