基本不等式为例谈数学中的题型归纳

广东省中山市小榄中学(528415) 刘晓聪

基本不等式为例谈数学中的题型归纳

广东省中山市小榄中学(528415) 刘晓聪

日本教育家铃木镇一在他的教育理论中强调“重复,重复,再重复”,通过反复训练让学生形成条件反射.这样的方法优点是简单,缺点是效率偏低,而且容易遗忘.铃木镇一还强调记忆训练,他说“记忆是一种极为宝贵的东西,有了记忆作基础,才有体验,才有推理.”记忆高手们虽然在记忆方法上各有不同,但共同点是将零散的记忆内容用特有的规律或方法串联起来.在数学学习中对某一知识点的归纳总结,可以帮助我们更好地记忆和运用,并且归纳总结最好是能由学生独立完成.这就好比家里的东西如果是自己动手分类整理的,就可以很快地找出自己想要的东西;但如果是其他人整理的,尽管很有条理,也不一定能很快找到自己想要的东西.下面我们准备好一些抽届,自已动手给它们贴上标签,然后将我们遇到的题目逐一装进去.

下面以“基本不等式”这一节内容为例说明如何对常见题型归纳总结.课本必修5基本不等式一节中有这样一个例题.

例1:(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长,宽各为多少时,所用篱笆最短,最短的篱笆是多少?

(2)一段长为36m2的篱笆围成一个矩形菜园,问这个矩形的长,宽各为多少时,菜园的面积最大,最大面积是多少?

分析:设矩形菜园的长为x m,宽为y m,(1)xy=100,求2(x+y)的最值,(2)中2(x+y)=36,x+y=18,求xy的最值.

这是基本不等式的两种常见题型,可就由此归纳为两种题型.

题型一、求和的最值,乘积为定值.

题型二、求乘积的最值,和为定值.

在近一步的练习中很快我们就发现不同于以上两种类型的题目.

题型三:和为定值,求和的最值.

分析: 如果按照题型一、二的观察方式,例2可看作是和是定值,求和的最值.很明显不能直接使用基本不等式,需要另辟新径.

解略.

题型四:变条件等式为不等式求最值.

例3:(2013浙江文)若实数x,y满足x2+y2+xy=1,则x+y的最大值是___.

分析:本题中,条件是和,结论也是和,但条件与结论没有倒数关系,显然不具备使用题型三方法的条件.

解略.

注:将条件中的等式运用基本不等式变为不等式,通过解不等式来找最值.

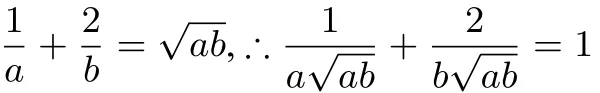
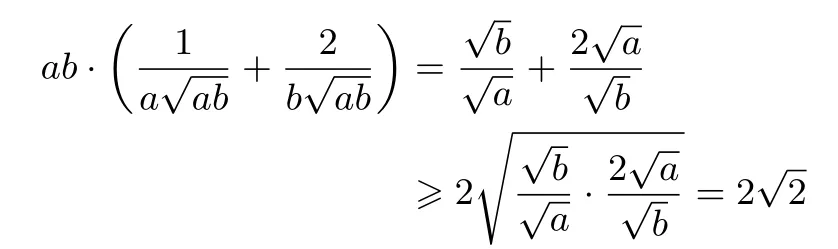
虽然,这里的解法和题型三有一定出入,不是求和的最值,但方法本身与题型三的解法是一致的.因此,我们可以将这种解法归纳到题型三.

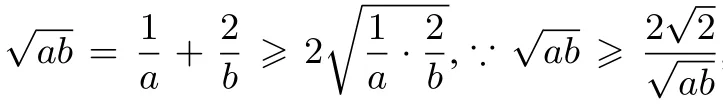
在本章的所有练习结束后,基本不等式这一节共总结出以上四种题型.这里的总结不一定要全面,关键是需要学生在做题时自行去归纳训练.这样反复的归类,记忆会比较牢固,能很好地解决学生临场忘题的毛病.特别对基础一般的学生,也能体会到多题一解,一题多解的乐趣,提升学习数学的兴趣.