多维思考引领教学 生态互动激活课堂——以一道高考试题的教学运用为例

安徽省滁州中学(239000) 郭守静 张晓建

多维思考引领教学 生态互动激活课堂
——以一道高考试题的教学运用为例

安徽省滁州中学(239000) 郭守静 张晓建

2016年4月,笔者所在滁州市郭守静中学数学名师工作室开展了高三数学复习课中生态课堂的构建研讨会,并上了一节关于数列的专题复习课.本节课的设计理念与想法是“多维思考引领教学,生态互动激活课堂”.在设计过程中,笔者以2014年安徽省高考数学理科试题第21题为教学内容,引导学生“多维思考”,开展“生态互动”的教学活动.

真题再现(2014年安徽省高考数学理科第21题)设实数c＞0,整数p＞1,n∈N∗.

(1)证明:当x＞−1且x/=0时,(1+x)p＞1+px;

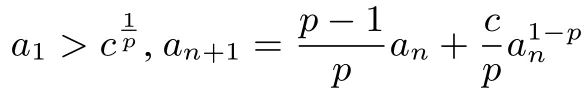
本题的第一小问实际上选自《普通高中课程标准实验教科书数学选修4-5不等式选讲》第四章第二节《用数学归纳法证明不等式》的例3,也即贝努利不等式.高考试题的命制来源于课本的例题,这也要求我们在高三复习中应回归课本,逐本朔源.在教学过程中,我设计了问题串,促进学生学会合乎逻辑的思考,促使学生自然生成解题思路,多维度的分析问题,达到生态互动,激活课堂.

问题1 此不等式的证明如果把p看作变量,那么就是一个关于正整数的不等式,你能想到用什么方法证明呢?我们常用什么方法证明关于正整数的不等式呢?

学生1 数学归纳法,并顺利完成证明.

解法1 (数学归纳法)

(1)当p=2时,由x/=0得(1+x)2=1+2x+x2＞1+2x,不等式成立

(2)假设当p=k(k≥2)时不等式成立,即有(1+x)k＞1+kx.当p=k+1时,(1+x)k+1=(1+x)(1+x)k＞(1+x)(1+kx)=1+x+kx+kx2＞1+(k+1)x所以当p=k+1时不等式成立.由(1)(2)可知,不等式成立.

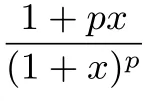
问题3 问题即转化为证明an＜1,那我们需要解决数列{an}什么方面的性质呢?学生经过思考得到需要研究{an}的单调性,由学生完成并展示解法2.

评析: 此处的设计目的和意图是通过问题驱动带动学生去复习巩固知识,通过解决数列与不等式的基本方法数学归纳法和数列的单调性来解决问题,起到复习基本知识和基本技能的作用.

问题4 我们用数列的思想解决了本题,那么现在我们观察发现(1+x)p(p＞1,p∈N∗),这样的结构我们同学能够想到你所学过的什么知识呢?

学生2:二项式定理

教师: 我们可不可以用二项式定理来证明这个不等式呢?由二项式定理可得:(1+x)p=1+px+C2px2+···+Cppxp.

教师:是否可以直接得到(1+x)p=1+px+C2px2+ ···+Cppxp＞1+px?

学生3: 不行,因为x的范围有影响,可以考虑对分x＞0和−1＜x＜0两种情况讨论.学生考虑的非常好,由此给出下列解法.

解法3:当x＞0时,用二项式定理来证明(1+x)p= 1+px+C2px2+···+xp＞1+px.

教师:当−1＜x＜0时,怎么办?

学生3:好像不能判断符号,要不也用数学归纳法证明? (学生发现了问题,但没有找到解决的办法,于是又借助前面所学习的方法来解决这种情况)

问题5 当−1＜x＜0,我们是可以用数学归纳法来补充证明,除了数学归纳法之外还有没有其他的办法?我们是把p看作变量,来解决问题的,是否可以把x看作变量来研究呢?如果把看作变量,则是一道函数与不等式的问题,我们用什么方法?(这里引导学生突破思维的障碍,变换角度,试图通过函数与导数的思想方法来解决本题)

学生4:导数

教师: 很好,那同学们思考一下,应该构造怎么样的函数呢?

学生4:解法4:构造函数,记f(x)=(1+x)p−px−1(x＞ −1),则f′(x)=p(1+x)p-1−p(x＞ −1)结合导数可得函数f(x)在(−1,0)上单减,在(0,+∞)上单增故f(x)在x=0处取得极小值即最小值f(0)=0,所以f(x)=(1+x)p−px−1≥0.又x＞−1且x/=0所以f(x)=(1+x)p−px−1＞0,原不等式成立.

学生3:解法3中,当−1＜x＜0时,也可以用导数解决.

评析: 此处的设计目的和意图是引导学生变换思考的角度,转变变量,运用函数的思想来解决关于数列和不等式的问题,我们需要借助导数研究函数的单调性,求出最值,进而证明不等式.

教师:非常好,同学们已经从数列的角度以及函数与导数的角度解决的问题,老师在这里还有其他的方法,同学们想不想知道?(学生很是惊奇,还有方法?)

现在我回归本身,第一问实际上也是一个不等式证明,那我们可不可以用不等式的方法来解决问题呢?

给出引理1:xn−yn=(x−y)[xn-1+xn-2y+···+ xyn-2+yn-1]

教师:同学们可不可以结合上述等式对问题进行分解? (学生都跃跃欲试)

学生5:由xn−yn=(x−y)[xn-1+xn-2y+···+ xyn-2+yn-1],∴(1+x)p−1p=x[(1+x)p-1+(1+x)p-2+ ···+1]

教师:很好,请同学完成解答.

解法5结合xn−yn=(x−y)[xn-1+xn-2y+···+ xyn-2+yn-1]∴(1+x)p−1p=x[(1+x)p-1+(1+x)p-2+ ···+1].

当 x＞ 0时,(1+x)k≥ 1(k=0,1,···,p−1)∴x[(1+x)p-1+(1+x)p-2+···+1]＞px(p≥2)∴(1+x)p−1＞px=⇒(1+x)p＞1+px.

当−1＜x＜0时有0＜(1+x)k＜1,∴(1+x)p-1+ (1+x)p-2+···+1＜p,∴x[(1+x)p-1+(1+x)p-2+···+1]＞px=⇒(1+x)p＞1+px.

教师: 我还有个方法,大家想不想知道?(此时的课堂,学生已经完全投入到思考问题,解决问题中,按照我所设计的问题串,学生思维活跃,积极思考)教师给出证明方法:

评析:不等式的解决方法技巧性较强,教师在这里不是让学生直接去用,二是给出引理,引导学生去试图解决问题,在提醒的同时,也调动了学生学习的积极性,在引导学生使用什么方法来解决问题的前提下,可以克服学生做题的盲目性.但由于技巧性太强,且超越了考试大纲,故在课堂教学中,教师最终展示了解答.

多维思考引领教学,不仅能是学习者学会学习,促进学生思维的多元化发展,同时也为学习者学会终身学习打下了夯实的基础.而以生态互动激活课堂的真实意义在于让学生不再把学习看作是一件痛苦的事情,他们是课堂的主人,他们享受着学习所带来的快乐,并同时乐于和别人去分享所学,在活动中学习,在问题中学习,透过问题,感悟数学的真谛.

有效就看问题是否发展了学生的数学概括能力,案例2和案例1最大的区别在于学生根据自己的经历,初步而又基本准确的给出偶函数的定义,也就是抽象出了数学概念,当数学概念被学生准确抽象并合理表达出来后,学生就能更好地理解概念、命题、方法和体系,就能通过概念去认识、理解、把握事物的数学本质,而这时“数学抽象”素养在“概念教学”中就自然而然的“落地生根”了,数学概括的过程也就是数学能力、数学素养的形成过程,这不仅体现在《函数的奇偶性》的概念教学.