新课标下初中数学思想方法的渗透——基于函数与方程“融合”的探究

广州市铁一中学(510600) 言彦

新课标下初中数学思想方法的渗透
——基于函数与方程“融合”的探究

广州市铁一中学(510600) 言彦

目前,在初中数学学习中,很多学生遇到综合性题目就觉得困难重重,听老师的讲解觉得容易理解,换个情境时又觉得无从下笔,数学素养不能得到较大的提高,究其原因,笔者认为是数学思想方法在教学中渗透不足所造成.数学基本思想方法正如新课程标准(2011年版)指出的那样”是需要学生经历较长的认识过程,逐步理解和掌握的”,教师应当在进行数学知识教学的同时,有意识地渗透数学思想方法.而很多教师只是在进行课堂小结时,才提到用过的数学思想方法的名称,并没有在整个学习过程中进行渗透,导致学生头脑中的数学思想方法不够具体,对数学思想方法的理解不够透彻,难以在后续的学习中灵活运用.笔者针对这一问题进行研究,通过将函数与方程内容进行“融合”,并在“融合”的教学过程中不断渗透各种思想方法,最后达到提高学生综合素质与能力的目的.

一、在“融合”中渗透数学思想方法的原理

1.函数知识与方程知识联系密切是“融合”的基础

函数是中学数学的”基石”,函数与方程的知识内容贯穿于初中数学大部分教学内容,几乎渗透到初中数学的各个领域.虽然函数和方程是两个不同的概念,但是这两种数学知识却有着密切的联系,如:一次函数可以看成是一个二元一次方程、一元二次方程根的个数就是二次函数的图象与x轴交点的个数等等,这种紧密的关系,为函数知识与方程知识在初中数学中的相互转化提供了条件,为两者的“融合”提供了基础.

2.函数与方程思想和其他思想方法联系密切是渗透的条件

函数与方程的理论内容蕴含着诸多数学思想方法.在函数与方程的学习过程中自然能够渗透函数思想和方程思想;函数与方程思想蕴含了函数、方程、不等式间的相互转化,在此基础上通过比较和抽象,形成数学化归思想.利用函数可以表示数学问题中的数量关系和变化规律,使问题得以解决,这个过程与模型思想密切联系;而利用平面直角坐标系,函数可以将代数与几何问题有机结合,无论是利用几何直观分析函数问题或利用函数思想解决几何问题,都体现了数形结合思想和化归思想.所以函数与方程思想和其他思想方法联系密切,为渗透数学思想方法的教学提供了有利的条件.

3.“融合”是渗透的手段

张景中院士用面积法“一线串通”几何内容的教学方式获得了成功,函数是中学数学的“基石”,函数与方程的知识内容也贯穿于初中数学大部分教学内容,几乎渗透到初中数学的各个领域,这为函数与方程的“融合”提供了基础.

钱佩玲教授指出:“数学思想方法是隐形的本质的知识内容,因此在教学中教师必须深入钻研教材,充分挖掘教材中有关的思想方法”.所以在教学过程中将函数与方程模块“融合”,不仅是按新课标的要求“用好教材”,更是将“无形的”数学思想方法更自然地渗透在“有形的”数学知识内容中.

二、在“融合”中渗透数学思想方法的方法

新课程标准提到:数学思想蕴涵在数学知识形成、发展和应用的过程中,所以数学基础知识与思想方法是密不可分的,教学的过程中应当紧密结合这两条线,通过函数与方程“融合”的方法,在“融合”的过程中精心设计数学活动,在知识的形成过程中有意突出数学思想方法的核心问题,在知识的应用过程中将对思想方法的思维示范与引导学生体验、感悟数学思想方法相结合,在知识应用后总结认知操作程序,是渗透数学思想方法的有效策略.

1.在“融合”中渗透转化思想

转化思想的内涵就是将未知的难题转化成已学的问题,将抽象的表述转化为具体的描述.函数与方程联系密切,在学习方程知识时,可以融合函数知识,从而渗透转化思想.又因为在概念、公式形成过程中实施局部探究,是渗透数学思想方法的基本方法,所以在学习方程的概念时,通过设计适当的问题情境融合函数知识,对渗透转化思想尤其有效.例如学习方程的概念时利用函数引入:

问题:

(1)一台计算机已使用1700h,预计每月再使用150h,请写出经过t月这台计算机的总使用时间y与月数t的函数关系式?当使用时间2450h时,你能得到什么等式?

(2)长方形的面积为1,设长为x,宽为y,则y与x的关系如何?当y=0.5时,你能得到什么等式?

(3)一个正方形的边长为x,面积为y,则y与x有什么关系?当y=0时,你能得到什么等式?观察上面的等式,它们有什么共同特征?这些都是含有未知数的等式——方程(equation).

思考:函数与方程有什么关系?

当函数取定一个值时,函数解析式转变为一个方程.

设正方形的边长为(x−1)cm,周长为ycm,则y与x有什么关系?是什么函数?当y=10时,你能得到什么样的等式?当y=24,y=30,又如何呢?

这些等式有什么共同点?你能给他们起个名字吗?

在学习二元一次方程的概念时,可以再次引导学生观察二元一次方程和一次函数解析式,引导学生发现一次函数也可以看成二元一次方程.同样在学习分式方程和一元二次方程时,都可以引导学生发现函数与方程之间的转化思想.

这样在方程知识的形成过程中反复“融合”,学生能够对转化思想进行模仿应用和体会,转化思想的渗透效率就更高了.

2.在“融合”中渗透数形结合思想

我们在学习函数时,常常通过二元一次方程组求两条直线的交点等方式渗透以数解形的方法,利用函数图象求解函数的解析式渗透以形解数的方法,但在学习方程的时候对数形结合思想的渗透很少,而方程和函数思想与数形结合思想都有密切联系,所以在讲解方程的问题时可以将函数的问题也融入其中,有意突出渗透数形结合思想,不仅能使学生在知识的应用过程中充分感悟数形结合思想,体验以形解数、以数解形的方法带来的优越性,还能让学生通过探究问题的多角度性进一步理解数形结合思想.

将方程和不等式的教学内容与函数“融合”,能让数形结合思想方法更多地建立在数学实践活动的基础上,从而能让学生在体验的基础上进行数形结合思想方法提炼的关键认知操作.

3.在“融合”中渗透模型思想

模型思想的渗透必须包括具体的数学学习内容,而方程和函数思想都是模型思想的下位思想方法,所以方程和函数都蕴含着模型思想,通过“融合”方程与函数中的实际问题,可以使模型思想渗透更为高效更为透彻.

首先要通过“融合”在模型的形成过程中渗透模型思想,即将模型思想的教学融入方程和函数的基本概念教学.方程和函数的“融合”能帮助学生更好地理解掌握其中的重要概念、性质定理的形成过程和抽象过程,挖掘并体会其中蕴含的模型思想,如通过“融合”的方法学习方程概念的形成过程就充分体现了“等号两边的两件事情是等价的”这一数学建模的本质表现(“融合”方法在前面已说明,在此不再赘述).学生在知道有哪些模型,并理解了这些模型后,才能更好的应用模型解决实际问题.

其次要通过“融合”在模型的应用过程中渗透模型思想,即在问题解决过程中主动联想,在重要概念原理的应用过程中,帮助学生体会运用模型思想的过程.函数模型和方程模型都是把语言表达的问题数量化,抓住问题中的数量关系进行建模,区别在于在运动变化的过程中,函数模型刻画的是两个变量的联系情况,而方程模型刻画的是两个变量的瞬间情况,所以在实际问题中“融合”方程和函数模型,使得模型思想的渗透事半功倍.

4.在教学的各个环节进行“融合”

在方程和函数“融合”过程中还能渗透其他的数学思想方法,但无论渗透哪种数学思想方法,都应该在“融合”时将思想方法目标和教学环节切实对应,设计相关数学活动,给学生增加领悟思维程序的渠道.

值得注意的是,数学思想方法的渗透需要大量的样例,所以不仅要在课堂教学中“融合”,还要在课后练习中“融合”.如在进行二元一次方程与实际问题的教学后,可以设计和函数有关的练习以渗透数形结合思想:甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)的关系如图所示,请根据图象所提供的信息解答下列问题:

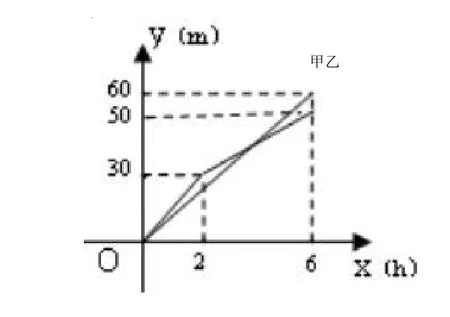
图1

①甲队在0≤x≤6的时段内,y与x之间的函数关系式;

②乙队在2≤x≤6的时段内,y与x之间的函数关系式;

③当x为何值时,甲、乙两队在施工过程中所挖河渠长度相等?

这样学生能通过更多的具体实例进行思辨,感悟到数学思想方法的实质,并内化为思维程序,使学生在数学思想支配下的思维能力逐步增强,在各种情景下都能自如运用各种数学思想方法.

三、在“融合”中渗透数学思想方法的反思

1.能帮助学生加深对数学思想方法的理解

初中学生通常对思想方法仅停留于表面,当与新情境相结合时,部分同学会感到吃力,这是因为学生对数学思想方法的理解比较孤立,没有用相同的思想方法解决不同形式、不同情境问题的经历,没有利用联系的思维来理解数学思想方法,没有在一个更大的空间中认识数学思想方法,所以在具体问题的解决过程中容易陷入困境.通过将函数与方程“融合”来渗透数学思想方法,不仅能在数学思想方法形成的过程增加理解渠道,还能使学生在“融合”中不断巩固对数学思想方法的认识,不断加深对数学思想方法的理解,使学生能有意识地运用数学思想方法解决问题,从而增强迁移能力.

2.能帮助学生构建数学思想方法网络

数学思想方法网络是通过横向联系和纵向概括活动来逐步建构的.通过“融合”可以对不同思想方法进行纵向概括,如:从函数概念到二元一次方程概念可以渗透转化思想等.通过“融合”还可以建立不同思想方法上的横向联系.利用方程和函数之间的联系,可以将多种思想方法进行类比、交叉、融合,如让学生掌握方程、函数等模型思想方法后,在此基础上通过比较和抽象,形成数学化归思想.这样,将学生头脑中的化归思想具体化,有助于产生更深刻的感悟.通过不断地进行横向比较和纵向概括,不断具体化并拓展已有的思想方法,可以帮助学生构建数学思想方法网络,使得数学思想方法的渗透更具有系统性.

3.能帮助学生提高数学素养

著名教育学家布鲁纳在《教育过程》中指出:对基本数学思想方法的融会贯通能够使得知识的迁移更加容易.所以通过方程和函数“融合”的方法帮助学生构建数学思想方法网络后,不仅能提高学生对数学知识的运用能力和概括能力,还能让学生在提高成绩的同时树立科学的思维方式,从而形成正确的数学观,真正提高数学素养.

综上所述,通过函数与方程“融合”来渗透数学思想方法,提高了数学思想方法渗透的有效性,事半功倍.