一种加权的分块邻域保持嵌入人脸识别算法∗

一种加权的分块邻域保持嵌入人脸识别算法∗

陈斌1李康顺2王宇川3

（1.广东建设职业技术学院现代教育技术中心广州510440）（2.华南农业大学数学与信息学院广州510640）（3.广州现代信息工程职业技术学院广州510633）

在人脸识别中，传统的子空间识别算法将整幅人脸图像作为输入模式。但是，当人脸图像的光照、姿态和表情变化较大时，仅考虑图像的全局特征，识别的效果不够理想。为此，论文提出一种加权的分块邻域保持嵌入人脸识别算法。算法先对人脸图像进行分块，对分块得到的子图像利用邻域保持嵌入算法分别提取特征信息，并利用Geman-McClure函数和类标信息计算各分块子图像的权重。该算法能够增强分类效果，对表情、光照、姿势等变化具有鲁棒性，在ORL和Yale人脸数据库上对论文的提出的算法进行了验证。

人脸识别；邻域保持嵌入；加权分块

Class NumberTP391.4

1 引言

人脸识别是一种重要的生物特征识别技术，在身份认证、视觉监控以及人机接口等方面具有广阔的应用价值。近年来，基于子空间的人脸识别算法得到广泛关注。子空间分析的出发点是根据一定的性能目标，将高维的人脸图像特征通过空间变换投影到低维子空间中去，从而压缩原始数据维数，为数据的描述提供方便，并降低计算的复杂度。其中，主成分分析（PCA）［1］和线性判别分析（LDA）［2］是两种常用的子空间分析方法。但是，这两种方法只能发现数据的欧几里得结构，而不能发现高维数据的内在分布规律。基于此，非线性流形学习算法被提出：等距映射（ISOMAP）［3］、局部线性嵌入（LLE）［4］、拉普拉斯特征映射（LE）［5］。由于流行学习方法缺乏明晰的投影矩阵从而对新数据难以处理。因此，LLE的线性近似算法——邻域保持嵌入算法（NPE）［6］被提出，它能有效地保持原始数据的局部特征和处理新数据点。

在人脸识别中，传统的子空间识别算法将整幅人脸图像作为输入模式。但是，当人脸图像的光照、姿态和表情变化较大时，仅考虑图像的全局特征，识别的效果不够理想。为此，基于分块特征的算法被提出［7～10］。分块PCA算法（SpPCA）［7］，先对人脸图像集进行分块，进而对划分后的各子图像集使用PCA算法进行特征提取。加权分块PCA算法（Aw-SpPCA）［8］，通过计算各分块图像的探测集和原型集的相似度确定各子图像的权重。

基于分块加权的思想，为增加分类效果，本文提出了一种加权分块邻域保持嵌入算法（NPE），简称Aw-SpNPE算法。算法考虑了类标信息和距离分布对子图像的权重的影响，计算方法简单方便，对姿势、光照和表情等变化有较好的鲁棒性。在ORL和Yale人脸库中的对比实验证明了提出的加权方法的有效性。

2 邻域保持嵌入算法（NPE）

设在高维欧氏空间RD中有样本集X=[x1,x2,…,xN]，近邻保持嵌入算法（NPE）［6］寻求一个投影矩阵A，希望将这些样本映射到一个相对低维的特征空间Rd(d＜＜D)。这样，样本在新特征空间中的表示为Y=ATX。NPE主要包括以下三个步骤：

1）选择近邻点，构造近邻图G。近邻点选择方案为：①无监督方案，根据k近邻或者ε邻域计算样本点的近邻点集；②有监督方案，从同类样本中选择近邻点集。本文采用无监督方案。

2）计算近邻重建权重矩阵W。令xij（j=1,2,…,k）表示xi的k个近邻点，wij表示xi与xj之间的权值。若xj不是xi的近邻点，则wij=0。NPE假设每个局部近邻是线性的。所以，每个数据点xi可以通过它的k个最近邻点重构，重构的损失函数函数为

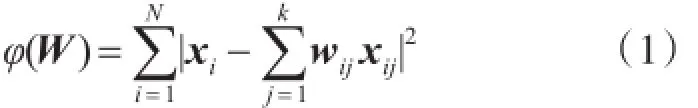
3）计算投影向量A。NPE认为：如果wij能在RD空间里重构数据点xi，则它也可以在Rd空间中重构对应的点yi。因此，嵌入映射变化矩阵A通过求解下面最小化问题得到：

其中，M=(I-W)(I-W)T，约束条件ATXXTA=I。事实上，通过简单的运算，式（2）的最优化问题可以转化成下面的广义特征值求解问题，即

投影向量A=[α1,α2,…,αd]是由(XXT)-1XMXT的前d个最小非零特征值所对应的特征向量构成。由于XXT可能是奇异矩阵，一般通过对X利用PCA变换来保证XXT是非奇异的。

3 分块加权的邻域保持嵌入算法

3.1人脸图像的分割

设人脸数据库有N张训练图像。每幅图像被分割成K份相等大小且不重叠的子图像，并将相同行、相同列的子图像放在一起构成子图像集，从而得到K个分离的子图像集，图像的分割过程如图1所示［7～10］。

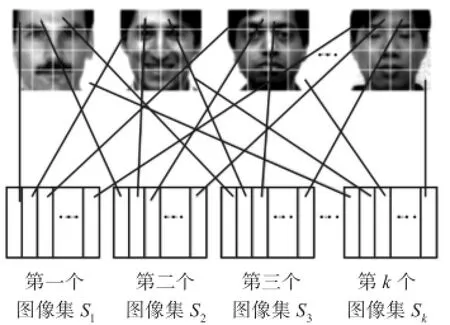
图1 图像分割的过程

3.2对子图像集进行NPE降维算法

设Sl(l=1,2,…,K)表示第l个子图像集，Xl=[xl1,xl2,…xlN]表示子图像集Sl里面的N个列向量，其中xli表示第i个样本的第l个子块。对各子图像集Sl使用NPE降维算法进行降维，并最后得到投影矩阵Al：

式（4）的d个最小的非零特征值所对应的特征向量构成投影矩阵Al=[αl1,αl2,…,αld]。

3.3各子图像集权重的计算

令Ω(xli,k)表示样本xli的k近邻样本构成的集合，Θ(xli,k)表示样本xli的k近邻中与xli类标相同的样本构成的集合，xlj(j=1,2,…,k)表示样本xli的k个近邻点。影响类间区分能力的关键因素之一为样本xlj(j=1,2,…,k)和样本xli的类标是否相同。基于以上的考虑，认为所有k近邻样本数中，和样本xli的类标相同的数目占比大的子图像应该获得较大权重。进一步，采用Geman-Mc⁃Clure函数来衡量k近邻样本对xli的影响：

Elij用来度量第j个样本对第i个样本的影响程度，距离越近，影响程度越大。‖xli－xlj‖*为标准化处理后的距离，满足0≤‖xli－xlj‖*≤1，σ为控制系数，本文选取σ=1进行实验。令SEli表示第l个子图像集中第i个样本xli的k近邻样本对xli的识别效果产生的总影响，即其中，Ω(xli,k)表示样本xli的k近邻中样本构成的集合。NEli表示第l个子图像集第i个样本xli的k近邻点中和xli类标相同的样本对xli的识别效果产生的总影响，即，其中，Θ(xli,k)表示样本xli的k近邻中与xli类标相同的样本构成的集合。显然，NEli越大的子图像赋予的权重应该越大。最后，第个子图像集的权重的计算公式如下：

3.4分类

对一张未知的人脸图像x，先将人脸分割成K张子图象，采用分类器投票的方式进行分类。通过这种方式，光照变化、部分遮挡等局部变化，将被限制在几个局部的子图像那里，从而增强识别人脸的鲁棒性［8，10］。令表示人脸图像属于第e类样本的概率。其中，ωl为第l个子图像集的权重。如果第l个子图像属于第e类，=1，否则=0。最终的分类结果为

4 实验结果及分析

我们比较了SpPCA［7］、Aw-SpPCA［8］、SpNPE、Aw-SpNPE、Aw-SpPCA1等算法在ORL和Yale人脸库的识别性能。其中，SpNPE是平均加权的分块NPE算法，Aw-SpPCA1、Aw-SpNPE是本文提出的加权方法分别与SpPCA与SpNPE相结合的算法。

4.1ORL人脸库

ORL人脸库包含40个人的正面图像，每人10幅图像，图像倾斜变化和旋转变化在20%左右，尺度变化在10%左右，图像分辨率大小为112×92像素。为了简化运算、提高运行速度，将图像裁剪成大小48×48。图2为ORL人脸数据库中某人的人脸图像。

图2 ORL人脸数据库中某人的人脸图像

在ORL人脸库中随机选取每个人6幅图像用于训练，其余用于测试。实验中，人脸图像分割成8×8大小子块，最近邻样本数k=5。为了防止随机抽取产生的识别结果偏差，进行重复实验10次，最终取多次实验的均值作为各算法最终的识别率，实验结果如图3所示。Aw-SpNPE算法的识别率比SpNPE提高1.12%，说明了提出的权函数能增强分类效果。

图3 ORL人脸数据库识别率对比

4.2Yale人脸库

Yale人脸库包括15个人，每人11幅，图像中面部表情、细节、尺度、以及光照都有不同程度的变化，图像大小为320×243。实验中将图像裁剪成100×100。图4为Yale人脸数据库中某人的人脸图像。

图4 Yale人脸数据库中某人的人脸图像

在Yale人脸库中随机选取每个人7幅图像进行训练，其余用来测试。实验中，图像分割成20× 20大小子块，最近邻样本数k=5。为了防止随机抽取产生的识别结果偏差，进行重复实验10次，取多次实验的均值作为算法最终的识别率。从表1可以看出，本文提出的Aw-SpNPE算法的识别率比SpPCA、Aw-SpPCA、SpNPE分别提高8.33%、7.67%、1.83%。这说明了提出的方法对姿势、表情和光照等因素变化具有较好的鲁棒性，能够增强分类效果。而Aw-SpPCA1（本文提出的加权方法与spPCA结合）的识别率分别比SpPCA、Aw-SpPCA提高1.33%、0.67%。说明本文提出的分块加权方法对PCA仍然有效。

表1 Yale数据库上不同算法识别率（%）

5 结语

本文提出了一种加权的分块特征邻域保持嵌入算法，考虑了类标信息和距离分布对子图像的权重的影响，计算方法简单方便，对姿势、光照和表情等变化有较好的鲁棒性。在ORL和Yale人脸库中的对比实验证明了提出的加权方法的有效性。同时，可以将本文提出的加权方法应用于其他分块降维方法，诸如SpPCA等。

［1］Kong Hui，Wang Lei，Teoh Eam Khwang，et al.General⁃ized 2D principal component analysis for face image repre⁃sentation and recognition［J］.Neural Networks，2005，18（5）：585-594.

［2］Li Ming，Yuan Baozong.2D-LDA：A statistical linear dis⁃criminant analysis for image matrix［J］.Pattern Recogni⁃tion Letters，2005，26（5）：527-532.

［3］Joshua B.Tenenbaum，Vin de Silva，John C.Langford.A global geometric framework for nonlinear dimensionality reduction［J］.Science，2000，290（5500）：2319-2323.

［4］Sam T.Roweis，Lawrence K.Saul.Nonlinear dimensionali⁃ty reduction by locally linear embedding［J］.Science，2000，290（5500）：2323-2326.

［5］M.Belkin，P.Niyogi.Laplacian eigenmaps for dimension⁃ality reduction and data representation［J］.Neural Compu⁃tation，2003，15（6）：1373-1396.

［6］Xiaofei He，Deng Cai，Shuicheng Yan，Hong-Jiang Zhang.“Neighborhood Preserving Embedding”，Tenth IEEE In⁃ternational Conference on Computer Vision［C］//Washing⁃ton，America，2005：1208-1213.

［7］Chen Songcan，Zhu Yulian.Subpattern-based principle component analysis［J］.Pattern Recognition，2004，37（5）：1081-1083.

［8］Tan Keren，Chen Songcan.Adaptively weighted sub-pat⁃tern PCA for face recognition［J］.Neurocomputing，2005，64（3）：505-511.

［9］Nanni Loris，Maio Dario.Weighted sub-gabor for face rec⁃ognition［J］.Pattern Recognition Letters，2007，28（4）：487-492.

［10］Xue Hui，Zhu Yulian，Chen songcan，Local ridge re⁃gression for face recognition［J］.Neurocomputing，2009，7（4-6）：1342-1346.

A Weighted Sub-pattern Neighborhood Preserving Embedding Algorithm for Face Recognition

CHEN Bin1LI Kangshun2WANG Yuchuan3
（1.Modern Education Technical Center，Guangdong Construction Polytechnic，Guangzhou510440）（2.School of Mathematics and Information，South China Agricultural University，Guangzhou510640）（3.Guangzhou Modern Information Engineering College，Guangzhou510633）

In face recognition，the whole facial image is considered as the input mode in the traditional subspace recognition al⁃gorithm.However，under the circumstances of big changes in illuminations，poses and expressions in facial images，facial recogni⁃tion effects are not satisfactory if only the global features of images are considered.In this paper，a weighted sub-pattern neighbor⁃hood preserving embedding algorithm is proposed for face recognition.Firstly，the original whole face pattern is partitioned into a set of equally-sized non-overlapped sub-patterns.Then，the neighborhood preserving embedding algorithm is directly performed on each sub-pattern to extract its features.And the weight of each sub-pattern is calculated with the Geman-McClure function com⁃bined with the label information.Experimental results on ORL and Yale human face databases showed that the advocated algorithm was more robust for face recognition under the circumstances of big changes in illuminations，poses and expressions in face images.

face recognition，neighborhood preserving embedding，weighted sub-pattern

TP391.4

10.3969/j.issn.1672-9722.2017.05.037

2016年11月7日，

2016年12月29日

广东省科学技术厅科技计划项（编号：2015A030401107）资助。

陈斌，男，硕士，工程师，研究方向：计算机网络与通信、图像处理。李康顺，男，博士，教授，博士生导师，研究方向：演化技术、图像视觉。王宇川，男，硕士，教授，研究方向：计算机技术与应用。