量子衍生萤火虫搜索算法∗

量子衍生萤火虫搜索算法∗

刘显德于瑞芳李滨旭赵思远李盼池

（东北石油大学计算机与信息技术学院大庆163318）

为提高萤火虫搜索算法的寻优能力，通过在经典萤火虫搜索算法中引入量子计算机制，提出了一种量子衍生萤火虫搜索算法。该算法采用量子比特编码个体，采用泡利矩阵确定旋转轴，采用传统萤火虫飞行原理确定旋转角度，采用量子比特在Bloch球面上的绕轴旋转实现个体更新。标准函数极值优化的实验结果表明，与传统萤火虫搜索算法相比，该算法的搜索能力确有明显提升。

仿生智能优化；群智能优化；萤火虫算法；量子衍生优化；算法设计

Class NumberTP183

1 引言

2008年，英国剑桥大学学者提出了一种新的启发式智能优化算法：萤火虫搜索算法（Firefly Search Algorithm，FA）［1］。它源于对萤火虫群体行为的简化和模拟，是一种高级启发式算法。该算法通过萤火虫个体之间的相互吸引达到寻优的目的，是一种基于群体搜索的随机优化算法，具有概念简单、结构清晰、控制参数少、易于实现等优点。目前对萤火虫算法的理论研究尚处于初级阶段。在算法的改进方面，文献［2］提出了变步长萤火虫算法，改进了标准萤火虫算法在所有迭代步中采用固定步长的缺陷；文献［3］提出了控制参数的自适应改进策略，有效解决了控制参数难以合理确定的问题；文献［4］提出了基于搜索空间对称寻优的改进策略，在一定程度上提升了算法的收敛速度；文献［5］提出了带有邻域搜索策略的改进方法，有效提升了优化解的精度。在与其他算法的融合方面，文献［6～7］分别提出了与模糊集、粗糙集融合的新方法。在算法的应用方面，已分别应用于分类器集成修剪［8］、图像检索［9］、水位波动预报［10］、心脏病预测［11］、支持向量机参数优化［12］、蛋白质网络动态预测［13］等许多不同领域，并取得了良好的优化效果。

尽管目前国内外文献已提出多种有关萤火虫搜索算法性能的改进策略，然而有关量子计算与萤火虫搜索的融合研究尚不多见。本文提出一种新颖的量子衍生萤火虫搜索算法，其编码机制为采用带两个相位参数量子比特编码个体，寻优机制为采用量子比特在Bloch球面上的绕轴旋转模拟萤火虫的搜索行为。采用CEC2013的28个标准测试函数做为优化对象，仿真结果验证了提出算法的优越性。

本文提出一种新颖的基于NEQR描述的量子彩色图像加密方案。首先将彩色图像采用NEQR模型描述，采用24个量子比特描述像素的颜色值，然后采用受控旋转门使颜色比特随机旋转，进而实现量子图像的加密。尽管加密过程较为简单，然而经典计算机上的仿真结果表明，与其他同类算法比较，提出方案的加密效果是较为理想的。

2 萤火虫搜索算法

萤火虫搜索算法的核心思想是萤火虫受大于自身亮度的同伴吸引，进而向着同伴前进，借以提高自身亮度，以期找到最优的空间位置。为便于描述，首先给出不同萤火虫之间相对亮度和吸引度的定义。

定义1相对亮度：萤火虫i对萤火虫j的相对亮度为

式中Ii为萤火虫i的绝对亮度，具体数值等于萤火虫i所处位置的目标函数值，γ为荧光吸收系数，可设为某一常数，rij=||xi-xj||为个体i和j之间的距离。式（1）表明，荧光亮度会随着距离的增加而衰减，这恰好模拟了荧光在空气介质中传输时被吸收的行为。

定义2个体吸引度：个体i对j的吸引度定义为下式

式中β0为最大吸引力，即在光源处（rij=0）萤火虫的吸引力。通常可以取β0=1，γ和rij的含义同上。

在萤火虫i的引力作用下，萤火虫j向着i移动，并更新自身位置，具体更新方法如下式所示

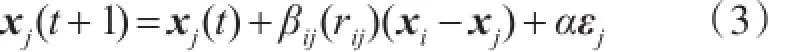
式中t为迭代步数，xi和xj为个体i和j的位置向量，α∈(0, 1)为常数或随迭代步数逐代减小，εj为随机分布的随机数向量，具体可取高斯分布或均匀分布。εj本质上是一种变异行为，以增强种群多样性防止早熟收敛。

3 量子衍生萤火虫搜索算法

本节提出一种量子衍生萤火虫搜索算法（Quantum Inspired Firefly Search Algorithm，QIFA），包括个体的编码机制和搜索机制两部分，下面分别予以介绍。

3.1 QIFA的编码机制

1）基于量子比特的萤火虫位置编码

在QIFA中，萤火虫的空间位置采用基于Bloch球面描述的量子比特编码。设萤火虫数目为N，空间维数为D，记第t代种群为P(t)=[p1(t), p2(t),…, pN(t)]T，则第i个萤火虫位置pi(0)的初始编码可写为

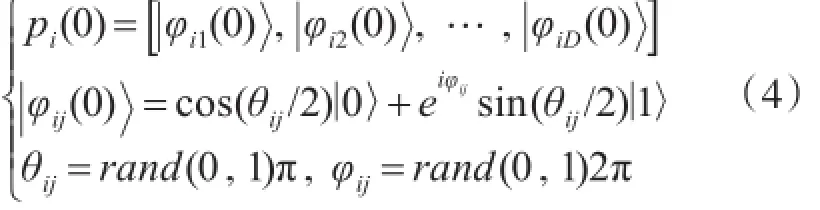
2）量子个体到经典个体的变换

对于采用量子比特编码的萤火虫，只有转换为具体的数值向量才能评价位置（候选解）的优劣，这可以通过对量子萤火虫的投影测量及解空间变换获得。具体方法为首先采用泡利矩阵对量子萤火虫实施投影测量得到其在Bloch球面上的坐标位置，然后通过解空间变换，将这些坐标映射为该萤火虫具体所在的空间位置。泡利矩阵的定义式为

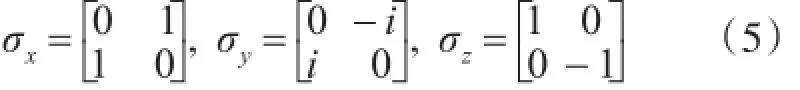
对于第i个萤火虫上的第j个量子比特φij，其投影测量计算式为

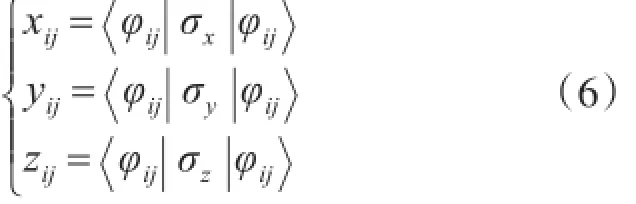
其中i=1, 2,…, N; j=1, 2,…, D。

此时，Xi=[xij]，Yi=[yij]，Zi=[zij]即为萤火虫在Bloch球面上的坐标位置。

3）坐标位置的解空间变换

在QIFA中，每个量子萤火虫都对应到三个坐标位置，然而这三个坐标位置并不是彼此独立的。这是因为三者之间存在++=1的约束关系。因此若一组坐标（例如xij）较优，则另外两组(yij,zij)一般会较差。因此在QIFA中，对于第i个量子萤火虫测量之后得到的三个坐标位置Xi=[xij]，Yi=[yij]，Zi=[zij]，我们只采用Xi=[xij]。

由于xij∈[-1, 1]，因此需要进行解空间变换。记第j维优化空间的取值区间为[Minj,Maxj]，则解空间变换如下式所示。

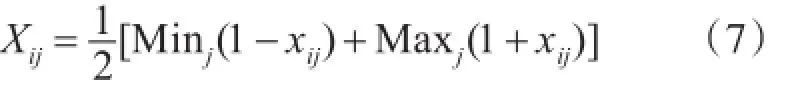
其中i=1, 2,…, N；j=1, 2,…, D。

此时[Xi1, Xi2, ... , XiD]即为第i只萤火虫在寻优空间的实际位置。

3.2QIFA的搜索机制

在QIFA中，搜索机制采用量子比特在Bloch球面上的绕轴旋转实现，其中旋转角度采用式（2）定义的个体吸引度计算，旋转轴采用泡利矩阵决定。具体旋转方法如下。

1）基于量子比特饶轴旋转的位置更新

令φik(t)和φjk(t)分别为第i个萤火虫和第j

个萤火虫中第k个量子比特，在Bloch球面上的对应点分别为Pik=[pikx, piky, pikz]和Pjk=[pjkx, pjky,pjkz]。若个体j优于个体i，则使φik(t)向着φjk(t)移动。根据量子力学原理，量子比特在Bloch球面上的移动可以通过使其绕着某个轴旋转实现。由文献［14］可知，旋转轴可按下式定义：

根据量子计算原理，旋转算子为一个二维酉矩阵，该矩阵由旋转轴、旋转角度共同决定。

在QIFA中，旋转角度采用式（2）定义的个体吸引度计算。令为Pik和Pjk之间的夹角，则φik(t)的旋转角度可按下式设计：

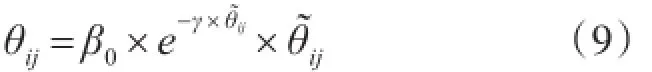
其中β0为控制参数（通常取0.1），γ为常数，通常可取1.0。

至此，当前量子比特φik(t)在Bloch球面上，绕轴Rij转向目标比特φjk(t)的旋转矩阵为

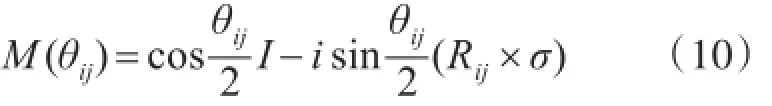
其中I为单位矩阵，σ=[σx, σy, σz]。

φik(t)转向φjk(t)的旋转操作为

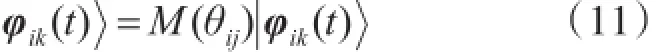
其中t为迭代步数。

在萤火虫i上所有D个量子比特更新之后，进行投影测量、解空间变换、计算目标函数值。

2）基于量子比特随机旋转的局部搜索

在经典萤火虫算法的位置更新式（3）中的最后一项，实际上是也是一种局部搜索策略。在QIFA中，该策略可以用量子比特在Bloch球面上的随机旋转实现。对于每一个萤火虫，首先绕着X轴、Y轴、Z轴之一（具体可随机选择）旋转一个幅度逐代减小的随机角度生成新个体，然后采用贪婪策略更新萤火虫位置。下面给出具体的实现方法。

在Bloch球面上，量子比特绕X轴、Y轴、Z轴旋转δ弧度的旋转矩阵分别为

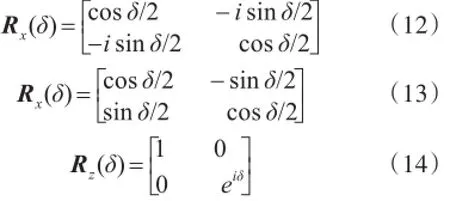
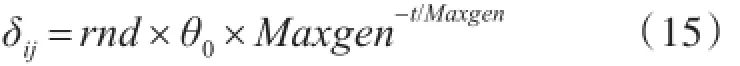
令φij(t)为第i个量子萤火虫中第j个量子比特，首先按下式计算旋转角度：其中Maxgen为限定迭代步数，θ0为转角初值，rnd为区间（0，1）内均匀分布的随机数。

由式（15）可知，显然，δij的幅度随迭代步数逐代减小，这一方面体现了随迭代步数的增加，局部开发能力的增强，同时也与普通FA位置更新式（3）中随机项的作用是一致的。

然后在X轴、Y轴、Z轴之中随机选择一轴Rλ(δ)，λ=X或Y或Z，执行旋转操作其中t为迭代步数。

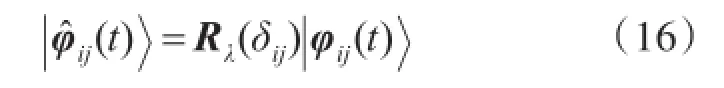
在萤火虫i上所有D个量子比特全部更新之后，进行投影测量、解空间变换、计算目标函数值，最后采用贪婪策略实施萤火虫i的更新。即若φi(t)优于φi(t)则φi(t+1)=φi(t)，否则φi(t+1)=φi(t)。

3.3QIFA的终止条件

关于群智能优化算法的终止条件，通常有多种。例如精度控制：当优化结果达到某一精度阈值，算法终止；误差控制，当优化结果与精确结果的绝对误差小于给定阈值，算法终止；进化速度控制：若连续若干代优化结果无变化，算法终止；步数控制：若寻优步数达到限定步数，算法终止。本文QI⁃FA采用步数控制作为终止条件。

3.4QIFA的实施方案

关于本文提出的QIFA，具体实施方案如下。Step1初始化：种群规模N；空间维数D；限度步数Maxgen；控制参数β0、γ，转角初值θ0，个体初始位置。

Step2计算目标函数值，记录种群最优解，置当前步数t=0。

Step3主循环开始

Step3.1所有个体执行位置更新；

Step3.2所有个体执行局部搜索；

Step3.3更新种群最优解；t=t+1；

若t＞Maxgen，转Step4；

否则转Step3.1。

Step4保存种群最优解，结束。

4 对比实验

4.1测试函数

采用CEC2013定义的28个标准函数［15］作为优化对象，如表1所示。其中（S）表示该函数的变量是可分离的，（N）表示变量是不可分离的，n表示该函数由其他n个基本函数复合而成，所有函数均为极小值优化。

表1 28个CEC'13测试函数简介

4.2对比方案

为体现所提出的QIFA算法的优良性能，所有函数的优化结果将与普通萤火虫搜索算法（FA）［1］、变步长萤火虫算法（Variable Step Size Firefly Algo⁃rithm，VSSFA）［2］，按维对称寻优的萤火虫算法（Op⁃position and Dimensional based FA，ODFA）［4］进行对比。为保证对比结果客观公正，四种算法采用相同的种群规模。考虑到群智能优化算法具有随机性，为尽量提高对比结果的可信度，所有函数的维数均取D=30维，且每个函数均用4种算法各自独立优化30次，取30次优化的平均结果作为对比指标。

4.3参数设置

关于本文提出的QIFA，引入量子计算机制后，增加了一个控制参数θ0，同时省略了位置更新式（3）中的随机项系数α，因此控制参数个数与普通FA是相同的。由于ODFA和FA的控制参数相同，仅是寻优策略不同，因此可以采用相同的参数。经过反复实验，最终确定的参数如下。

四种算法的共性参数为：种群规模NP=50；空间维数D=0；个性参数设置为：对于QIFA，β0=0.1，γ=1.0，θ0=0.05π；对于普通FA和OD⁃FA，α=0.5，β0=1.0，γ=10-5；对于VSSFA，采用文献［2］中建议的参数设置α=0.4，β0=γ=1.0。

4.4对比结果

由于本文提出的QIFA，需要计算旋转矩阵，计算量较大，因此首先考察相同迭代步数下QIFA与FA的优化性能对比。迭代步数取1000，每个函数采用两种算法分别优化30次的平均结果对比如表2所示。

在表2中，粗体数字表示该结果优于对比算法的结果。由此可知，QIFA的所有28个函数的优化结果均优于FA，实验结果充分展示了QIFA的优势。以函数5、8、10、24为例，两种算法30次优化的平均结果随迭代步数的变化情况如图1所示。

为充分验证QIFA的优势，有必要在相同运行时间下对比优化结果。因此，在下面的仿真中，在保持QIFA迭代步数不变（仍然为1000步）的前提下，将FA、VSSFA、ODFA三种算法的迭代步数均设为5000步，然后将每种算法分别独立运行30次，四种算法的平均结果对比如表3所示。

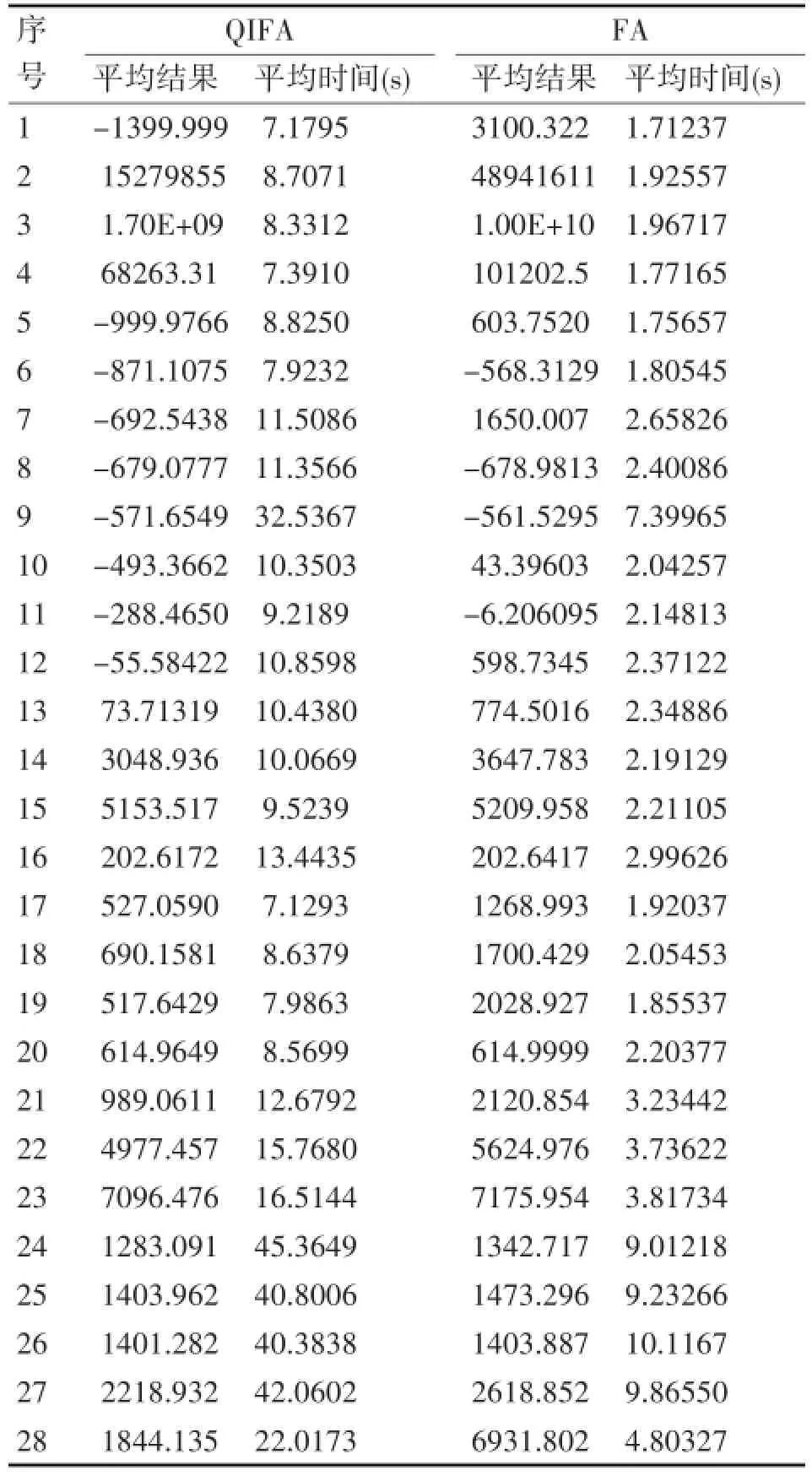
表2 QIFA和FA每个函数30次优化的平均结果对比

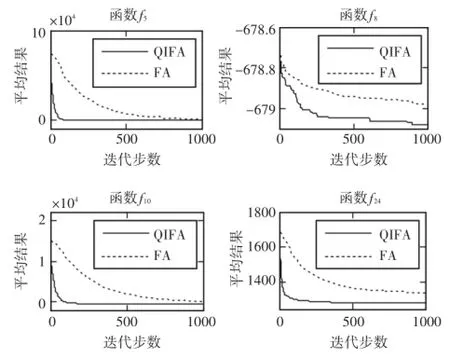
图1 两种算法30次优化的平均结果对比

在表3中，QIFA列的粗体数字表示该结果是四种算法中最优的。而其他三列中的粗体数字表示该结果优于QIFA算法。由此可知，QIFA优于FA的函数个数为23个，优于VSSFA的函数个数为21个，优于ODFA的函数个数为18个。实验结果表明QIFA明显优于三种对比算法。

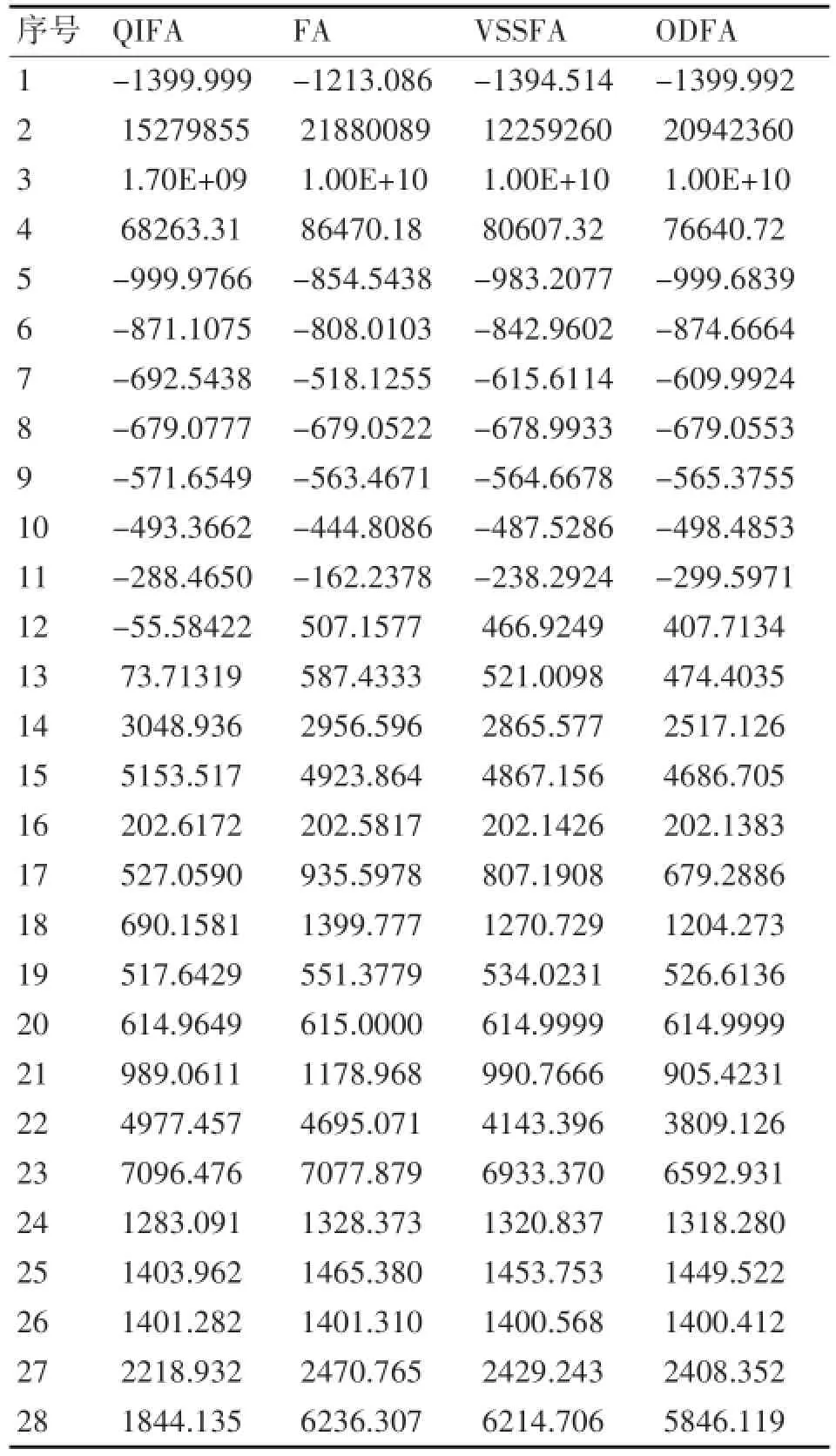
表3 四种算法每个函数30次优化的平均结果对比

4.5对结果的分析

在28个测试函数中，前5个函数为单峰函数，这类函数寻优难度较低，除变量不可分离的F2外，对于其他4个，QIFA均优于对比算法。对于15个基本多峰函数函数F6-F20，除F11和F17外都是变量不可分离的。这些函数寻优难度较大，除F6，F10，F11，F14-F16外，对于其他9个，QIFA均优于对比算法。对于最后8个变量不可分离的复合函数，寻优难度最大，此时QIFA仍有4个函数优于对比算法。实验结果进一步揭示了量子计算机制的引入对寻优能力提高的促进作用。

QIFA的优良性能在于其编码方式和寻优机制。首先，基于Bloch球面描述的量子比特的编码机制，将优化变量的每一维数值，都映射为Bloch球面上的某一点。这样就将传统方法中优化变量在优化空间每一维上的线性搜索，转化为Bloch球面上的搜索。根据Bloch球面性质，优化空间中全局最优解每一维的数值，都对应于Bloch球面上的一个圆周。只要搜索到该圆周上的任意一点，都等价于找到了该维的全局最优解。因此这种编码方式在一定程度上提高了QIFA获得全局最优解的概率。第二，QIFA的搜索机制采用了量子比特绕轴旋转的方法，这种方法可以自动实现量子比特的两个相位参数θ和φ的最佳匹配，从而保证了量子比特在Bloch球面上沿着最短路径向着目标位置逼近，而基于萤火虫飞行机理的旋转角度确定方法，有效提高了种群的多样性，一定程度上可以避免早熟收敛，从以进一步提升了QIFA的搜索能力。

5 结语

普通萤火虫搜索算法是仿生智能优化领域的新成员，其搜索能力有待于进一步提高。本文尝试将量子计算机制引入萤火虫搜索算法，用量子比特编码个体位置，用量子比特在Bloch球面上的绕轴旋转代替经典萤火虫搜索算法在优化空间中的随机游动，以期较大幅度地提高其优化能力。实验结果表明，这种尝试是成功的，新算法的确呈现出明显优于原算法的性能，从而揭示出，在原算法中引入量子计算机制，是提高其优化性能的有效途径。

［1］Yang X S.Nature-inspired metaheuristic algorithm［M］. London：Luniver Press，2008，148-172.

［2］Shuhao Yu，Shenglong Zhu，Yan Ma，Demei Mao.A vari-able step size firefly algorithm for numerical optimiza⁃tion［J］.Applied Mathematics and Computation，2015，263（15）：214-220.

［3］Adil B，Fehmi B O.Adaptive firefly algorithm with chaos for mechanical design optimization problems［J］.Applied Soft Computing，2015，36：152-164.

［4］Prakash V，Deepti A，Tejna P.Opposition and dimensional based modified firefly algorithm［J］.Expert Systems With Applications，2016，44：168-176.

［5］Hui Wang，Wenjun Wang，Xinyu Zhou，et al.Firefly al⁃go-rithm with neighborhood attraction［J］.Information Sci-ences，2017，（382-383）：374-387.

［6］Manvir K，Smarajit G.Network reconfiguration of un⁃bal-anced distribution networks using fuzzy-firefly algo⁃rithm［J］.Applied Soft Computing，2016（49）：868-886.

［7］Jothi G，Hannah I H.Hybrid Tolerance Rough Set-Firefly based supervised featureselection for MRI brain tumor im⁃age classification［J］.Applied Soft Computing，2016，46：639-651.

［8］Bartosz K.One-class classifier ensemble pruning and weighting with firefly algorithm［J］.Neurocomputing，2015，150：490-500.

［9］Kanimozhi T，Latha K.An integrated approach to region based image retrieval using firefly algorithm and support vectormachine［J］.Neurocomputing，2015，151：1099-1111.

［10］Ozgur K，Jalal S，Sepideh K，et al.A survey of water level fluctuation predicting in Urmia Lake using support vector machine with firefly algorithm［J］.Applied Mathematics and Computation，2015，270：731-743.

［11］Nguyen C L，Phayung M，Herwig U.A highly accurate firefly based algorithm for heart disease prediction［J］. Expert Systems with Applications，2015，42：8221-8231.

［12］Amir H，Hossein B，Saeed R，et al.Firefly optimization algorithm effect on support vector regression prediction improvement of a modified labyrinth side weir's dis⁃charge coefficint［J］.Applied Mathematics and Computa⁃tion，2016，274：14-19.

［13］Xiujuan Lei，Fei Wang，FangXiang Wu，et al.Protein complex identification through Markov clustering with firefly algorithm on dynamic protein-protein interaction networks［J］.Information Sciences，2016，329：303-316.

［14］Giuliano B，Giulio C，Giuliano S.Principles of quantum computation and information（Volume I：Basic concepts）［M］.Singapore：World Scientifi，2004.100-112.

［15］Liang JJ，Qu BY，Sugamthan P N，et al.Problems defi⁃ni-tion and evaluation criteria for the CEC 2013 special ses-siononreal-parameteroptimization［EB/OL］. Http：//www.ntu.edu.sg/home/EPNSugan/index files/CEC 2013/CEC2013.htm.

Quantum-Inspired Firefly Search Algorithm

LIU XiandeYU RuifangLI BinxuZHAO SiyuanLI Panchi
（School of Computer and Information Technology，Northeast Petroleum University，Daqing163318）

In order to improve the search ability of firefly search algorithm，by introducing the quantum computing mechanism into the classical firefly search algorithm，a quantum-inspired firefly search algorithm is proposed.In the proposed algorithm，the qubits are used to encode individuals，the Pauli matrixes are employed to determine rotation axis，the firefly flight principle is app⁃plied to obtian rotation angle，and the rotation of the qubits on the Bloch sphere is used to update the individuals.The experimental results of extreme optimization of benchmark test functions show that the proposed algorithm is obviously superior to the classical firefly search algorithm in optimization ability.

bionic intelligent optimization，swarm intelligence optimization，firefly algorithm，quantum-inspired optimiza⁃tion，algorithm design

TP183

10.3969/j.issn.1672-9722.2017.05.002

2016年11月17日，

2016年12月21日

国家自然科学基金（编号：61502094）；黑龙江省自然科学基金（编号：F2015021）；东北石油大学研究生创新科研项目（编号：YJSCX2016-030NEPU）资助。

刘显德，男，博士，教授，研究方向：量子智能计算、量子图像处理。于瑞芳，女，硕士研究生，研究方向：量子智能计算、量子图像处理。李滨旭，女，硕士研究生，研究方向：量子智能计算。赵思远，女，硕士研究生，研究方向：量子智能计算。李盼池，男，博士，教授，研究方向：量子智能计算、量子图像处理。