基于邻域漂移的点云法向估计算法研究
2021-04-02王茜微
张 杰, 刘 建, 王茜微
(辽宁师范大学 数学学院,辽宁 大连 116029)
近几年来出现的各种三维激光扫描仪和深度照相机,使得点云成为许多实际应用的焦点,法向是点云中一个重要的几何属性.高质量的法向有助于诸多点云处理算法,例如曲面重建、点云分割、点云去噪以及特征描述等.虽然近年来涌现出大量法向估计的算法,但由于噪声和非均匀采样的影响,快速准确地恢复点云的尖锐特征仍然是一个具有挑战性的工作.
点云的法向估计算法可分为基于Voronoi/Delaunay算法[1-2]、基于法向修正的算法[3-4]和基于局部邻域拟合法.基于Voronoi/Delaunay算法是利用三角剖分建立数据间的拓扑关系,然后基于重建出来的拓扑关系重建法向.这类算法对噪声比较敏感,无法处理大噪声及尖锐特征.基于法向修正的算法主要是一种基于平滑化的滤波方法,虽然这类方法在尖锐特征处可以得到较为理想的结果.但这类方法对输入的初始法向要求较高,当尖锐特征处的初始法向存在严重的光滑和污染,基于法向修正的算法无法准确地恢复模型的尖锐特征.
基于局部邻域拟合法是由Hoppe等人[5]首次提出的,该方法主要是利用主成分分析法(Principal Component Analysis, PCA)对邻域结构进行分析.当曲面是光滑的,PCA可以准确地估计点云的法向.但对于尖锐特征点,在拟合时由于受到位于其他光滑曲面上点的影响,导致估计的法向过于光滑.为了进一步提高法向估计的结果,Guennebaud 等人[6]利用代数球对邻域进行拟合;Pauly 等人[7]利用高斯权对邻域点进行加权,对距离当前点较近的邻域点,赋予较大权重;Yoon 等人[8]利用统计学的集成技术改进PCA算法的鲁棒性.以上的改进方法要求在加权和邻域的放缩过程中是各向同性的,但位于不同光滑曲面的点仍然会对拟合的结果产生影响.
理想情况下,与当前点位于不同光滑曲面上的点应被忽略.近年来鲁棒性技术[9-12]、子空间分割技术[13-15]以及深度学习[16-20]都被引入法向估计中来对邻域进行正确的选择.上述各类点云法向估计方法,在法向估计的性能和效率上得到一定提升.然而,这些方法都是利用以当前点为中心的邻域进行法向估计.由于在尖锐特征附近,曲面是由两个甚至多个光滑区域拼接而成,以当前点为中心的邻域并不适合用于法向估计.
近期一些学者[21-22]受到图像滤波方法[23]的启发,选择以非当前点为中心的邻域进行法向估计.Cao等人[21]将尖锐特征点分为边点和角点.对于角点,利用自适应增长模式构造一种完全嵌入在单一光滑曲面的邻域.对于边点,利用带方向约束的各项异性邻域构造算法,构造一系列包含当前点的候选邻域,并利用协方差分析对候选邻域的“平坦程度”进行刻画,最终选择一中心尽量靠近当前点,且较为平坦的邻域,用于法向估计.Zhou等人[22]将包含当前点的邻域作为候选邻域,然后对每一候选邻域求解一最优拟合平面,并利用邻域内点到拟合平面的距离对邻域的“平坦程度”进行刻画.虽然文献[21-22]都得到较好的效果,但用于生成候选邻域[21]或用于计算邻域“平坦程度”[22]的时间消耗较大,不适合实际应用.
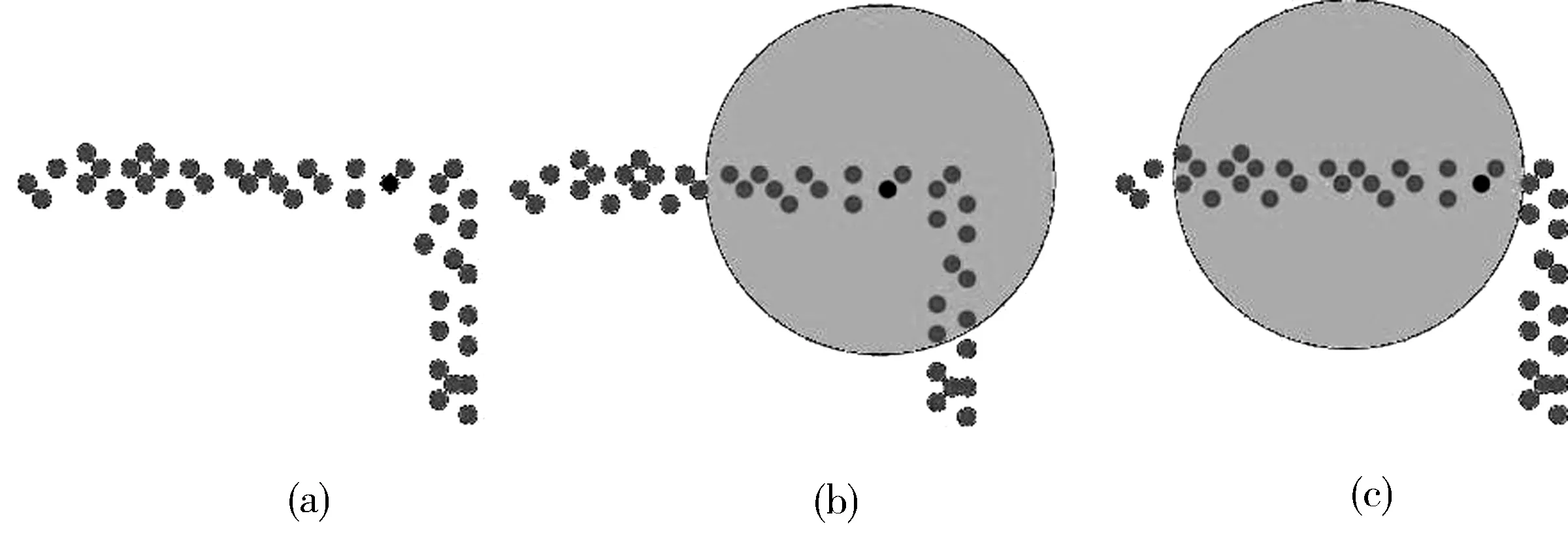
图1 以当前点为中心的邻域和邻域漂移结果的比较(a)输入的噪声点云;(b)以当前点的k个近邻点构造的邻域;(c)以漂移后的非当前点的k个近邻点构造的邻域Fig.1 Comparison of the neighborhood centered on the current point and the results of shifted neighborhood(a)The input noise point cloud; (b)The neighborhood constructed by k-nearest neighbors of the current point; (c)The neighborhood constructed by k-nearest neighbors of the shifted point
本文采用邻域漂移的思想,设计了更为简洁高效的算法用于候选邻域生成和邻域“平坦程度”计算.首先,以往算法在候选邻域的构造过程中强调候选邻域要包含当前点.本文将这一条件放宽,只要求候选邻域的中心点充分靠近当前点,将当前点的所有近邻点所对应的邻域作为候选邻域.这样对于一给定的邻域,只需要判断其中心点与当前点之间的距离即可,不需要利用搜索法查找当前点是否在该邻域中,运算效率更高.其次,虽然PCA在尖锐特征区域估计的法向过于平滑,但该算法能较好地刻画点的分布情况,且在运行速度上具有显著的优势[5,13].本文利用PCA对候选邻域的“平坦程度”进行评价,在确保准确性的情况下,有效地提高了算法的计算速度,实验结果表明本文提出的方法在精度上与当前的前沿算法持平,但在运行速度上有明显的改进,实用性较强.
2 算 法
2.1 特征点的选取
对每点pi计算其大小为k的邻域Ni,如图1(a)所示.对于邻域Ni,本文采用与文献[11-12,21]相同的运算方法估计每个点的初始法向和特征权重,并利用特征权重将所有点分为光滑点和候选特征点,为了文章的完整性,将对该过程做一个简单的介绍,具体过程见文献[11-12,21].
首先对于点pi计算其局部邻域Ni的协方差矩阵,协方差矩阵定义为
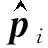
其中,0≤λ0≤λ1≤λ2是协方差矩阵Ti的奇异值.特征权重ωi刻画了点pi位于尖锐特征的概率.ωi=0,表示pi为光滑点,远离尖锐特征,其邻域Ni为一平面.当ωi大于给定的阈值ωt时,将pi定义为候选特征点.ωt利用文献[11-12,21]的方法自动估计.
2.2 候选特征点的法向估计
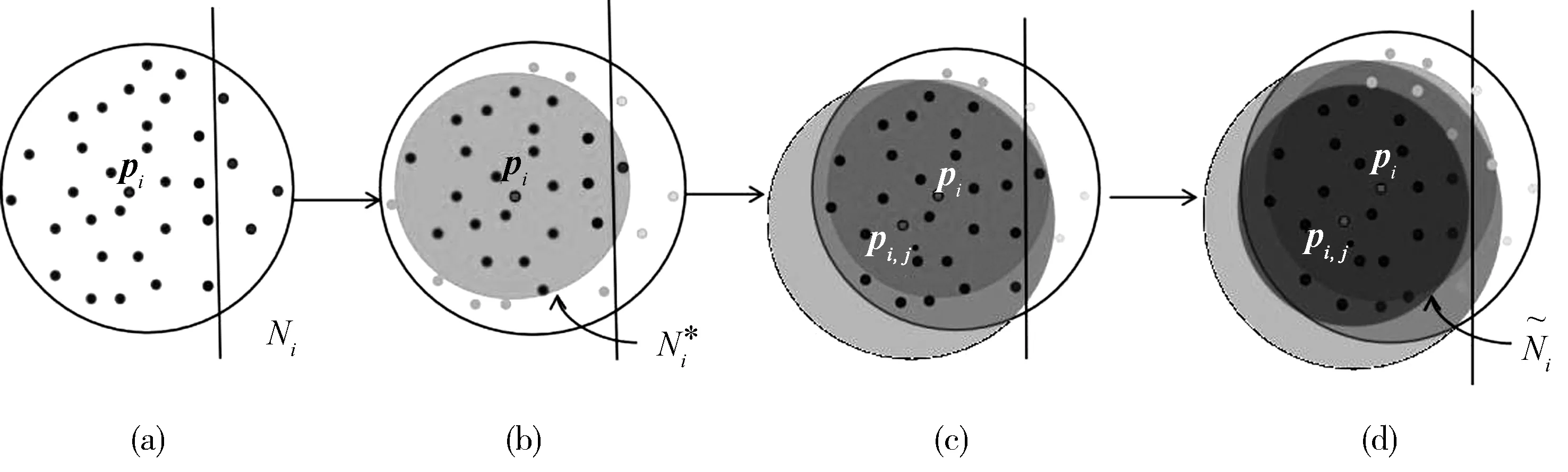
图2 算法流程图(a)选取候选点pi的k个近邻点构成邻域Ni,尖锐特征边用黑线表示;(b)候选点pi的k*个近邻点构成邻域最终所选点pi,j的k个近邻点构成邻域,浅灰色圆圈表示,邻域仍跨越尖锐特征;(d)为pi,j的k*个近邻点构成最终的邻域Fig.2 Algorithm flowchart (a) Given a candidate feature point pi, we select a neighborhood Niof size k.The sharp feature is represented by the black line. (b) For pi, we select a smaller neighborhood of size k*. (c)pi,jis the selected point. Its neighborhood with size k(represented by grey circle) may across borders. (d) For pi,j, we select a smaller neighborhood of size k* to construct the final
对于候选特征点,其邻域大都是由多个光滑曲面拼接而成的,PCA拟合而成的平面与候选特征点所在的局部平面存在较大偏差,估计的初始法向会过于光滑.因此,需要重新构造用于法向估计的邻域.
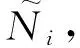
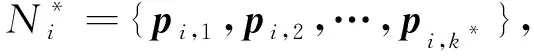
Ν={Ni,1,Ni,2,…,Ni,k*}.
Ν内任意候选邻域都对应一特征权重,该权重的计算方式如2.1节所述.将所有的特征权重构成的集合记为:ω={ωi,1,ωi.2,…,ωi,k*}.为了使得所选的候选邻域Ni,j内的所有点都位于同一光滑曲面,需找到特征权重集合中的最小值ωi,j*,其所对应的点pi,j*为最终选用点:
pi,j*=arg min{ωi,j|j=1,2,…,k*}.
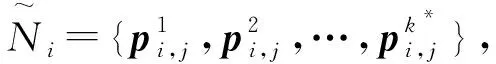
2.3 确定法向
3 实验结果及分析
为了评估算法性能,将本文的点云法向估计算法与一些具有代表性的、经典的算法及当前前沿算法进行比较,包括PCA[5]、RNE[9]、HF[16]、HoughCNN[17]、PatchShift[22]、LRRFast[14]、PCV[15].其中,HoughCNN使用作者提供的已训练好的HoughCNN_5s模型,该模型同时使用5个邻域尺度(32, 64, 128, 256, 512).HF根据不同的采样策略共有3个版本.根据以往实验,HF_cubes在运算性能和计算效率上表现更优,本文选择HF_cubes进行比较.
本文测试了包含多种光滑曲面和尖锐特征的合成模型,并对这些模型添加了均值为0的高斯噪声,其标准差定义为点间平均距离的百分比,分别为30%, 40%, 50%, 60%.
3.1 参数的选择
本文算法主要有2个参数,分别为
k: 用于计算初始法向的邻域点的个数.
k*: 用于计算候选特征点法向的邻域点的个数.
其中,噪声的大小决定k和k*取值,当噪声越大时,k和k*的值越大.在实验中k=100,k*=k/2.其他方法邻域点个数均设为100.所有算法的其余相关参数都采用默认值.
3.2 评价函数
与LRRfast、HF_cubes等算法相同,本文使用具有阈值的均方根误差(RMS_τ)[11-12]对计算结果进行定量的评价,如下所示:
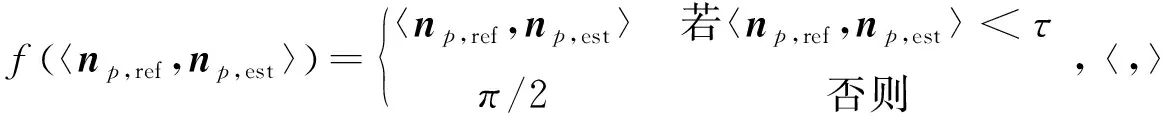
3.3 结果分析
图3和图4展示了不同算法在各个模型上RMS_τ的变化情况及均值.图5给出不同算法在多个模型上的可视化结果.
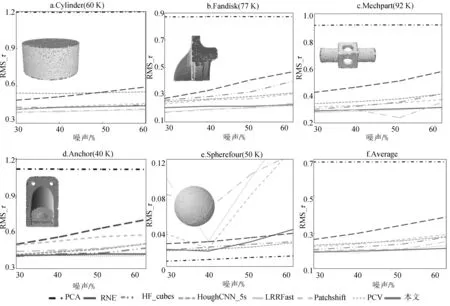
图3 不同模型上的RMS_τ值随噪声的变化情况Fig.3 RMS_τ value on different models with various noise
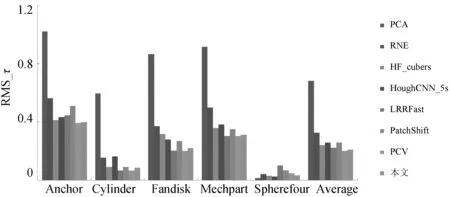
图4 不同模型上的RMS_τ均值Fig.4 The averageRMS_τof various methods
如图5所示,即使在非均匀采样的情况下, PCA算法仍能准确估计光滑曲面的法向信息(如图5中第6行和第7行所示).但是该算法在尖锐特征处估计的法向过于平滑,其RMS_τ值亦远远大于其他算法.这主要是因为PCA是利用整个邻域对切平面进行拟合.但在尖锐特征处,点的邻域大多是由两个以上光滑曲面拼接而成.在拟合时受到其他光滑曲面上点的影响, PCA算法无法准确地恢复出尖锐特征处的法向.
RNE和HF_cubes在尖锐特征处的效果要优于PCA(如图5中前5行所示),且在尖锐特征模型上的RMS_τ值低于PCA(如图3(a)~图3(d)所示).但当处理比较复杂的邻域结构时所估计的法向仍稍有光滑(如图5中第3行所示).
HoughCNN_5s使用了当前流行的深度学习算法,且通过考虑多个邻域尺度来提高算法性能.但当输入数据具有特殊属性时,需要重新训练网络模型.从图5所示的结果来看,Hough_CNN_5s在尖锐特征处仍稍有光滑,且其RMS_τ值要高于 LRRfast和PCV.
LRRfast、PatchShift和 PCV可以很好地恢复各种尖锐特征(如图5中前5行所示).但是在处理光滑曲面时,计算的法向具有较大偏差(如图5的第6行和第7行所示),导致RMS_τ值较高(如图3(e)所示).
本文算法在不同模型和噪声上都得到了较好的结果.在具有尖锐特征的模型上,本文算法的效果与LRRfast、PatchShift和 PCV持平(如图3(a)~图3(d)及图5的前5行所示),且其在所有模型上的RMS_τ均值与PCV持平并低于其他所有算法(如图4所示).对于光滑曲面(如图3(e)所示),其RMS_τ值与 PCA 基本持平,且明显低于其他算法.

图5 不同算法法向估计结果的可视化比较Fig.5 Visualization of estimated normals via various methods
3.4 时间比较
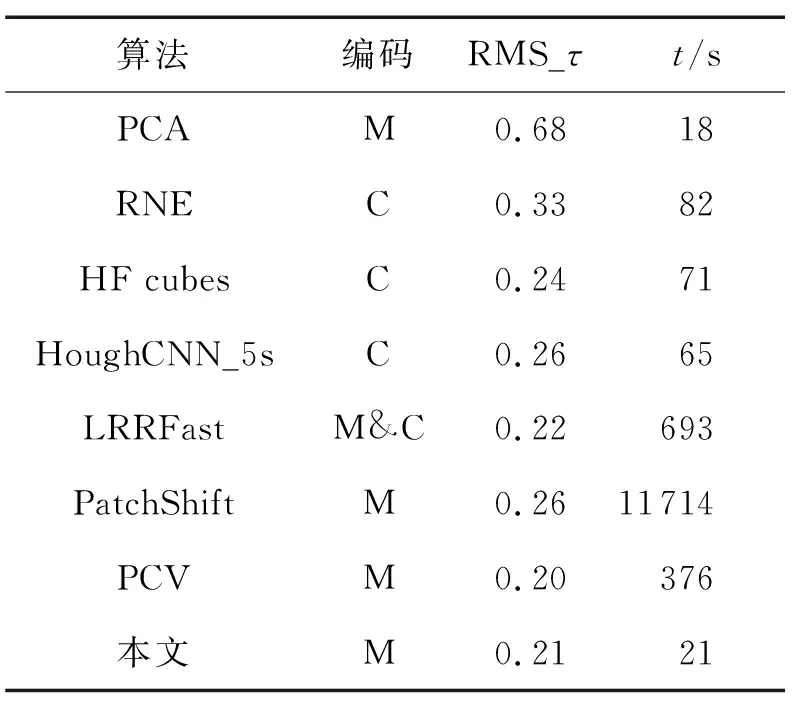
表1 不同算法的RMS_τ均值和时间均值的比较
表1展示了不同算法的RMS_τ均值及时间均值.所有实验所使用的电脑配置为1CPU Intel(R) Core i3 (TM) 2.4GHz.由于PCA算法较为简单,即使在MATLAB 实现下,其运行速度也是最快的.但PCA估计的法向过于光滑,无法准确对尖锐特征进行刻画.使用C/C++实现(表中记为“C”)的算法(RNE,HF_cubs,HoughCNN_5s)速度也较快.而其中使用 MATLAB 实现(包括MATLAB 和C/C++ 混编实现的表中记为“M&C”)的PCV算法的时间消耗仅好于LRRFast和PatchShift.本文算法的时间消耗仅次于PCA,但其性能显著高于PCA,且RMS_τ值与PCV和LRRfast相持平,显著好于其他算法.总之,本文算法能更好地兼顾输出的法向的质量与计算速度.
4 结 论
本文提出一种基于邻域漂移的法向估计算法,实现快速准确的法向估计.对于位于尖锐特征边附近的点,该算法首先通过k-近邻搜索和协方差分析,在当前点附近寻找一最优邻域,该邻域远离尖锐特征,但靠近当前点,可以对当前点所在曲面的结构进行有效刻画.然后对最优邻域使用PCA算法,获得最终法向.本文算法在确保法向估计准确性的基础上,最大程度缩短运行时间,提高算法效率.但本文算法没有考虑尖锐特征情况下的非均匀采样问题.如何在确保准确性和提高算法效率的基础上,考虑尖锐特征下的非均匀采样问题,这是未来的一项重要工作.
