数学编码的认知现象学分析①

王俊龙

(《高等学校文科学术文摘》编辑部,上海 200234)

数学编码的认知现象学分析①

王俊龙

(《高等学校文科学术文摘》编辑部,上海 200234)

从数学编码的角度探讨0的数学的、逻辑的和哲理的内涵,或者,是从数学编码的角度对空缺现象的一种认知,并把这样一种认知看作现象学的内容之一。所以,对空缺的认知及其数学编码也可视为认知现象学范畴之内的。文章重点论述空缺的数学表示,围绕空缺的数学编码讨论了一些相关的问题:如何表示空缺?八卦的逻辑内涵是什么?布尔代数的运算是封闭的吗?极端存在的状态是什么样的?空位如何表示?存在0内代数吗?布尔代数与广义太极代数(含太极代数)的差别是什么?

认知现象学;数学编码;布尔代数;太极代数;广义太极代数

发现太极代数是近些年的事。[1]布尔代数与太极代数相比较,最大的差异在于,前者中的0表示空类(或空集),后者中的0表示真类(或绝对全集)。[2]228-234从布尔代数到太极代数,这中间的跳跃太猛、变化太快、转弯太急。因此,人们既缺乏必要的心理准备,也缺乏必要的认知准备,从而造成理解上的巨大障碍。从布尔代数到太极代数，存在诸多认知内容和环节。比如,涉及《周易》中的数理的认知,[3]也涉及与实数系的关联[4]。

本文从数学编码的角度探讨0的数学的、逻辑的和哲理的内涵,或者,是从数学编码的角度对空缺现象的一种认知。把这样一种认知看作现象学的内容之一,应该是可以的。所以,对空缺的认知及其数学编码也可视为认知现象学范畴之内的。

一 空缺的表达

空缺是一个常用词,空缺与空白、缺口相仿。比如,填补空白、缺口。空缺本身没有内容,因此提出这样一个问题:数理上如何表达空缺呢?

数学上,通常用0表示空位。比如,100表示个位和十位空缺。由于布尔代数是借用了算术中的乘法单位元1作为逻辑乘法单位元,借用算术中的加法单位元0作为逻辑加法单位元,因此,布尔代数也借用0表示空缺(空集)。[5]关于0表示空位,下文将有进一步的讨论。

但是,太极代数显示,逻辑上无法计算空缺的大小。逻辑上无法直接用逻辑变量表示空缺或缺口,因为空缺或缺口本身是没有任何内容的。因此只能用列示实有部分的方式来间接地暗示空缺的部分。这与绘画时描画空的容器所釆用的方式是一样的,必须要先实际地画出一个容器(实物),以此容器内部尚未被任何东西填实来暗示其空缺部分。

算术上采用的方式是:统一地用正数表示实有的数量,用负数表示亏空的数量。

生活中难免的遗憾往往也是留下空缺造成的,遗憾什么呢?只能以对实在的否定加以表达,比如,错失了复试机会,错过了比赛时间。所采用的否定式方法与算术中采用负数的方式是相仿的。

不妨以A、B、C三个实物所能产生的空缺为例。

(一)未编码图象

1.A实在,B、C皆空缺,见图1-1-1。

2.A空缺,B、C皆实在,见图1-1-2。

3.B实在,A、C皆空缺,见图1-1-3。

4.B空缺,A、C皆实在,见图1-1-4。

5.C实在,A、B皆空缺,见图1-1-5。

6.C空缺,A、B皆实在,见图1-1-6。

7.A、B、C皆实在,见图1-1-7。

8.A、B、C皆空缺,见图1-1-8。

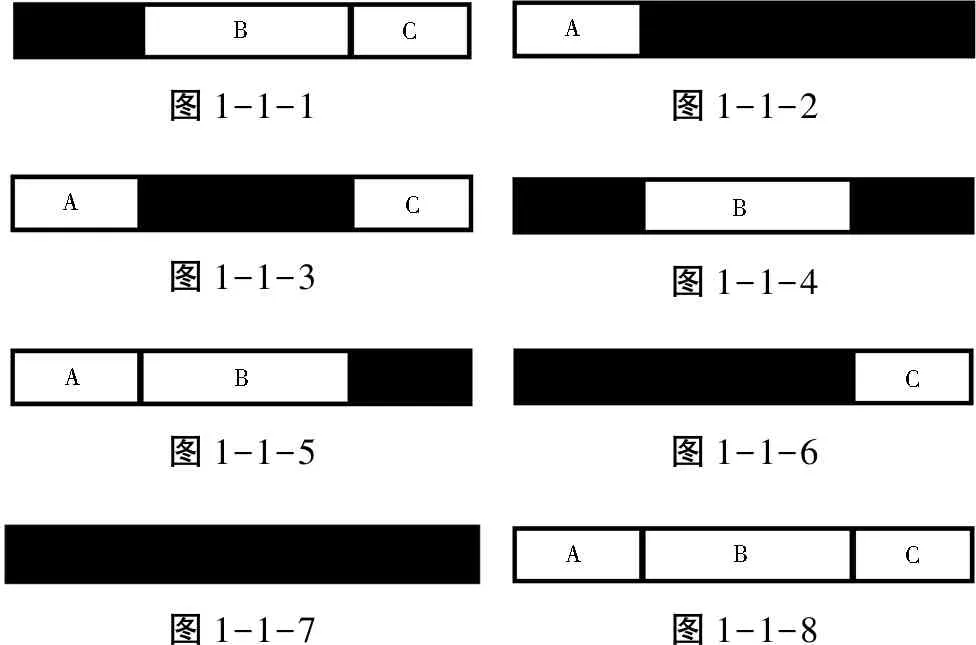
图1-1-1图1-1-2图1-1-3图1-1-4图1-1-5图1-1-6图1-1-7图1-1-8

其中图1-1-7和图1-1-4分别表示连续和空缺的两个经典图象,前者为阳爻,后者为阴爻。

(二)简单的编码图象(标实未标虚)

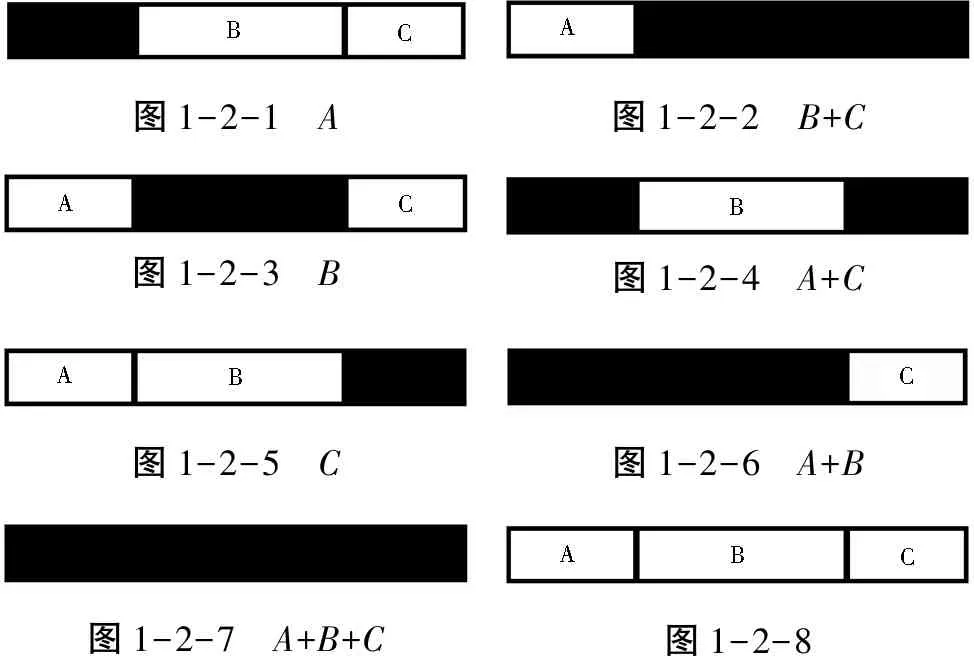
图1-2-1 A图1-2-2 B+C图1-2-3 B图1-2-4 A+C图1-2-5 C图1-2-6 A+B图1-2-7 A+B+C图1-2-8

如图1-2，约定:图中黑色部分为实,白色部分为虚。下同。

(三)精确的编码图象(虚实皆标)

当A+B+C为相对全集(有限集)的情形

图1-3-1 A(-(B+C))图1-3-2 (-A)(B+C)图1-3-3 B(-(A+C))图1-3-4 (A+C)(-B)图1-3-5 (-(A+B))C图1-3-6 (A+B)(-C)图1-3-7 A+B+C图1-3-8 -(A+B+C)

如图1-3，其中-(A+B+C)表示A+B+C空缺。此种情形下,A+B+C是无限集的一个子集。而且不难发现,图1-3-1和图1-3-2并非真正互补的图形。同样,图1-3-3和图1-3-4,图1-3-5和图1-3-6,它们都不是两两互补的图形。甚至图1-3-7和图1-3-8也不是真正互补的图形。

对于A+B+C为绝对全集的基本性质,将在下文讨论。

(四)理想的编码图象(虚实皆标)

当A+B+C为绝对全集(最大无限集)的情形

图1-4-1 A=-(B+C)图1-4-2 -A=B+C图1-4-3 B=-(A+C)图1-4-4 -B=A+C图1-4-5 C=-(A+B)图1-4-6 -C=A+B图1-4-7 A+B+C图1-4-8 -(A+B+C)

如图1-4，其中-(A+B+C)表示A+B+C的补,是绝对补集。此种情形下,A+B+C是无限集的一个子集。而且不难发现,图1-4-1和图1-4-2是真正互补的图形。同样,图1-4-3和图1-4-4,图1-4-5和图1-4-6,它们都是两两互补的图形。图1-4-7和图1-4-8也是真正互补的图形。

若A+B+C为绝对全集,则A+B+C不是任何一个实在的对象。下文将讨论绝对全集的基本性质。

二 八卦的编码图象(逻辑编码)

当A+B+C为绝对全集(最大无限集)的情形

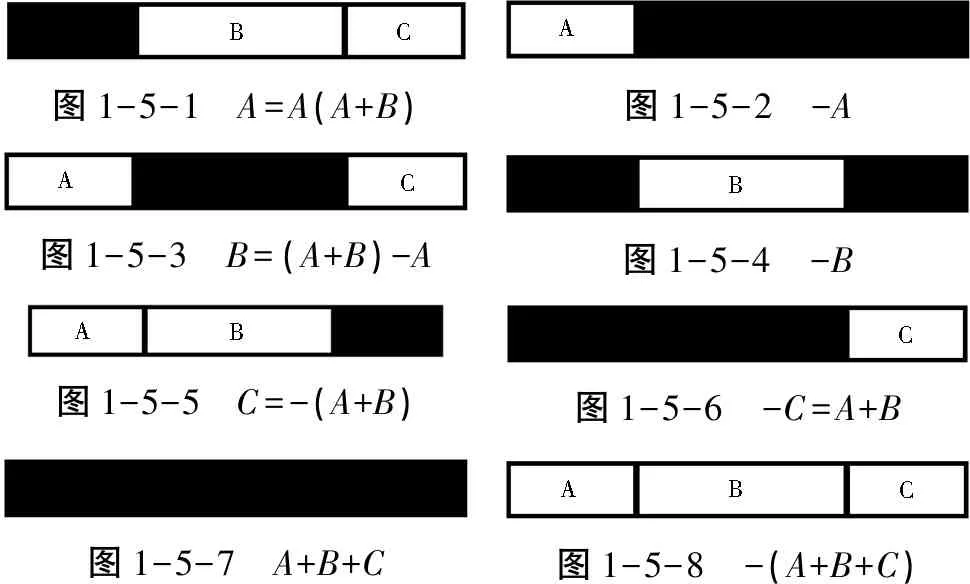
图1-5-1 A=A(A+B)图1-5-2 -A图1-5-3 B=(A+B)-A图1-5-4 -B图1-5-5 C=-(A+B)图1-5-6 -C=A+B图1-5-7 A+B+C图1-5-8 -(A+B+C)

如图1-5，其中,这里A、B、C两两互异不交。

图1-5-6引进了析取运算,即逻辑加法。图1-5-1引进了合取运算,即逻辑乘法。图1-5-3引进了减法运算,此为逻辑减法(含对称差)。

B=(A+B)-A,(A+B)-A=(A+B)(-A)。

八卦是八个逻辑公式,其中离卦表示合取(与)运算,坎卦是其补,表示与非。其中巽卦表示析取(或)运算,兑卦是其补,表示或非。其中艮卦表示对称差(环和),震卦是其补。

虽然八卦引进了与、或、差及补运算,对于经典的逻辑运算已经是大致满足了。但是,八卦并没有构成一个运算封闭的代数系统。如果要构造一个完全封闭的逻辑代数系统并不是一件容易的事情。在太极代数和广义太极代数发现以前,人类尚没有真正建构完成完全封闭的逻辑代数系统。

三 并非封闭的运算:布尔代数的编码真相

布尔代数被认为是一个运算封闭的逻辑代数系统,事实果然如此吗?

不妨以A代表所有1以内的数,A+B代表所有10以内的数,A+B+C代表所有100以内的数。如图2。这里A、B、C两两互异不交,且A+B+C构成有限集。

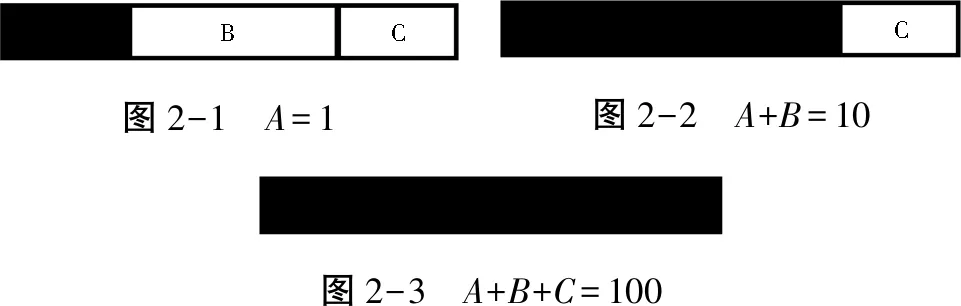
图2-1 A=1图2-2 A+B=10图2-3 A+B+C=100

下面具体讨论相对全集的基本性质。

(一)布尔代数:1以内的数

布尔代数可归结为1内代数,1是最大数,-1是1的补,-1又表示是1的空缺。但是,-1≠0。以为-1=0是严重错误的。

因为,空缺与空集不是同一个概念。空集是任意集合的子集。空缺是具体对象的空缺(离场、不在场)。

-1表示1不在场,或-1表示不包含1以内的任何数。

-1表示对特定对象或范围的否定,而并非对任意对象或范围的否定。所以,-1≠0,假如其中的0表示真正的空集。因为,0否定的范围比-1要大得多。

(-1+1)×1=1(使实在限定于1)

(-1)×1+(-1)=-1(使空缺限定于-1)

-((-1+1)×1)=-((-1)+1)+(-1)=(-1)×1+(-1)=-1

可见,现行布尔代数是有隐蔽的约束条件的,这就是布尔代数的真相。

严格来说,若布尔代数中的全集是有限集,则布尔代数的全部运算不可能是闭的。换言之,如果不能证明布尔代数的全集是最大的无限集,则现行布尔代数是不能成立的。

(二)扩展的布尔代数*关于扩展的布尔代数,参见王俊龙:《论语言研究需要怎样的逻辑工具》,《山西大学学报》2013年第5期，第57-61页。:10以内的数

布尔代数的全集是有限集,因此,其全集未必是1。比如,布尔代数的全集可以是10。

1以内的数有两个极端情形:

1不是任何一个1以内的数,此范围定为1；

没有任何一个1以内的数,此空缺定为-1。

10以内的数有两个极端情形:

10不是任何一个10以内的数；

没有任何一个10以内的数。

此时,10是10以内数中的最大数。此种情形下,全集不再是1，而是10。

这就说明,布尔代数在1内是不封闭的。

(三)扩展的布尔代数:100以内的数

布尔代数的全集也可以是100。

100以内的数有两个极端情形:

100不是任何一个100以内的数；

没有任何一个100以内的数。

此时,100是100以内数中的最大数。此种情形下,全集不再是1,也不是10,而是100。

这就说明,扩展的布尔代数在10内是不封闭的。可以推知,扩展的布尔代数在100内也是不封闭的。

进一步可以推知,扩展的布尔代数在任何一个足够大的有限数内(比如2的1000次方)都是不封闭的。

那么,是否存在一个对于任何数封闭的逻辑代数系统呢?如果宇宙是一个封闭的世界,那么了解它就需要一个完全封闭的逻辑代数系统。尽管西方数学在近现代取得了突飞猛进的巨大进步,但是,西方数学至今尚没有真正做到对于一个完全封闭的逻辑代数系统的建构。

四 空和无:极端存在的逻辑表达

负100与欠100是同一个意思吗?

100-1与99是同一个意思吗?

-100+1与-100+(100-99)一样吗?

上述问题已经超出布尔代数的范围。解决上述问题需要引进太极代数和广义太极代数。

为了引进太极代数和广义太极代数,必须先了解极端存在及其逻辑表达。

前文引出相对全集和绝对全集这两个概念。对于相对全集似乎容易理解,但是,如果不先了解什么是绝对全集,就会对相对全集产生诸多误解。

什么是绝对全集?绝对全集与绝对空集是一对极端的逻辑概念。

最简单的说法是,绝对全集是什么都有,绝对空集是什么都没有。

换一种说法,绝对全集是“什么也不是”,绝对空集是“什么都没有”,它们是一对极端的逻辑概念。

从空缺的角度看,“什么都没有”是最大的空缺。这一空缺需要无所不有才能填补。因此,绝对全集与绝对空集是逻辑互补的两个极端。

什么都不是,称之为无。什么都没有,称之为空。空和无是一对绝对存在。

相对全集是绝对空集与绝对全集之间的有限集。

下面是几组极端存在的概念表达的示例。

第一组:

大一,至大无外。

小一,至小无内。

极限状态。*惠施曰:“至大无外,谓之大一。至小无内,谓之小一。”

无,不是任何东西。

空,没有任何东西。

存在状态。

第二组:

无限,不是任何空间。

无空,没有任何空间。

空间两极。

永恒,不是任何时间。

没空,没有任何时间。

时间两端。

第三组:

0,不是任何量。

-0,没有任何量。

数量形态。

真类(V),不是任何集合。

空类,没有任何集合。

集合形态。

第四组:

无为,不是任何作为。

不为,没有任何作为。

作为状态。

公心,不是任何私心。

无私,没有任何私心。

私心程度。

第五组:

白条,不是任何账单。

免单,没有任何账单。

账单形态。

无税,不是任何税。

免税,没有任何税。

课税状态。

第六组:

全力,不是任何力量。

无力,没有任何力量。

努力程度。

全职,不是任何职务。

免职,没有任何职务。

履职状态。

需要说明的是,绝对状态并不限于上述列举的范围。而诸绝对状态存在说明,绝对状态广泛存在于人类的认知活动和社会活动中。

惠施曰:“至大无外,谓之大一。至小无内,谓之小一。”这里的大一其逻辑意义与《周易》中“太极生两仪”的太极相同,也与《老子》所言“天下万物生于有,有生于无”中的无相同。可见,中国先秦哲学中的大一、太极和无,正如《老子》所说“同出而异名”。

五 0内代数:太极代数和广义太极代数

存在1以内的数,也存在10以内的数,100以内的数,乃至无穷大以内的数。那么,有必要发出一个认知现象学的追问:存在0内的数吗?

上文通过极端概念及其表达,不难发现,0是一个极端数,它不是任何量。同时,它不是任何量并不意味着它没有任何量。

如果存在0内的数,那么,就要证明0比任何实数都要大。

为什么不是任何量的0比任何实在量要来得大呢?不难发现,对于任意实在量x,存在-x,且x+(-x)=0。因为x+(-x)既不是x,也不是-x。这就说明,x+(-x)=0不是任何实在量,且比任何实在量来得大。

没有任何量是有别于不是任何量的另一个量的极端。没有任何量,这样一个极端数是什么呢?是0的相反数,就是-0。

存在所有事物的共性吗?回答是肯定的。

共性:ABC=S,S就是共性!

因为空属于任何事物,所以,空是所有事物的共性之一。

因为所有事物都包含于无中,所以,属于无也是所有事物的共性之一。

任何事物属于无,任何事物包含空。这是所有事物必有的两个共性。

众所周知,在算术运算中,-0=0。但是,在逻辑上,需要引进一个有别于0的一个新的极端量,正是-0。并且,逻辑运算显示,-0≠0。

太极代数和广义太极代数证明,一切量存在于空(-0)和无(0)之间。0是最大数,-0是最小数。

六 空位的表达:布尔代数和太极代数的比较

空位的数学表达是一个十分基本的问题。目前,已知有两种方式表示空位。一是布尔代数的0,0表示空。二是太极代数的0,0表示无。

布尔代数是如何表达空位的?用一个0。100,010,001。空集是000。0是空缺的意思,且0是占位的。1+0=1,表示1与0析取显示1。可见,在布尔代数中,空是占位的,叫空位。

太极代数可以表达空位吗?也用一个0。【100】*这里【x】表示特定的逻辑变量,以区别于人们通常熟悉的代数变量x。参见王俊龙:《〈周易〉经传数理研究》,北京:人民出版社,2015年版,第1、143页(注释部分)。,【010】,【001】。但是,全集是【000】。【0】是无量的意思,且是占位的,但不显示任何量。【1】×【0】=【1】,表示【1】与【0】合取显示【1】。

【-0】表示空,【1】+【-0】=【1】,【1】与【-0】析取显示【1】。但是,【-0】是不占位的,因为没有任何量。就是说,太极代数中空缺是不占位的!

《老子》曰:“三十辐共一毂,当其无,有车之用。埏埴以为器,当其无,有器之用。凿户牖以为室,当其无,有室之用。故有之以为利,无之以为用。”

可见,老子用其无,布尔用其空。

七 逻辑编码的适用对象

数学与实在的关系,数学是认知工具,实在是认知对象。

实在是可以认知的,意味着是可以编码的!只有达到可以编码的程度才可以说对实在有所认知。实用物品可编码意味着还可以实施网络控制技术,物联网技术是例证。

目前为止,以下认知的对象大致已经达到逻辑编码的程度:

时间可以逻辑编码(见上述第二组);

空间可以逻辑编码(见上述第二组);

颜色可以逻辑编码(见太极代数)[2]159-160;

命题可以逻辑编码(见布尔代数);

集合可以逻辑编码(见上述第三组);

存在可以逻辑编码(见上述第一组);

自然数可以逻辑编码(见广义太极代数)[2]230-234

逻辑图可以逻辑编码(见太极代数)[6];

布尔代数可以逻辑编码(见太极代数);

太极代数可以逻辑编码(见广义太极代数);

人体形态可以逻辑编码…(见太极代数)[6]

当然,达到逻辑编码程度的认知对象不止上述列举的内容。

八 结论

综上所述,空缺的数学表达关涉认知现象学的核心内容。由于对空缺认知的差异,也由于对数理认知的差异,关于空缺的数学编码技术也是有差异的。不过,有一点是清楚的了,布尔代数作为逻辑编码技术是有其局限性的。相比较而言,太极代数和广义太极代数在逻辑编码方面有广泛得多的应用。这是因为,太极代数和广义太极代数是建立在-0(空)和0(无)之间的逻辑代数。而空和无是一切存在的两个极端表现,或者说,一切现象存在空与无之间。

通过空缺表达的认知现象学分析,有助于人们理解一种新的数学观,甚至也有助于人们理解一种新的世界观。布尔代数和广义太极代数(含太极代数)其实是两种世界观的产物。前者的立论基础是有无矛盾论(或实在论),后者的立论基础是太极阴阳思想(或阴阳和合论)。[2]157-158一切数量存在于-0(空)和0(无)之间,预示着一种新的逻辑代数:太极代数和广义太极代数。一切现象存在于空与无之间,预示着一种新的世界观。

[1]王俊龙.论太极代数及其辩证内涵[J].湖南师范大学社会科学学报,2009(3)：43-47.

[2]王俊龙.《周易》经传数理研究[M].北京：人民出版社，2015.

[3]王俊龙.《周易》数理是什么？[J].西南大学学报,2016(2)：19-27.

[4]王俊龙.广义太极代数：R 上的逻辑代数[J].湖南师范大学自然科学学报,2014(5)：85-89.

[5]方景龙,王毅刚.应用离散数学[M].北京：人民邮电出版社，2005 :7.

[6]王俊龙.人体形态逻辑:生物逻辑学研究[J],湖南师范大学自然科学学报,2012(2)：76-81.

(责任编辑 郭庆华)

An Analysis of Mathematical Coding from Perspective of Cognitive Phenomenology

WANG Jun-long

(ThePeriodicalOfficeofChinaUniversityAcademicAbstracts，Shanghai200234,China)

From the perspective of mathematical coding,this paper discusses the mathematical,logical and philosophyical connotations of 0,a kind of cognition of vacancy phenomenon regarded as one of the contents of phenomenology.Therefore, the cognition of vacancy and its mathematical coding can also be viewed as cognitive category of phenomenology.The paper focuses on the mathematical representation of vacancies,discussing some related problems around the mathematical coding of vacancy：How to represent vacancy？What is logical connotation of eight hexagrams?Is Boolean algebra operation closed? What is extreme state of the existence?How to represent vacant position?Does algebra exist within 0?What are the differences between Boolean algebra and general Tai Chi algebra (including Tai Chi algebra)?

cognitive phenomenology；mathematical coding；Boolean algebra；Tai Chi algebra；general Tai Chi algebra

2016-10-30

王俊龙(1959-),男,江苏盐城人,博士,《高等学校文科学术文摘》杂志社研究室主任、副研究员，主要从事教育学、心理学和语言文字学编辑工作，以及《周易》数理研究。

10.13451/j.cnki.shanxi.univ(phil.soc.).2017.02.002

B089;O141

A

1000-5935(2017)02-0008-06

① 第八届华东现象学青年论坛暨“现象学与认知科学”研讨会(2016年11月5-6日,中国巢湖)参会论文,本文可视为从现象学角度认识数理逻辑问题的一次新尝试,这里发表时保持原文不变。