例谈对数函数中的典型错解及教学建议
2017-06-01吴小丽
◎吴小丽
(西华师范大学,四川 南充 637002)
例谈对数函数中的典型错解及教学建议
◎吴小丽
(西华师范大学,四川 南充 637002)
对数函数是高中数学学习的一种重要函数,函数本身就综合性、抽象性强,对于高一学生刚接触到此种新型函数,难免会出现各式各样的错误,研究解题中的错误、充分发挥错解的潜在功能,对于提高教学质量是十分有意义的.
对数函数;错解;教学建议
一、忽视定义域而导致解题出错
(一)利用单调性解不等式
例1 已知函数f(x)=lg(x+1),解关于x的不等式0 (二)复合函数中的单调性与最值 例2 若y=loga(2-ax)在[0,1]上是减函数,则a的取值范围是________. 错解分析 大部分学生一看到底数是字母a,立刻想到分类讨论,复杂易错,还有很大一部分学生忽视了定义域为[0,1],在[0,1]上要真数大于0. 正解 ∵a>0,∴-a<0,∴u=2-ax在[0,1]上为减函数.又∵y=loga(2-ax)在[0,1]是减函数,∴y=lgau在[0,1]为增函数,即a>1且2-a×1>0,∴1 例3 已知f(x)=2+log3x,x∈[1,9].求函数y=[f(x)]2+f(x2)的最大值及y取得最大值时的x的值. 错解分析 大部分学生能够得出y=(log3x+3)2-3,令t=log3x,则y=(t+3)2-3,但直接认为定义域就为[1,9],从而得到t∈[0,2],进而得到错误答案.其实由1≤x≤9且1≤x2≤9得,函数y的定义域为[1,3],从而t∈[0,1].用到换元时,一定要注意新元的取值范围,因此,正确求得复合函数的定义域显得尤为关键. 例4 (1)已知函数y=log2(x2-2kx+k)的值域为R,则k的取值范围为________. (2)已知函数y=log2(x2-2kx+k)的定义域为R,则k的取值范围为________. (1)错解 由题意,x2-2kx+k>0在R上恒成立,所以Δ=4k2-4k<0,即0 正解 由题意,在定义域内,真数x2-2kx+k能取得所有大于0的值,所以Δ=4k2-4k≥0,即k∈(-∞,0]∪[1,+∞). (1)的错解即为(2)的正解. 错解分析 在R上为增函数,很多学生考虑不全面,只考虑到每段为增,还要保证整体单调,即要考虑在分段点处的大小关系.实际上是学生对单调性的概念没有真正理解. 根据学生在对数函数相关习题中的错解,可以发现大多数是因为对数函数的相关概念理解不透,其次,不能运用数形结合等数学思想方法来分析题意,数学思维能力比较薄弱.对此,提出以下几点教学建议.(1)数学学习中,概念学习是基础,教师应注重数学概念的教学.将抽象的数学概念与生活实际相结合,做到循序渐进,一点一点强化.(2)应加强学生作图的训练.很多题只要能快速画出草图,就能使本身抽象难懂的题目变得简洁易懂,思路也会开阔许多,从而使解题更快捷简便.(3)应加强数学思想方法的渗透.让学生了解更多数学思想方法,可以从多角度去思考问题.(4)加强学生数学思维能力的培养.很多高一学生数学思维还停留在初中,对于一些难度稍大的题目便束手无策,教师应适当引导,加强对其数学思维能力的培养,使其能更深地思考问题进而提高学习能力. [1]郑云霞.对数函数常见解题误区[J].中学生数理化(高一版),2011(22):17. [2]王海清.发挥错解潜在功能 提高数学教学质量[J].湖州师范学院学报,1998(5):74-81.二、混淆定义域与值域而导致解题出错
三、对分段函数的单调性考虑不全而出错
四、不能数形结合而导致解题困难

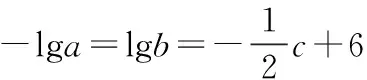
五、教学建议
