数学美的和谐性研究之一
——从“数学悖论”的消除中发现数学潜在的和谐美
2017-06-01曾瑞海
◎曾瑞海
(汕头职业技术学院,广东 汕头 515041)
数学美的和谐性研究之一
——从“数学悖论”的消除中发现数学潜在的和谐美
◎曾瑞海
(汕头职业技术学院,广东 汕头 515041)
本文借助三个数学悖论,从消除悖论的过程中发现数学潜在的和谐美,进而提高认识数学和谐美的目的.
数学悖论;和谐性;连续;无穷小量
尽管各种数学悖论产生的历史背景不同,表现形式各异,但它们都是某一数学理论原有体系中蕴藏着矛盾的反应.人们面对数学悖论的产生而着手对数学概念进行重塑,对不完善的理论进行改进,进而产生了新的数学观念,完善了思维方法,推动了数学理论的发展,在更高的层次上实现了新的和谐统一与完善.因此,数学悖论是促使数学理论不断追求和谐、不断趋于完善的一种重要的推动力,是给数学的发展带来新的生机和希望的火种.
由此可见,数学自身显然是从不和谐走向和谐的.
一、从“连续悖论”的消除中发现数学潜在的和谐美
我们知道,“连续”是高等数学中一个重要的基本概念,但是它的现代定义的表达却是经历了一个从不和谐到和谐的漫长过程.
数学家欧拉曾认为,由一个单独解析表达式给出的函数是连续的,而由几个表达式给出的函数即分段函数是不连续的.
但我们又知道,傅立叶已经证明,定义在某个区间上的任意函数都可以表示成该区间上的正弦函数与余弦函数的无穷级数.
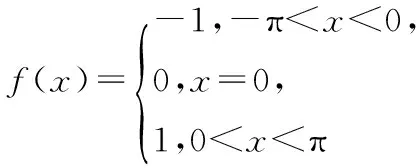
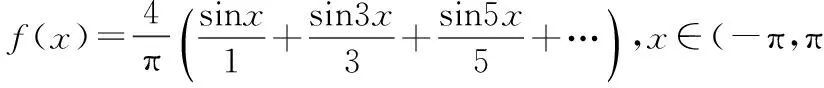
上述函数依照欧拉对连续的定义,既是不连续的,同时,又是连续的.显然这是一个悖论.
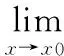
二、从“贝克莱悖论”的消除中发现数学潜在的和谐美
数学史上把贝克莱的问题称之为“贝克莱悖论”.笼统地说,贝克莱悖论可以表述为“无穷小量究竟是否为0”的问题:就无穷小量在当时实际应用而言,它必须既是0,又不是0.但从形式逻辑而言,这无疑是一个矛盾.
1734年,大主教乔治·贝克莱(George Berkeley)以“渺小的哲学家”之名出版了一本标题很长的书《分析学家;或一篇致一位不信神数学家的论文,其中审查一下近代分析学的对象、原则及论断是不是比宗教的神秘、信仰的要点有更清晰的表达,或更明显的推理》.在这本书中,贝克莱对牛顿的理论进行了攻击.
他指责牛顿,在其理论中,无穷小量一会儿说是零,一会儿又说不是零.
举例来说,为计算某函数的导数,比如,说x3的导数,先将x取一个不为0的增量Δx,由(x+Δx)3-x3,得到3x2·Δx+3x·(Δx)2+(Δx)3,后再被Δx除,得到3x2+3x·(Δx)+(Δx)2,最后突然令Δx=0,求得导数为3x2.这是“依靠双重错误得到了不科学却正确的结果”.因为无穷小量在牛顿的理论中一会儿说是零,一会儿又说不是零,因此,贝克莱嘲笑无穷小量是“已死量的幽灵”.贝克莱的攻击抓住了牛顿理论中的缺陷,是切中要害的.
18世纪粗糙的,不严密的工作也导致谬误越来越多的局面,不谐和音的刺耳开始震动了数学家们的神经.
从1821年开始,柯西陆续出版了几本具有划时代意义的书与论文.其中给出了分析学一系列基本概念的严格定义.比如,他开始用不等式来刻画极限,使无穷的运算化为一系列不等式的推导.这就是所谓极限概念的“算术化”.柯西的工作使分析基础严密化迈出了第一大步.
在柯西的努力下,连续、导数、微分、积分、无穷级数的和等概念也建立在了较坚实的基础上.不过,在当时情况下,由于实数的严格理论尚未建立起来,所以柯西的极限理论还不可能完善.
柯西之后,魏尔斯特拉斯、戴德金、康托尔各自经过自己独立深入的研究,都将分析基础归结为实数理论,并于70年代各自建立了自己完整的实数体系.魏尔斯特拉斯的理论可归结为递增有界数列极限存在原理;戴德金建立了有名的戴德金分割;康托尔提出用有理“基本序列”来定义无理数.
三、从“蒙提·霍尔悖论”的消除中发现数学潜在的和谐美
问题提出:假设你正在参加一个游戏节目,你被要求在三扇门中选择一扇.其中一扇后面有一辆车,其余两扇后面则是山羊.你选择了一扇门,假设是1号门,然后,知道门后面有什么的主持人开启了另一扇后面有山羊的门,假设是3号门.然后,他问你:“你想选择2号门吗?”那么,改变你的选择对你来说是一种优势吗?
数学少不了悖论,数学公理系统没有悖论就不是完备的,我们不是去容忍悖论而是去消除悖论,在消除悖论的过程中提高认知水平.数学教学中常常因为悖论的思考复杂性而弃置不用,笔者相信悖论的使用不仅不会增加难度,反而会使问题更富趣味性和研究性,更有利于激发学生对数学学习的兴趣;有利于向学生介绍重要的数学思路;有利于开发丰富多彩的数学学习活动;有利于帮助学生洞察数学问题的解题过程;有利于培养学生辩证的、开创性的、批判性的思维方式;有利于提高学生对现代数学所具有的美妙、多样,甚至幽默性质的鉴赏力.从这个意义上说,没有悖论的数学学习是危险的,没有悖论思想的数学教学是苍白的.数学家同时也是悖论大师,悖论不是目的,以悖论为手段学会创新才是目标.
[1]李雍.数学和谐美[M].大连:大连理工大学出版社,2009.
[2]陶理.关于数学悖论的认识问题[J].东北师大学报(哲学社会科学版),1993(6):80-84.
[3]王方汉.历史上的三次数学危机[J].数学通报,2002(5):42-43.
[4]王秀芳,郝素娥.论数学悖论的思维特色[J].山西大学师范学院学报(综合版),1993(2):39-43.
[5]吴振奎,吴旻.数学中的美[M].上海:上海教育出版社,2002.
[6]张媛媛.试论数学的和谐美[J].开封大学学报,2013(2):65-67.
