“知识溯源”驱动解题教学——以证明两线垂直为例

◎刘锦梅

(南京师范大学附属苏州石湖中学，江苏 苏州 215100)

“知识溯源”驱动解题教学
——以证明两线垂直为例

◎刘锦梅

(南京师范大学附属苏州石湖中学，江苏 苏州 215100)

解题教学是数学教学的重要组成部分，是学以致用的一个重要环节.在解题教学中，教师如何帮助学生快速找到解题的突破口是一项重要任务.多数情况下，对于要解答的一个数学问题，探寻真正解法的过程并非一帆风顺，而是曲折起伏，但是探寻正确解法的思路却“有规可依”“有序可循”：那就是从分析题目的已知和所求入手，看看条件能想到什么？看看所求需要什么？通过“知识溯源”式的问题驱动开展教学，引导学生学会从“怎样做”转向“怎样想”，从而从根本上提高学生分析问题和解决问题的综合能力.本文以一道证明题为例，谈谈笔者在教学中探究该题解法的心路历程.

一、题目呈现

如图1，△ABC，△ACD，△BDE均是等腰直角三角形，AC与BD相交于点F，连接EF交AD于点M，连接EC交BD于N点.求证：MN⊥BD.

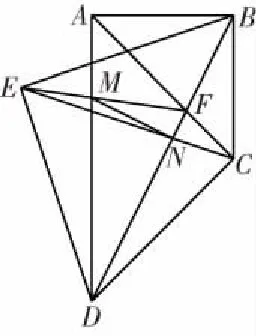
图1

图2

二、证法展示

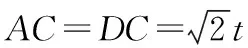
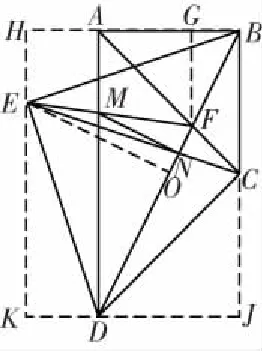
图3

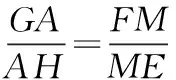
图4

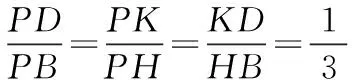
三、证法分析

教师在启发学生解题的过程中，不但要引导学生“怎样做”，还要分析“怎么想到这样做”.教师要一一呈现其思路的形成过程和必然性，仅仅引导学生掌握基本的分析模式，并由此指望学生自悟并有效迁移，当然只能取决于学生的顿悟了.

鉴于以上分析，笔者从知识溯源角度切入，以培养学生怎样想为前提，通过下列驱动问题逐步展开教学.

问题1：解题目标是什么？(证明两线垂直.)

设计说明：许多学生做了半天的题不知道要干什么，缺少目标分析意识，只一味地从条件入手联想，只有坚持从条件和结论两方面入手，方能得心应手.

问题2：本题是求证MN⊥BD，那么初中阶段学过的证明两线垂直的知识源有哪些？

主要有：(1)垂直的定义——证明两线所成角为直角；(2)等腰三角形三线合一；(3)勾股定理逆定理；(4)逆用中垂线的性质；(5)圆的切线垂直于经过切点的半径，等等.

设计说明：通过问题2驱动，意在培养学生灵活处理两线垂直问题的能力.

问题3：结合条件，本题应该选用哪个知识源来证明MN⊥BD？

本题直角比较多，易想到用垂直的定义证明，但直接证明这些直角与MNF相等却又不易；而由△BDE为等腰直角三角形，就不难想到构造辅助线，取BD的中点O，连接EO(如图2)，并利用MN∥EO来证明垂直了.

设计说明：上述两个问题的主要目的是通过知识溯源(即从知识转化的角度)引导学生掌握解决证明两线垂直的思考方向和处理策略，即先回顾某类问题的相关知识点，再结合题设确定解决具体问题所适用的知识点，从而明确解题方向.

问题4：证明两线平行有哪些知识源？本题适合用哪一种方法证明MN∥EO？

主要有：(1)平行线的判定定理(同位角相等、内错角相等、同旁内角互补，两直线平行)；(2)平行于同一直线的两条直线平行；(3)平行四边形的对边平行(含矩形、菱形与正方形)；(4)三角形(梯形)中位线定理；(5)平行线分线段成比例定理的逆定理，等等.本题从MN与EO的位置特征和要证角相等的目的来看，宜选择最后一个知识源证明.

设计说明：此问题的目的在于让学生掌握证明两线平行的几种方法.

问题5：如何证明四条线段成比例式(即比例的来源有哪些)？

主要有：(1)平行线分线段成比例；(2)相似三角形对应边成比例；(3)计算.

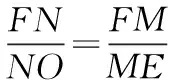
设计说明：意在培养学生证明对应线段成比例的能力.

一点建议：鉴于原题难度之大，添加辅助线之多，对于普通学生来说，其教学价值必将大打折扣.

不妨做如下修改：

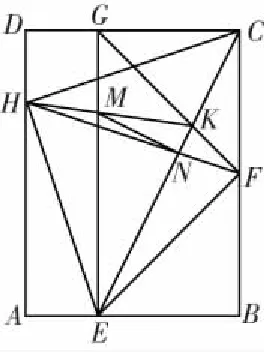
图5

如图5，在矩形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA上一点，且△CEH，△EFG和△FCG均为等腰直角三角形.设CE与GF相交于点K，连接HK交GE于点M.若CG=6.(1)求线段DH的长；(2)求KM∶MH的值；(3)设HF与CE交于点N，连接MN，求证：MN⊥CE.

四、两点感悟

从知识溯源角度切入，引导学生学会从“怎样做”转向“怎样想”.其优越性在于：

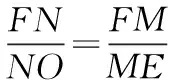
第二，提升学生的迁移能力.由于知识溯源是把解决此类问题的知识点一一呈现，不仅从中探求出解决本问题的策略，而且也为处理同类问题提供了思考方向，从而达到了“以题会类”的效果，提升了学生的迁移能力(见文献[1]).

总之，通过“知识溯源”驱动解题教学，不仅明确了解题方向，提升了迁移能力，更关键的是引导学生学会了“怎样想”，从而在真正理解的基础上达到灵活应用的境界.

[1]刘华为.从教“怎样做”到教“怎样想”[J].中学数学教学参考：中旬，2016(6)：26-28.