游弋在有疑与无疑之间

重庆两江新区金渝学校 杨开文

游弋在有疑与无疑之间

重庆两江新区金渝学校 杨开文

在小学数学课程指导中，要充分发挥启蒙教育这一思想，从而开启学生的思维大门，让学生对待问题能够有统一和适当的解决策略，从而强化学生对有关基础数学知识概念的理解和认识。将呆板的概念教学过程变成提出问题、解决问题、分析问题的思考流程，能够十分有助于学生综合能力的提高和进步。

有疑；无疑；小学数学

在进行小学数学课程指导中，单纯地依靠让学生做题、老师讲题，很难达到教学目的，只有让学生能够真正参与到疑难问题解析中，并完全投入思考，才能真正起到思想启蒙的作用，才得以提升学生的创造性思维，并强化学生的问题解决能力。下面就具体数学教学中有疑与无疑的两者之间转化的教学方式进行详细介绍。

一、学习无疑须有疑——生疑

在学生学习过程中要注意发现问题，要能结合教材内容提出疑问，提出疑问就代表了自己思考过，也只有思考过问题才能加深对知识的理解和记忆。

比如：一张花布长120厘米，宽96厘米，把它裁成同样大小的正方形布块且无剩余，那么布块边长最长多少厘米？一共可以裁多少块这样的布块？学生在拿到该题时不要直接看问题，而是先要想：由题目已知条件我能得到哪些有用信息？由此经过转化，该题也就是求120和96的最大公因数，结果是24，那么可得（120÷24）×（96÷24）＝5×4＝20（块），所以布块边长最长是24厘米，一共可以裁20块这样的布块。又比如：甲班科技书的本数是乙班的2倍，如果甲班拿出15本给乙班，这时，两班的科技书的本数一样多，那么两个班原有多少本科技书？在解决该题时学生要先提出疑问：甲班和乙班的书本数之间可以列出什么样的等式关系？在书本数的数量交换中具体交换内容又有哪些？先根据题目生疑进而罗列清楚题中条理，从而完成解题。由题可知15×2÷（2-1）＝30（本），30×2＝60（本），所以甲班原有60本书，乙班原有30本书。

在生疑的过程中主要要求学生能够辩证地看待问题，不能问什么就想什么，可以将问题内容与相关的概念结合起来，从而提高解题效率。

二、有疑定要求无疑——析疑

在提出了疑问后，便是对疑问的解决过程，在析疑的环节中，学生要清楚把握自己要解决的问题方向，要能够有着明确目标，并向着该目标去收集相关信息以供解答。

比如在学习小学数学人教版中“长方体周长、表面积”计算这一章节时，有：在一个长为2分米，宽1.5分米，高1.2分米的长方体木料的8个顶点各截去一个棱长为2厘米的小正方体，求剩下木料的表面积。该题看似有点摸不着头脑，但是学生在思考该题时要注意分析问题，题中所问的是截去后木料的表面积，我们在分析长方体的表面积概念含义后，便可总结出剩下木料的表面积和原长方体的表面积相等，所以就有表面积为：（2×1.5+1.5×1.2+2×1.2）×2=14.4（平方分米）。又如：把一根截面是正方形的长方体木料锯掉2.5厘米后，就成为一个正方体，这样表面积就减少了30平方厘米，求原来长方体木料的长。首先根据分析疑问点，我们可先从截面的周长计算着手，也就是30÷2.5=12（厘米），那么可得截面的边长为12÷4=3（厘米），所以就有原长方体的长为：3+2.5=5.5（厘米）。

在析疑的过程中，要先明确疑问点，并充分结合题中所给出的已知条件和各种有效信息，在整合这些内容的过程中找到解决疑问的突破口，该过程还有利于简化整体的解题流程，让解题思路变得更加清晰和完整。通过转化等思想达到无疑，除了体现在解题过程中，在学习课本中的基础概念时也一样适用。

三、无疑本自有疑始——明疑

在解决了疑问后，并不代表疑难点就完全没有了，我们要对解决后的疑问再深入挖掘，发现其存在的其他疑问点，在一层一层的递进思考中强化学生对相关内容的认识和了解，这对提高学生的思维能力和综合素质水平都有很大帮助。

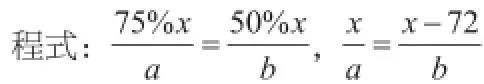
在学习小学数学中的行程问题时，这类题目往往涉及的方面较多，出题的类型也很多，我们要做到以不变应万变，从疑问中明白疑难点，进而对疑难点进行突破和深入认识，从而解决这一类型的问题。

四、有疑方能达无疑——释疑

找出了疑难点，还要对疑难点进一步总结和深挖，从而达到释疑的目的，也是完善和总结学生整个思维过程的必要环节。在思考问题时根据上述思考的流程，首先找出疑问，罗列题中所给的已知条件，然后根据该疑问点进一步选择解决方法，再对解决方式进行统一整理，最后完成这一类型的答疑。

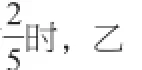
综上所述，在游弋在有疑与无疑之间的小学数学学习中，主要内容是在提出疑问与解决疑问两个方向中的不断运动，其目的是为了让学生能够多多思考问题，在思考问题的过程中让自己的理解得到深化，通过总结和整理建立健全的知识体系，从而进一步完善和增强自己的逻辑思维构建。