直角坐标系的运用拓展方法
2017-06-01江苏省南通市八一中学徐菊华
江苏省南通市八一中学 徐菊华
直角坐标系的运用拓展方法
江苏省南通市八一中学 徐菊华
平面直角坐标系是初中数学的重要组成部分,也是一种重要的数学思维方法——数形转换的思维方法。众所周知,一个直角坐标系就是一个平面,在平面上的任意一点只能是唯一的一个坐标与它相对应。点可以构成线,再组合成面,可见直角坐标系把几何变得数字化了,所以直角坐标系是数学的一种重要应用工具。本文从直角坐标系的运用谈谈拓展方法,仅供各位同仁商讨和调研。
直角坐标系;运用;拓展方法
用数轴可以清楚地描述直线上一点的位置;同样地,用直角坐标系也可以准确地描述平面上一点的位置。从家到学校经过的路径是平面特征的,不可能用直线来表示,所以地图、手机导航采用了直角坐标系的原理。用一个直角坐标系来表示一个平面,在平面上的任意一点只能是唯一的一个坐标与它相对应。那么,直角坐标系有怎样的运用呢?
一、在直角坐标系可以清楚地表示一个点的位置
【例1】 以学校为直角坐标系原点,方方家居住西北位置,到东西轴的距离是2公里,到南北轴的距离是3公里,请用直角坐标系来表示家和学校的相对位置。
【分析】 首先明确的是地理位置放在直角坐标系中,横轴和纵轴分别表示的意义是什么,家庭的方位在哪一象限,数轴上的单位是什么等要素。
【作法】 (1)如图建立平面直角坐标系;
(2)以学校为原点;
(3)水平为东西轴,竖直为南北轴;
(4)以1公里为1个单位长度。
通过案例与生活实际结合来激发学生的思维激情,通过数学知识运用拓展的过程,揭示直角坐标系的科学表达方法,把枯燥无味的数学知识转化为学生身边的话题,让学生在积极的探究中取得较好的学习效果。

二、在直角坐标系可以系统地表示一条直线的方向
【例2】 将教室按如图所示的方式建立一个直角坐标系。

请小组同学讨论:两个座位A与B,二者的纵坐标相同,而横坐标不同,则AB的连线与(南)北轴的关系是( )
A.相交 B.垂直 C.平行 D.以上都不正确
【分析】 首先明确A、B两个座位在教室中放在直角坐标系里的位置,横轴和纵轴的特征是什么,怎样在直角坐标系中得到AB的连线,最后确定AB的连线与北轴的关系。
【解析】(1)在直角坐标系中找出两个座位——A与B两个点的相对位置,注意二者的纵坐标相同,而横坐标不同;(2)连接A、B,如下图所示,判断AB的连线与北轴的关系为垂直,故选B。

此案例可以继续小组讨论:若两个座位A与B,二者的横坐标相同,而纵坐标不同:若两个座位A与B,二者的横坐标、纵坐标均不同等等。
本案例是最贴近学生实际生活的一个素材,把实际问题情境同数学中的直角坐标系的概念融合在一起,去探究点组成的直线在平面直角坐标系中的特征,让学生的思维得到最大程度的发散,让学生亲历数学运用过程来挖掘自己的学习潜能。在探究过程中采用小组合作的方式学习,让不同的思维在自主探究和合作交流中不断碰撞,形成团队智慧的结晶。
三、在直角坐标系可以完整地表示一个几何的特征
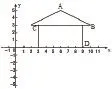
【例3】 小远想把如图所示的一个房子向下平移3个单位长度,怎样才能做到?请你帮助小远作出相应图案,并写出平移前后的有字母的点的坐标。
【分析】首先确定有字母的各点的坐标,然后理解什么是平移,向下平移是什么坐标在变化,最后确定平移后有字母的各点的坐标。
【解析】 向下平移是点的纵坐标发生变化,减小了,而横坐标不变化。可以得到的图案如右图所示,从而得出相应有字母的各点的坐标。这里答案就不再一一细说了。
本案例是为了培养学生在自主学习中质疑、解疑的能力,让学生养成悉心探究,细心发现的良好习惯。学生在做题后一定会领悟到若图中点的坐标为M(x,y),则平移后的坐标是M’(x,y-3)。这样,不仅驱动了学生参与的积极性,同时提升了学生敢于质疑、勇于归纳的探究精神。
总之,以上有关直角坐标系的案例仅是管中窥豹,其知识拓展还有很多,应用细节也还有很多,唯有让学生在今后的练习中不断去理解和锤炼,才能真正通过直角坐标系的运用来实现知识的升华。
[1]谭剑林.浅析数学思想在初中数学教学中的运用[J].数学学习与研究, 2012(6):33-33.
[2]李夏英.浅析在初中数学教学中渗透数学思想与数学方法的手段[J].考试周刊, 2013(A5):69-69.
[3]闫玉叶.谈初中“数形结合”思想在函数中的运用策略[J].数理化解题研究:初中版, 2012(11):24-25.