随机产出下数量柔性采购策略研究
2017-06-01何波,张霞
何 波,张 霞
(重庆大学经济与工商管理学院,重庆 400030)
随机产出下数量柔性采购策略研究
何 波,张 霞
(重庆大学经济与工商管理学院,重庆 400030)
本文研究制造商如何利用数量柔性采购管理供应商随机产出带来的风险。制造商的主要供应商的产出是随机的且单价较低,另外一个供应商以数量柔性合同方式提供产品给制造商且单价较高。分别讨论了确定需求和随机需求下制造商的采购策略,分析了不同条件下制造商的订货决策,得出了制造商单源订货和双源订货的条件。
供应不确定;随机产出;数量柔性合同
1 引言
随着全球化进程的加剧,原始设备生产商(Original Equipment Manufacturer)将制造业务外包给合同制造商(Contract Manufacturer)的生产模式已日渐成为企业的新选择。在中国,超过90%的家电企业实行制造业务外包[1]。一方面,制造业务外包使得OEM可以有效降低生产成本使企业致力于研发和营销,另一方面,制造业务外包使得OEM对CM的管理更加困难。例如:半导体等零部件生产的复杂性以及对精细化程度的高要求常常导致CM的随机产出。越来越多的OEM认识到管理CM的随机产出带来的供应风险具有重要意义。例如苹果公司的制造业务都是委托给富士康。但是近年来,苹果公司不断增加给另外一家合同制造商—和硕的制造订单。通过这种将制造外包分散化的策略,苹果公司能更好的管理供应风险[2]。
很多学者对合同制造商(供应商)随机产出给原始设备制造商(制造商)带来的供应风险管理策略进行了深入研究。Agrawal等[3]建立了分散订货的报童模型来管理供应风险。Krause等[4]研究指出在供应商产出状态实现前,加强与供应商之间的合作能有效降低供应不确定带来的负面影响。慕银平等[5]研究表明使用价格柔性合同能有效降低供应风险提高供应双方收益。Gupta等[6]研究了制造商竞争和供应风险环境下的紧急采购策略。Guo Shanshan等[7]提出在主要供应商的产出随机情况下,通过事先向后备供应商预定容量可以缓解主要供应商带来的风险。Babich[8]指出供应商资格审查或对供应商的可靠性进行投资能有效管理供应不确定性。李毅鹏等[9]研究了供需不确定下单零售商与多供应商组成的供应链的最优定价订货策略。也有文献提出在随机产出下通过供应链协调缓解供应风险[10-15]。
数量柔性合同是指制造商以批发价退还订货量的一部分给供应商。这种方式让供应商分担了一部分制造商库存过剩的风险,激励制造商订货,可以实现供应链协调。现有文献研究了随机需求下的数量柔性合同。郑克俊[16]指出通过建立基于期权契约与数量柔性相结合的决策模型可以提高制造商和零售商的利润实现供应链协调。Tsay[17]研究了多周期数量柔性合同下,供应链成员的行为与绩效关系。Sethi[18]研究了多供应商多周期的数量柔性合同模型。Tsay和Lovejoy[19]探讨了多周期不确定需求下数量柔性合同对供应商绩效的影响。Chung[20]研究了由两个供应商和一个零售商的组成的供应链,其中一个供应商提供柔性合同,另一个为提供固定批发价,他们分析了零售商的采购策略。如果供应商的产出是随机的,能否使用数量柔性采购降低供应风险?以上文献都没有进行这方面的讨论。仅有一篇文章分析了一个制造商采用柔性订货策略向一个产出随机的供应商订货的模型[21]。
不同于以上研究,本文研究了由一个制造商和两个供应商组成的分散式供应链。其中一个供应商为制造商长期合作的主要供应商,如苹果公司的合作伙伴富士康,其产出是随机的,称为风险供应商;另一个供应商以数量柔性合同方式提供产品给制造商,但价格较高,称为数量柔性供应商。制造商是否要从数量柔性供应商处采购?在什么条件下,数量柔性采购是一种更好的方式?制造商需要在成本和柔性之间取得平衡,才能有效管理供应风险。本文分别讨论了需求确定和需求随机下制造商的采购策略,分析了采购策略的结构性质,得出了实施单源采购和双源采购策略的条件,求出了不同条件下制造商的最优订货量。讨论了成本和柔性对制造商最优订货量和利润的影响。
2 模型与分析
考虑由两个供应商和一个制造商组成的供应链。其中一个是风险供应商(供应商1),当制造商向它订购Q单位产品时,由于随机产出的影响,它实际提供xQ单位产品。其中x是[0,1]之间的随机变量,其概率密度函数为f(x),分布函数为F(x),期望为μ1。为了降低供应风险,制造商以数量柔性采购的方式从另外一个供应商(供应商2)处采购产品。其单位价格比风险供应商的要高。制造商向供应商2预定q单位产品,当制造商获得从风险供应商处的订货后,制造商可以修改订货量为qm。根据数量柔性合同的要求,修改的订货量只能在一定的范围内:制造商可以至多取消βq单位的订货量,即至少订购(1-β)q单位的产品。制造商的最终订货量qm∈[(1-β)q,q],其中β∈[0,1]。制造商面临的总需求为D,本文先分析需求确定时制造商的决策,然后分析随机需求下制造商的决策。
2.1 参数及决策变量定义
本文用到的参数和决策变量如下:
w1供应商1的批发价格;
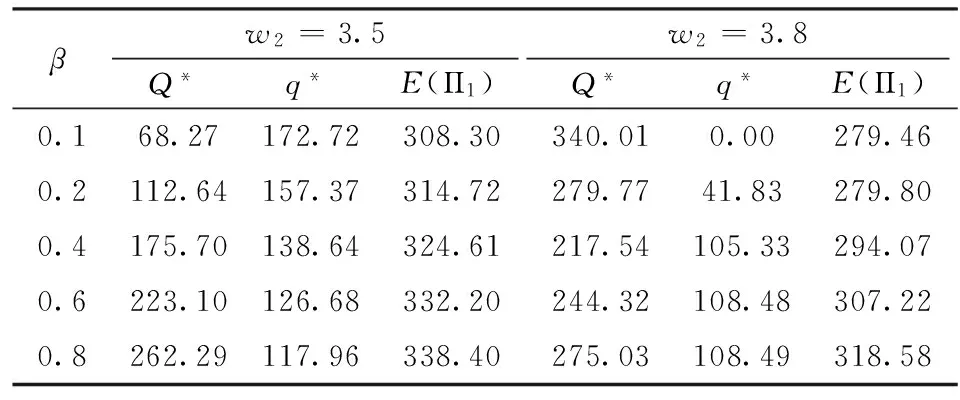
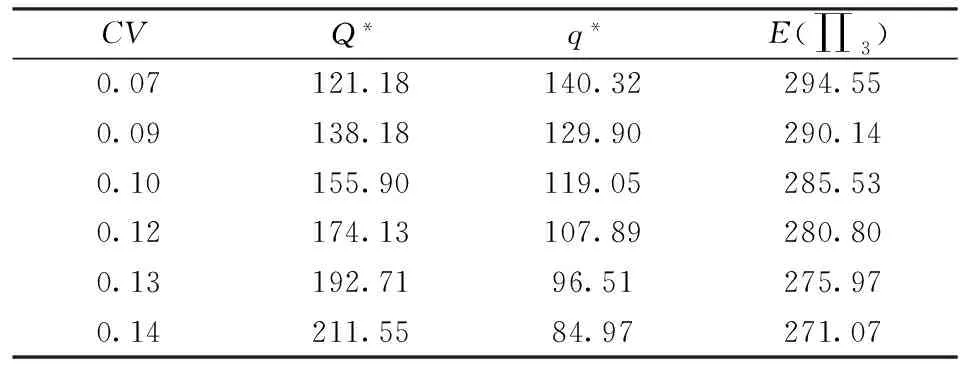
w2供应商2的批发价格,w1 pm制造商的单位缺货成本; v制造商的单位产品残值; p销售价格; D市场需求; Q制造商向供应商1的订购数量(决策变量); q制造商向供应商2提出的预购数量(决策变量); (1-β)q供应商2至少提供给制造商的数量; Π1需求确定时制造商实施双源采购的利润; Π2需求确定时制造商只向供应商1订货时的利润; Π3需求随机时制造商的利润。 2.2 需求确定下制造商的采购策略 制造商面临确定需求,它向供应商1以批发价订购Q单位产品,同时以数量柔性方式向供应商2 预定q单位产品。根据数量柔性合同的要求,当制造商预定量为q时,供应商2至多提供q,当然制造商最终至少购买(1-β)q。因此,制造商的利润函数为: Π1=pmin(D,xQ+q)-w1xQ-w2min(max(D-xQ,(1-β)q),q)-pmmax(D-xQ-q,0)+vmax(xQ+(1-β)q-D,0) (1) 其中第一项为制造商获得的总收入,第二项为制造商向供应商1订货的成本,第三项为制造商向供应商2订货的成本,第四项为制造商的缺货成本,最后一项为剩余产品的残值。为了与现实情况相符,参数需要满足下列关系:p>w2>w1>pm>v>0。经过化简,制造商的利润函数(1)式为: Π1=-(p+pm-w2)(D-q-xQ)+-(w2-v)(D-(1-β)q-xQ)+-(w1-v)xQ-(w2-v)(1-β)q+(p-v)D则期望利润函数为: (2) 我们首先分析(2)式的性质。 定理1 制造商的期望利润E(Π1)是关于Q和q的凹函数。 证明 对(2)式关于Q和q求导,得到: 通过验证海塞矩阵和其主子式|H1|和|H2|,我们得到: 因为海塞矩阵为负定,因此E(Π1)是关于Q和q的凹函数。 得证。 根据(1)式,制造商的优化问题为: 引理1 对于制造商而言,不可能存在Q*=0且q*>0。 证明 引入拉格朗日乘子λ1和λ2,拉格朗日函数为L(Q,q,λ1,λ2)=E(Π1)+λ1Q+λ2q,由KKT定理,有以下条件成立: 如果q*>0,由条件② 可得λ2=0,如果Q*=0,则A=B=∞,即F(A)=F(B)=1,代入条件④可得p+pm=w2,与p>w2矛盾,所以Q*=0,q*>0不能同时成立。 引理1表明,当制造商面临一个风险供应商和一个提供数量柔性的供应商时,制造商不应该只从提供数量柔性的供应商处订购,这不是最优决策。 (3) (4) 性质1非常直观。下面的定理2给出了制造商只从风险供应商处订货的充要条件。 证明 假设Q*>0,q*=0,由KKT条件①和②,可得λ1=0,λ2≥0,代入KKT条件③,④得: 推论1 当制造商同时向两个供应商订货时,若随机变量x服从[μ1-a1,μ1+a1]的均匀分布,那么制造商向供应商的最优订货量分别为: 求解上述方程组即得推论1。 得证。 性质2 当数量柔性供应商的柔性增加或者其批发价下降,或风险供应商的批发价增加时,制造商同时向两个供应商订货(双源采购)的可能性增加。 性质3 当制造商同时向两个供应商订货时:(1)最优订货量Q*(q*)分别随着销售价、缺货成本的增加而递减(增加);(2)Q*(q*)随着数量柔性供应商的批发价的增加而增加(递减);(3)Q*(q*)随着风险供应商的批发价的增加而递减(增加)。 上述性质可通过对一阶条件求全微分得到。性质3(1)表明当销售价或缺货成本增加时,制造商应该更多的从数量柔性供应商处订购同时减少从风险供应商处的订购量。性质3(2)表明当数量柔性供应商的批发价增加时,制造商应该增加从风险供应商处的订货同时减少从数量柔性供应商处的订货。性质3(3)表明当风险供应商的批发价增加时,制造商应该减少从风险供应商处的订货同时增加从数量柔性供应商处的订货。 2.3 需求随机下制造商的采购策略 当制造商面临的随机需求D,其概率密度函数为g(y),分布函数为G(y),期望为μ2。制造商利润函数为: Π3=-(p+pm-w2)(D-q-xQ)+-(w2-v)(D-(1-β)q-xQ)+-(w1-v)xQ-(w2-v)(1-β)q+(p-v)D, 期望利润函数为: E(Π3)=-(p+pm-w2)E(D-q-xQ)+-(w2-v)E(D-(1-β)q-xQ)+-(w1-v)μ1Q-(w2-v)(1-β)q+(p-v)μ2 (5) 我们首先分析期望利润函数的性质。 定理3 制造商的期望利润E(Π3)是关于Q和q的凹函数。 证明 由(5)式,易得E(D-q-xQ)+和E(D-(1-β)q-xQ)+是关于Q和q的凹函数,-(w1-v)μ1Q和(w2-v)(1-β)q分别是Q和q的线性函数。由于凹函数和线性函数的和函数还是凹函数,所以E(Π3)是关于Q和q的凹函数。 得证。 下面分别求期望利润E(Π3)关于Q和q的一阶导数: (6) 其中I{·}为指示函数,当{·}成立时有I{·}=1,否则I{·}=0。 下面的定理给出了随机需求下的最优订货量。 定理4 当且仅当有λ3,λ4≥0满足下式时,存在最优订货量(Q*,q*)。 (7) 证明 由定理3可知期望利润函数是关于Q和q的凹函数,由KKT条件可以得到最优订货数量Q*和q*。由于λ3,λ4≥0,所以有Q≥0,q≥0。③和④是(7)式的互补松弛条件,因此KKT条件是最优订货量的充分必要条件。 由于(6),(7)式的复杂性,无法得到解析解,我们将通过数值计算讨论最优订货量的性质。 本节分析需求确定和需求随机情况下,随机产出、采购成本和柔性对采购策略和利润的影响。 3.1 需求确定 3.1.1 随机产出的变差系数和柔性对订货量和利润的影响 表1给出了风险供应商产出率的变差系数对制造商最优订货量和利润的影响。Q*随着CV的增加而减小;q*随着CV的增加而增加;E(Π1)随着CV的增加而减少。原因是随着CV的增加,风险供应商相对于数量柔性供应商更加没有优势,制造商将减少从风险供应商处的订购量,同时增加从数量柔性供应商处的订购量,这也将导致制造商的采购成本上升,因此其期望利润将下降。 表1 随机产出的变差系数对最优订货量及利润的影响(需求确定) 表2 柔性参数β对最优订货量及利润的影响 3.1.2 供应商批发价格对订货量的影响 图1和图2反映了需求确定下制造商的最优采购策略是基于数量柔性的双源采购策略时批发价格对制造商订货策略的影响。图1反映了Q*随着风险供应商的批发价格w1的增加而减少,q*随着w1的增加而增加。图2正好与图1相反,表明供应商价格的增加会导致制造商减少对该供应商的订货,这也符合实际情况。 图1 最优订货量关于w1的变化情况 图2 最优订货量关于w2的变化情况 3.1.3 销售价格和缺货成本对订货量和利润的影响 表3反映了最优订货量和利润关于p和pm的变化情况。Q*随着销售价格p的增加而减少,q*随着p的增加而增加,E(Π1)随着p的增加而增加。Q*随着惩罚成本pm的增加而减少,q*随着pm的增加而增加,E(Π1)随着pm的增加而减少。表3说明随着销售价格和惩罚成本的增加,制造商会减少向风险供应商的订货,增加向柔性供应商的订货。因为来自柔性供应商的可靠订货量保证了制造商的利润且避免了损失,这与性质3(1)的理论结果是一致的。 表3 销售价格和缺货成本对最优订货量及利润的影响 3.2 需求随机 假设制造商面临的随机需求服从均匀分布D~U[μ2-a2,μ2+a2],其中μ2=200,a2=25,其他参数设置与3.1节相同。通过数值分析进一步得到需求随机下,随机产出的变差系数、柔性、批发价格、对制造商最优采购策略和利润的影响。 3.2.1 随机产出的变差系数和柔性对订货量和利润的影响 表4和表5分别给出了在需求随机下风险供应商产出率的变差系数、柔性参数β对制造商最优订货量及利润的影响。随机需求下最优订货量Q*和q*以及期望利润的变化情况与需求确定情况一致。这是因为随机需求并没有改变供应端特征(产出率的变差系数、柔性参数)对最优订货量及利润的影响趋势;但是改变了供应端特征对最优订货量及利润的影响大小。对比表1和表4,表2和表5,有如下观察结果: 需求确定下的最优订货量Q*比需求随机下的最优订货量Q*小;需求确定下的最优订货量q*比需求随机下的最优订货量q*大;需求确定下的期望利润E(∏1)比需求随机下的期望利润E(∏1)大。由于需求的随机性增大了供需匹配的难度,使得供需更加不平衡,导致随机需求下的期望利润下降。 表4 随机产出的变差系数对最优订货量及利润的影响(需求随机) 表5 柔性参数β对最优订货量及利润的影响(需求随机) 3.2.2 供应商批发价格对订货量的影响 图3和图4反映了在需求随机下供应商的批发价格对制造商的订货量的影响。图3反映了Q*随着风险供应商的批发价格w1的增加而减少,q*随着w1的增加而增加。图4正好与图3相反,表明供应商批发价格的增加会导致制造商减少对该供应商的订货。 图3 最优订货量关于w1的变化情况 图4 最优订货量关于w2的变化情况 3.2.3 随机需求的变差系数对最优订货量和利润的影响 表6给出了随机需求的变差系数对最优订货量及利润的影响。随着需求的变差系数的增加,最优订货量Q*增加,q*减少,期望利润下降。表6的结果与3.2.1的观察结果类似。随着需求不确定性的增加,制造商从价格更便宜的风险供应商处增加订货来平衡需求,同时减少从数量柔性供应商处的订货,这导致供需匹配更难达到,使得期望利润下降。将表6与表4对比后发现:随机产出的变差系数和随机需求的变差系数增加都降低了制造商的利润,但是对于订货量的影响是相反的:风险供应商的订货量随着随机产出的变差系数的增加而减少,随着随机需求的变差系数的增加而增加;数量柔性供应商的订货量随着随机产出的变差系数的增加而增加,随着随机需求的变差系数的增加而减少。这说明,随机产出带来的风险不同于随机需求带来的风险,管理随机需求的策略不一定能很好的管理随机产出,需要我们仔细的审视。 表6 随机需求的变差系数对最优订货量及利润的影响 本文研究了供应商随机产出时,制造商如何利用数量柔性采购策略管理供应风险的问题。通过理论分析与数值计算,本文得到以下主要结论: (1)成本和柔性对于制造商的采购决策有重要影响,制造商需要在两者之间进行平衡。当数量柔性供应商的柔性增加或者其批发价下降,或风险供应商的批发价增加时,制造商同时向两个供应商订货(双源采购)的可能性增加。 (2)随机产出和随机需求对制造商订货决策的影响是不同的,但是都会降低制造商的期望利润。通常,管理需求风险的策略不一定能管理好供应风险。基于数量柔性合同的双源采购不一定优于单源采购。在一定条件下,基于数量柔性合同的双源采购可以有效的管理供应风险,提高制造商的期望利润。 (3)对于制造商而言,放弃单位成本较低的风险供应商,只从提供数量柔性的供应商处采购,不是最优决策。对于数量柔性供应商而言,提供更多的柔性不一定增加获得的订货量,反而会增加风险供应商的订货量;对风险供应商而言,降低其产出率不确定性,能增加其获得的订货量;对风险供应商和数量柔性供应商而言,给定对手不降价,降低批发价能增加获得的订货量。 [1] Yang W, Wu E. Manufacturing a brand. Available at http://www.amcham-shanghai.org/ [2] Osborne C. Apple cuts supply risk, pits Pegatron vs. Foxconn[2013-5-30].www.zdnet.com/article/apple-supply-risk-pits-pegatron-vs-foxconn/. [3] Agrawal N,Nahmias S. Rationalization of the supplier base in the presense of yield uncertainty[J]. Production and Operations Management, 1997,6(3):291-308. [4] Krause D R,Handfield R B, Tyler B B. The relationships between supplier development, commitment, social capital accumulation and performance improvement[J]. Journal of Operations Management, 2007, 25(2): 528-545. [5] 慕银平, 刘利明. 价格柔性合同下的原材料采购策略及风险分析[J]. 中国管理科学, 2015, 23(3): 108-117. [6] Gupta V, He Bo,Sethi S P. Contingent sourcing under supply disruption and competition[J]. International Journal of Production Research, 2015,53(10): 3006-3027. [7] Guo Shanshan, Zhao Lei, Xu Xiaowei. Impact of supply risks on procurement decisions[J]. Annals of Operations Research, 2013,24(1):1-20. [8] Babich V. Independence of capacity ordering and financial subsidies to risky suppliers[J]. Manufacturing and Service Operations Management, 2010, 12(4): 583-607. [9] 李毅鹏, 马士华. 供求不确定下的通用零部件供应商协同研究[J]. 计算机集成制造系统, 2013,19(12):3184-2192. [10] 陈志明, 陈志祥. 议价的OEM供应链在随机供需下的协调决策[J]. 管理科学学报, 2014,17(5):43-51. [11] Gurnani H, Gerchak Y. Coordination in decentralized assembly systems with uncertain component yields[J]. European Journal of Operational Research, 2007,176(3):1559-1576. [12] Li Tao,Sethi S P, Zhang Jun. Supply diversification with responsive pricing[J]. Production and Operations Management, 2013,22(2): 447-458. [13] Tang S Y,Kouvelis P. Pay-back-revenue-sharing contract in coordinating supply chains with random yield[J]. Production and Operations Management, 2014,23(12): 2089-2102. [14] Chen K B, Yang L.Random yield and coordination mechanisms of a supply chain with emergency backup sourcing[J]. International Journal of Production Research. 2014,52(16): 4747-4767. [15] He Yuanjie, Zhang Jiang. Random yield risk sharing in a two-level supply chain[J]. International Journal of Production Economics, 2008,112 (2):769-781. [16] 郑克俊. 期权契约下易逝品供应链协调[J]. 系统工程学报, 2011, 26(2): 211-215. [17] Tsay A A. The quantity flexibility contract and supplier-customer incentives[J]. Management Science, 1999, 45(10): 1339-1358. [18] Sethi S P, Yan Houmin, Zhang Hanqin. Quantity flexibility contracts: Optimal decisions with information updates[J]. Decision Sciences, 2004, 35(4): 691-712. [19] Tsay A A, Lovejoy W S. Quantity flexibility contracts and supply chain performance[J]. Manufacturing & Service Operations Management, 1999, 1(2): 89-111. [20] Chung W,Talluri S, Narasimhan R. Flexibility or cost saving? Sourcing decisions with two suppliers[J]. Decision Sciences, 2010, 41(3): 623-650. [21] Hu Fei, Lim C C, Lu Zudi. Coordination of supply chains with a flexible ordering policy under yield and demand uncertainty[J]. International Journal of Production Economics, 2013,146(2):686-693. Quantity Flexible Procurement Strategy Under Random Yield HE Bo, ZHANG Xia (School of Economics and Business Administration, Chongqing University, Chongqing 400030.China) Random yield of the upstream supplier is often seen in the semiconductor, electronics and chemical industries, which has a significant negative impact on the downstream manufacturer’s operations. Since the major supplier’s (risky supplier) yield is random, to mitigate supply risk, the manufacturer can procure from an alternative reliable supplier (QF supplier) with quantity flexibility contract. So, the manufacturer faces a problem of how to determine its procurement strategy in the presence of random yield. Using stochastic modelling and optimization, the manufacturer’s optimal procurement decisions are investigated under deterministic and stochastic demand, respectively. The structural properties of optimal solutions are analyzed and the conditions under which the quantity flexibility procurement policy should be used are identified. Furthermore, by theoretical analysis and numerical computations, the effect of random yield, flexibility, wholesale price and demand risk on the procurement decisions are examined. It is found that the higher supply risk and demand risk reduce the manufacturer’s expected profit but have different impacts on the manufacturer’s order decisions. For the QF supplier, it may not obtain more orders by providing larger flexibility to the buyer,on the contrary, doing this may benefit the risky supplier. For the QF supplier or risky supplier, given its competitor’s wholesale price, it can increase its order share by lower wholesale price. Our results can facilitate the manufacturer to mitigate its supply risks. supply uncertainty; yield uncertainty; quantity flexibility contract 1003-207(2017)05-0052-09 10.16381/j.cnki.issn1003-207x.2017.05.007 2015-06-21; 2016-02-14 国家自然科学基金资助项目(71572021);中央高校基本科研业务费(106112016CDJXY020014) 何波(1977-),男(汉族),湖南长沙人,重庆大学经济与工商管理学院,教授,博士生导师,研究方向:物流与供应链管理,E-mail: hebo@cqu.edu.cn. F274 A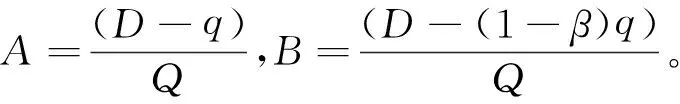









3 数值分析










4 结语
