顾客选择行为对自提点选址的影响研究

陈义友，张 锦，2，罗建强

(1.西南交通大学交通运输与物流学院，四川 成都 610031；2.西安交通大学综合交通运输智能化国家地方联合工程实验室，四川 成都 610031；3.江苏大学管理学院，江苏 镇江 212013)



顾客选择行为对自提点选址的影响研究

陈义友1，张 锦1，2，罗建强3

(1.西南交通大学交通运输与物流学院，四川 成都 610031；2.西安交通大学综合交通运输智能化国家地方联合工程实验室，四川 成都 610031；3.江苏大学管理学院，江苏 镇江 212013)

自提点选址是企业推广顾客自提模式和抢占末端配送市场份额的战略决策之一。与其它物流设施不同，自提点直接面向顾客，顾客可选择是否接受区域中自提点的服务。为使顾客自提量最大化，考虑顾客如何选择目标自提点是至关重要的。为此，考虑顾客取货距离和自提点吸引力等因素，基于竞争选址和逐渐覆盖理论，设计了顾客对自提点的分段效用函数。在此基础上，利用MNL模型和需求弹性函数分别构建了随机选择模型和最优选择模型。为高效地求解模型，设计了免疫算法，并用一个随机算例进行验证。结果显示，顾客选择行为对自提点选址有重要的影响，企业在作决策之前有必要详实地调查顾客的选择行为。

自提点；顾客选择行为；设施选址；效用函数；免疫算法

1 引言

电子商务快速发展催生了快递量的爆发性增长。2014年，全国快递服务企业业务量累计完成139.6亿件，同比增长51.9%。其中“双11”期间(11月11日至16日)，全国共处理快件5.4亿件，同比增长56%；日均最高处理量超过1亿件，同比增长52%。然而快递“最后一公里”配送难题却依然存在。据统计，传统送货上门的快递交付方式一次投递失败比例为12%[1]，易产生二次配送成本，存在法律责任的纠纷，泄露顾客个人信息等问题，而顾客自助提货的方式可以最大限度地降低城市物流系统的交付压力，发挥末端配送的规模效益，同时为顾客提供一种更加柔性化的配送方案。为了提高末端配送的服务质量，国家出台了《关于提升快递末端投递服务水平的指导意见》、《关于促进商贸物流发展的实施意见》等相关政策文件，指出快递企业可尝试开展第三方合作模式，使用智能快件箱；整合存量配送资源，在学校、社区、地铁等周边设立末端配送站或建设公共自助提货柜。各大电商企业、物流企业、第三方企业也纷纷加大对自提点的建设，如京东的校园营业厅、天猫的“阿里小邮局”、顺丰速运的嘿店、速递易的智能快件箱等。

自提点是城乡最后一公里配送的一种空间载体，科学合理地确定自提点的选址方案，可以提高企业末端配送网络的运行效率，增强顾客满意度，扩大企业的市场占有率。自提点选址问题是决策企业从区域范围内选取合适的备选自提点以满足顾客的需求，其区别于其它物流设施诸如物流中心选址的最大特征是直接面向顾客，需求不确定性高，选址时需重点考虑顾客的行为特征。顾客可能是完全理性的，也可能是有限理性的。顾客可依据备选自提点提供的效用，选择接受一个或者多个自提点的服务，或者直接选择送货上门服务。

假设顾客对所有自提点的信息都是完全和准确的，且不存在认知偏差，则顾客每次决策时将选择接受提供最大效用自提点的服务。大部分研究者把这种选择行为称为最优行为(Optimal-choice)。比如，在设施选址理论中，常常假设顾客选择接受距离最近的设施服务。与此相反，假设顾客由于认知偏差及自身能力局限而导致的随机选择行为(Probabilistic-choice)，即顾客以一定的概率接受某个自提点的服务，且选择概率随自提点提供效用的增加而增加。随机选择行为是市场营销和经济学领域常用的选择行为。

值得注意的是，任何一种顾客选择行为是否符合实际取决于具体情况。比如当顾客是老年人或者学生群体且长期居住在某个固定区域时，则适合采用最优选择模型布局物业自提点或者高校自提点。而当顾客是上班族时，顾客可能选择在上班的地方自提货物，或者在回家途中的便利店自提点处提货，或者直接在小区物业自提点提货。可见随机选择模型对于此类顾客更加适用。本文将研究顾客最优选择和随机选择两种行为对自提点选址的影响。

现有关于自提点的研究主要集中在实证分析自提点的开发模式[2-6]、顾客自提选择意愿[7]上，而对于自提点选址的研究较少。McLeod和Cherrett[4]评价了使用地铁站自提点为顾客配送小型包裹产生的环境影响，得出当调查区域20%的顾客使用自提点时可以减少20%的CO排放量和13%～15%的HC、NOX、PM及CO2排放量。Weltevreden[8]借助于快递配送企业日常运营和顾客行为的统计数据，对末端网点作了较为详细而客观地分析，但以定性研究为主。张戎和王镇豪[9]从规划者和客户两个角度出发，建立了城市末端节点的双层规划模型，同时基于反应函数设计启发式算法，求解得到上海徐家汇街道的末端网点布局规划方案。模型的下层规划考虑了末端节点的服务距离、服务价格和服务质量三方面因素，但主要是以成本来衡量，没有考虑顾客的随机选择行为。杨朋珏等[10]综合考虑送货上门和自行取货两种配送模式，建立了基于效率性和便利性的双目标末端网点选址模型，并用遗传算法进行求解，但模型没有考虑顾客到备选网点距离的长短对顾客产生的影响。周翔等[11]考虑配送时长、取货距离和取货时间，以顾客满意度为优化目标，采用中心偏移二次聚类算法求解电商企业末端节点的数量和位置，但模型没有考虑顾客的随机选择行为。顾客在接受自提服务时存在不同选择行为，目前关于顾客选择行为的研究主要集中在设施选址[12-13]、订货决策和产品定价[14-15]等方面。

综上，已有研究成果存在以下问题：(1) 国内外尚未有针对性的、系统的、全面的研究自提点选址问题；(2) 没有深入分析顾客不同选择行为，尤其是顾客随机选择行为对自提点选址的影响；(3) 现有关于顾客选择接受自提点服务的假设前提大都基于距离最短的最优选择，没有考虑自提点的服务水平、服务时间、安全性、沟通便利性等其他影响因素，且距离函数是连续递减，而非分段递减函数。

与本文密切相关的是Zhang Yue等[12]，何波和孟卫东[13]研究，但本文与其存在以下区别：(1) Zhang Yue等研究预防性医疗设施的网络设计问题，何波和孟卫东研究逆向物流网络设计问题，本文研究电商环境下的自提点选址问题；(2) Zhang Yue等以行程时间刻画顾客效用函数，本文考虑顾客取货距离和自提点吸引力等因素，构造分段效用函数；(3) Zhang Yue等运用随机搜索算法和遗传算法求解，何波和孟卫东运用多目标进化算法求解，本文设计免疫算法进行求解；

本文通过借鉴竞争选址和逐渐覆盖理论，重新构造了分段效用函数，在此基础上，用MNL模型刻画顾客随机选择行为，用需求弹性函数分析最优选择行为，研究了顾客两种不同选择行为对自提点选址问题的影响，并针对自提点选址模型特性设计了免疫算法，为电商企业、物流企业或者第三方企业在布局自提点提供科学的决策依据。

2 自提点选址模型

2.1 问题描述

由于消费观念的改变，相比传统的送货上门配送模式，顾客逐渐倾向于灵活自由的自助提货模式，注重自提服务效用的最大化。然而，面对不同的自提点，顾客可以是基于随机选择行为或者最优选择行为接受自提点的服务。如何采用正确的顾客选择行为，建立合适的模型，确定自提点的选址方案，是企业推广顾客自提模式，抢占末端配送市场份额一个亟待解决的问题。

因此本文构建的自提点选址模型描述如下：在给定的网络G(V,A)中，根据顾客随机选择和最优选择行为，依据决策企业需要设立的自提点个数p，在满足自提点预期运营总成本约束条件下，从备选自提点集合J中选择最优的自提点j，使得顾客自提总量最大化。

通过对比分析两种选择模型的最终计算结果，以此探析顾客不同选择行为对自提点选址的影响。

2.2 模型假设

(1) 本文重点研究顾客随机选择行为和最优选择行为对企业布局自提点的影响，因此从单一类型自提点的选址问题着手研究，暂不考虑其它竞争企业对自提点选址的影响；

(2) 尽管自提点处理容量有限，但其在大多数情况下能满足顾客的需求，顾客包裹不会被转移到其他网点，暂不考虑自提点处理容量的限制；

(3) 顾客选择自提点是一个复杂的决策过程，需考虑多种因素，假设顾客选择接受自提点服务的唯一依据是自提点给顾客提供的效用；

(4) 自提作为新兴的配送模式，顾客可能对传统送货上门模式存在依赖心理，故假设顾客需求具有弹性，其需求并非由自提点全部服务。

2.3 模型参数

I表示顾客的集合，∀i∈I；

J表示自提备选点的集合，∀j∈J；

di表示顾客i的初始需求量；

rij表示顾客i到自提备选点j的取货距离；

R表示自提点最大覆盖距离；

r表示自提点最小覆盖距离；

p表示企业设立自提点的个数；

Uij表示顾客i对自提点j的效用；

Aij表示自提点j对顾客i的吸引力因子；

f(rij)表示自提点j对顾客i的距离引力函数；

λ表示顾客的理性程度；

Fj表示自提点j的运营成本；

F表示企业设立自提点的预期运营总成本；

aij表示顾客i接受自提点j服务的概率；

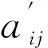
yj取0-1变量，取值为1表示在备选点j设立自提点，否则取值为0。

2.4 模型建立

2.4.1 效用函数

Morganti等[2]通过分析法国现有运营的自提点，认为自提点可达性是企业在城市和农村地区布局自提点网络的重要影响因素。本文用顾客到自提点取货距离的远近来描述自提点可达性，同时借鉴竞争选址理论，考虑自提点吸引力，构造顾客自提服务的分段效用函数。

在竞争选址中，顾客选择设施的效用与设施的吸引力成正比，与距离的幂函数成反比，见式(1):

(1)

其中，Aj表示设施j的吸引力因子，dij表示顾客i到设施j的距离，β表示距离敏感系数。式(1)表明只要设施的覆盖距离足够近，无论设施的吸引力如何变化，顾客的效用都可以达到最大。

然而，顾客选择自提点的偏好由多种因素共同决定，距离只是其中影响因素之一，吸引力大的自提点在一定程度上可以让顾客忽略对距离的影响，如便利店自提点可以吸引顾客在取快递的同时，进行购物，顾客也愿意多走一段路程。由于在自助提货模式下，顾客大多是步行到自提点，取货距离是关键。在本文中，取货距离指的是顾客从平时某一固定场所到自提点的行走距离，如高校学生寝室和自提点之间的距离，或者顾客偏离既定路线到自提点取货的距离，如上班族在回家途中到周边自提点取货的偏离距离。当顾客到自提点的距离超过一定的范围时，距离对顾客效用的影响就逐渐显现出来。Drezner等[16]拓宽了传统“二元”覆盖的局限性，提出采用逐渐覆盖模型可解决基于顾客满意度的选址问题。逐渐覆盖理论从顾客角度出发，认为覆盖度是顾客到设施距离的非增函数，取值范围为[0,1]，而非0或者1。基于逐渐覆盖理论，本文采用凹凸覆盖函数来刻画距离引力函数，见式(2):

(2)

其中ηi为顾客i的距离敏感系数。

在实际的自提点选址中，式(1)的Aj需通过自提点的服务水平、服务时间、安全性、沟通便利性等多种因素计算得到。为便于计算，本文只给出自提点最终吸引力的数值。

尽管式(1)的Aj能描述不同候选设施的区别，但是无法刻画同一设施对不同顾客吸引力的区别。考虑到不同顾客对选择同一设施服务质量的认知偏差，采用Aij来修正Aj。

故顾客i对自提点j的效用函数为:

Uij=Aijf(rij)

(3)

2.4.2 随机选择模型

在设施选址中，顾客随机选择是指每一个顾客是以一定的概率接受设施的服务，选择概率与目标设施提供的效用成比例。在市场营销和经济学领域，常用的模型有Huff模型[17]，MCI模型[18]和MNL模型[19]。其中，MNL模型已成为刻画顾客随机选择行为的一种重要方法[20]，已经被应用到设施的选址-分配上[12]。

基于MNL模型，考虑顾客有可能不接受自提点的服务，选择送货上门的配送服务，令:

(4)

其中，当λ=0时，顾客不能辨别出各个自提备选点和送货上门的区别，按照相同的概率随机选择接受服务；当λ→∞时，顾客以概率1选择完全理性下的最优配送服务。

定义ai0为顾客i不接受任何自提点的服务，即为选择送货上门的概率，则有:

(5)

值得注意的是，式(4)和(5)中的“1”是一个标准化的数值，代表不接受任何自提点服务的效用[21]。这与二类评定模型保持一致，即只有两个可选项(接受或者拒绝)。

给定的网络G(V,A)中，建立基于顾客随机选择的自提点选址模型如下：

(6)

S.t: (2)、(3)、(4)和

(7)

(8)

yj=0,1 ∀j∈J

(9)

问题P1目标函数式(6)表示顾客自提总量最大化；约束式(7)表示设立的自提点运营成本之和不超过企业预期的运营总成本；约束式(8)是保证自提点的数量为p个；约束式(9)是决策变量的0-1约束。

由式(4)的非线性可知，问题P1属于非线性混合整数规划问题。

式(4)可以转换为:

(10)

引入新变量zijk，式(10)可以转换为:

(11)

zijk≤aiji∈I,j∈J,k∈J

(12)

zijk≤M1yki∈I,j∈J,k∈J

(13)

zijk≥aij-M2(1-yk)i∈I,j∈J,k∈J

(14)

zijk≥0i∈I,j∈J,k∈J

(15)

其中M1和M2是两个穷大的正数，在这里，将它们的取值均设为aij的上限值，即为1。

故问题P1可转换为线性混合整数规划问题P2：

(16)

S.t:(2)、(3)、(7)至(9)、(11)至(15)

2.4.3 最优选择模型

(17)

式(17)中τi为顾客i的需求弹性系数，τi的值越大，意味着顾客需求越不具有弹性，τi>0。

为了便于描述最优选择模型，引入新的决策变量xij，有:

给定的网络G(V,A)中，建立基于顾客最优选择的自提点选址模型，其可描述为线性混合整数规划问题，如下：

(18)

s.t:(2)、(3)、(17)和

(19)

(20)

(21)

xij≤yj∀i∈I,i∈J

(22)

yj=0,1 ∀j∈J

(23)

xij=0,1 ∀i∈I,j∈J

(24)

问题P3目标函数式(18)表示顾客自提总量最大化；约束式(19)表示设立的自提点运营成本之和不超过企业预期的运营总成本；约束式(20)是保证自提点的数量为p个；约束式(21)保证每一个顾客只能选择一个自提点接受服务；约束式(22)表示只有设立自提点之后，顾客才能进行自提服务；约束式(23)和(24)表示决策变量的0-1约束。

3 算法设计

尽管问题P2和问题P3均为混合整数规划问题，可直接用MIP求解器，比如Lingo或者GAMS软件求解。但是事实证明，对于大规模的算例，用MIP求解器无法在短时间内获得最优解。

从某种角度看，问题P1和问题P3均可以看做P-中值问题的变形。P-中值问题属于NP难问题，需设计启发式算法来求解，常用的求解算法有遗传算法[23]、变邻域搜索算法[24]、结合割平面邻近点结构和禁忌搜索算法的元启发式算法[25]等。Chun等[26]综合比较了免疫算法与遗传算法、进化策略的区别，得出免疫算法在某些特定优化问题上优于遗传算法和进化策略。汤旻安等[27]将免疫算法中抗体多样性维持机制引入到遗传算法中，构造了免疫遗传算法，并应用到铁路应急供应车站的选址问题中。本文尝试将免疫算法运用到自提点选址问题中，以拓展物流设施选址的求解算法。

免疫算法是受生物免疫系统启发，在免疫学理论基础上发展起来的一种新兴的智能计算方法。其采用群体搜索策略，并强调群体个体间的信息交换，主要经过初始抗体种群产生、评价标准计算、种群间个体信息交换、新抗体种群产生这一个循环过程，最终以较大概率获得问题的最优解。

结合模型的特性，设计免疫算法步骤如下：

步骤1：产生初始抗体群

本文采用简单编码的形式，在可行域内随机产生N个初始抗体。每个选址方案可形成一个长度为p的抗体(p表示设立自提点的数量)，每个抗体代表被选为备选自提点的序号。例如，有20个备选自提点，序号1，2，…，20代表所有自提点的序号，从中选5个作为企业即将设立的自提点。抗体[1 8 9 3 13]代表一个可行解，它表示1，8，9，3，13被选为设立的自提点。这种编码方式可以满足自提点数量约束条件。

步骤2：抗体适应度计算

(1)计算抗体和抗原间亲和力

抗体和抗原间的亲和力用函数AV表示。由于自提点选址问题是最大化问题，故:

(25)

其中，Fv为问题P1和问题P3的目标函数，C表示对违反企业预期运营总成本约束的解给予惩罚，C取一个比较小的正数。

(2)计算抗体和抗体间亲合力

抗体和抗体间亲合力用Sv,s表示。由于抗体的编码方法，各位之间不需要考虑排序，令:

(26)

其中，kv,s表示抗体v和抗体s中相同的位数；L为抗体的长度，等于p。

(3)计算抗体浓度

抗体的浓度用Cv表示，令:

(27)

(4)计算个体期望繁殖概率

个体期望繁殖概率用Pv表示，令:

(28)

其中，α为多样性评价参数，为常数。

步骤3：记忆细胞产生

记忆库的抗体数用δ表示。采取精英保留策略，记精英抗体数为ϑ。则每次产生记忆细胞时，先将与抗原亲和度高的前ϑ个抗体存入记忆库，然后从剩余抗体中选择个体期望繁殖概率高的前(δ-ϑ)个抗体存在记忆库。

步骤4：形成父代群体

父代群体数用N表示。采用记忆细胞产生的方法来形成父代群体。借鉴遗传算法的进化算子，对形成的父代群体进行选择、交叉和变异操作。

(1)选择

抗体被选择的概率等价于式(28)的计算结果。依据抗体被选择概率，采用轮盘赌选择机制进行选择操作。

(2)交叉

依据交叉概率pc，采用单点交叉法进行交叉操作。交叉完产生的新抗体有相同的序号，剔除相同的序号，然后再随机产生新序号，使新抗体的长度等于p。

(3)变异

依据变异概率pm，采用单点变异法进行变异操作。变异完产生的新抗体有相同的序号，剔除相同的序号，然后再随机产生新序号，使新抗体的长度等于p。

步骤5：新抗体群产生

将步骤3产生的记忆细胞和步骤4形成的父代群体合并产生新抗体群。

步骤6：条件判断

是否达到预先规定的最大进化代数MAXGEN，如果达到，则输出结果；否则转向步骤2。

4 算例分析

为了更好地比较随机选择模型和最优选择模型在自提点选址的不同，设计了一个小规模的随机算例进行分析。依据算例数据，采用免疫算法，利用MATLAB R2014a软件，在Inter Core i3-550 @ 3.20 GHz CPU，4.00GB内存电脑上运行计算。

图1和图2为免疫算法求解随机选择模型和最优选择模型的收敛情况。由图1和图2可看出，采用免疫算法求解自提点选址模型，能较快的得到最优解。

图1 免疫算法求解随机选择模型的收敛情况

图2 免疫算法求解最优选择模型的收敛情况

表1和表2为随机选择模型和最优选择模型的分配结果，存在以下区别。

(1)在这个算例中，两种不同选择模型的最终选址结果都有所不同。随机选择模型设立的自提点为[3 4 5 6 7]，顾客自提总量为1645.6131，占初始需求总量的99.9%；而最优选择模型设立的自提点为[3 4 5 6 9]，顾客自提总量为1402.0040，占初始需求总量的85.1%。两种模型的自提总量之所以差距较大，在于受到顾客选择行为，即顾客的理性程度λ和需求弹性系数τi的影响，详细分析见表5和表6。

(2)设立自提点的处理能力有所不同。在随机选择模型下，自提点5处理的自提量(381.8368)大于自提点6处理的自提量(313.9181)；而在最优选择模型下，自提点5处理的自提量(286.8333)却小于自提点6处理的自提量(343.6660)。同样的自提点，在两种不同选择模型下，出现完全相反的两种结果。之所以出现这种不同，在于随机选择模型下，顾客可随机接受每个自提点的服务。对于这个算例中，主要是因为自提点5和自提点6对于顾客12的效用相当，在随机选择模型下，接受自提点5和自提点6的服务，而在最优选择模型下，只接受自提点6的服务。

本文用顾客到自提点距离的远近来描述自提点的可达性，因此自提点的覆盖距离(最小覆盖距离r和最大覆盖距离R)将是衡量顾客选择自提服务的重要选址依据。

由表3和表4可看出，不同的r,R组合，影响最终的选址方案。无论哪种选择行为，自提点覆盖距离越大，设立的自提点服务自提量越大。这并不意味着，自提点的覆盖距离越大越好。较大的覆盖距离要求自提点的处理能力大一点，相应的运营成本也越高。对于企业而言，需要通过实际调研分析明确自提点的覆盖距离。如表3和表4的所示，当r=12，尽管自提点的最大覆盖距离R=16比R=14能服务更多的需求，但是自提量增加幅度并不明显。如果在顾客需求确定情况下，企业可以选择设立r=12,R=14的自提点，而无须设立覆盖距离较大的自提点(r=12,R=16)。

表1 随机选择模型的分配结果

表2 最优选择模型的分配结果

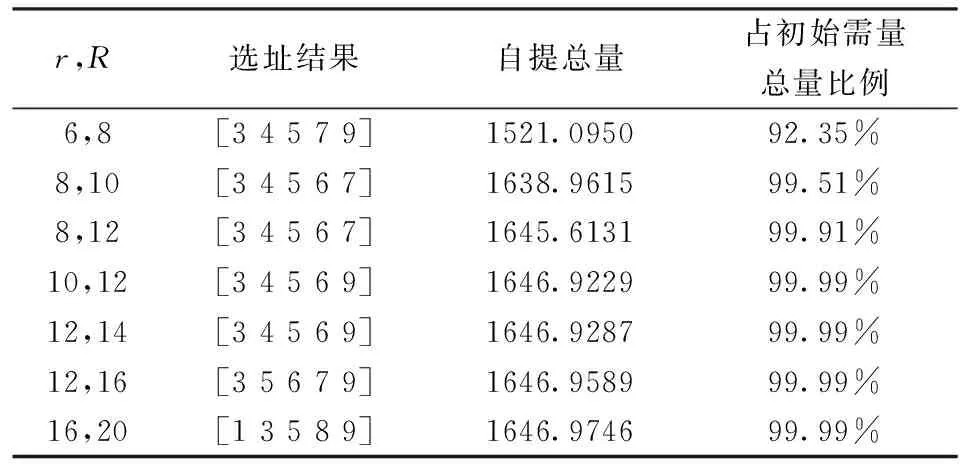
表3 r,R对随机选择模型分配结果的影响

由表5可以看出，在随机选择模型下，λ是一个重要的影响指标，影响着最终选址方案。在给定的算例中，λ的值越大，自提总量也越大。当λ的值取得足够大的时候(这里取λ=100)，随机选择模型的最终选址结果([3 4 5 6 9 ])和最优选择模型一样，但自提总量有可能不一样，原因在于需求弹性系数τi的取值影响最优选择模型的自提总量。

表4 r,R对最优选择模型分配结果的影响

表5 λ对随机选择模型分配结果的影响

为便于分析τi对最优选择模型计算结果的影响，假设所有顾客的τi取值一样，结果如表6所示。在最优选择模型下，τi的取值大小不影响选址结果，但τi的值越大，自提点自提总量也越大。

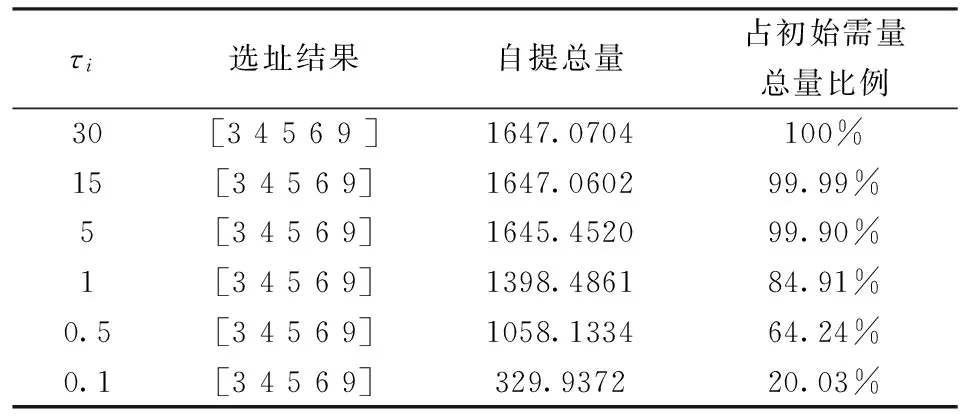
表6 τi对最优选择模型分配结果的影响

5 结语

本文研究的自提点选址问题，考虑了顾客的随机选择和最优选择两种不同行为模式。为了较好地刻画顾客选择接受自提服务的行为，本文借鉴逐渐覆盖的思想，构造了分段形式的距离引力函数，以此来描述自提点的可达性，在此基础上，借鉴竞争选址的理论，修正自提点对顾客的吸引力因子，重新构造了顾客对自提点的效用函数。对于随机选择行为，基于MNL模型，构建了随机选择模型，并引入一个新变量将模型转换成线性混合整数规划问题；对于最优选择行为，基于需求弹性函数，构建了最优选择模型。两个模型均考虑了自提点预期运营总成本约束和自提点个数限制。由于模型属于NP难问题，尤其是对于大规模案例，求解较困难，本文根据模型特性有针对性地设计了免疫算法，算法收敛效果较好。为验证顾客不同选择行为对自提点选址的影响，基于构建的两种选择模型，设计免疫算法，对随机产生的一个算例进行分析。结果显示：(1) 顾客不同选择行为在自提点选址结果、自提总量、自提点处理能力上存在较大差异。企业在布局自提点网络时需充分调查区域内顾客的行为模式，选用合适的选址模型。(2) 自提点覆盖距离越远，顾客自提量越大，但运营成本也越高。为抢占末端配送市场，满足顾客需求，企业可优先与便利店、连锁超市等社会机构合作布局自提点。(3) 顾客理性程度影响选址结果和自提总量，而顾客需求弹性系数对自提总量影响较大。企业在调查顾客的行为模式时，需重点关注顾客理性程度和需求弹性系数两个指标。

针对自提点选址问题，由于不同类型自提点的服务能力和推广难度不一样，应将它们异质化区别，即综合考虑各种因素，分阶段设计不同的自提点网络。此外，在竞争环境中研究已有竞争者对自提点选址的影响。

[1] Roper J, Marsden G. Valuing home delivery-Where's my stuff[M]//Marsden G.Wasted miles, wasted money (a less congested, more energy efficient future).Cambridge:CICC Publications, 2006:53-60.

[2] Morganti E, Dablanc L, Fortin F. Final deliveries for online shopping: The deployment of pickup point networks in urban and suburban areas[J]. Research in Transportation Business & Management, 2014,11:23-31.

[3] Fernie J, Sparks L, McKinnon A C. Retail logistics in the UK: Past, present and future[J]. International Journal of Retail & Distribution Management, 2010,38(11/12):894-914.

[4] McLeod F N, Cherrett T J. Quantifying the environmental benefits of collection/delivery points[J]. OR Insight, 2009,22(3):127-139.

[5] Esper T L, Jensen T D, Turnipseed F L, et al. The last mile: An examination of effects of online retail delivery strategies on consumers[J]. Journal of Business Logistics, 2003,24(2):177-203.

[6] Punakivi M, YrjolaH, Holmstrom J. Solving the last mile issue: Reception box or delivery box?[J]. International Journal of Physical Distribution & Logistics Management, 2001,31(6):427-439.

[7] 徐俊杰, 姜凌, 李亦亮. 基于服务驱动假说的消费者自提包裹选择意愿研究[J]. 管理学报, 2014,11(12):1850-1857.

[8] Weltevreden J W. B2C e-commerce logistics: The rise of collection-and-delivery points in The Netherlands[J]. International Journal of Retail & Distribution Management, 2008,36(8):638-660.

[9] 张戎, 王镇豪. 城市配送末端节点布局双层规划模型及算法[J]. 同济大学学报：自然科学版, 2012,40(7):1035-1040.

[10] 杨朋珏, 胡昊, 王俊嘉, 等. 电子商务环境下城市配送末端网点选址模型研究[J]. 工业工程与管理, 2014,19(01):35-40.

[11] 周翔, 许茂增, 吕奇光. B2C模式下配送中心与末端节点的两阶段布局优化模型[J]. 计算机集成制造系统, 2014,20(12):3140-3149.

[12] Zhang Yue, Berman O, Verter V. The impact of client choice on preventive healthcare facility network design[J]. OR Spectrum, 2012,34(2):349-370.

[13] 何波, 孟卫东. 考虑顾客选择行为的逆向物流网络设计问题研究[J]. 中国管理科学, 2009,17(06):104-108.

[14] 肖勇波, 吴鹏, 王雅兰. 基于顾客选择行为的多质量等级时鲜产品定价策略研究[J]. 中国管理科学, 2010,18(01):58-65.

[15] 徐兵, 熊志建. 基于顾客策略行为和缺货损失的供应链定价与订购决策[J]. 中国管理科学, 2015,23(05):48-55.

[16] Drezner Z, Wesolowsky G O, Drezner T. The gradual covering problem[J]. Naval Research Logistics (NRL), 2004,51(6):841-855.

[17] Huff D L. Defining and estimating a trading area[J].Journal of Marketing,1964,28(3):34-38.

[18] Nakanishi M, Cooper L G. Parameter Estimation for a Multiplicative Competitive Interaction Model: Least Squares Approach[J]. Journal of Marketing Research, 1974,11(3):303-311.

[19] McFadden D. Conditional logit analysis of qualitative choice behavior[M]//Zarembka P. Frontiers in econometrics. New York: Academic Press, 1974:105-142.

[20] Haase K, Müller S. A comparison of linear reformulations for multinomial logit choice probabilities in facility location models[J]. European Journal of Operational Research, 2014,232(3):689-691.

[21] Meyer R J. Context-induced parameter instability in a disaggregate-stochastic model of store choice[J]. Journal of Marketing Research, 1982,19(1):62-71.

[22] Aboolian R, Berman O, Krass D. Competitive facility location model with concave demand[J]. European Journal of Operational Research, 2007,181(2):598-619.

[23] Alp O, Erkut E, Drezner Z. An efficient genetic algorithm for the p-median problem[J]. Annals of Operations Research, 2003,122(1-4):21-42.

[24] Hansen P, MladenoviN. Variable neighborhood search for the p-median[J]. Location Science, 1997,5(4):207-226.

[25] Yaghini M, Karimi M, Rahbar M. A hybrid metaheuristic approach for the capacitated p-median problem[J]. Applied Soft Computing, 2013,13(9):3922-3930.

[26] Chun J, Jung H, Hahn S. A study on comparison of optimization performances between immune algorithm and other heuristic algorithms[J]. IEEE Transactions on Magnetics, 1998,34(5):2972-2975.

[27] 汤旻安, 袁爽, 杨晓晓. 一种求解铁路应急供应车站选址问题的优化算法[J]. 自然灾害学报, 2014,23(04):31-37.

The Impact of Customers’ Choice Behavior on Pickup Point Location

CHEN Yi-you1, ZHANG Jin1,2, LUO Jian-qiang3

(1.School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China；2.National United Engineering Laboratory of Integrated and Intelligent Transportation,Southwest Jiaotong University,Chengdu 610031,China;3.School of Management, Jiangsu University, Zhenjiang 212013, China)

Last mile delivery (LMD) problems have become increasingly prominent with the rapid development of e-commerce. And traditional home delivery service can’t meet customers’ demand. Pickup service provides customers with a more flexible distribution solution, gaining scale benefit of LMD and reducing the delivery pressure of the city logistics system. Pickup point location is a strategic decision for enterprises to broaden customers’ pickup mode and promote market share of LMD. In contrast with other logistics facilities, pickup point is a direct terminal to customers, and customers have a choice in whether to receive service from pickup point in the region or not. In order to maximize the customers’ total pickup demand, it is necessary to put emphasis on how customers choose the pickup points to patronize. To this end, assuming that customers’ pickup distance and pickup points’ attraction are two important attractiveness attributes considered by customers. Based on the competitive location and gradual coverage theory, a piecewise utility function between customer and pickup point is constructed. Under this circumstance, two alternative models are respectively presented with the MNL model and demand elasticity function: in the “probabilistic-choice model”, a customer may patronize each pickup point with a certain probability, which increases with the attractiveness of available pickup point. In contrast, the “optimal-choice model” stipulates that each customer will go to the most attractive pickup point. Both models are formulated as a mixed-integer program. To solve the problems efficiently, an immune algorithm is proposed and a random example is used for verification. The results show that pickup point’s coverage distance, customer rational degree and demand elasticity coefficient affect the location decisions. In particular, the comparison between the two models indicates that the choice behavior of the customer has a significant impact on the pickup point location decisions, and a thorough empirical investigation of this behavior prior to choosing a model is necessary.

pickup point; customers’ choice behavior; facility location; utility function; immune algorithm

1003-207(2017)05-0135-10

10.16381/j.cnki.issn1003-207x.2017.05.016

2015-03-17；

2015-12-29

国家自然科学基金资助项目(71472077，41501123)；四川省软科学项目(2014ZR0032)；中央高校基本科研业务费专项资金资助项目(2682016CX058)

张锦(1963-)，男(汉族)，四川广元人，西安交通大学交通运输与物流学院，教授，博士生导师，研究方向：物流系统规划,E-mail:zhjswjtu@swjtu.edu.cn.

F270;F224.3;C931

A