基于非参数核估计方法的均值-VaR模型

黄金波，李仲飞，丁 杰

(1.广东财经大学金融学院，广东 广州 510320；2.中山大学管理学院，广东 广州 510275)



基于非参数核估计方法的均值-VaR模型

黄金波1，李仲飞2，丁 杰1

(1.广东财经大学金融学院，广东 广州 510320；2.中山大学管理学院，广东 广州 510275)

本文运用非参数核估计方法对资产组合的在险价值 (Value at Risk, VaR)进行估计，得到VaR的非参数核估计公式，并基于VaR的非参数核估计公式建立投资组合选择模型。理论上该模型的目标函数具有良好的光滑性，便于优化问题求解。Monte Carlo模拟结果表明该模型具有大样本性质，估计误差会随着样本容量的增大而下降，且该模型在非对称和厚尾分布下的表现优于当前文献中常用的经验分布法和Cornish-Fisher展开法。基于我国上证50指数及其成份股实际数据的实证结果说明该模型是有效的。

投资组合；在险价值；非参数核估计

1 引言

自Markowitz[1]以收益率的均值和方差反映投资组合的收益和风险，建立均值-方差投资组合优化模型之后，均值-风险权衡模型逐渐成为标准的投资组合分析工具，学者从不同的角度对其进行扩展和完善。而与此同时，针对均值-方差模型，也有来自不同方面的批评，期望收益率作为投资收益的观点已被广泛接受，然而，以收益率的方差作为风险度量指标，受到多方面的质疑，也是受到批评最多的方面。在对方差作为风险度量批评的基础上，发展出了多种风险度量工具，其中，在险价值 (Value at Risk, VaR)是近二十年发展起来的最重要指标。VaR是指在给定置信水平1-α下，在未来特定期间内，资产或资产组合所遭受的最大可能损失。VaR的概念简洁易懂且与人们对风险的心理认知非常接近，成为当前业界最流行的风险度量工具。

VaR在业界的广泛使用激发了学者对基于VaR的投资组合选择问题的研究，在Markowitz的框架内建立均值-VaR模型是研究的重点之一，早期的学者主要在正态分布下对此展开研究[2-6]。显然，正态分布假设与实际金融时间序列数据表现出的尖峰厚尾、非对称等非正态分布特征不符。因此，在不做任何分布假设下，如何准确估计VaR并基于VaR的估计量进行投资决策成为近期研究的热点。CuiXueting等[7]结合Cornish-Fisher展开和Delta-Gamma方法对VaR进行近似计算并建立投资组合模型；CuiXueting等[8]基于经验分布函数建立非参数VaR的资产配置模型，并给出一个新的计算方法。

近年来，许多学者开始运用非参数核估计方法来估计VaR和条件VaR(ConditionalVaR,CVaR)[9-14]，但他们并没有进一步考虑投资组合选择问题。也有一部分学者基于CVaR的非参数核估计公式构建投资组合选择模型，YaoHaixiang等[15]运用非参数核估计方法对CVaR进行估计，并构建了基于CVaR核估计量的投资组合选择模型。黄金波等[16]运用非参数核估计方法得到CVaR的两步核估计量，并基于CVaR的两步核估计量构建投资组合选择模型。由于CVaR是凸风险测度，基于CVaR核估计量的投资组合选择问题是凸优化问题，计算起来比较方便。然而因VaR的非凸性导致基于VaR的优化问题相对较难处理，目前我们还没有发现基于VaR的非参数核估计公式进行投资组合选择问题的研究。因此，本文尝试将VaR的非参数核估计公式嵌入均值-VaR模型，构建基于VaR核估计量的投资组合选择模型。运用MonteCarlo模拟检验该模型的准确性，并基于我国上证50指数及其成份股的实际数据检验该模型的实用性。当前，随着我国金融衍生产品的发展和私募基金的兴起，量化投资已经成为当下业界和学界关注的热点，本文的研究在理论上能够丰富金融工程领域的研究内容，在实践中可为投资者和基金管理者提供新的金融资产配置方法。

2 VaR的非参数核估计

2.1 VaR的定义

假设存在n(n≥2)种风险资产，第i种风险资产的收益率为随机变量ri，则r=(r1,r2,…,rn)′为n种风险资产的收益率向量。记x=(x1,x2,…,xn)′为投资者所持有的投资组合头寸，则组合的收益率R=x′r。根据Jorion[17]的定义，投资组合的VaR是指在给定置信水平1-α和持有期下的最大可能损失，它的数学表达式为：

VaRα(R)=inf{z:Ρrob(-R≥z)≤α}

(1)

即损失超过VaRα(R)的概率小于α，设R的分布函数为F(z)，则上式等价于：

VaRα(R)=inf{z:F(-z)≤α}

(2)

在F(z)满足连续性的条件下，容易得到F(-VaRα(R))=α，从而VaRα(R)=-F-1(α)，即VaR是收益率的逆分布函数的相反数。从定义式来看，要计算VaR，首先要知道分布函数的具体形式，在一些特殊的分布下(如正态分布、t分布等椭球分布)，我们可以得到VaR的解析表达式。但在实际的金融市场中，我们很少能事先知道收益率的分布函数形式，任何事前的分布假设都可能产生模型设定误差。有时即使我们知道分布函数的具体形式，但分布函数中的参数也很难确定。

若r服从n维正态分布N(μ,Σ)，则R服从一维正态分布N(x′μ,x′Σx)，简单推导可知[6]

(3)

z1-α为标准正态分布的1-α分位数。若r服从n维t分布t(μ,Σ,m)，Σ为散度，m为自由度，则R服从一维t分布t(x′μ,x′Σx,m)，此时可得：

(4)

t1-α为经典一维t分布的1-α分位数。一般地，如果r服从n维椭球分布，VaR有如下表达式：

(5)

kκ,α是依赖椭球分布族中某具体分布函数κ和参数α的常数。实际上椭球分布族包含了正态分布、t分布、广义t分布和帕累托分布等，何种分布更适合实际金融市场数据，我们事先并不可知，从而导致kκ,α的选择非常困难；另外椭球分布能够反映出金融时间序列的厚尾性，却不能描述金融时间序列数据的非对称性。

2.2 VaR的核估计量

实际中的金融时间序列数据服从何种分布我们事先并不知道，而非参数核估计方法可以在有限信息的条件下，依赖数据特征来拟合出真实的分布函数，进而可得VaR的核估计量。Chen Songxi和Tang Chengyong[18]证明分布函数的核估计量和经验分布函数都是真实分布函数的一致估计量，但前者的方差更小；并且分布函数的核估计量具有经验分布不具备的连续性和可导性，这些性质在组合优化和风险管理中至关重要，以下给出分布函数的核估计量和VaR的核估计量。

(6)

(7)

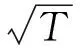
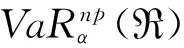
(8)

(9)

限于篇幅，证明略。

3 均值-VaR模型

3.1 均值-VaR建模

在前文基础上，进一步假设市场上不存在卖空限制，资产交易无摩擦，投资者的财富标准化为1。记e是元素全为1的n维列向量，u为投资者要求的最低收益率，则均值-VaR优化模型为：

如果n种资产的收益率服从多维椭球分布，将VaR的解析表达式(5)代入上述优化模型，利用均值-方差模型的组合边界表达式，可以直接得出均值-VaR的组合边界表达式为[6]：

(10)

其中，A=e′Σ-1μ,B=μ′Σ-1μ,C=e′Σ-1e,D=BC-A2。

3.2 核估计框架下均值-VaR模型

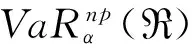
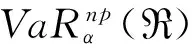
3.3 传统均值-VaR模型

文献中常用的均值-VaR模型主要包括经验分布函数法和Cornish-Fisher展开法。经验分布函数法首先根据组合收益率的样本Rt=x′rt,t=1,2,…,T，得到组合收益率的经验分布函数：

(11)

(12)

基于此，可以构建经验分布函数法下的均值-VaR模型：

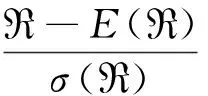
(13)

其中zα为标准正态分布的α分位点。k3和k4分别为R的偏度系数和峰度系数，定义为：

(14)

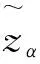
(15)

根据VaR与收益率的分位点之间的关系，可得Cornish-Fisher展开下的VaR表达式为：

(16)

在实际计算中通常利用相应的样本估计式带入(16)式。那么基于样本数据和Cornish-Fisher展开下的均值-VaR模型可写为：

4 模拟分析

本节基于Monte Carlo模拟检验非参数核估计方法下均值-VaR模型的精度，并将其同经验分布函数法和Cornish-Fisher展开法进行比较。考虑到实际金融数据的尖峰厚尾和非对称性，我们分别基于正态分布、t分布和非对称拉普拉斯分布(AsymmetricLaplaceDistribution,ALD)生成随机样本[21-22]，然后将样本数据带入模型Ρ1,Ρ2,Ρ3得到投资组合前沿。为了比较三种估计方法下所得到的组合前沿的精度，我们需要事先知道真实的投资组合前沿曲线的表达式。正态分布和t分布下组合前沿的表达式由(10)式给出，以下引理给出ALD下的真实组合前沿。

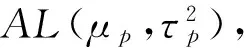
(17)

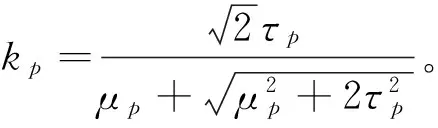
引理2[24]：在ALD下，均值-VaR模型Ρ4等价于以下的优化模型：

根据均值-方差模型的结果，可知模型Ρ5在最优解处的曲线表达式为：

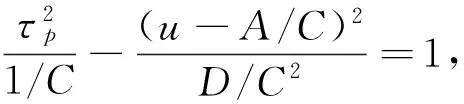
表1 正态分布下的模拟结果

表2 t分布下的模拟结果

表3 ALD下的模拟结果

由于基于VaR的模型是非凸优化问题，迭代算法可能会失败，所以我们记录下N次重复模拟过程中，三种估计方法失败的次数，分别记为K1,K2,K3；如果在某次模拟中，任何一种方法失败，则我们就去掉该次的模拟结果；这样我们定义K4为去掉的模拟次数，那么还剩下M=N-K4次模拟结果，我们基于此定义如下指标来比较三种估计方法的精确度。

AMSEnp,AMSEem,AMSEcf分别代表三种估计方法在M次有效模拟中的平均误差，该指标越小越好。Ratioem代表非参数核估计方法的平均误差与经验分布法平均误差之比，该指标小于1，说明非参数核估计方法更优，反之则反是；Ratiocf的含义与Ratioem类似。Freqem代表在M次有效模拟中，非参数核估计方法的误差大于经验分布法的次数占总次数M的比重，该指标小于0.5，说明非参数核估计方法更优，反之则反是；Freqcf的含义与Freqem类似。为检验三种估计方法的大样本性质，我们取样本容量为T=1000,2000,4000,8000，重复以上过程，模拟结果见表1。为考察厚尾分布和非对称分布下三种估计方法的精度，基于自由度为5的t分布t(μ,Σ,5)和非对称Laplace分布AL(μ,Σ)，重复以上过程，模拟结果见表2和表3。

根据表1-表3，可以得出，在三种不同的分布下，非参数核估计方法的平均误差都小于经验分布法，且从Freqem来看，在M次有效模拟中，非参数核估计方法的误差在绝对多数情况下都小于经验分布法，特别是在样本量比较大时，非参数核估计方法误差大于经验分布法误差的情况为0。与Cornish-Fisher展开法相比，在正态分布和t分布下，非参数核估计方法的平均误差仅在小样本下比Cornish-Fisher展开法小，在样本量较大时，Cornish-Fisher展开法优于非参数核估计方法；这是因为Cornish-Fisher展开法包含了前四阶矩的信息，能够反映分布的厚尾特征；从Freqcf来看，也可以得出在正态分布和t分布下，非参数核估计方法与Cornish-Fisher展开法各有优劣。在既有厚尾又有非对称性的ALD下，无论是从平均误差、平均误差比还是次数占比来看，非参数核估计方法全面占优Cornish-Fisher展开法。另外，从表中也可以看出，非参数核估计方法和Cornish-Fisher展开法具有大样本性质，即估计的平均误差会随着样本容量T的增加而减小，而经验分布法没有表现出这种规律。最后，从三种方法的失败次数来看，非参数核估计方法的失败次数最多，同时，非参数核估计方法的失败次数与样本容量有关，样本容量比较大时，失败的次数会降低，所以非参数核估计方法的精度需要大样本来保证，这也是非参数核估计方法的不足。

为了直观地显示三种估计方法下的投资组合前沿，图1-图3分别给出了小样本(T=500)和大样本(T=8000)下基于三种估计方法所得的组合曲线和真实的投资组合曲线。从图中可以看出，非参数核估计方法和Cornish-Fisher展开法所得到的曲线非常光滑，而经验分布法所得的组合前沿曲线不光滑，这是因为经验分布是组合头寸的不连续函数。此外，从图上可以看出，非参数核估计方法和Cornish-Fisher展开法在大样本下估计误差比小样本下的估计误差更小，而经验分布法没有这种规律。在大样本下，非参数核估计方法在三种分布下的估计曲线都十分接近真实的曲线，而Cornish-Fisher展开法在正态分布和t分布下的估计曲线接近真实曲线，在ALD下基于Cornish-Fisher展开法的估计曲线偏离真实曲线，而且这种偏离不会随着样本容量的增加而减少；这主要是因为Cornish-Fisher展开法是基于泰勒展开仅取前四阶矩的近似计算，当更高阶矩比较重要时，这种近似是存在偏差的。实际中的金融市场数据通常都具有尖峰厚尾和非对称性，此时更适合运用非参数核估计方法。

图1 正态分布下的均值-VaR曲线

图2 t分布下的均值-VaR曲线

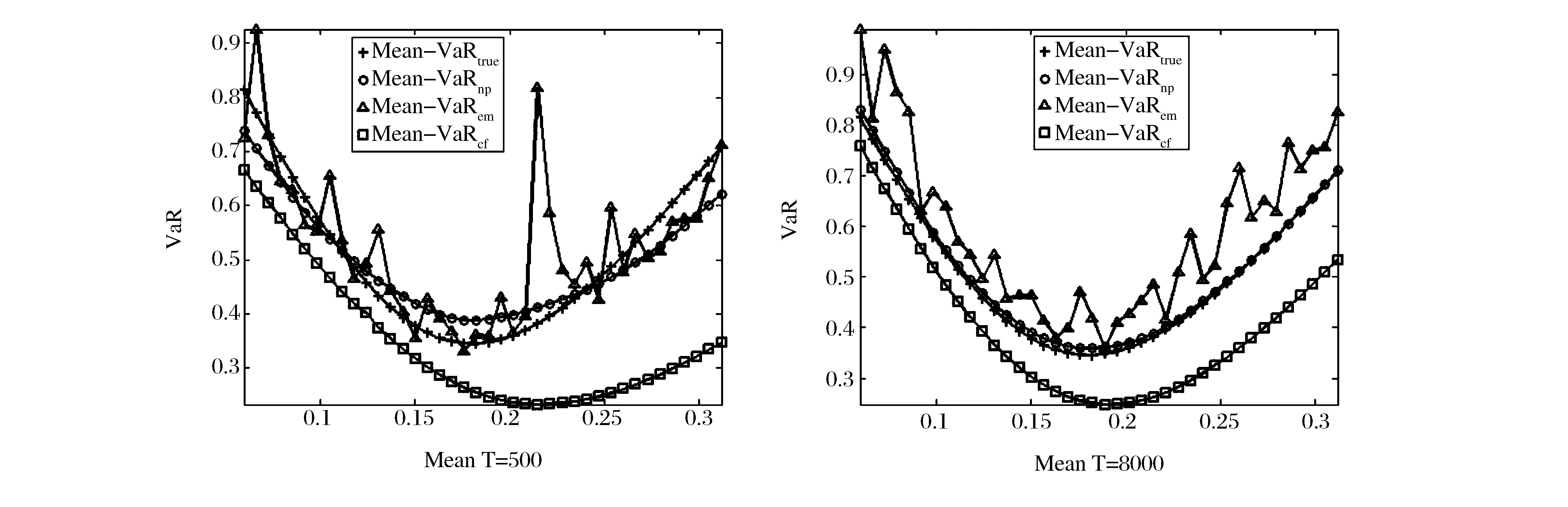
图3 ALD下的均值-VaR曲线

5 实证分析

本节选取我国上证50指数(SSE50)的成份股来进行投资分析，以检验前文建立的非参数核估计框架下的投资组合模型的有效性。我们收集到50支成份股自2004年1月2日至2016年7月8日，共计3040个日收益率数据；同时作为比较基准，我们也收集了上证50指数的日收益率数据，数据来自Wind经济金融数据库。由于日收益率都较小，为了计算方便，所有收益率数据都扩大100倍，即数据的单位为%。我们根据每支成份股的收益率数据和指数收益率数据，计算出每支成份股相对于上证50指数的β值。然后，我们运用上证50指数的部分成份股构造投资组合前沿。由于这50支成份股的收益率服从何种分布，我们事先并不知道，而且数据显示，50支股票收益率数据都具有尖峰厚尾和非对称特征，所以我们无法事先假设一个分布函数的具体形式来进行投资决策，故而，我们运用不需做分布假设的非参数核估计方法、经验分布法和Cornish-Fisher展开法来估计成份股构成的投资组合前沿。我们分别选用β值最接近1的10支成份股和β值最接近1的20支成份股构建投资组合前沿。设定α=5%，取40个不同的投资者要求的最低收益率，基于三种估计方法得到相应的最小VaR，然后在均值-VaR平面用曲线将相应的点连接起来，即得到投资组合边界。三种估计方法下所得到的投资组合边界如图4所示。由图可知，非参数核估计方法和Cornish-Fisher展开法得到的组合前沿比较光滑，而且二者基本一致，而经验分布法得到的投资边界与前两种方法相差很大，而且非常不光滑。另外，相对于10支成份股构成的投资组合边界，20支成份股构成的投资组合前沿有所改善，即在相同均值下，20支成份股构成的投资组合边界处的风险值有所下降。这符合金融学基本原理：增加股票数量会扩大投资者面临的可行集，改善投资策略。

为了进一步检验三种估计方法在实际投资决策中的表现，我们把全样本分成两个子样本，前2000个样本数据作为估计子样本，后1040个数据作为检验子样本。我们首先利用估计子样本的数据得到最优投资策略，然后检验这些策略在检验子样本中的表现，即进行样本外检验。我们基于β值最接近1的10支成份股进行投资决策，利用这10支股票的估计子样本得到非参数核估计方法、经验分布法和Cornish-Fisher展开法下的最优投资策略。然后将这个投资策略运用到样本外，检验这10支股票构成的投资组合的样本外收益。同时，我们分别考虑静态投资策略和动态投资策略。静态投资策略就是运用估计子样本得到最优投资策略之后，在整个检验子样本期间，不再改变资产组合头寸。动态投资策略是适时更新估计子样本，补充最近得到的样本数据，删去离当前时刻较远的历史样本，保证估计子样本的样本容量不变，运用更新的估计子样本，适时调整投资策略。在动态投资策略中，我们每10天更新一次样本，一共进行了104次策略调整。假设初始投资为1元，三种模型下得到的投资策略及上证50指数的累计收益率如图5所示。同时表4总结了投资策略及指数在样本外的收益率均值、方差和夏普比指标。由图5及表4可知：相对于上证50指数，基于非参数核估计方法和Cornish-Fisher展开法的投资策略能够得到更高的平均收益，同时也具有更高的方差，但二者的夏普比都高于指数(见表4)。而基于经验分布法的投资策略表现最差，方差非常大导致其夏普比低于指数。

图4 上证50成份股的投资组合边界(左图：n=10，右图：n=20)

图5 投资策略的样本外表现(n=10，左图：静态策略，右图：动态策略)

指标静态策略(n=10)动态策略(n=10)指数npemcfnpemcfSSE50均值0.07260.04280.06990.06070.06160.05760.0376方差3.85725.12423.45244.26415.77863.97253.1093夏普比0.01880.00840.02020.01420.01070.01450.0121

6 结语

如何对风险测度VaR进行估计一直是风险管理领域的热点话题，其间产生了大量的优秀成果，而如何在准确估计VaR的基础上构建投资组合选择模型是最近提出来的新课题。本文提出非参数核估计框架下的均值-VaR模型，该模型不需要做事前分布假设避免了模型设定误差；虽然该模型不是凸优化问题，但其目标函数仍具有良好的光滑性，便于优化问题的求解；同时该模型具有大样本性质，估计误差会随着样本容量的增加而下降。Monte Carlo模拟结果说明，与传统的经验分布法和Cornish-Fisher展开法相比，非参数核估计法更适合具有尖峰厚尾和非对称性的实际金融市场数据。基于国内上证50指数及其成份股的实证分析说明非参数核估计方法在实际投资决策中是有效的。当然，本文提出的非参数均值-VaR模型也存在以下不足值得进一步研究：首先，该模型需要大量样本才能估计地更为准确；其次，该模型是非凸优化问题，很难找到全局最优解；最后，从Monte Carlo模拟结果可以看出，本文提出的模型有时会失败，特别是当资产数量比较大和样本容量比较小时，该模型可能给不出最优资产配置策略。这些都是后续需要攻克的难题。

[1] Markowitz H. Portfolio selection [J]. The Journal of Finance, 1952, 7(1): 77-91.

[2] Campbell R, Huisman R, Koedijk K. Optimal portfolio selection in a value-at-risk framework [J]. Journal of Banking and Finance,2001, 25(9):1789-1804.

[3] Basak S, Shapiro A. Value-at-risk-based risk management: Optimal policies and asset prices [J]. The Review of Financial Studies,2001, 14(2):371-405.

[4] Alexander G J, Baptista A M. Economic implications of using a Mean-VaR model for portfolio selection: A comparison with Mean-Variance analysis [J]. Journal of Economic Dynamics and Control, 2002, 26(7-8):1159-1193.

[5] Alexander G J, Baptista A M. A comparison of VaR and CVaR constraints on portfolio selection with the Mean-Variance model [J]. Management Science, 2004, 50 (9): 1261-1273.

[6] 姚京, 李仲飞. 基于VaR的金融资产配置模型 [J]. 中国管理科学, 2004, 12(1): 8-14.

[7] Cui Xueting, Zhu Shushang, Sun Xiaoling, et al.Nonlinear portfolio selection using approximate parametric Value-at-Risk [J]. Journal of Banking and Finance, 2013, 37(6): 2124-2139.

[8] Cui Xueting, Sun Xiaoling, Zhu Shushang, et al. Portfolio optimization with nonparametric Value-at-Risk: A block coordinate descent method [R]. Working Paper, 2016.

[9] Cai Zongwu, Wang Xian. Nonparametric estimation of conditional VaR and expected shortfall [J]. Journal of Econometrics, 2008, 147(1): 120-130.

[10] Taylor J W. Estimating value at risk and expected shortfall using expectiles [J]. Journal of Financial Econometrics, 2008, 6(2): 231-252.

[11] Taylor J W. Using exponentially weighted quantile regression to estimate value at risk and expected shortfall [J]. Journal of Financial Econometrics, 2008, 6(3): 382-406.

[12] Alemany R, Bolancé C, Guillén M. A nonparametric approach to calculating value-at-risk [J]. Insurance: Mathematics and Economics, 2013, 52(2): 255-262.

[13] 刘晓倩, 周勇. 加权复合分位数回归方法在动态VaR风险度量中的应用 [J]. 中国管理科学, 2015, 23(6): 1-8.

[14] 黄金波, 李仲飞, 周先波. VaR与CVaR的敏感性凸性及其核估计 [J]. 中国管理科学, 2014, 22(8):1-9.

[15] Yao Haixiang, Li Zhongfei, Lai Yongzeng. Mean-CVaR portfolio selection: A nonparametric estimation framework [J]. Computers and Operations Research, 2013, 40(4): 1014-1022.

[16] 黄金波, 李仲飞, 姚海祥. 基于CVaR两步核估计量的投资组合管理 [J]. 管理科学学报, 2016, 19(5): 114-126.

[17] Jorion P. Value at risk: The new benchmark for managing financial risk [M]. New York: McGraw-Hill, 2007.

[18] Chen Songxi, Tang Chengyong. Nonparametric inference of value-at-risk for dependent financial returns [J]. Journal of Financial Econometrics, 2005, 3(2): 227-255.

[19] Li Qi, Racine J S. Nonparametric econometrics: Theory and practice [M]. Prinseton Princeton University Press, 2007.

[20] Tasche D, Expected shortfall and beyond [J]. Journal of Banking and Finance, 2002, 26(6): 1519-1533.

[21] 杜红军, 王宗军. 基于Asymmetric Laplace分布的金融风险度量 [J]. 中国管理科学, 2013, 21(4): 1-7.

[22] 刘攀, 周若媚. AEPD、AST和ALD分布下金融资产收益率典型事实描述与VaR度量 [J]. 中国管理科学, 2015, 23(2): 21-28.

[23] Kotz S, Kozubowski T, Podgorski K. The Laplace distribution and generalizations: A revisit with applications to communications, economics, engineering, and finance [M]. Berlin:Springer Science & Business Media, 2012.

[24] Zhao Shangmei, Lu Qing, Han Liyan, et al. A mean-CVaR-skewness portfolio optimization model based on asymmetric Laplace distribution [J]. Annals of Operations Research, 2015,226(1): 727-739.

A Mean-VaR Portfolio Selection Model based on Nonparametric Kernel Estimation Method

HUANG Jin-bo1, LI Zhong-fei2, DING Jie1

(1.School of Finance, Guangdong University of Finance & Economics, Guangzhou 510320, China;2.Sun Yat-Sen Business School, Sun Yat-Sen Universtiy, Guangzhou 510275, China)

Value at Risk (VaR), which is widely used by fund companies, banks, securities firms and financial supervision institution, is one of the most popular risk measurement tools presently. The estimation methods of VaR and portfolio optimization models with VaR have been one of the hot spots in recent years. Since VaR is not a convex risk measure, it is difficult to obtain the global optimal solution of portfolio selection problems based on VaR. Moreover, the present study on portfolio selection with VaR is mostly carried out under normal or ellipsoidal distribution assumptions, which is not consistent with the reality of financial markets. In this paper, nonparametric kernel estimation method is firstly applied to estimate VaR and a nonparametric kernel estimator for asset portfolio's value at risk (VaR) is gotten with distribution-free specification. Then kernel estimator of VaR is embedded into the mean-VaR portfolio selection models and accomplish the goal that financial risk estimation and portfolio optimization are implemented at the same time. It is easy to show that the objective function of our model is smooth theoretically and easy to solve the optimization problem. Monte Carlo simulations are carried out to compare the accuracy of our method with the accuracy of classical methods. The simulation results show that our model possesses large sample properties, and outperforms empirical distribution method and Cornish-Fisher expansion method which are usually applied in the classical literatures under the asymmetric and thick tail distribution setting. Finally, our models and methods are applied to the Chinese A stock market. The daily data of SSE 50 Index and its constituent stocks are collected. The data window ranges from January 2nd2004 to July 8th2016, with a total of 3040 daily data. The empirical results show that our model can effectively control risk, as well as obtain excess returns relative to the stock index and support effectiveness of our model and application value of this research. It is acknowledged that, in this study, our nonparametric mean - VaR model has these shortcoming: First, our model requires a large number of samples; Secondly, our model is non-convex optimization problem, which is difficult to find the global optimal solution; Finally, it can be seen from the Monte Carlo simulation, sometimes our model cannot give the optimal asset allocation strategy, especially when the number of assets is large and the sample size is small. These questions are left for further research.

Investment portfolio; Value at Risk; nonparametric kernel estimation

1003-207(2017)05-0001-10

10.16381/j.cnki.issn1003-207x.2017.05.001

2016-07-13；

2017-01-12

国家自然科学基金资助项目(71231008, 71603058, 71573056)；教育部人文社会科学研究项目(16YJC790033)；广东省自然科学基金项目(2016A030313656, 2015A030313629, 2014A030310305)；广东省哲学社会科学规划项目(GD15YYJ06, GD15XYJ03)；广州市哲学社会科学规划项目(15Q20)；广州市社会科学界联合会2016年“羊城青年学人”研究项目(16QNXR08)

李仲飞(1963-)，男(汉族)，内蒙古鄂尔多斯人，中山大学管理学院教授，博士生导师，长江学者，博士，研究方向：金融工程与风险管理，E-mail: lnslzf@mail.sysu.edu.cn.

F830.9

A