GaAs量子阱的自旋扩散特性研究

李博

(山西大学 光电研究所量子光学与光量子器件国家重点实验室,山西 太原 030006;极端光学协同创新中心,山西 太原 030006)

GaAs量子阱的自旋扩散特性研究

李博

(山西大学 光电研究所量子光学与光量子器件国家重点实验室,山西 太原 030006;极端光学协同创新中心,山西 太原 030006)

基于单极自旋扩散方程,建立了(110)-晶向GaAs/(Al,Ga)As量子阱中非平衡态下的自旋扩散模型,并采用有限元方法对模型进行了数值模拟。模拟结果与实验数据的对比显示,在较低激发功率下理论与实验整体符合的很好;而在较高的激发密度,理论和实验分布在短时延处有一定的差异,可能与动态的热载流子效应有关。

量子信息;自旋扩散;有限元方法;二维电子气

0 引言

随着信息技术的进步,传统电子学器件的发展受到诸多制约[1]。量子力学与经典信息科学的结合诞生了包括量子通信和量子计算的量子信息学。经典信息以比特(bits)作为处理单位,用0和1来表示;而量子信息的处理单位是量子比特(qubits),即0和1可以同时存在,每个状态可以用逻辑态0和1的叠加态表示。针对特定算法,量子计算机具有经典计算机难以比拟的强大计算能力[2-3]。实现量子信息处理技术的前提是系统要有好的量子相干性。固态系统如半导体材料中电子自旋具有长的相干时间[4],例如T.Korn小组[5]在(110)-晶向GaAs量子阱(QWs)中观察到了长达100 ns的自旋退相位时间,很适合用作量子信息的载体。实现半导体自旋逻辑器件应用的前提是能对固态系统中自旋的极化注入、存储、操纵、输运和探测进行有效的控制[6-7],同时要求自旋极化系统要有足够长的自旋弛豫时间和足够大的自旋输运长度[8]。

高时空分辨的磁光科尔旋转技术被广泛应用于测量半导体的自旋物理性质,如体材料半导体[9-12]和量子阱[5,13-17]等。凭借其在实空间微区扫描的优势,非常有利于研究半导体的自旋扩散性质:如在n-GaAs体材料中,观察到了数微米[9]至数十微米[10]量级的自旋扩散长度且自旋扩散率受热效应影响[11-12];由于(110)-GaAs QWs具有面外方向的自旋轨道耦合作用,Dyakonov-Perel自旋弛豫机制被完全抑制,因此具有较长的自旋寿命[18];如果(110)-GaAs QWs同时具有较大的自旋扩散率[15],就有机会得到较长的自旋扩散长度[14]。影响(110)-GaAs QWs电子自旋扩散率的因素很多,包括电子迁移率[14-15]、自旋库伦拖拽[19]等材料本身的属性;同时也受到如有效温度以及光学激发密度等[16-17]外界因素的影响。数十微米[13]甚至上百微米[14]的自旋扩散长度已在高迁移率二维电子气(2DEG)系统中观测到。而运用扩散方程来数值模拟电子自旋的扩散行为也在不同的工作中获得了与实验数据比较相符的结果[10,12,15],是描述电子自旋扩散的有效方法。而目前关于低温下激发密度对高迁移率2DEG系统中自旋扩散动力学影响的研究较少,其相应的数值模拟和物理机制也鲜见报道。

本文首先构建了量子阱平面的自旋扩散模型。然后以此模型为研究对象,结合有限元的分析方法,模拟了量子阱平面内电子自旋扩散的动力学过程。通过比较模拟与实验结果,我们观察到了激发密度对自旋扩散动力学的影响并给出了适用于低温下量子阱系统的电子自旋扩散模型。高迁移率二维电子气系统作为场效应晶体管的核心部件具有重要的研究价值;而对该系统中电子自旋扩散动力学过程的数值模拟能够加深人们对其自旋输运性质的理解,有助于自旋晶体管原型器件的实现。

1 样品和实验介绍

本文研究的样品是在(110)-GaAs衬底上用分子束外延技术生长20 nm宽的单GaAs量子阱。样品结构如图1所示,量子阱层夹在100 nm厚的Al0.25Ga0.75As上层和总厚度为100 nm的GaAs/Al0.25Ga0.75As超晶格下层之间,构成一个三明治结构。在距离量子阱中心113 nm处的两侧,均有一定浓度Si掺杂的2 nm厚的GaAs/AlAs单量子阱。由于这种远程掺杂,在20 K的温度下,此电子气系统有高达4.5.×105cm2/Vs的电子迁移率,相应的电子浓度为2.5×1011cm-2。

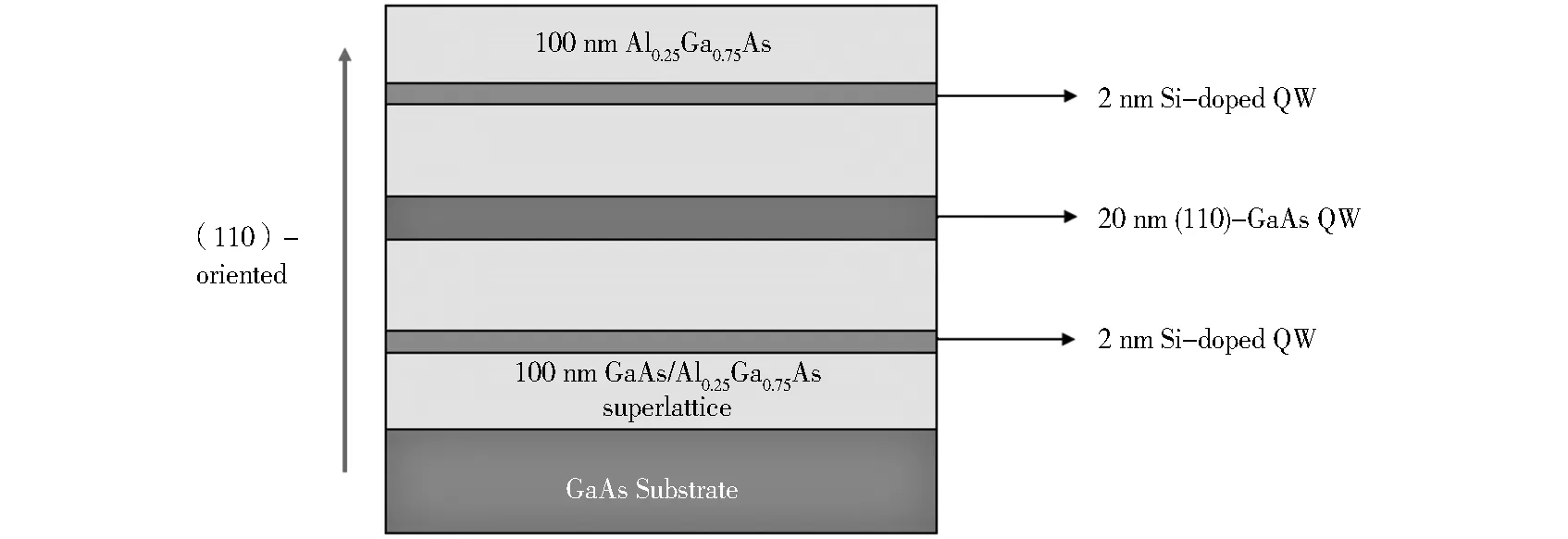
Fig.1 Schematic description of the sample structure图1 样品结构示意图

时间分辨的磁光科尔旋转测量是基于双色泵浦-探测的超快光学技术。实验装置如图2所示,泵浦光和探测光脉冲分别由两台互相同步、重复频率为78.0 MHz的脉冲激光器产生;两者波长分别为790 nm和807.7 nm。用一个电控位移平台控制探测脉冲和泵浦脉冲的相对时间延迟。其中,泵浦脉冲通过光弹调制器在左旋光与右旋光之间调制,调制频率为50.2 kHz;基于光学选择法则,泵浦光通过对GaAs进行带间激发可以产生电子自旋极化[20]。线性偏振态的探测光脉冲通过斩波器调制光强,调制频率为183 Hz。样品被置于低温恒温室内,所有的测量均在20 K的低温下进行。泵浦光和探测光由一个焦距为4 mm的高数值孔径物镜聚焦在样品表面,其高斯光斑束腰半宽约1.1 μm;通过扫描泵浦光的入射角度,实现两束光在空间上的微区扫描测量。探测光经过样品后的反射光经过一个沃拉斯顿棱镜后,其互相正交的偏振分量分别进入两个光电二极管。基于平衡探测和双重锁相技术,我们可以灵敏探测泵浦光所产生的自旋动力学过程。

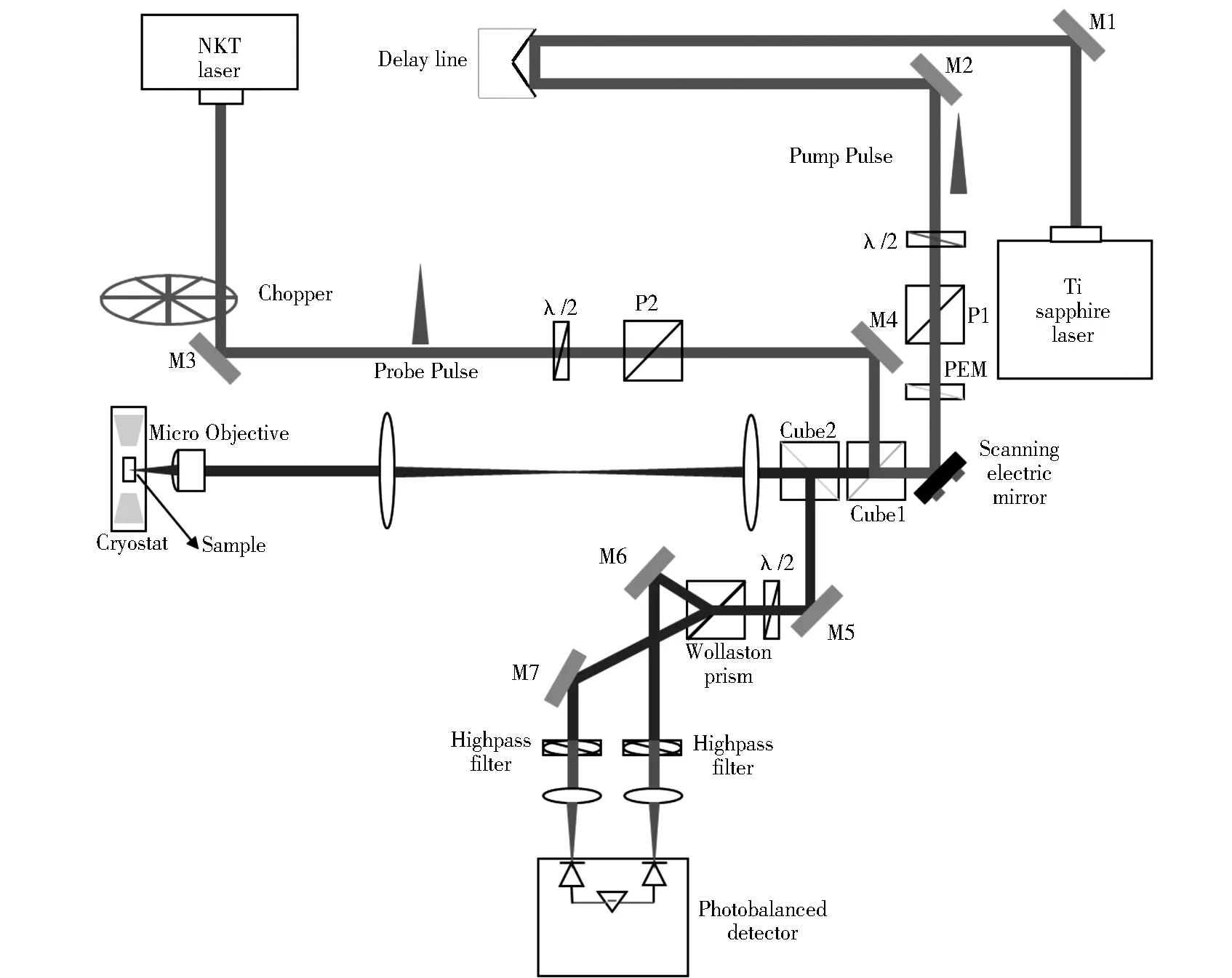
Fig.2 Schematic description of the experimental setup图2 实验装置示意图

2 实验数据拟合结果

图3(a)和3(b)给出了不同延时下的自旋极化分布,实验结果分别在泵浦功率Ppump=20 μW和Ppump=40 μW的实验条件下测得。对图3中的两组实验数据做高斯拟合,拟合结果如图3(a)和3(b)中实线所示。

从图4的拟合结果中我们得到Ppump=20μW和Ppump=40μW对应的自旋扩散率Dsa≈0.021m2/s≈Dsb,相应的初始自旋极化分布标准差分别为σ0a≈0.55μm,σ0b≈0.6μm。

3 自旋扩散模型与模拟结果

基于以上的实验结果,我们用COMSOLMultiphysics软件模拟了电子自旋在量子阱平面的扩散。

应用经典偏微分方程接口中的对流-扩散方程建立一个二维自旋扩散方程,对流-扩散方程的形式如下

(1)

(2)

Fig.3 Spatially resolved and normalized spin polarization at sequential time delay t.Sphere symbols are experimental data for two pump powers:(a)Ppump=20 μW,(b)Ppump=40 μW.Solid lines are fitted by Gaussian distributions球状符号是实验数据,对应于泵浦功率(a)20 μW;(b) 40μW。实线表示对实验结果的高斯拟合图3 不同延时下的归一化自旋极化分布

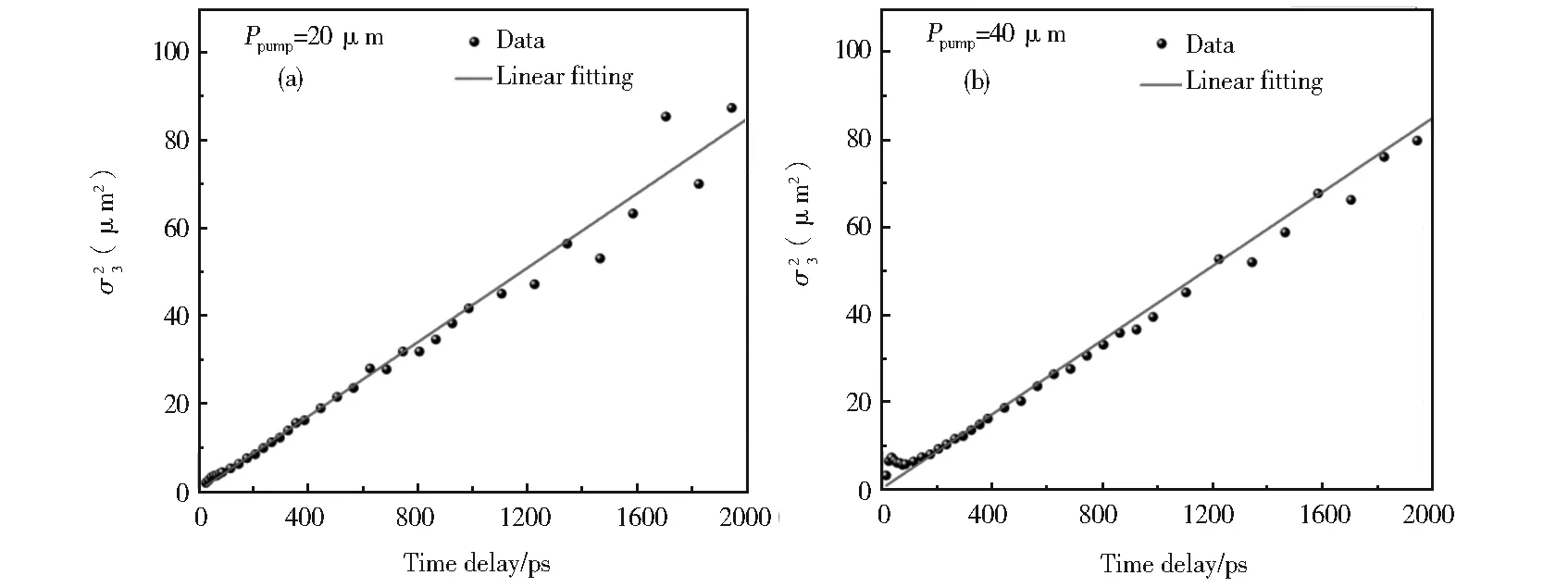
g.3. Sphere symbols are experimental data for pump powers(a)Ppump=20 μW,(b)Ppump=40 μW. Solid lines are linear fits for data球状符号是实验数据,对应于泵浦功率(a)20 μW;(b) 40 μW。实线是相应的线性拟合图4 对图3做拟合得出的关系

研究的量子阱平面大约是3mm×5mm的矩形区域;结合样品的几何尺寸,几何模型用一个半径为220μm的圆来表示。样品和模型空间尺度均远远大于电子的自旋扩散长度(ls≈12μm),在二者边界处,电子自旋极化衰减为0,二者适用的边界条件均为狄氏边界条件。

事实上,由于较长的自旋寿命,实验测得空间分布的自旋极化并不只是单个高斯脉冲作用的结果,而是多个高斯行为的累加,因此初始的自旋极化需要考虑零延时前多个脉冲的影响,在模型中可近似为t=0前第一个脉冲产生的剩余自旋极化。

基于以上的自旋扩散模型,相应的狄氏边界条件和初始条件应该表示如下:

当r→∞时,Sz=0,

(3)

(4)

上式中等号右边第一项代表当前脉冲激发的自旋极化,第二项表示零延时前第一个脉冲激发的剩余自旋极化。r指平面内一点距泵浦光斑中心的距离,σ0是初始自旋极化分布标准差,σ1表示零延时前第一个脉冲产生剩余自旋极化的标准差,Sz,0是激发中心初始(r=0,t=0)自旋极化,A是系数。

将方程(4)代入自旋扩散方程(2)中,可以得到初始自旋极化分布对时间t的微分为:

(5)

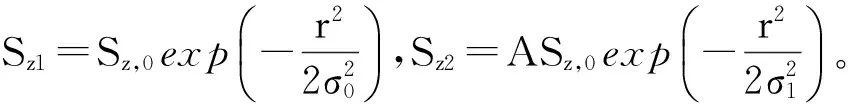
我们运用自旋扩散方程(2)和相应的约束条件(3)-(5)建立了量子阱平面的自旋扩散模型。模拟中需要设置的参数分别是Ds,τs,Sz,0,σ0,σ1和A。

基于有限元分析方法,为了得到更为精确的模拟结果,我们对自旋扩散几何模型做了最大单元尺寸不超过1.5μm的精细三角形网格划分。

对于Ppump=20μW的情形,参数Ds和σ0由实验数据拟合结果确定,即Ds=Dsa≈0.021m2/s,σ0=σ0a≈0.55μm;相关的实验测得T=20K的自旋寿命τs≈7ns[21];考虑到光学方法在量子阱系统中产生的自旋极化率理论上可达到100%[20],取Sz，0=1;σ1=32.7μm由图3(a)中t=25ps的拟合参数给出。通过搜寻参数选取A=0.002 5,得到了与Ppump=20μW的实验结果对应的模拟图像,如图5所示。

Fig.5 Numerically simulated spin diffusions corresponding to experimental data with Ppump=20 μW图5 Ppump=20 μW情形下自旋扩散的数值模拟

由于模型中自旋扩散是各向同性的,因此从图5中观察到了平面对称的自旋极化分布。且随着延时的增加,自旋极化分布轮廓在二维平面内明显地增大,表明了电子自旋在空间上发生了扩散。

在图5中过圆心作一条截线,获得一维的自旋极化分布,如图6(a)实线所示。将其与实验数据做对比,发现二者符合的很好。

Fig.6 Spatially resolved and normalized spin polarization at sequential time delay t.Sphere symbols are experimental data for two pump powers:(a)Ppump=20 μW,(b)Ppump=40 μW. Solid lines are simulation results 球状符号是实验数据,对应于泵浦功率(a)20 μW;(b)40 μW。实线是数值模拟结果图6 不同延时下的归一化自旋极化分布

运用相同的模型对Ppump=40μW的实验结果进行了数值模拟。将图4(b)中拟合得到的参数Dsb=Dsa≈0.021m2/s,σ0=σ0b≈0.6μm和图3(b)中t=25ps的实验数据拟合参数σ1=37.8μm代入到模型中。τs和Sz,0与Ppump=20μW模型参数设置相同,将参数A=0.002 5赋值到模型中,模拟结果如图6(b)实线所示。从图6(b)中可以看出,在最初的延时实验数据和模拟结果有差异,相应的实验结果在短延时的包络宽度要略大于模拟值;这是由于在泵浦光激发后约100ps内,磁光科尔信号除自旋动力学贡献外,还包括动态电子浓度和电子温度二者的影响[22-23]。而随着延时的增加,理论模拟与实验结果趋于一致。

以上模拟结果说明我们建立的自旋扩散模型适用于描述20K下二维电子气系统中电子自旋的扩散行为。

4 结论

本文对20K的低温下泵浦功率分别为20μW和40μW的实验结果做了拟合。根据COMSOLMultiphysics中对流扩散方程建立了二维的自旋扩散方程。结合模型的几何性质,选用第一类边界条件;考虑到较长的自旋寿命,确定了初始条件。运用自旋扩散方程和约束条件构建了二维电子气系统的自旋扩散模型。以实验结果拟合参数为参考,运用有限元分析方法对模型进行了数值模拟。将实验数据与模拟结果作对比,发现在20μW的激发功率下,实验和理论符合的很好;而对于40μW的激发功率,受动态电子浓度和温度的影响,较短延时的实验包络宽度要略大于模拟宽度;在之后的延时范围内,实验和理论结果趋于一致。两组模拟参数非常接近,表明了激发密度的改变对模拟结果的影响局限在短时延范围内。

致谢：我们感谢陈院森的讨论和提供实验数据,此外我们特别感谢IBM-Zurich的G.Salis以及ETHZurich的W.Wegscheider和S.Faelt提供样品。感谢张桐耀、刘晓波和李艳旭参与了论文的讨论。

[1]SarmaSD.ANewClassofDeviceBasedonElectronSpin,RatherThanonCharge,MayYieldtheNextGenerationofMicroelectronics[J].American Scientist,2001,89:516.DOI:10.1511/2001.6.516.

[2]BraunsteinSL,vanLoockP.QuantumInformationwithContinuousVariables[J].Rev Mod Phys,2005,77:513-516.DOI:10.1103/RevModPhys.77.513.

[3]LaddTD,JelezkoF,LaflammeR,et al.QuantumComputers[J].Nature,2010,464:45-46.DOI:10.1038/nature08812.

[4]DiVincenzoDP.ThePhysicalImplementationofQuantumComputation[J].arXiv preprint quant-ph/0002077,2000.DOI:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E.

[5]GriesbeckM,GlazovMM,ShermanEYa,et al.StronglyAnisotropicSpinRelaxationRevealedbyResonantSpinamplificationin(110)GaAsQuantumWells[J].Phys Rev B,2012,85:085313.DOI:https:∥doi.org/10.1103/PhysRevB.85.085313.

[6]WolfSA,AwschalomDD,BuhrmanRA,et al.Spintronics:ASpin-BasedElectronicsVisionfortheFuture[J].Science,2001,294:1488-1490.DOI:10.1126/science.1065389.

[7]AwschalomDD,Flatt’eME.ChallengesforSemiconductorSpintronics[J].Nat Phys,2007,3:153-155.DOI:10.1038/nphys551.

[8]MuraliR.GrapheneNanoelectronics:FromMaterialstoCircuits[M].Berlin:SpringerScience&BusinessMedia,2012：100-101.

[9]CrookerSA,SmithDL.ImagingSpinFlowsinSemiconductorsSubjecttoElectric,Magnetic,andStrainFields[J].Phys Rev Lett,2005,94:236601.DOI:10.1103/PhysRevLett.94.236601.

[10]FurisM,SmithDL,KosS,et al.LocalHanle-effectStudiesofSpinDriftandDiffusioninn:GaAsepilayersandSpin-transportDevices[J].New J Phys,2007,9:347.DOI:10.1088/1367-2630/9/9/347.

[11]HennT,QuastJ-H,BeckM,et al.HotElectronSpinDiffusioninn-typeGaAs[J].Eur Phys J Plus,2014,129:118.DOI: 10.1140/epjp/i2014-14118-y.

[12]HennT,KiesslingT,OssauW,et al.PicosecondReal-spaceImagingofElectronSpinDiffusioninGaAs[J].Phys Rev B,2013,88:195202.DOI: 10.1103/PhysRevB.88.195202.

[13]VölklR,GriesbeckM,TarasenkoSA,et al.SpinDephasingandPhotoinducedSpinDiffusioninaHigh-mobilityTwo-dimensionalElectronSystemEmbeddedinaGaAs-(Al,Ga)AsQuantumwellGrowninthe[110]Direction[J].Phys Rev B,2011,83: 241306.DOI: 10.1103/PhysRevB.83.241306.

[14]VölklR,SchwemmerM,GriesbeckM,et al.SpinPolarization,Dephasing,andPhotoinducedSpinDiffusionin(110)-grownTwo-dimensionalElectronSystems[J].Phys Rev B,2014,89:075424(R).DOI:10.1103/PhysRevB.89.075424.

[15]ChenYS,FältS,WegscheiderW,et al.UnidirectionalSpin-orbitInteractionandSpin-helixStateina(110)-orientedGaAs/(Al,Ga)AsQuantumWell[J].Phys Rev B,2014,90:121304(R).DOI: 10.1103/PhysRevB.90.121304.

[16]HennT,KiesslingT,OssauW,et al.UltrafastSupercontinuumFiber-laserBasedPump-probeScanningMagneto-opticalKerrEffectMicroscopefortheInvestigationofElectronSpinDynamicsinSemiconductorsatCryogenicTemperatureswithPicosecondTimeandMicrometerSpatialResolution[J].Rev Sci Instrum,2013,84:123903.DOI:10.1063/1.4842276.

[17]HennT,KieβlingT,MolenkampLW,et al.TimeandSpatiallyResolvedElectronspinDetectioninSemiconductorHeterostructuresbyMagneto-opticalKerrMicroscopy[J].Phys Status Solidi B,2014,251:1845-1847.DOI:10.1002/pssb.201350192.

[18]OhnoY,TerauchiR,AdachiT,et al.SpinRelaxationinGaAs(110)QuantumWells[J].Phys Rev Lett,1999,83:4196-4199.DOI:10.1103/PhysRevLett.83.4196.

[19]D’AmicoI,VignaleG.CoulombInteractionEffectsinSpin-polarizedTransport[J].Phys Rev B,2002,65:085109.DOI:10.1103/PhysRevB.65.085109.

[20]MeierF,ZakharchenyaBP.OpticalOrientation[M].Amsterdam:ElsevierSciencePublishing,1984:132-133.

[21] 李艳旭.(110)长向GaAs/(Al,Ga)As量子阱中电子自旋动力学测量[D].太原:山西大学,2016:12-13.

[22]KimelAV,BentivegnaF,GridnevVN,et al.Room-temperatureUltrafastCarrierandSpinDynamicsinGaAsprobedbythePhotoinducedmagneto-opticalKerrEffect[J].Phys Rev B,2001,63:235201.DOI:https:∥doi.org/10.1103/PhysRevB.63.235201.

[23]ShahJ.UltrafastSpectroscopyofSemiconductorsandSemiconductorNanostructures[M].Berlin:Springer-VerlagBerlinHeidelberg,1999：151-153.

Investigation on the Spin Diffusion Dynamics in a GaAs Quantum Well

LI Bo

(State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Opto-electronics,Shanxi University,Taiyuan 030006,China;Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China)

Based on a unipolar diffusion equation, a spin diffusion model after non-equilibrium spin excitation is built in a (110)-oriented GaAs/(Al,Ga)As quantum well, for which a numerical simulation is performed by means of finite element method. The simulation results show good consistence with the experimental measurements in the regime of a lower excitation density.The experimental discrepancy is observed at short time delay for a high excitation density, and this may relate to various effects of hot carriers.

quantum information;spin diffusion;finite element method;two-dimensional electron gas

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.02.014

2016-11-13；

2017-02-23

国家自然科学基金(61574087)；山西省基础研究优秀青年基金(2015021002)；山西省回国留学人员科研资助项目(2015-009)

李博(1991-)，男，山西忻州人，硕士研究生，主要研究方向：半导体自旋电子学。E-mail:bo.li.sxu.guangdian@gmail.com

O438

A

0253-2395(2017)02-0293-07