VL1060立式加工中心床身结构优化设计*

2017-05-25郑文标彭晋民

组合机床与自动化加工技术 2017年5期

郑文标，彭晋民

郑文标1，彭晋民2

(1.福州大学机械工程及自动化学院，福州 350108；2.福建工程学院机械与汽车工程学院，福州 350108)

为了解决传统机床设计过程中存在设计周期长、刚度不足和结构笨重等缺陷。文章依据VL1060立式加工中心床身的结构特点，运用有限元法对床身进行动静态分析和结构优化，在满足机床强度的前提下，进行关键设计尺寸的灵敏度分析，对床身性能影响较大的尺寸进行优化取值，选择最佳优化方案。优化结果表明，运用此方法优化后，减轻了床身的重量，床身的刚度和固有频率均有所提高，为以后加工中心床身的设计提供了指导。

床身；有限元法；动静态分析；结构优化

0 引言

床身是立式加工中心最重要的支撑元件，重量占据立式加工中心总重量的20%～30%，其地位可见一般，床身结构特性的好坏直接影响到机床的加工质量和加工精度，因此，如何控制好床身的结构振动特性是设计人员面临的主要技术难题之一[1]。近年来国内外的科研工作者对床身的振动特性和结构优化做了不少的研究与尝试。徐燕申等运用元结构的方法对床身的结构优化做了有益的尝试[2]；L. Kroll等研究了床身质量对机床能效的影响[3]；汤文成等研究了床身筋板的布局对机床刚度的影响[4]，提出了几种优化方案；陈叶林等利用遗传算法对床身横隔板的间距做了优化，提高了床身的振动特性[5]。这些科研人员的工作均为床身的结构优化设计提供了很好的指导，但上述研究均以床身局部结构或单个性能作为优化目标，并没有对床身的综合性能做系统性的优化。

本文以VL1060 立式加工中心床身为研究对象，运用结构优化设计技术分别对床身进行动、静态分析、灵敏度分析及设计尺寸优化取值，在满足强度的前提下，减轻了床身的重量，动静态性能也得到不同程度的提高。较大程度的节省了机床制造过程中的材料消耗，降低了生产成本，缩短了新产品的设计周期。

1 建立床身有限元模型

1.1 床身模型简化

VL1060立式加工中心床身模型结构较为复杂，有大量细小的螺栓孔、倒角、圆角等。如果对床身模型不做简化，网格划分时在小孔、倒圆角等处会出现许多细小的甚至畸变的网格，加大了计算的复杂度和时间[6]。因此必须对床身做适当的简化，具体的方法是：①去除细小的螺栓孔；②忽略不影响整体结构的倒角、圆角。简化后的床身结构如图1所示。

图1 床身简化后模型

1.2 床身网格划分

按照工程要求，床身的材料设置为灰铸铁，由于床身结构比较复杂，因此采用四面体网格划分[7]。在ANSYS Workbench输入相关物理参数后进行网格划分，得到模型的单元数为253951，节点数为456519，床身的网格划分模型如图2所示。

图2 床身结构网格划分

2 床身静力学分析

VL1060立式加工中心由于机内配置机械手，在加工过程中，如果床身的刚度不足，会更加影响工件的加工精度，因此要求设计人员通过结构优化设计来提高床身的刚度，减小床身的变形[8]。由于立柱、主轴箱以及安装在立柱上的机械手总质量约为1436kg,所以在床身与立柱接触面的Z方向上施加14072N的均布面力，在床身与滑鞍接触面的X、Y、Z方向上施加527N、782N、9600N的均布面力，以此来模拟床身在实际工作中所承受的载荷。本文主要考虑床身的位移与应力问题，因此在ANSYS Workbench中选择变形和应力选项进行计算分析，通过求解，位移和应力云图如图3、图4所示。

图3 床身位移云图

图4 床身应力云图

从应力云图可知，床身的最大应力出现在床身与滑鞍座的接触部位，最大应力为5.9133MPa，此处床身与滑鞍座通过滑块连接的，因此可增大接触面积等方法来缓解此处的最大应力。

从床身的位移云图可知，在此工况下，最大位移同样出现在床身与滑鞍座的接触部位，最大位移量为0.008783mm，主要原因是刀具上的切削力通过工作台和滑鞍传递到床身上，且工作台和滑鞍的重量高达1350kg，因此，为了提高床身的刚度，床身结构还有待优化。

3 床身模态分析

机床的床身是一个多自由度组成的线性系统，它对激励力的响应可看作是在自由状态下固有频率和振型参数组成的各阶模态振型的叠加[9]。模态分析是借助振动系统的模态参数来对机械结构的动态性能进行分析、评价、预测和优化的方法，也是确定机械结构薄弱环节的有效方法。

由于床身的固有频率在模态分析中与外界载荷、运动状态无关，且床身通过地脚螺栓固定在地基上，因此在ANSYS Workbench中只需对床身的底面施加固定约束，经过求解，得到床身的前6阶固有频率和振型。由于篇幅所限，本文只列出床身的前3阶振型图，如图5所示，其固有频率值和振型分析如表1所示。

(a)1阶模态振型

(b)2阶模态振型

阶数频率(Hz)振型描述1119.02床身前端上下摆动2196.31床身前端左右摆动3250.93床身绕Z扭转4309.95床身中部上下摆动5372.84床身中部左右摆动6406.21床身上下摆动,并绕Z轴扭转

根据模态分析结果，可以识别床身的振动形态和固有频率等模态参数，找出薄弱环节。在实际应用中，应积极避开其固有频率或减少对这些频率的外界激励，防止共振所造成的破坏；借助振动形态，设计人员可有针对性的加强床身的局部结构，为床身的结构优化设计提供指导。

从图5和表1可以看出，床身的前2阶固有频率均在200Hz以下，需要对其重点分析。另外，床身的振型多为中部、前端的摆动和扭转，说明床身在中间部分和前端的刚度不是很好，这将影响机床的加工精度和稳定性，因此，有必要对床身的结构进行优化设计，提高床身的低阶固有频率，尤其是1阶固有频率。由床身的结构特性分析，本文拟对床身的筋板厚度与壁厚进行尺寸优化。

4 床身结构优化设计

结构优化设计的主要目标是保证模型在约束条件的前提下，尽可能使结构变形小、质量轻，外形合理、强度和刚度好。灵敏度分析能很好的确定设计尺寸参数对目标函数(质量、变形和固有频率)的影响程度，从而找出影响较大的设计尺寸参数，并对其进行重点优化[10]。

4.1 设计尺寸参数的灵敏度分析

VL1060床身的内部均匀布置着8根横向筋板、2根纵向斜筋板，根据床身的结构特点以及动静态分析的结果，适于对床身的筋板厚度与壁厚进行尺寸优化。设计尺寸如图6所示，初始值与变化范围如表2所示。

其中，P1为横向筋板的厚度，P2为纵向斜筋板的厚度，P3为床身前后的壁厚，P4为床身左右两侧的壁厚。

图6 选定的设计尺寸

尺寸初值(mm)变化范围(mm)P11610～22P21610～22P31812～26P42014～28

定义好设计尺寸的初始值和变化范围后，即可在ANSYS Workbench中分析4个设计尺寸对质量、变形和1阶固有频率的影响程度，其灵敏度图如图7～图9所示。

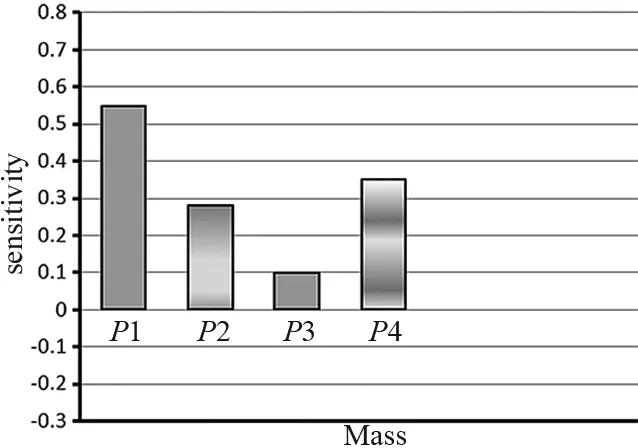
图7 质量灵敏度图

图8 位移灵敏度图

图9 一阶固有频率灵敏度图

通过灵敏度分析可知，横向筋板的厚度P1对床身的质量、位移影响最大；床身左右两侧的壁厚P4对质量、位移的影响次之；纵向斜筋板的厚度P2、前后壁厚P3对质量、位移的影响相对较小；而P1与P4对一阶固有频率的影响很大，P2与P3的影响次之。综上所述，设计尺寸P1与P4对床身性能的影响最大，需要重点优化；由于P2与P3对床身的性能有一定影响，因此保留这2个设计尺寸作为优化参数。

4.2 床身尺寸优化及结果分析

由于优化目标是希望床身的质量、变形减小，1阶固有频率增大，但主要目标是减轻床身的质量，因此在ANSYS Workbench中需对目标函数设置优先级，将床身的质量设置为“High”，床身的变形设置为“Default”，床身的1阶固有频率设置为“Lower”。通过迭代计算，根据优先级的高低筛选出一组最优设计尺寸，并进行圆整，如表3所示。

表3 设计尺寸优化前后比较

根据优化后的设计尺寸，重新建立床身的有限元模型，并在相同的工况下对床身进行静力学与模态分析，优化后的位移云图与1阶振型云图如图10、图11所示，床身优化前后结果比较如表4所示。

图10 优化后床身位移云图

图11 优化后床身1阶振型云图

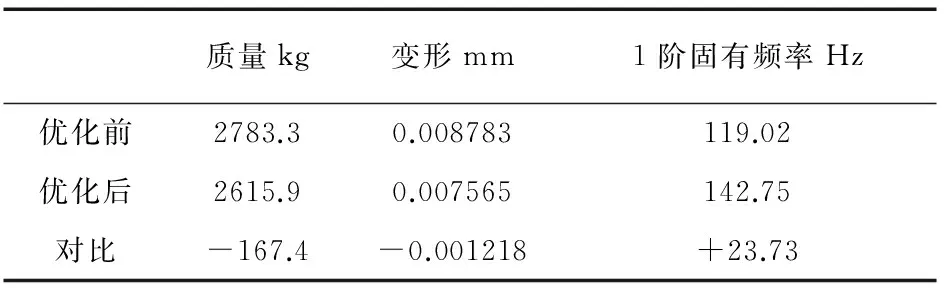
质量kg变形mm1阶固有频率Hz优化前2783.30.008783119.02优化后2615.90.007565142.75对比-167.4-0.001218+23.73

通过分析可知，优化后床身的质量比优化前减轻了167.4kg，降低了生产成本；床身的变形减小了0.001218mm，提高了床身的刚度；1阶模态频率提高了23.73Hz，提高了床身的抗振能力；达到了床身优化设计的预期目标。

5 结论

(1)本文通过对VL1060立式加工中心床身的有

限元分析，得到了床身的位移云图、应力云图、前6阶振型和固有频率，找出床身的薄弱环节，为床身的结构优化设计提供依据。

(2)通过对床身的筋板厚度与壁厚进行灵敏度分析，研究了设计尺寸对床身质量、变形，1阶固有频率的影响程度，对影响程度较大的设计尺寸进行了重点优化，改进了床身的结构。

(3)比较床身优化前后的结构特性，减轻了床身的重量，刚度和1阶固有频率均有所提高，优化效果明显，并可推广到机床的其它部件中，为机床的优化设计提供一定的理论基础。

[1] 丛明，房波，周孜亮. 车-车拉数控机床拖板有限元分析及优化设计[J]. 中国机械工程，2008,19(2)：208-213.

[2] 徐燕申，张兴朝，牛占文,等. 基于元结构和框架优选的数控机床床身结构动态设计研究[J].机械强度，2001,23(1)：001-003.

[3] L Kroll, P Blau, M Wabner, et al. Lightweight components for energy-efficient machine tools [J]. Journal of Manufacturing Science and Technology, 2011(4)：148-160.

[4] 汤文成，易红，唐寅. 机床大件结构的拓扑优化设计[J]. 东南大学学报，1996,26(5)：22-26.

[5] 陈叶林，丁晓红，郭春星,等. 机床床身结构优化设计方法[J]. 机械设计，2010,27(8)：65-68.

[6] 周孜亮，王贵飞，丛明. 基于ANSYS Workbench的主轴箱有限元分析及优化设计[J]. 组合机床与自动化加工技术，2012(3)：17-20.

[7] 孙守林，董慧敏，刘建栋,等. 斜床身卧式车床床身结构轻量化设计研究[J]. 组合机床与自动化加工技术，2015(4)：10-14.

[8] 王万金，殷国富，胡腾,等. 机床多截面拓扑优化方法研究[J]. 组合机床与自动化加工技术，2014(12)：5-9.

[9] 邢俏芳. 机床支撑件元结构设计方法[D]. 大连：大连理工大学，2013.

[10] 杨勇，张为民，李鹏忠. 基于动态灵敏度分析的数控机床床身结构优化设计[J]. 机械设计，2011,28(9)：49-52.

(编辑李秀敏)

Structure Optimization of the Bed on VL1060 Vertical Machine Center

ZHENG Wen-biao1，PENG Jin-min2

(1. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108，China；2. School of Mechanical and Automotive Engineering, Fujian University of Technology, Fuzhou 350108, China)

In order to solve the problem of long design period, insufficient stiffness, heavy structure and other defects in the process of the traditional machine tool design. According to the structure features of the VL1060 vertical machine center, finite element method was used for the static and dynamic analysis and structure optimization of MC bed. Premise to meet intensity of machine, analysis of sensitivity of the key design dimensions. To choose the best optimization scheme by select the dimensions which had most influence on the MC bed. It’s proved that the weight of the optimized bed is reduced、the stiffness and natural frequency were enhanced, providing reference for future structural design of MC bed.

bed; finite element method; static and dynamic analysis; structural optimization

1001-2265(2017)05-0126-04

10.13462/j.cnki.mmtamt.2017.05.033

2016-08-11；

2016-09-22

福建省高校产学合作项目“面向3C产品制造配置机内机器人的智能钻铣加工中心研发”(2017H6002)；福建省科技创新平台建设项目(2014H202);福建省高校新世纪优秀人才项目(JA13207)

郑文标(1990—)，男，福建龙岩人，福州大学硕士研究生，研究方向为机床结构优化、数字化设计，(E-mail)2209992507@qq.com。

TH122；TG65