基于差分插补原理的圆柱插补模式研究

王宏甲，赵庆志，杨召彬

(山东理工大学 机械工程学院，山东 淄博 255000)

基于差分插补原理的圆柱插补模式研究

王宏甲，赵庆志，杨召彬

(山东理工大学 机械工程学院，山东 淄博 255000)

为了实现圆柱表面二次曲线的直接插补，通过对车铣复合加工中心的圆柱插补模式进行分析，提出将差分插补原理应用到圆柱插补模式中。为了得到圆柱表面插补与平面插补之间的关系，实现圆柱面二次曲线的差分插补，对圆柱面的展开进行了数学分析。通过引进圆柱插补模式缩放比例因子，实现了圆柱插补与平面插补的统一，提高了数控程序的编制与加工效率。经过分析二次曲线差分插补代码，定义了圆柱插补模式的命令格式，并进行了相关的实验验证。实验结果表明，基于差分插补原理的圆柱插补模式实现了圆柱表面二次曲线的直接插补，并且易于理解与编程。

差分插补原理；圆柱插补模式；旋转轴；二次曲线

0 引言

圆柱零件是各种机械中常见的重要零件之一。随着机械设计与数控技术的快速发展，对于圆柱面轮廓曲线加工的需求也日益强烈[1]。比如，圆柱槽凸轮的加工以及圆柱面的汉字雕刻等。因此对圆柱插补模式的研究具有重要的应用价值[2]。

实现圆柱面上轮廓曲线的铣削加工方法主要有CAD/CAM软件自动编程[3]、编制宏程序指令[4-6]以及圆柱插补指令[7-9]。其中CAD/CAM自动编程采用微小直线或圆弧对非圆二次曲线进行拟合，程序极为复杂，加工效率比较低[10]。编制宏程序指令需要进行复杂的数学运算，对于非圆二次曲线的加工没有统一的编程标准，降低了生产效率和加工精度。圆柱插补指令主要是在圆柱面展开的状态下进行程序编写，编程方便，易于掌握。但是，圆柱插补指令同样无法对非圆二次曲线进行直接插补，并且该功能主要应用在比较高档的车铣复合加工中心，普通的经济型数控机床一般无此功能。

针对上述情况，本文通过对车铣复合加工中心的圆柱插补模式进行分析与参考，提出采用差分插补原理[11]在第四轴上实现圆柱面轮廓曲线的插补，以期在普通的经济型数控机床上实现易于编程且能够直接插补二次曲线的圆柱插补模式。

1 车铣加工中心的圆柱插补模式分析

1.1 圆柱插补模式的定义

通过文献[7-9]可知，车铣复合加工中心的圆柱插补模式是指将以角度指定的旋转轴转动量，先根据圆柱的直径变换成相应圆周上直线轴的移动量，用该移动量与其他轴进行直线或者圆弧插补。插补后再逆变成旋转轴的转动量，控制旋转轴进行插补运动。

1.2 圆柱插补模式的插补精度

圆柱插补模式对旋转轴的旋转量进行内部换算成移动量后，由插补结果再逆变为旋转量。在这一转换过程中，移动量的舍入为一个最小输入增量单位。实际转动量的计算公式，如下式所示。

其中：

MOTION REV：回转轴每转的移动量

R：工件半径

[]：舍入至最小输入增量单位

由上式可知，在执行转换时，转动量按照输入的最小增值进行。当圆柱体半径比较小时，实际的转动量与指定的转动量不等。不过，这一误差不会积累[7]。

1.3 圆柱插补模式的优缺点

在车铣复合加工中心的圆柱插补模式下，圆柱凸轮槽这一类型零件的加工程序能够非常容易地编制，实用价值非常高[2]。但是，随着工程应用对机械产品性能以及外观要求的不断提高，在圆柱外表面加工的曲线轮廓出现了更高的要求，比如雕刻汉字以及加工常见的二次曲线等。如若在车铣复合加工中心的圆柱插补模式下进行上述加工，需对大量的坐标点进行计算，二次曲线的加工一般只能采取曲线拟合的方式进行，工作量很大，加工效率比较低[3,7]。

2 旋转轴插补编程的数学理论基础

本文采用车铣复合加工中心圆柱插补模式的基本思路，在三坐标数控雕刻机中，增加第四轴(旋转轴)来实现基于差分插补原理的圆柱插补模式。在加工的过程中，将原来的移动轴用旋转轴替代，用旋转轴的转动将所加工的轮廓曲线缠绕到圆柱外表面。

经上述分析可知，旋转轴与原直线轴之间的数学关系，是联系圆柱面插补与平面插补的重要纽带[4]。本文以加工圆柱面上的圆弧为例，进行数学关系的分析。圆柱面加工圆弧及其展开图，如图1所示。

图1 圆柱外表面加工圆弧及其展开图

分析：由数控系统的插补原理可知，X、Z轴不动时，Y轴每走一个脉冲当量ΔY,B轴如果也联动一脉冲当量ΔB，只需要给定ΔY与ΔB的函数关系ΔY=f(ΔB)，则刀具在圆柱表面的运动轨迹就是一确定的轨迹。在对该函数关系式表达的轮廓曲线插补之前，还必须找到ΔB与ΔX的关系，才能实现从直线轴到旋转轴的变换，为实现基于差分插补原理的圆柱插补模式做好数据准备工作。

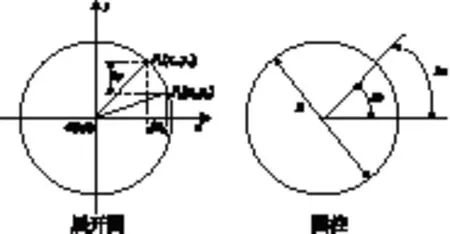
图2 旋转轴与直线轴的数学关系图

如图2所示，在圆柱展开图中，设圆弧半径为R，x轴的增量为Δx，y轴的增量为Δy，圆弧起点为Ps(xs,ys)，圆弧终点坐标为Pe(xe,ye)，圆弧中心为坐标原点O(0,0)，在直径为D的圆柱工件表面上，Δx对应的圆心角为Δb。则Δx、Δb以及工件直径D之间有如下的数学关系：

(2)

由式(2)可得，ΔX、ΔB以及工件直径D之间有如下的数学关系：

(3)

至此，ΔY=f(ΔB)的函数关系已经确定。接下来，下文将把这些函数关系应用到差分插补原理中，实现圆柱面上二次曲线的直接插补。

3 基于差分插补原理的圆柱插补模式

3.1 差分插补原理中的相关概念与定义

3.1.1 差分插补原理的依据与各坐标系的定义

从相关文献[11-12]中分析可得，差分插补原理的依据是从原点开始，依据函数递增的趋势进行推导。在插补的过程中，为满足该插补方法的理论依据，建立了一系列的坐标系。各坐标系的论述如下。

(1)定义用绝对坐标系：该坐标系与通常定义的平面直角坐标系相同，主要用于定义曲线，为数控编程的ISO代码提供与曲线函数相关的加工信息。

(2)相对坐标系：为了保证曲线在加工过程中满足差分插补的理论依据，曲线方程要经过坐标系平移和变向化为可分离变量的正高次曲线。此时会建立相对坐标系，保证曲线起点为坐标原点，起点处的切线在相对坐标系的第一象限。根据可分离变量的正高次曲线，求出x、y的各阶差分。

(3)加工用绝对坐标系：在初始化插补参数时，L为曲线起点的切线方向所在的绝对象限号，象限的定义为L41，L42，L43以及L44。在此绝对坐标系中，x′轴与y′轴的正方向是根据机床进给的正方向选取的。故将其命名为加工用绝对坐标系，为机床各轴进给方向提供基准。在本文中，取x′轴水平向右，y′轴垂直向上为正方向，选取曲线加工起点为坐标原点来建立加工用绝对坐标系。

3.1.2 二次曲线差分插补代码的初始化

将在定义用绝对坐标系中的二次多项式曲线方程Pn(x)=Qm(y)，按照坐标平移和坐标轴变向化为相对坐标系中的正二次曲线方程，其形式为：

a2x2+a1x=b2y2+b1y

(4)

则其差分插补代码为：

jx1，jx2，jy1，jy2，F，G，jj，L

jx1：x的一阶差分；jx2：x的二阶差分；

jy1：y的一阶差分；jy2：y的二阶差分；

F：插补偏差；G：计数方向；

jj：曲线在x轴(或者y轴)上的投影长度；

L：加工用绝对坐标象限。

其中，jx1=a2+a1，jx2=2a2，jy1=b2+b1，jy2=2b2。在插补的过程中，必须保证jx1>0，jy1>0，其具体差分计算见相关参考文献[11]。F为插补偏差，F=Pn(x)-Qm(y)或者F=Qm(y)-Pn(x)，在插补初始化时，F=0。G为计数方向，用来判断投影方向。若曲线终点的切线斜率绝对值K大于1时，G=Gy，曲线的投影方向为y轴，否则G=Gx，曲线的投影方向为x轴。jj为曲线在计数方向上的计数长度。L为曲线加工起始段所在的加工用绝对坐标系象限号。在曲线的插补过程中，当二阶差分值为负值时，有可能出现一阶差分值为负值的情况。为使插补运算正常进行，必须改变坐标轴的进给方向，保证各一阶差分值为正，所以要调整L所在的加工用绝对坐标系的象限。正二次曲线差分插补的基本原理，如图3所示。

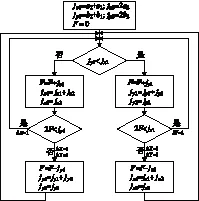
图3 正二次曲线差分插补基本原理图

3.2 差分插补原理在圆柱插补模式中的应用

3.2.1 由平面插补向圆柱插补的过渡

将上文中有关旋转轴与原直线轴的关系进行整理，并带入式(4)，得到：

(5)

由式(5)可知，经变换后的方程依然为正二次曲线方程，符合差分插补原理的基本要求。

由以上分析可知，基于差分插补原理的圆柱插补模式的各个参数与平面插补参数在形式上具有一致性。为了实现了平面插补与圆柱插补程序的统一，简化插补程序的编写，提高插补效率，并且易于编写数控程序，对于圆柱插补模式依然可以采用式(4)的插补代码形式。

在实际插补过程中，需要将输入的坐标等参数转换为以脉冲当量为单位的数值。在这一转换过程中，需要特别注意圆柱直径这一变量数值。由于旋转轴的角度脉动当量是固定不变的，而工件直径不同时，数控系统发出一次脉冲，转换到工件圆柱面上的直线距离也是不同的。即旋转轴的直线脉冲当量随着工件直径的不同而发生变化。

针对上述问题，本文引入圆柱插补模式缩放比例因子n，通过该比例因子来使插补程序适应由于工件直径的不同而导致旋转轴直线脉冲当量发生的变化，其表达式如下所示：

n=δ′/δ

(6)

其中：δ为原直线轴的直线脉冲当量，

δ′为旋转轴转换到圆柱型工件表面的直线脉冲当量。

3.2.2 圆柱插补模式的命令格式

通过以上分析，基于差分插补原理的圆柱插补模式可以直接采用平面内的差分插补方法。所以，在进入圆柱插补模式后，只需要编程人员提供圆柱工件的直径，其余参数按照圆柱展开后的平面计算即可。

圆柱插补模式的命令格式定义如下：

G11 参数① 参数②

其中：

参数①为旋转轴的代号，如A，B，C等。

参数②为圆柱工件的直径。当直径不为零时，开启圆柱插补模式；当直径为0时，取消圆柱插补模式。

4 基于差分插补原理的圆柱插补实验

通过参考有关差分插补的文献[11-15]，在VC++6.0的开发环境下，对基于差分插补原理的圆柱插补模式进行开发。在三坐标数控雕刻机设备上，采用上述插补模式，对圆柱表面进行圆与椭圆的雕刻实验。其实验结果，如图4所示。

图4 圆柱面雕刻实验

5 结论

通过研究差分插补原理在圆柱插补模式上的应用，拓展了基于差分插补原理数控系统的应用范围，为在经济性数控系统上实现圆柱表面的插补提供了重要的支持。在三坐标数控雕刻机上进行的实验，其结果表明基于差分插补原理的圆柱插补模式易于编程，能够实现二次曲线在圆柱表面的直接雕刻。为后期进一步研究回转体零件(如锥台等)表面复杂轮廓曲线的插补，打下了良好的基础。

[1] 黄友训.圆柱插补功能在数控车铣加工中心的应用[J]. 模具制造,2016,16(5):66-69.

[2] 杨应坡.圆柱插补在车削中心上的应用[J].机械工程师,2013(3):69-70.

[3] 韩式国,赵军,陈晓晓,等.数控编程技术及其典型应用研究[J].组合机床与自动化加工技术,2012(3):100-103.

[4] 黄伟斌.圆柱曲面上曲线的第四轴加工宏程序分析[J]. CAD/CAM与制造业信息化,2011(11):68-72.

[5] 陶辉.宏程序在柱面椭圆槽加工中的应用[J].煤矿机械,2013,34(7):125-126.

[6] 苟建峰,彭美武,卢万强,等.基于渐变非圆曲线轮廓零件的参数编程研究[J].组合机床与自动化加工技术, 2015(4):146-148.

[7] 曾峰,陶辉.浅谈圆柱插补指令(G07.1)在四轴加工中的应用[J].机床与液压,2011,39(2):146-147.

[8] 胡飞嘉.圆柱展开指令在铣削圆柱凸轮中的应用[J]. 金属加工(冷加工),2012(5):58-60.

[9] 袁名伟,袁国强.基于车铣加工中心圆柱插补功能的研究[J].机械工程师,2004(2):32-34.

[10] 王西建,冀勉.宏程序在非圆曲线轮廓车削加工中的应用[J].组合机床与自动化加工技术,2013(7):110-111,114.

[11] 王敏.差分插补方法及其在数控线切割机中的应用(一)[J].电加工,1981(4):16-22.

[12] 赵庆志.基于可重构理论的慢走丝线切割机床控制系统研究与设计[D].南京:南京航空航天大学,2005.

[13] 赵庆志,谭培红,高振华.抛物线ISO代码译成差分插补代码及其实现[J].机械设计与制造,2006(5): 57-59.

[14] 刘肖,赵庆志,于光伟,等.双曲线ISO代码译成差分插补代码及程序的实现[J].山东理工大学学报(自然科学版),2010,24(2):82-86.

[15] 王宜龙,赵庆志,王海涛.椭圆ISO代码译成差分插补代码及其程序的实现[J].机床与液压,2009,37(9): 54-55,118.

(编辑 李秀敏)

Research on Cylindrical Interpolation Model Based on Differential Interpolation

WANG Hong-jia， ZHAO Qing-zhi， YANG Zhao-bin

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255000, China)

In order to realize the direct interpolation of the conic of the cylindrical surface, the difference interpolation principle is applied to the cylindrical interpolation mode by analysing the cylindrical interpolation mode of turning-milling machines.The mathematical analysis of the cylindrical surface is carried out for obtaining the relationship between the cylindrical surface interpolation and the plane interpolation in order to realize the interpolation of conic on the cylinder surface.By introducing the cylindrical interpolation mode scaling factor, the unification of cylindrical interpolation and plane interpolation is realized, and the efficiency of NC programming and machining is improved.After the analysis of the conic difference interpolation code,the command format about cylindrical interpolation modes are defined.At the same time, the relevant verification experiments are taken.The experimental results show that the cylindrical interpolation mode based on the differential interpolation principle can achieve the direct interpolation of the conic of the cylindrical surface, and it is easy to understand and program.

differential interpolation；cylindrical interpolation model；axis of rotation；conic

1001-2265(2017)05-0014-03

10.13462/j.cnki.mmtamt.2017.05.004

2016-11-11；

2016-12-08

王宏甲(1988—)，男，山东潍坊人，山东理工大学硕士研究生，研究方向为数控技术与装备，计算机辅助设计与图形学，(E-mail)whj1988928@163.com；通讯作者：赵庆志(1962—)，男，山东日照人，山东理工大学教授，博士，研究方向为数控技术与装备、机电一体化技术，(E-mail)zhaoqzme@163.com。

TH162;TG659

A