重型数控机床伺服驱动中的惯量匹配分析*

张彦方，周 林，桑伟进，彭芳瑜，闫 蓉

(华中科技大学 国家数控系统工程技术研究中心，武汉 430074)

重型数控机床伺服驱动中的惯量匹配分析*

张彦方，周 林，桑伟进，彭芳瑜，闫 蓉

(华中科技大学 国家数控系统工程技术研究中心，武汉 430074)

在重型数控机床产业，伺服惯量匹配对进给伺服系统的动态性能有着非常重要的影响，文章搭建了数控机床进给伺服系统通用的全闭环仿真模型，以GMC1600H/2五坐标横梁移动龙门加工中心Y、Z轴为研究对象，分析了时域和频域下惯量比对单轴系统性能的影响以及Y、Z轴联动时不同惯量比对直线轨迹和圆形轨迹轮廓误差的影响，给出了直线加工和圆弧加工两种加工形式下较优的惯量比范围，并说明了在超过一定惯量比范围后，系统轮廓误差会呈现明显的波动，为数控机床伺服驱动中的惯量匹配提供了理论依据。

重型机床；伺服驱动；惯量匹配

0 引言

机械传动部件的转动惯量会影响整个系统的谐振频率以及动态性能，尤其对于重型机床其移动负载惯量大，所以必须处理好负载/电机的惯量匹配问题。根据牛顿第二定律有：系统加速转矩=系统转动惯量×角加速度 ，当进给系统电机选定之后，电机转矩最大值也就确定了，如果希望系统角加速度的变化小，应使系统转动惯量的变化小，则负载变化所占比例小些，这就是常说的“惯量匹配”[1]。

朱德志等人指出若仅考虑转矩匹配而忽略了惯量匹配，会影响交流伺服系统的灵敏度、伺服精度、瞬态响应时间等[1-2]。而且在双轴同步驱动伺服系统中，惯量不匹配会造成两轴运动不同步，系统出现振荡或抖动，降低加工精度，所以一定要处理好惯量匹配的问题。一般认为负载惯量越小，系统的动态响应越好；相反，负载惯量越大，电机越难控制，当负载惯量大于或等于3倍的电机转子惯量时，伺服电机的可控性会显著下降，系统可能出现工作不正常[3-5]，在高速切削下表现尤为突出。季晶晶[6]等提出，对于重型数控机床由于其自身的一些特点，各个部件惯量差异比较大，之间会存在响应不一致和参数不匹配的情况，导致其控制精度变差，其中惯性滞后是这类大惯量物体的一个明显特征，对精度影响尤其重要。吴沁[7]等针对大惯量的滚珠丝杠伺服进给结构，采用定量求解以及数值仿真的方式，对其中的非线性环节进行了研究，通过实验分析了大惯量进给系统动力学特性及系统参数的关系和匹配规律，总结出非线性情况下的一些加工策略。西安交大的刘辉[8]等人通过建立进给系统的双惯量模型，从能量耦合、闭环控制增益上限、闭环频率特性及抗干扰刚度等方面对负载惯量比进行了相应的仿真分析，并给出了综合考虑各项性能的进给系统负载惯量比设计步骤和方法。2012年，清华大学的Shao[9]等人通过对某并联机器人的研究，综合考虑机床共振频率、加速力矩、动态性能，结合仿真得出了惯量指标以及合适的惯量匹配范围，并得到推广应用。2015年，华中科技大学的杨森[10]通过建立机床虚拟样机的机电联合仿真平台，分析了不同驱动方式和不同加工工况下机床进给系统最佳负载惯量比。

为了使整个系统具有良好的匹配性能，提高工作效率，本文搭建了数控机床进给伺服系统通用的全闭环仿真控制模型，以GMC1600H/2五坐标横梁移动龙门加工中心Y、Z轴为研究对象，从时域和频域上分别仿真分析惯量比对系统的影响，并结合实际情况对双轴联动下系统轮廓误差进行仿真分析，最后给出了直线加工和圆弧加工两种加工形式下较优的惯量比，同时说明了在超过一定惯量比范围后，系统轮廓误差会呈现明显的波动。

1 伺服进给系统仿真模型

数控机床伺服控制单元与机械装置之间通过伺服电机输出扭矩联系起来，为了实现数控机床高精度的控制，现在机床一般采用全闭环控制方式，伺服系统对工作台的实际位置直接进行检测，并比较位置信息反馈值与指令位值，通过将差值放大实现对伺服电机速度和位置精准控制。于是在Simulink中建立数控机床进给伺服系统通用的全闭环仿真模型，如下面图1所示。

图1 进给系统全闭环仿真模型

2 惯量比对单轴系统性能影响分析

在机床实际的工作过程中由于工况的不同从而造成了不同惯量比下机床的动态响应特性的不同，合理的惯量匹配对伺服系统的动态响应特性有较大影响，它可以保证合理的响应速度，从而抑制谐振的发生，进一步改善重型机床低速爬行的现象，进而满足整机的最高运动速度、定位精度等技术性指标。为了使整个系统具有良好的匹配性能，提高工作效率，于是在Simulink中建立数控机床进给伺服系统通用的仿真模型，以GMC1600H/2五坐标横梁移动龙门加工中心Z轴为研究对象，进行仿真、分析惯量比对系统动态性能的影响。

2.1 惯量比对系统时域内特性的影响

2.1.1 惯量比对单位阶跃响应性能的影响

调节图1中的控制器参数，利用Simulink中PID调节器模块提供的tune功能可以实现控制器参数快速、简便调整，分别对速度环和位置环参数进行整定，使速度环超调量为20%，增大位置环比例增益使位置环不产生超调，然后对模型进行仿真分析，仿真模型包含五种惯量比，通过调整各自的位置环增益和速度环PI控制环节的参数，使其达到最优响应，仿真得到相应的瞬态响应指标参数如表1所示。

表1 不同惯量比的位置增益和指标参数

从表1中可以看出，随着惯量比的增加，系统的响应越慢，其到达峰值的时间逐渐增加，从0.114s增加到0.135s，而且达到稳定状态的时间也越长，从0.261s增加到0.311s。

2.1.2 系统控制增益上限与惯量比大小的关系

伺服控制增益将直接影响进给伺服系统的动态性能，如位置环控制增益将直接决定系统控制带宽和稳态时滞，进而影响进给伺服系统的响应快速性能、跟随误差以及轮廓误差，因此有必要对惯量比和系统增益上限之间的关系进行研究。以GMC1600H/2五坐标横梁移动龙门加工中心Z轴为例，仿真结果如表2所示。

表2 不同惯量比下的位置环增益上限

从表2中可以看出，随着惯量比增大，位置环增益上限逐渐减小，从14500减小到11700。这对于减小系统稳态跟随误差，提高机床加工精度有一定的帮助。若各轴位置环增益不匹配，会导致加工圆形时轨迹为椭圆，造成较大的加工误差。

2.1.3 系统跟随误差的大小与惯量比大小的关系

仿真分析在不同的惯量比下跟随误差的大小，以正弦信号作为输入信号，在上述五种惯量比的情况下仿真分析系统的跟随误差，结果如图2所示。

图2 不同惯量比下的跟随误差

由上图分析可以得到：随着负载惯量比的增大，系统的跟随误差随之增大。

2.1.4 系统抗干扰能力与惯量比大小的关系

在Simulink模型中，将输入设置为0，并施加2500N的干扰力，仿真得到不同惯量比下系统响应达到最大变形的时间，最大变形量和调整时间，如表3所示，并将这三个参数作为系统抗干扰能力的评价指标。

表3 不同惯量比下抗干扰能力

从表3中可以看出，随着惯量比的增加，系统的抗干扰能力逐渐增加，恢复到稳定状态的时间逐渐减小，从0.991s减小到0.665s。

2.2 惯量比对系统频域内特性的影响

2.2.1 惯量比对系统闭环频率特性的影响

根据图1可以得到该控制系统的闭环频率特性，记为：

分别求得下面五种惯量比下的幅频特性曲线，如图3所示，从图中可以看出随着负载惯量比的增大，系统控制带宽随着增加，振荡性减弱，但差别不是很明显。

图3 不同惯量比下幅频特性曲线

2.2.2 惯量比对系统抗干扰动刚度的影响

定义在不同频率干扰信号下产生单位偏差输出所需的干扰力大小为系统的抗扰动刚度，其表达式为：

通过计算整理得到五种不同惯量比下的系统抗干扰刚度，如图4所示。

图4 不同惯量比下系统抗扰动刚度

从图4中可以看出，不同惯量比系统在低频干扰下抗扰动刚度基本相同，且都随着频率增加系统抗扰动刚度有下降趋势；但在高频下随着惯量比增大，系统抗扰动刚度随之增加，且随着频率增大系统抗扰动刚度也随着增加，表现为高速切削下的抗扰动性能较强。因此当惯量比增大时，系统加工性能对切削力变化的敏感度减小，对各种不同的加工工况都能适应，机床受到扰动后的影响随之降低。

3 惯量比对双轴联动轮廓误差的影响分析

3.1 不同惯量比下直线轨迹轮廓误差仿真分析

在Simulink中搭建表示双轴联动直线运动轨迹轮廓误差的计算模型，如图5所示。

图5 直线运动轨迹轮廓误差计算模型

为了对比分析惯量比对直线运动轨迹轮廓误差的影响，通过修改龙门加工中心Y、Z轴仿真模型中负载质量从而改变惯量比，在改变一个轴的负载质量时保证另一个轴负载质量不变。为了使仿真结果影响因素尽量少，各种惯量比下仍采用原控制器参数。仿真中输入信号进给速度F为2000mm/min，轨迹直线与Y轴正向夹角θ为45°。

改变Y轴负载质量，得到五组惯量比下的轮廓误差随时间变化曲线及其局部放大图，如6所示，可以看出在刚启动时系统轮廓误差存在一定波动，最后逐渐稳定为一个定值。

(a)整体图

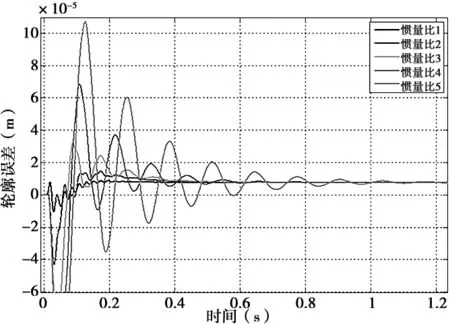
(b)局部放大图图6 直线轨迹轮廓误差(Y轴负载惯量改变)

同样改变Z轴负载质量，得到五组惯量比下的轮廓误差随时间变化曲线及其局部放大图，如图7所示。

(b)局部放大图图7 直线轨迹轮廓误差(Z轴负载惯量改变)

从两组仿真结果可以看出，随着惯量比增加系统启动加速阶段轮廓误差波动随之增大，反映到加工轮廓上，表现为启动阶段加工出的轮廓非标准直线，会出现一定抖动。Y轴惯量比改变引起的轮廓误差波动较Z轴小，但惯量比在1～3之间变化时，两种情况下启动加速阶段的轮廓误差波动都在可接受范围内。对于直线加工，为了获得较好的轮廓精度，惯量比在1～3是较优的选择。

3.2 不同惯量比下圆形轨迹轮廓误差仿真分析

在Simulink中搭建表示双轴联动圆形运动轨迹轮廓误差的计算模型，如图8所示，其中斜坡信号表示夹角θ随时间的变化，其大小为上述正弦输入信号的角频率。

图8 圆形运动轨迹轮廓误差计算模型

在Simulink中设置仿真输入信号：半径R为30mm，进给速度F为2000mm/min，改变Y、Z轴负载惯量，仍采用原控制器参数，仿真得到五组惯量比下圆形运动轨迹轮廓误差随时间变化曲线，如图9、图10所示。

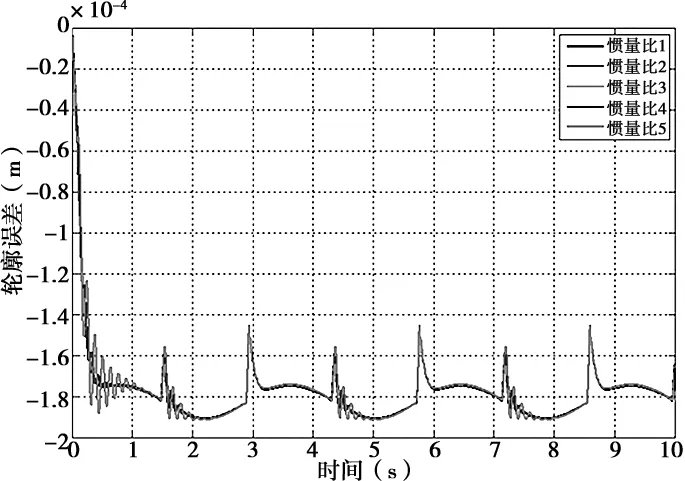
(a)整体图

(b)局部放大图图9 圆形轨迹轮廓误差(Y轴负载惯量改变)

(a)整体图

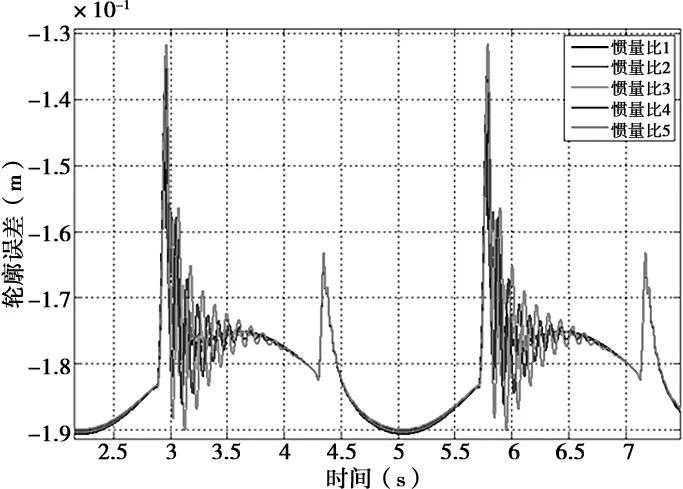
(b)局部放大图图10 圆形轨迹轮廓误差(Z轴负载惯量改变)

从图9、图10中可以看出，在加工圆形轨迹时，轮廓误差呈现周期性变化，随着惯量比增加，轮廓误差在各轴换向时波动越来越大，表现为象限位置处产生“尖峰”，为保证加工圆弧质量，应尽量减小这种波动。Y轴惯量比在1～4之间变化时，其轮廓误差变化不明显，在惯量比为5时出现明显波动；Z轴惯量比改变对轮廓误差影响较大，惯量比在3～5之间时波动十分明显。

4 总结

本文在Simulink中建立数控机床进给伺服系统通用的仿真模型，仿真得到随着惯量比增加系统在时域、频域内的特性以及双轴联动下直线轨迹和圆形轨迹轮廓误差的变化：(1)单轴系统在时域内的特性：随着惯量比的增加，系统的响应越慢，到达峰值时间逐渐增加，系统的跟随误差逐渐增大，达到稳定状态的时间也越长，位置环增益上限逐渐减小，恢复到稳定状态的时间逐渐减小，抗干扰能力逐渐增加。

(2)单轴系统在频域内的特性：随着惯量比的增加，系统的控制带宽逐渐增加，震荡性逐渐减弱；不同惯量比系统在低频干扰下抗扰动刚度基本相同，且都随着频率增加有下降趋势；但在高频下随着惯量比增大，系统抗扰动刚度随之增加，且随着频率增大系统抗扰动刚度也随着增加，表现为高速切削下的抗扰动性能较强。

(3)双轴联动轮廓误差的变化：随着惯量比的增加，系统在启动加速阶段的直线轮廓误差波动随之增大，在换向时圆轮廓误差波动随之增大，并且得到两种加工形式下较优的惯量比:对于直线加工，为了获得较好的轮廓精度，惯量比在1～3是最优的选择；对于圆弧加工，惯量比在1～4是最优的选择。

[1] 朱德志,刘洪亮. 惯量匹配在改善数控龙门镗铣床性能中的作用[J]. 制造技术与机床,2007(2):61-63.

[2] 余清华,朱宏杰,郭军,等. 数控机床进给系统必须惯量匹配[J]. 金属加工(冷加工),2011(3):53-54.

[3] 王勇. 惯性匹配在伺服电动机选型中的应用[J]. 金属加工(冷加工),2011(15):72-73.

[4] 张政泼. 数控机床进给传动系统的惯量分析和校核[J]. 装备制造技术,2010(10):37-41.

[5] 李幼涵. 机器设计中伺服电机及驱动器的选型[M]. 北京:机械工业出版社,2012.

[6] Guo J, Ji J,Yang F, et al. Adaptive robust control for servo system with friction and input dead-zone nonlinearity[C]//Modelling, Identification & Control (ICMIC), 2012 Proceedings of International Conference on.IEEE, 2012: 993-997.

[7] Wu Q,Yang J,Rui Z, et al. Optimization and Distributing Research of Measuring Points for Thermal Error of CNC Machine Based on Weighted Grey Relative Analysis[M].Intelligent Computing and Information Science. Springer Berlin Heidelberg, 2011.

[8] 刘辉,黄莹,赵万华,等. 多因素耦合条件下数控机床进给系统负载惯量比的综合分析与设计[J]. 机械工程学报, 2014, 50(9):108-113.

[9] Shao Z F, Tang X, Chen X, et al. Research On The Inertia Matching Of The Stewart Parallel Manipulator[J]. 2012, 28(6):649-659.

[10] 杨森. 重型机床惯量匹配研究与电机选型软件开发[D]. 武汉:华中科技大学,2015.

(编辑 李秀敏)

Analysis of Inertia Matching in Servo Drive of NC Machine Tools

ZHANG Yan-fang， ZHOU Lin, SANG Wei-jin， PENG Fang-yu， YAN Rong

(National Numerical Control System Engineering Research Center, Huazhong University of Science and Technology,Wuhan 430074,China)

In heavy machine tool industry. Servo inertia matching has a very important influence on the dynamic performance of servo system of heavy machine tool. In this paper. a general closed loop simulation model of the feed servo system of CNC machine tool was built. To GMC1600H/2 five coordinate beam mobile gantry machining centerY、Zaxisastheresearchobject.Undertheeffectiveofthesimulationmodel.theeffectofinertiaratioontheperformanceofthesingleaxissystemwasanalyzedinthetimedomainandfrequencydomain.AndthevariationofthecontourerrorofthelinearandcirculartrajectorieswithdifferentinertiaratiowassimulatedandanalyzedinSimulink.Attheendofthepaper.thepreferableinertiaratioofthetwomachiningformsofstraightlineandcirculararcweregiven.Atthesametime.itshowedthatthecontourerrorofthesystemwouldappearobviouslyfluctuationwhentherangeofinertiaratiowasbeyondacertainrange.ThetheoreticalbasiswasprovidedfortheinertiamatchingintheservodriveoftheNCmachinetools.

heavy machine tool;servo drive; inertia matching

1001-2265(2017)05-0005-04

10.13462/j.cnki.mmtamt.2017.05.002

2016-07-21；

2016-08-27

“高档数控机床与基础制造装备”国家科技重大专项(2013ZX04013-011)

张彦方(1989—)，女，河南漯河人，华中科技大学硕士研究生，研究方向为机电联合仿真， (E-mail)zyf826525@126.com。

TH166;TG659

A