全光纤电流互感器灵敏度特性研究

肖智宏 ，程 嵩 ，张国庆 ，郭志忠 ，闫培丽 ，于文斌

（1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001；2.国网北京经济技术研究院，北京 100052；3.哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150001）

0 引言

随着智能电网的发展，传输线路的电压等级不断提高，传统的电磁式电流互感器已经不能满足要求［1-5］，发展新型电流互感器迫在眉睫。全光纤电流互感器［6-9］FOCT（Fiber Optic Current Transformer）是基于Sagnac干涉法的一种新型电流互感器，其将光作为一种载体，将被测电流的信息通过传感光纤感应到光信号中，再通过信号处理解调出来，这种方法克服了传统电磁式互感器的种种弊端，具有动态范围宽、绝缘性能好、测量精度高等优点［10-14］。

虽然FOCT具有上述优点，但是其小电流测量精度较差。这主要是由于传感光纤的Verdet常数较小，所以FOCT灵敏度较低，传感信号低于检测系统分辨的下限。为了增强FOCT对小电流分辨的能力，通常做法是提高信号处理系统分辨小信号的能力和提高FOCT的灵敏度。文献［15］提出了传感光纤匝数和数字量输出位数是影响FOCT小电流测量精度的原因，并通过改进信号处理电路和增多光纤匝数来提高小电流测量精度，但是未对传感环匝数对FOCT灵敏度特性的影响进行深入研究。文献［16］指出了传感环匝数越多，FOCT测量精度越高，但可能会使法拉第偏转角超过2π，从而降低动态范围，然而实际应用中发现，随着传感环匝数的增多，往往法拉第偏转角尚未达到2π时，FOCT的测量精度就开始下降。目前通过改进信号处理方式和算法来提高FOCT测量小电流的精度已有广泛研究，但尚无针对FOCT灵敏度特性的研究。

本文建立了FOCT灵敏度特性数学模型，该模型揭示了单位长度线性双折射、传感环半径和光纤缠绕匝数是影响FOCT灵敏度的3个重要因素。通过该模型进一步推导，表明FOCT传感光纤最优长度只与单位长度线性双折射有关，而与传感环半径和光纤缠绕匝数无关。通过仿真分析单位长度线性双折射、传感环半径和光纤缠绕匝数对FOCT灵敏度的影响，可知传感光纤在最优长度情况下，光纤缠绕最优匝数与传感环半径和线性双折射密切相关，且超过最优匝数时FOCT灵敏度下降，而线性双折射越低、传感环半径越小，则FOCT灵敏度越高，测量小电流精度越高。最后通过实验验证了仿真分析和所提结论的正确性，对工程实践具有重要指导意义。

1 FOCT原理

FOCT［17-20］是一种对称互易结构的光纤互感器，其结构原理如图1所示。FOCT能够有效地降低环境温度、振动等外界影响，提高测量系统的稳定性和测量结果的准确度。

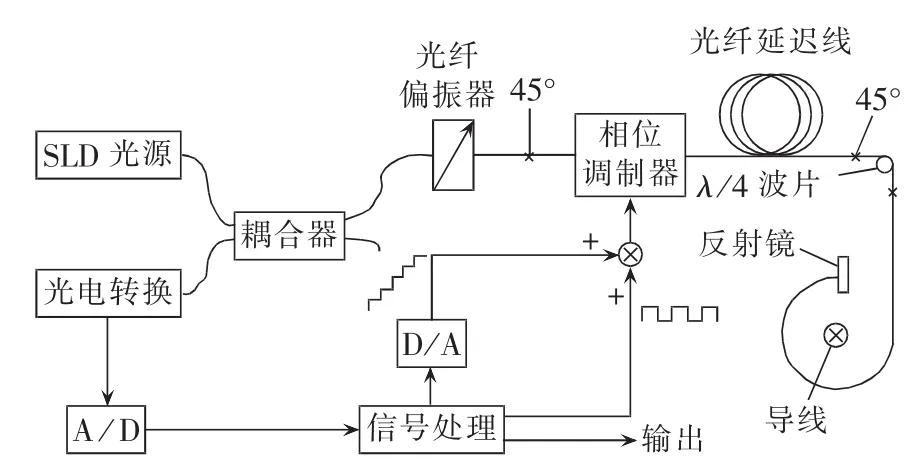
图1 反射式Sagnac FOCT原理图Fig.1 Schematic diagram of in-line Sagnac FOCT

由SLD光源发出的光经过耦合器后，通过光纤偏振器起偏，形成线偏振光。线偏振光再以45°平均注入保偏光纤的x轴和y轴传输。线偏振光通过保偏光纤传输到相位调制器进行初始相位调制后，再传输到λ/4波片。当这2束正交模式的线偏振光通过λ/4波片后，x轴和y轴的线偏振光就分别转变为左旋和右旋的圆偏振光，进入传感光纤。由于传输电流产生磁场的法拉第效应，这2束圆偏振光以不同的速度传输，产生相位差。2束圆偏振光由反射镜反射后，它们的偏振模式互换（即左旋光变为右旋光，右旋光变为左旋光）并第2次穿过传感光纤，同时和电流产生的磁场再次发生相互作用，使产生的相位差加倍。然后λ/4波片再把含有法拉第效应的2束圆偏振光转变回模式互换了的正交线偏光（原来的x轴线偏振光转换到y轴，y轴线偏振光转换到x轴）。通过相位调制器进行二次相位调制后，传输到偏振器使2束模式正交的线偏振光干涉。最后干涉光传输到光电转换器进行信号采集，并转换为电信号进行处理。

理想 FOCT 的信号输出为［21］：

其中，φf为法拉第旋转角；N为传感光纤缠绕的匝数；V为Verdet常数；I为被测导线电流值。

由式（1）可以看出，在理想情况下，传感光纤缠绕的匝数N越多，FOCT的灵敏度越高，检测小电流的能力越强。然而在实际应用中，由于传感光纤中存在线性双折射，传感光纤缠绕的匝数N超过一定值后，FOCT的灵敏度会随着缠绕匝数的增多而下降。

2 FOCT灵敏度特性模型

由于传感光纤主要采用单模光纤，而单模光纤中存在固有线性双折射和由于温度、外力等外部原因引起的双折射。固有线性双折射主要是由于光线中残余内应力或者纤芯不圆等原因引起的，不会随着外界的影响而改变。而温度变化导致的线性双折射实质上也是应力双折射的一种，会随着外界温度的波动而改变［22］。因此传感光纤中线性双折射引起的总相位差为：

其中，δ为传感光纤中所有线性双折射导致的总相位差；δc为固有线性双折射导致的相位差；δs为温度变化导致的线性双折射相位差。

考虑光纤中线性双折射作用的影响远大于磁光效应，即有 δ≫φf时，式（1）变换为：

目前传感光纤缠绕多采用石英骨架螺旋缠绕和柔性缠绕等技术，有效降低了内应力，且不易随温度变化或时间推移而改变，具有较好的一致性。因此传感光纤中线性双折射可表示为：

其中，L为传感光纤总长度，L=2πrN；δ0为单位长度传感光纤含有的线性双折射。将式（4）代入式（3）可得：

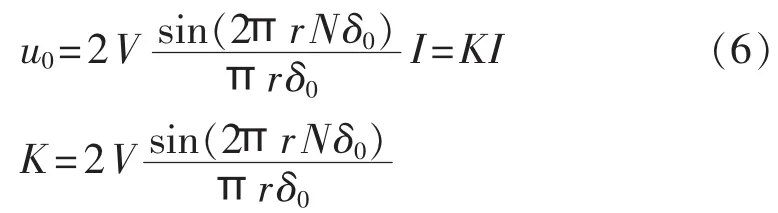
其中，K为FOCT灵敏度。

由式（5）可以看出，当采用同一种型号的传感光纤绕制成半径相同的传感环时，为了提高FOCT的灵敏度，则有：

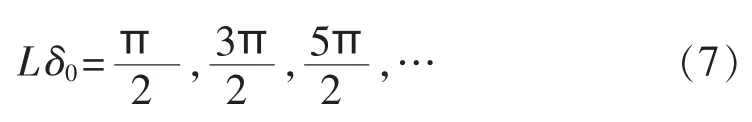
定义最优长度L0为采用最短传感光纤绕制成半径相同的传感环而使FOCT的灵敏度最高，则有：

由式（8）可以看出，传感光纤的最优长度只与δ0有关。对于δ0相同的传感光纤，即使缠绕成半径不同的传感环，其最优长度L0也相同。结合式（5）可以看出，当传感光纤长度为最优长度时，传感环半径r越小，FOCT的灵敏度越高，测量小电流精度越高。

定义最优缠绕匝数N0为采用长度为L0的传感光纤绕制成半径为r的传感环所缠绕的匝数，由L=2πrN 和式（8）得：

由式（9）可以看出最优匝数N0与δ0和r成反比，δ0和r越小，则最优匝数N0越大。

需要指出，这里所定义的N0为整数。由于式（9）的计算结果不一定为整数，因此需要四舍五入取整。

通常为了使检测系统能够准确分辨小电流的传感信号，应使：

其中，umin为检测系统能分辨的最小传感信号值。

结合式（6）推导出FOCT能准确分辨传感电流的下限为：

其中，Imin为FOCT能够准确测量的最小电流值。

由式（11）可以看出，FOCT灵敏度K越高，则Imin越小，FOCT的小电流测量能力越强。

3 仿真与分析

3.1 线性双折射对灵敏度的影响

将δ0不同的传感光纤都缠绕成匝数为28匝、半径为0.1 m的传感环。此时传感光纤长度都相同且为非最优长度，则由式（6）得到传感光纤长度相同的情况下，不同的δ0对FOCT灵敏度的影响曲线如图2所示。

图2 线性双折射对FOCT灵敏度影响的仿真曲线Fig.2 Simulative curves of FOCT sensitivity vs.linear-birefringence

同时针对δ0不同的传感光纤，根据式（8）分别取其对应的最优长度L0，并缠绕成半径为0.1m的传感环。由式（6）得到传感光纤为最优长度的情况下，不同的δ0对FOCT灵敏度的影响曲线如图2所示。

由图2可以看出，当传感光纤长度为非最优长度时，随着δ0的增大，FOCT灵敏度振荡衰减。结合式（8）可以得出，随着δ0的增大，其对应的最优长度L0减小，FOCT灵敏度也相应下降。当δ0相同且传感光纤长度为最优长度时，FOCT灵敏度最高。

3.2 光纤缠绕匝数对灵敏度的影响

通常FOCT采用低线性双折射光纤作为传感材料，因此分别取 δ0为 0.09 rad/m 和 0.04 rad/m、r为0.1m。 由式（8）可知，δ0=0.09 rad/m 时，最优匝数 N0=28；δ0=0.04 rad/m 时，最优匝数 N0=62。结合式（6）可以得到光纤缠绕匝数对FOCT灵敏度的影响曲线如图3所示。

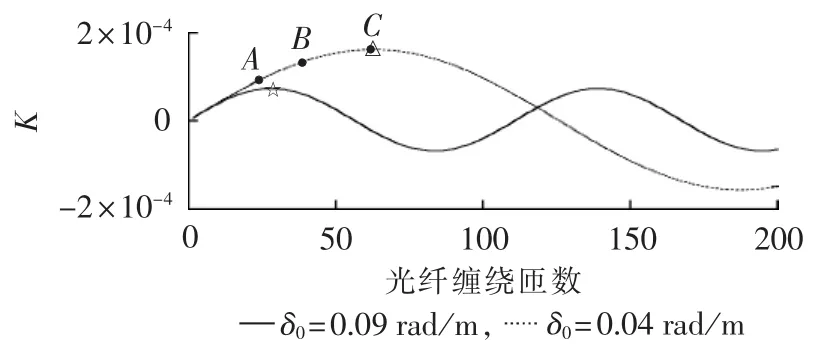
图3 光纤缠绕匝数对FOCT灵敏度影响的仿真曲线Fig.3 Simulative curves of FOCT sensitivity vs.fiber turns

图3中，“☆”对应N0=28时的FOCT灵敏度，点C为N0=62时的FOCT灵敏度。由图3可以看出，当光纤缠绕匝数低于最优匝数N0时，随着光纤缠绕匝数的增多，在一定范围内FOCT灵敏度与匝数近似成正比，即FOCT灵敏度随光纤缠绕匝数的增多而增高；当光纤缠绕匝数为最优匝数N0时，FOCT灵敏度最高，且δ0越小、N0越大，其线性增长段区域越宽；当光纤缠绕匝数超过最优匝数N0时，FOCT灵敏度反而下降，分辨小电流能力降低。

图3中点A对应能够准确分辨互感器标准要求最小电流值所需缠绕的最低匝数，即当缠绕匝数低于该值时，FOCT不能够分辨出标准要求的最小电流值，则由式（6）和式（11）可知：

通常FOCT采用线性双折射值很低的传感光纤，因此最优匝数N0可能会远大于Nmin。过多的光纤缠绕匝数虽然能够大幅提高灵敏度，但是随着缠绕匝数的增多，其灵敏度增长率减小，传感光纤利用率反而降低了，灵敏度曲线进入饱和区域。同时考虑FOCT灵敏度和光纤利用率，因此选取有效匝数Ne作为光纤缠绕匝数较为合理。

定义有效匝数Ne为灵敏度增长效率与灵敏度乘积最高的匝数，即图3中点B对应的匝数，则有：

其中，K′为灵敏度的导数，表征灵敏度的增长率。

由算例可知，δ0=0.04 rad/m的传感光纤，其最优匝数N0＝62，其有效匝数Ne=31。

3.3 传感环半径对灵敏度的影响

针对半径不同的传感环，都取光纤缠绕匝数为28、δ0为0.05 rad/m，此时传感光纤长度依据不同传感环半径而变化且为非最优长度，则由式（6）可得到传感环半径对FOCT灵敏度的影响曲线如图4所示。

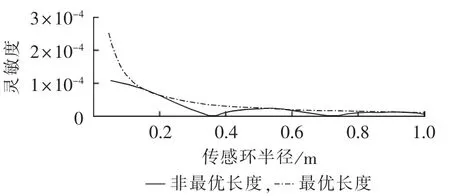
图4 传感环半径对FOCT灵敏度影响仿真曲线Fig.4 Simulative curves of FOCT sensitivity vs.coil radius

同样取 δ0为 0.05 rad/m，根据式（8）取其对应最优长度为31.42 m，缠绕成半径不同的传感环，则由式（6）得到传感环半径对FOCT灵敏度的影响曲线如图4所示。

由图4可以看出，当传感光纤长度为非最优长度时，随着传感环半径的增大，FOCT灵敏度振荡衰减，对小电流的分辨能力下降。结合式（9）可以得出，随着传感环半径增大，其对应的最优匝数N0减小，FOCT灵敏度也相应下降。当传感环半径相同且传感光纤长度为最优长度L0时，FOCT灵敏度最高。

4 实验

将同一型号的长17.6 m、δ0为 0.05 rad/m 的传感光纤分别绕制成传感环半径为0.09 m、匝数为30匝的A型FOCT，传感环半径为0.1 m、匝数为28匝的B型FOCT，传感环半径为0.11 m、匝数为26匝的C型FOCT以及传感环半径为0.12 m、匝数为24匝的D型FOCT。分别对A型、B型、C型和D型FOCT施加600 A额定电流，测得：A型FOCT的灵敏度为6.1×10-3，比差为0.020%；B型 FOCT的灵敏度为5.7×10-3，比差为0.016%；C型 FOCT的灵敏度为5.3×10-3，比差为0.022%；D型FOCT的灵敏度为5.0×10-3，比差为0.008%。然后分别施加1%、2%、3%、4%、5%、20%、40%、60%、80%、100%、120%的额定电流，测得A型、B型、C型和D型FOCT的比差曲线如图5所示，图中p为施加电流与额定电流的百分比。

图5 传感环半径对FOCT准确度的影响Fig.5 Influence of coil radius on accuracy of FOCT

由图5可以看出，当测量5%～120%的额定电流时，A型、B型、C型和D型FOCT的精度相似，说明灵敏度差异在测量较大电流时影响不大；当测量1%～4%的额定电流时，A型、B型、C型和 D型FOCT的精度逐渐降低，说明灵敏度差异对小电流测量精度有很大的影响。由相同长度的传感光纤缠绕的传感环半径越小，FOCT的灵敏度越高，比差越小，测量小电流的精度越高。

5 结论

本文建立了FOCT灵敏度特性数学模型，该模型揭示了单位长度线性双折射、传感环半径和光纤缠绕匝数是影响FOCT灵敏度的3个重要因素，通过该模型仿真和实验得到以下结论。

a.传感光纤的最优长度只与单位长度线性双折射有关，而与传感环半径和光纤缠绕匝数无关。即当用同型号传感光纤绕制成不同半径的传感环时，其传感光纤最优长度是相同的，且传感光纤为最优长度时，FOCT灵敏度也最高。

b.光纤缠绕匝数越多，FOCT灵敏度不一定越高，FOCT灵敏度随着缠绕匝数增多呈正弦振荡。当光纤缠绕匝数低于最优匝数时，灵敏度随着匝数增多而增大；当光纤缠绕匝数为最优匝数时，FOCT灵敏度最高；当光纤缠绕匝数多于最优匝数时，随着缠绕匝数的增多，FOCT灵敏度反而下降。

c.采用有效匝数不但能够满足FOCT灵敏度的要求，还能够有效地兼顾经济性和利用率，是较为合理的选择。

d.采用最优长度传感光纤绕制成不同半径的传感环，FOCT灵敏度随传感环半径的增大而降低，相应测量小电流的精度也降低。同样采用不同单位长度线性双折射光纤，FOCT灵敏度随着单位长度线性双折射的增大而降低。

［1］陈安伟，乐全明，冯亚东，等.全光纤电流互感器温度性能优化方法［J］.电力自动化设备，2011，31（1）：142-145.CHEN Anwei，LE Quanming，FENG Yadong，et al.Temperature performance optimization of FOCT［J］.Electric Power Automation Equipment，2011，31（1）：142-145.

［2］于文斌，张国庆，路忠峰，等.光学电流互感器的抗干扰分析［J］.电力系统保护与控制，2012，40（12）：8-18.YU Wenbin，ZHANG Guoqing，LU Zhongfeng，et al.Analysis of resistance disturbance capability of optical current transformers［J］.Power System Protection and Control，2012，40（12）：8-18.

［3］王佳颖，郭志忠，张国庆，等.光学电流互感器长期运行稳定性的试验研究［J］.电网技术，2012，36（6）：37-41.WANG Jiaying，GUO Zhizhong，ZHANG Guoqing，et al.Experimental investigation on optical current transducer’s long-term operation stability［J］.Power System Technology，2012，36（6）：37-41.

［4］CEASE T W，JOHNSTON P.A magneto-optic current transducer［J］.IEEE Transactions on Power Delivery，1990，5（2）：548-555.

［5］王玥坤，王政平，孙帅.法拉第旋光器温度特性对无源解调全光纤电流互感器的影响［J］.电网技术，2013，37（1）：206-210.WANG Yuekun，WANG Zhengping，SUN Shuai.Effect of temperature characteristic of faraday rotator on passively demodulated all-opticalfiber currenttransformers ［J］.Power System Technology，2013，37（1）：206-210.

［6］LEE B.Review of the present status of optical fiber sensors［J］.Optical Fiber Technology，2003，9（2）：57-79.

［7］刘杰，赵洪，王鹏，等.可温度自动跟踪的高精度光纤光栅电流互感器［J］.中国电机工程学报，2012，32（24）：141-147.LIU Jie，ZHAO Hong，WANG Peng，et al.High accuracy current transformers with an automatic temperature tracking system based on FBG［J］.Proceedings of the CSEE，2012，32（24）：141-147.

［8］SMITH A M.Optical fibers for current measurement applications［J］.Optics and Laser Technology，1980，12（1）：25-29.

［9］李建中，李泽仁，张登洪，等.全光纤电流互感器λ/4波片制作工艺［J］.红外与激光，2013，42（8）：2167-2172.LI Jianzhong，LI Zeren，ZHANG Denghong，et al.Fabrication of λ/4 wave plate for fiber optic current transducer［J］.Infrared and Laser Engineering，2013，42（8）：2167-2172.

［10］王立辉，何周，刘锡祥，等.反射式光纤电流互感器光波偏振态相互转换过程中的误差特性［J］.电工技术学报，2013，28（1）：173-174.WANG Lihui，HE Zhou，LIU Xixiang，et al.Error characteristics in mutual conversion process of reflective fiber optic current transducer’s optical polarization state［J］.Transactions of ChinaElectrotechnical Society，2013，28（1）：173-174.

［11］陈硕，刘占元，刘鹏飞，等.基于光纤反射腔的高灵敏电流传感器方案［J］.光学与光电技术，2014，12（1）：19-23.CHEN Shuo，LIU Zhanyuan，LIU Pengfei，et al.A scenario of high sensitivity current sensor based on optical fiber reflection cavity［J］.Optics & Optoelectronic Technology，2014，12（1）：19-23.

［12］王巍，吴维宁，王学锋.调制器调制系数对光纤电流互感器测量精度的影响［J］.电力系统自动化，2012，36（24）：64-68.WANG Wei，WU Weining，WANG Xuefeng.Effect of modulator modulation coefficient on measuring accuracy of fiber optic current sensor［J］.Automation of Electric Power Systems，2012，36（24）：64-68.

［13］刘彬，叶国雄，郭克勤，等.基于Rogowski线圈的电子式电流互感器复合误差计算方法［J］.高电压技术，2011，37（10）：2391-2397.LIU Bin，YE Guoxiong，GUO Keqin，et al.Calculation method of composite error for electronic current transformers based on Rogowski coil［J］.High Voltage Engineering，2011，37（10）：2391-2397.

［14］穆杰，王嘉，赵卫，等.消除振动敏感性与温度漂移的光纤电流互感器［J］.高电压技术，2010，36（4）：980-986.MU Jie，WANG Jia，ZHAO Wei，et al.Vibration and temperature insensitive fiber-optic current transducer［J］.High Voltage Engineering，2010，36（4）：980-986.

［15］张朝阳，雷林绪，王成昊.数字闭环光纤电流互感器小电流测量准确度分析［J］.仪表技术与传感器，2012（10）：7-10，19.ZHANG Chaoyang，LEI Linxu，WANG Chenghao.Low current measurement error analysis of digital closed-loop fiber optic current transformer［J］.Instrument Technique and Sensor，2012（10）：7-10，19.

［16］许扬，陆于平，卜强生，等.光纤电流互感器对保护精度和可靠性的影响分析［J］.电力系统自动化，2013，37（16）：119-124.XU Yang，LU Yuping，BU Qiangsheng，et al.Analysis for effect of fiber-optic current transformer on protection accuracy and reliability［J］.Automation of Electric Power Systems，2013，37（16）：119-124.

［17］李传生，张春熹，王夏霄，等.Sagnac型光纤电流互感器变比温度误差分析与补偿［J］.电力自动化设备，2012，32（11）：102-106.LI Chuansheng，ZHANG Chunxi，WANG Xiaxiao，et al.Analysis and compensation of ratio temperature error for Sagnac fiberoptic current transformer［J］.Electric Power Automation Equipment，2012，32（11）：102-106.

［18］曹辉，杨一凤，刘尚波，等.用于光纤电流传感器SLD光源的温度控制系统［J］.红外与激光工程，2014，43（3）：920-926.CAO Hui，YANG Yifeng，LIU Shangbo，et al.Temperature control system for SLD optical source of FOCT ［J］.Infrared and Laser Engineering，2014，43（3）：920-926.

［19］BLAKE J，TANTASWADIP，DE CARVALHO R T.In-line Sagnac interferometer current sensor［J］.IEEE Transactions on Power Delivery，1996，11（1）：116-121.

［20］FROSIO G.Reciprocal reflection interferometer for a fiber-optic Faraday current sensor［J］.Applied Optics，1994，33（25）：6111-6122.

［21］廖延彪.光纤光学［M］.北京：清华大学出版社，2000：74-77.

［22］程嵩，郭志忠，张国庆，等.全光纤电流互感器的温度特性［J］.高电压技术，2015，41（11）：3843-3848.CHENG Song，GUO Zhizhong，ZHANG Guoqing，et al.Temperature characteristic of fiber optic current sensor［J］.High Voltage Engineering，2015，41（11）：3843-3848.