主动扰动技术在停电配电线路相间故障检测中的应用

朱 珂，李德强，妥建军，张 波

（山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061）

0 引言

我国配电网广泛采用中性点非有效接地运行方式。当线路因相间短路或其他原因停电后，如果盲目进行重合闸或尝试性送电，则有可能因故障点的存在而产生冲击，进而对断路器及上游变压器等设备造成不利影响，恶化电能质量。尤其是随着电缆的广泛应用，配电线路重合闸的成功率日益降低，导致许多地市级电力公司规定只要含有电缆的配电线路其自动重合闸都要全部退出，从而明显降低了配电网的供电可靠性［1-2］。因此，研究断路器合闸送电前配电线路相间是否存在故障对于提高供电可靠性和改善电能质量具有实际意义。

当前对停电线路是否存在故障的判别方法主要有无源法和有源法2种。无源法基于线路跳闸后残留电磁能释放过程中体现出来的某些电气量的特性对线路是否还带有故障进行判定［3-10］。这类方法主要用于输电线路的自适应重合闸，但不适用于因跳闸而立刻彻底失电的单电源供电配电线路。有源法向停电线路注入一个具有一定特征的激励信号，通过系统对此激励信号的响应来判定发生在线路上的故障类型。文献［11-12］利用2个变压器中间串联一个电力电子开关构成的支路与高压断路器并联，在对长时间停电线路送电之前，控制电力电子开关将系统上游电源瞬时施加在停电配电线路上，通过分析系统响应对线路是否还存在故障进行判定。该方法思路新颖，但现场可实施性差，且无法避免对上游系统造成的冲击，从而限制了其在实际中的应用。文献［13］利用特殊的高压断路器直接将上游系统电源短时加到经较长时间停电的配电线路上，通过检测分析所产生的电流幅值以判断线路是否存在故障。这种方法不仅需要更换高压断路器，且仍会对上游系统产生明显冲击。文献［14］提出利用高压电容对故障线路高频振荡放电所产生的行波来识别故障类型。配电网分支众多，行波折反射严重，会给故障性质的判定带来困难。

本文针对当前国内配电网因合闸于带故障线路而可能导致的不利影响，提出一种配电线路停电状态下的自动相间故障检测技术。该技术无需通信，可避免配电线路盲目性合闸，既可用于配电线路自适应重合闸，也可用于线路停电一段时间后的尝试性送电，理论、仿真分析和模拟实验都验证了该方法的有效性。

1 相间故障检测方案

1.1 工作原理

在配电变压器低压侧经电力电子开关单元（图1中用晶闸管表示）接入一逆变交流电源。当中压配电线路三相跳闸且故障点断电去游离后，晶闸管单元受控导通，将经配电变压器升压的逆变电源电压短时施加在停电线路故障相间，通过对断路器下游暂态电压的检测与分析来判定故障性质，进而决定断路器的投入与否，具体方案实施原理如图1所示。

通过控制晶闸管的触发角可灵活控制施加在停电线路故障相间暂态电压的幅值，从而保证击穿各种隐性故障点。图2为阻感性负载时以不同触发角控制晶闸管导通产生的暂态电压、电流波形图。

图1 方案实施原理图Fig.1 Schematic diagram of implementation

图2 阻感性负载时不同触发角下产生的暂态电压、电流简化波形示意图Fig.2 Transient voltage and current waveforms for resistor-inductor load and different firing angles

1.2 故障检测判据的建立

基于图1所示的方案实施原理的简化等效电路如图3所示。其中Z1=R1+jωL1为逆变电源所在低压侧负荷等效阻抗，Z2=R2+jωL2为高压侧负荷等效阻抗，LT为变压器漏电感，RF为故障电阻，开关K断开代表无故障，闭合代表故障存在。

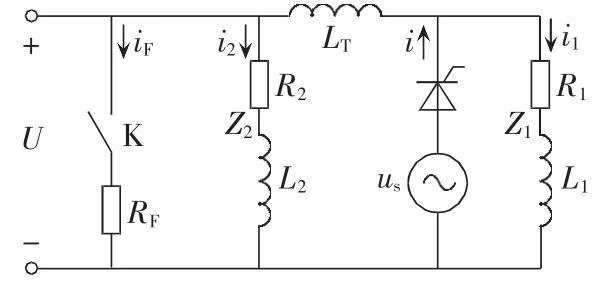
图3 方案简化等效电路图Fig.3 Simplified equivalent circuit

（1）开关断开，无故障情况。

在晶闸管两端电压过零前，施加触发脉冲使其导通，在电流过零时，晶闸管自动关断。由于晶闸管关断使得电流i1与i2之和强制为0，因此关断瞬间端口电压U将会产生突变。

设晶闸管的触发角为φu，则逆变电源的电压表达式为：

基于电路理论，可以求出流过Z2的电流为：

其中，为负载阻抗角T为晶闸管的导通时间；晶闸管的导通角为δ=ωT。晶闸管导通截止前一瞬间Z2两端的电压（即端口电压）为：

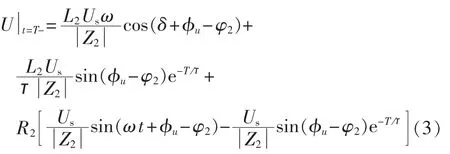
由于电感L2上的电流i2不能突变，所以有：

将作为初始条件，可以求出晶闸管导通截止后流过Z2的电流为：

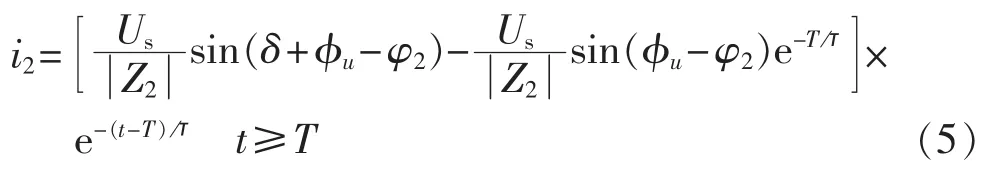
晶闸管导通截止后一瞬间，Z2两端的电压为：

由式（3）和式（6）可以求出晶闸管导通截止前后断路器下游侧故障相间电压变化为：

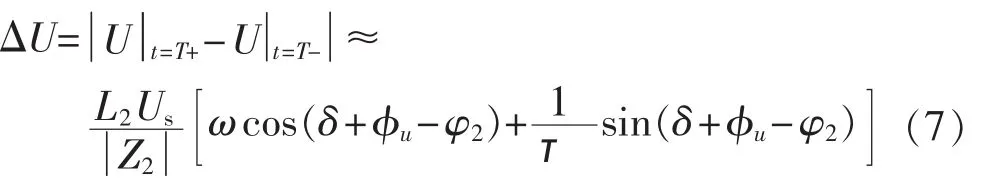
由于晶闸管截止瞬间流过其电流为0，因此可以得出导通角δ、负载阻抗角φ2、触发角φu之间的关系如式（8）所示［15］。

在可控触发角φu的合理取值范围（通常为90°≤φu≤150°）内，可使得 e-T/τ≈0。 此时有：

将式（9）代入式（7）可以得到：

由式（10）可以看出，在晶闸管关断瞬间，由于i1、i2随时间的变化率（即 di1/dt、di2/dt）发生变化，导致端口电压U发生幅值约为Ussin φ2的突变。图4给出了在不同的晶闸管触发角下，该电压突变量（标幺值）与Z2支路负载阻抗角的关系。

图4 不同触发角下ΔU与负载阻抗角关系Fig.4 Relationship between ΔU and impedance angle for different firing angles

从图4中可以看出：电压突变量ΔU随着晶闸管触发角的减小而增大，因此可以通过人为减小触发角来增大ΔU以便于检测；电压突变量ΔU随着阻抗角φ2的减小而减小，即使在阻抗角φ2≈8.1°（功率因数约为0.99）时，在选取触发角为90°的情况下，仍能保证产生足够大的电压突变量ΔU（约为0.1 p.u.）以被检测到。

事实上，部分补偿电容器带有失电保护功能［16］，而低压侧电容器也通常由晶闸管无暂态投切。当线路停电后，这部分电容器会因失电而立刻退出，导致负荷功率因数下降（阻抗角φ2增大），从而有利于电压突变的检测。

（2）开关闭合，有故障情况。

由于旁路故障电阻RF的存在，di1/dt和di2/dt在晶闸管关断过程中不会突变，端口电压U也不会产生突变。所以，故障情况下断路器下游侧电压在晶闸管关断前后的变化为：

比较式（10）和式（11）可知，在借助晶闸管给停电线路故障相间施加瞬时电压时，若故障已经消失，则断路器下游侧故障相间电压在晶闸管关断前后会发生明显的突变；若故障仍存在，则断路器下游侧故障相间电压在晶闸管关断前后不会发生明显的突变。因此，可根据晶闸管关断瞬间断路器下游侧故障相间检测的电压是否发生突变来区分是否存在故障。

1.3 电压突变检测

1.3.1 检测方法

现有的波形突变检测方法有多种，如短时傅里叶变换、希尔伯特-黄变换、小波变换等，其中小波变换具有时间-频率窗口可变的特点，对于高频信号具有较好的时间分辨率，对于低频信号具有较好的频率分辨率，因此，其广泛应用于信号的突变检测。

假设 x（t）为定义在 L2（R）空间上的信号，R 为连续实数集。如果信号满足条件：

则信号x（t）的小波变换为：

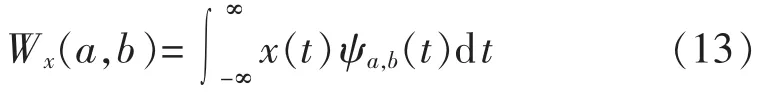
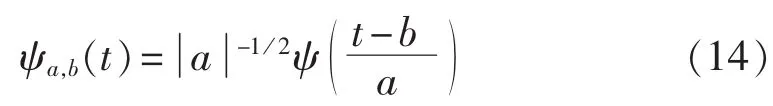
其中，ψ（t）为母小波函数；a，bєR，a≠0。

在众多小波中，Daubechies小波具有较好的扩展性，可比较灵活地权衡增加直接长度带来的边界问题，其中，db4、db5、db6小波适合用于检测短时快速的信号变化，db8、db10小波适合用于检测缓慢的信号变化［17］。本文选用db5小波对断路器下游侧故障相间电压进行小波分析，d1层分解即可得到突变信息。

1.3.2 阈值设置

基于1.2节的理论分析，电压波形突变的大小受系统参数及晶闸管触发角等诸多因素影响，突变的幅值越小就越难以检测，因此本文对停电线路无故障状态下所产生的含有极小突变的电压波形进行小波分析，根据该分析结果设定阈值。

停电线路无故障状态下测量点电压突变前、后表达式分别如式（3）和式（6）所示，其中逆变电源的幅值Us已知，而负载阻抗Z2、晶闸管的触发角φu和负载阻抗角φ2未知。

（1）负载阻抗Z2的获取。

Z2可通过施加在无故障停电线路上的激励电压和响应电流间的线性关系计算获得，并作为历史数据保存。对于图5所示无源线性系统，通过控制晶闸管对其施加激励电压 du（t）产生响应电流 di（t），基于du（t）和 di（t）在频域内的线性关系可获得其在各次频率下的等效阻抗。设dU（ω）和dI（ω）分别为暂态电压、电流信号 du（t）和 di（t）经傅里叶变换后角频率为ω的分量，则无源线性系统在角频率ω下的等效阻抗 Z（ω）为［18］：

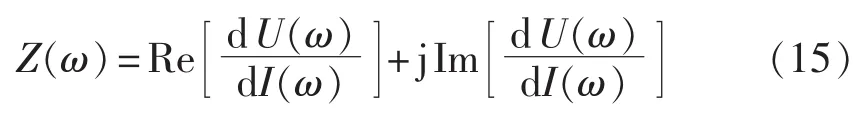
图5 系统阻抗测量原理图Fig.5 Schematic diagram of system impedance measuring

（2）φu和 φ2的确定。

根据1.2节的分析，如图4所示，在逆变电源幅值 Us确定、触发角 φu在 90°～150°之间时，电压突变量的大小与负载阻抗角φ2成正比，与晶闸管触发角φu成反比。基于这一关系，本文对负载阻抗角φ2=2.56°（负载功率因数为0.999）、触发角φu=150°这一极端情况下含有极小突变的电压波形进行小波分析，进而根据分析结果确定阈值。

（3）阈值的确定。

负载阻抗Z2、晶闸管的触发角φu和负载阻抗角φ2确定之后，代入式（3）和式（6）可得到极端情况下无故障停电线路在晶闸管关断前、后测量点处的电压波形。对其进行小波变换，根据小波变换的结果计算如式（16）所示的参数作为阈值。

其中，n为电压波形采样点个数；σ为小波分解后d1层系数的标准方差。

式（16）通常被用于波形去噪，能有效地区分出波形中的有效信息与噪声［19］。在对含有突变的电压波形进行小波分析时，突变时刻的小波检测结果为有效信息。因此，由式（16）计算出的值能够准确区分突变的存在与否。而且，该值是在上述选取的极端情况（即突变量极小的情况）下计算出来的，非极端情况下电压波形突变处的小波变换结果都要明显大于该阈值，因此可将该值作为电压波形突变检测的阈值。

需要指出的是，由于晶闸管的触发角人为可控，因此根据图4所示电压突变量ΔU与触发角的关系，还可以通过调小触发角来增大电压突变量ΔU，从而使得电压突变量的检测更为容易。从这个角度而言，本文设定的阈值是完全可以满足要求的。

综上所述，本文方法的阈值设置流程见图6。

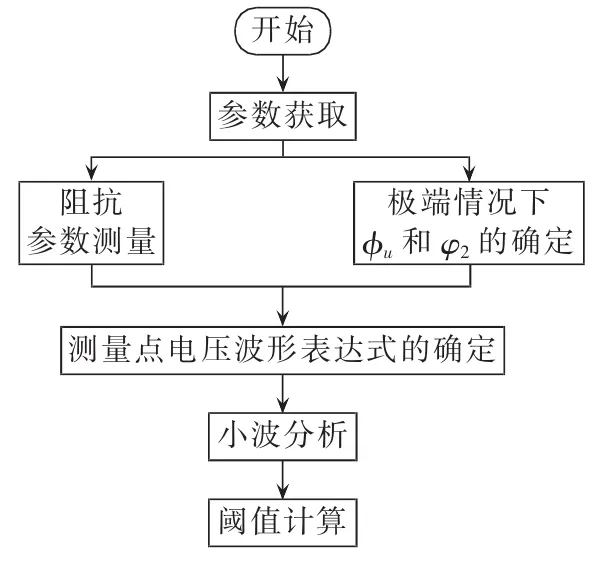
图6 阈值计算流程图Fig.6 Flowchart of threshold calculation

2 仿真验证

为检验上述判据的有效性，利用仿真加以验证。仿真所用10 kV配电网见图1，线路停电后负载为0.4 MV·A，其中并联RLC负载0.2 MV·A，电机负载0.2 MV·A，总功率因数0.95，每个周期采样256个点。

馈线在2.5 s时因AB相间发生短路故障而停电，0.5 s之后对故障相间施加瞬时高压。图7给出了在晶闸管导通角为120°时，无故障与故障情况下的断路器下游侧故障相间电压波形。从图中可以看出，没有故障时，断路器下游侧故障相间电压波形在晶闸管关断前、后存在明显的突变；而故障存在时，则不会产生明显的电压突变，结果与理论分析一致。

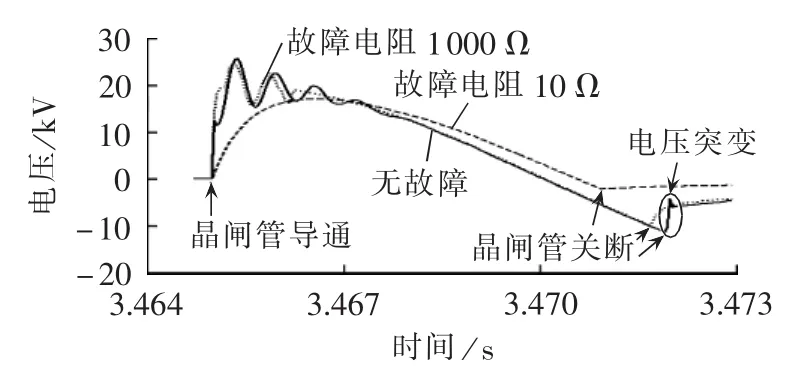
图7 不同故障情况下故障相间电压波形Fig.7 Inter-phase voltage waveform for different fault conditions

2.1 不同负载功率因数下的仿真结果

无故障（负载功率因数 cos φ2分别为 0.5、0.75、0.99）和故障电阻为50 Ω情况下断路器下游侧故障相间电压波形及其小波检测结果如图8所示。其中图 8（a）为测得的电压波形，图 8（b）、（c）、（d）为 3 种不同功率因数下的小波检测结果。从图中可以看出，随着功率因数的提高，电压突变量逐渐减小；3种功率因数无故障情况下的小波分析结果均能够准确识别出电压突变；仿真结果与理论分析一致，验证了理论分析建立的电压突变判据的有效性。

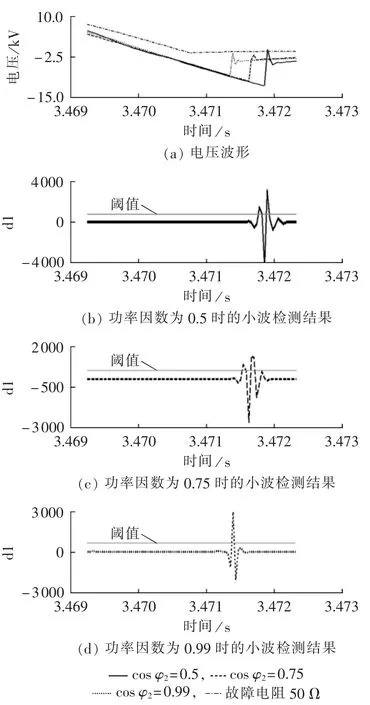
图8 φu=120°时，不同功率因数下电压波形及小波检测结果Fig.8 Voltage waveform and wavelet detection result for different power factors，when φu=120°

2.2 不同触发角下的仿真结果

无故障（触发角分别为 90°、120°、150°）和故障电阻为50 Ω情况下断路器下游侧故障相间电压波形及其小波检测结果如图9所示。其中图9（a）为不同情况下测得的电压波形，图 9（b）、（c）、（d）分别为3种不同触发角情况下测得的电压波形的小波分析结果。从图中可以看出，触发角增大后，尽管电压突变量有所减小，但是无故障情况下的电压突变量仍然较大，小波检测结果准确，从而验证了电压突变判据的有效性。

3 模拟实验

为了对所提方法在实际使用中的效果进行检验，进一步检验理论判据的有效性，进行了模拟实验。模拟实验平台具体实验接线图如图10所示。

模拟实验中共有2条馈线，电压等级为220V，停电后剩余负荷参数为：1号馈线阻感负载R1=43.5 Ω、L1=66.8 mH，电动机负载 3 kV·A、功率因数 0.9；2号馈线阻感负载R2=29.0 Ω、L2=44.5 mH，电动机负载6 kV·A、功率因数 0.9。

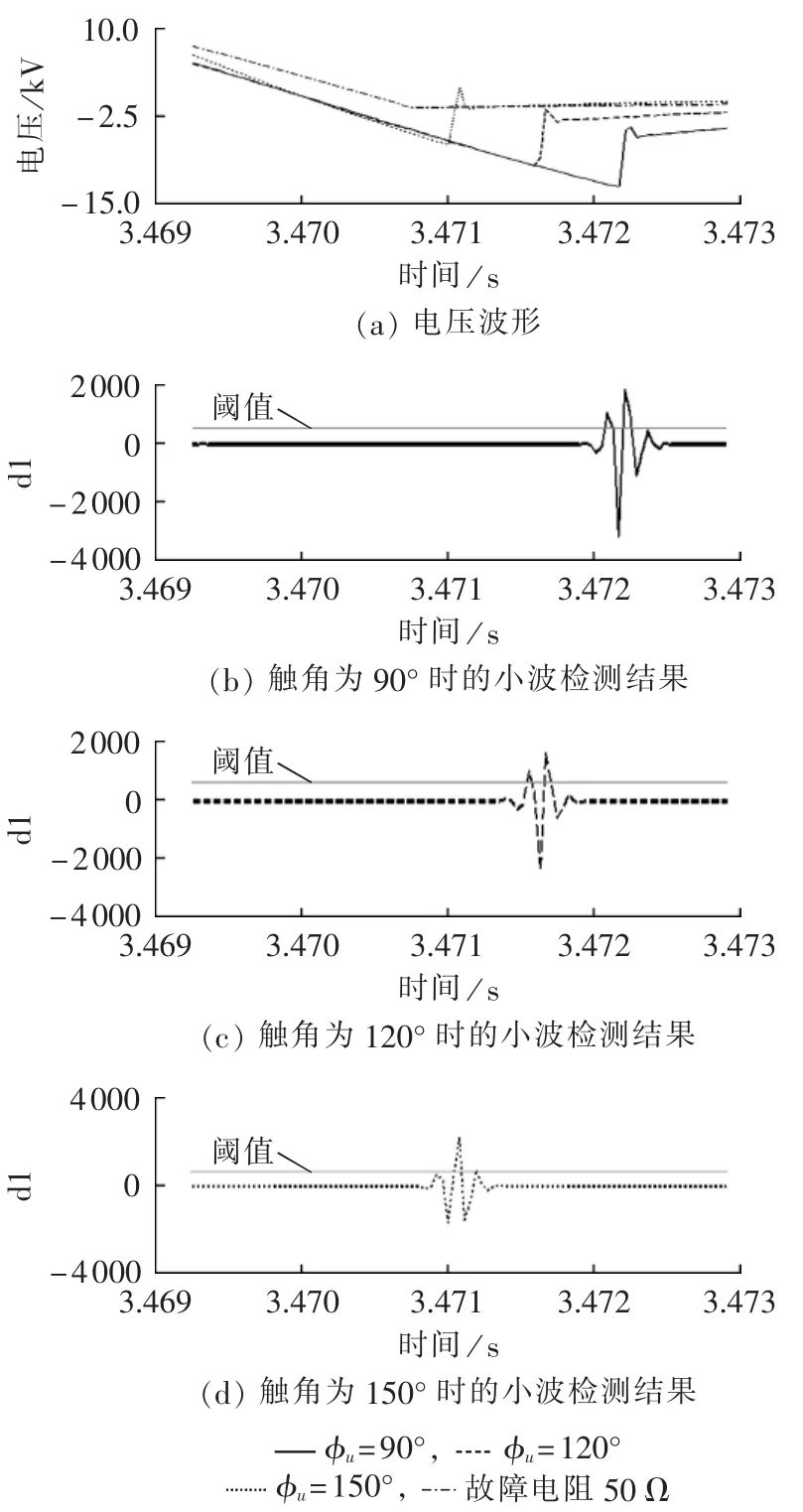
图9 cos φ2=0.95时，不同触发角下电压波形及小波检测结果Fig.9 Voltage waveform and wavelet detection result for different firing angles，when cos φ2=0.95

图10 模拟实验接线图Fig.10 Wiring diagram of simulation experiment

模拟实验根据该系统在不同故障电阻和不同晶闸管触发角度等情况下进行验证，图11给出了故障电阻分别为15.6 Ω和156 Ω、晶闸管触发角为120°情况下，AB相发生相间短路故障的实验结果。

模拟实验的结果显示，在不同故障电阻下，无故障情况下的电压突变量要远大于故障情况下的电压突变量，可利用该判据有效地检测出故障是否存在。

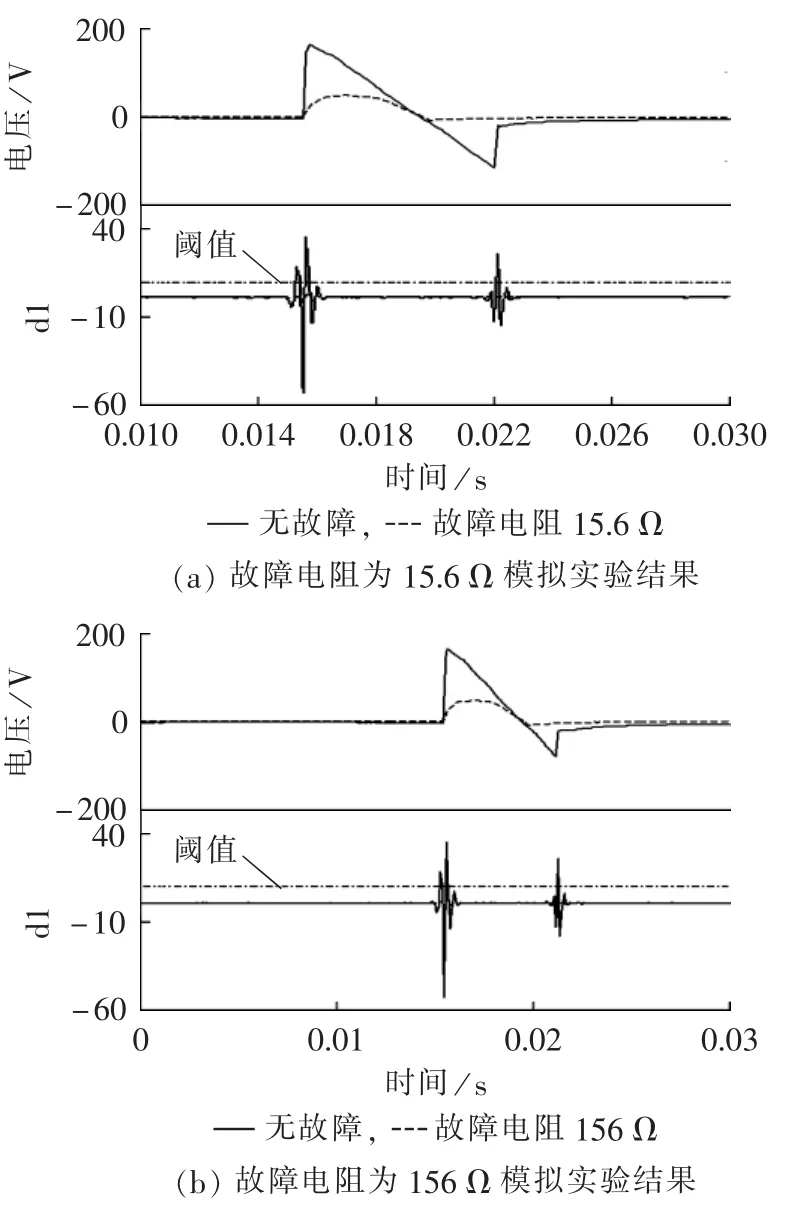
图11 模拟实验仿真结果Fig.11 Simulation experiment results

4 结论

本文针对我国配电线路重合闸以及尝试性送电的盲目性，提出了一种停电线路相间故障自动检测技术，即利用电力电子开关器件通过配电变压器向停电线路故障相间施加瞬时高压，根据断路器下游侧端口处检测到的电压波形来区分馈线相间是否还存在故障，进而指导断路器是否进行合闸操作。该方法不需要通信，理论计算、仿真以及模拟实验都验证了该方案的有效性，为解决我国停电线路相间故障检测问题提供了一种全新的思路。

［1］刘洪顺，李庆民，邹亮，等.安装故障限流器的输电线路潜供电弧特性与单相重合闸策略［J］.中国电机工程学报，2008，28（31）：62-67.LIU Hongshun，LIQingmin，ZOU Liang，etal.Secondary arc characteristics and single-phase autoreclosure scheme of EHV transmission line with fault current limiter［J］.Proceedings of the CSEE，2008，28（31）：62-67.

［2］林达，王庆庆，王慧芳，等.带并联电抗器同杆双回线自适应重合闸方案［J］.电力系统自动化，2015，39（6）：101-106.LIN Da，WANG Qingqing，WANG Huifang，et al.Adaptive reclosure scheme for parallel lines with shunt reactors［J］.Automation of Electric Power Systems，2015，39（6）：101-106.

［3］李斌，李永丽，黄强，等.单相自适应重合闸相位判据的研究［J］.电力系统自动化，2003，27（22）：41-44.LI Bin，LI Yongli，HUANG Qiang，et al.Study on phase criterion for single-pole adaptive reclosure［J］.Automation of ElectricPower Systems，2003，27（22）：41-44.

［4］李斌，李永丽，盛鹍，等.带并联电抗器的超高压输电线单相自适应重合闸的研究［J］.中国电机工程学报，2004，24（5）：56-60.LI Bin，LI Yongli，SHENG Kun，et al.The study on single-pole adaptive reclosure of EHV transmission lines with the shunt reactor［J］.Proceedings of the CSEE，2004，24（5）：56-60.

［5］王增平，刘浩芳，徐岩，等.基于改进型相关法的单相自适应重合闸新判据［J］.中国电机工程学报，2007，27（10）：49-55.WANG Zengping，LIU Haofang，XU Yan，et al.A new criterion for single-phase adapative automatic reclosure based on improved correlation algorithm［J］.Proceedings of the CSEE，2007，27（10）：49-55.

［6］DJURIC M B，TERZIJA V V.A new approach to the arcing faults detection for fast autoreclosure in transmission systems［J］.IEEE Transactions on Power Delivery，1995，10（4）：1793-1798.

［7］索南加乐，邵文权，宋国兵.基于参数识别的单相自适应重合闸研究［J］.中国电机工程学报，2009，29（1）：48-54.SUONAN Jiale，SHAO Wenquan，SONG Guobing.Study on single-phase adaptive reclosure scheme based on parameter identification［J］.Proceedings of the CSEE，2009，29（1）：48-54.

［8］邵文权，宋国兵，索南加乐，等.带并联电抗器输电线路三相自适应重合闸永久性故障判别［J］.中国电机工程学报，2010，30（4）：91-98.SHAO Wenquan，SONG Guobing，SUONAN Jiale，et al.Identification of permanent faults for three-phase adaptive reclosure of the transmission lines with shunt reactors［J］.Proceedings of the CSEE，2010，30（4）：91-98.

［9］曹芬，何奔腾.带并联电抗器的超高压输电线路单相自适应重合闸新算法［J］.电力系统自动化，2009，33（23）：55-59.CAO Fen，HE Benteng.New algorithm for single-phase adaptive reclosure of EHV transmission lines with shunt reactor［J］.Automation of Electric Power Systems，2009，33（23）：55-59.

［10］索南加乐，梁振锋，宋国兵.采用模量参数识别的三相重合闸永久性故障判别原理［J］.中国电机工程学报，2010，30（25）：81-86.SUONAN Jiale，LIANG Zhenfeng，SONG Guobing.Permanent faults identification based on mode component for three-pahse autoreclosing on transmission lines with shunt reactors［J］.Proceedings of the CSEE，2010，30（25）：81-86.

［11］LONG Xun，XU Wilsun，LI Yunwei.A new technique to detect faults in de-energized distribution feeders-part I：scheme and asymmetrical fault detection［J］.IEEE Transactions on Power Delivery，2011，26（3）：1893-1901.

［12］LONG Xun，LI Yunwei，XU Wilsun，et al.A new technique to detect faults in de-energized distribution feeders-part Ⅱ：symmetrical fault detection［J］.IEEE Transactions on Power Delivery，2011，26（3）：1902-1910.

［13］WILSON D D，H E DMAN D E.Fault isolator for electrical utility distribution systems：4370609［P］.1983-01-25.

［14］李永丽，李斌，黄强，等.基于高频保护通道信号的三相自适应重合闸方法［J］.中国电机工程学报，2004，24（7）：78-83.LI Yongli，LI Bin，HUANG Qiang，et al.The study on threepahse adaptive reclosure based on carrier channel and signal transmission［J］.Proceedings of the CSEE，2004，24（7）：78-83.

［15］陈坚.电力电子学——电力电子变换与控制技术［M］.2版.北京：高等教育出版社，2004：143-148.

［16］刘萍.电力电容器的保护与运行［J］.科技资讯，2010（18）：136.

［17］王晶，束洪春，陈学允.小波变换电力系统学应用综述［J］.电网技术，2003，27（6）：52-62.WANG Jing，SHU Hongchun，CHEN Xueyun.A survey of wavelets transform applying to power system engineering ［J］.Power System Technology，2003，27（6）：52-62.

［18］潘学萍，扈卫卫，尚霏.多信号模态参数识别的小波方法［J］.电力自动化设备，2013，33（5）：31-36.PAN Xueping，HU Weiwei，SHANG Fei.Wavelet analysis based modal parameter identification from multiple signals［J］.Electric Power Automation Equipment，2013，33（5）：31-36.

［19］SANTOSO S，POWERS E J，GRADY W M.Electric power quality disturbance detection using wavelet transform analysis［C］∥Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis，1994.Philadelphia，PA，USA：IEEE，1994：166-169.