基于有限元法探究电力变压器绕组变形频率响应的仿真研究

邹 林 ，廖一帆 ，罗 兵 ，赵仲勇 ，陈晓晗 ，3，姚陈果

（1.南方电网科学研究院，广东 广州 510080；2.重庆大学 电气工程学院 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；3.国网冀北电力有限公司廊坊供电公司，河北 廊坊 065000）

0 引言

电力变压器是电力系统中最重要的电气设备之一，其健康状态对于整个电网的安全运行具有重大意义［1］，而绕组变形为最常见的变压器故障类型之一。绕组的轻微变形不易被发现，并且变形具有累积效应。随着绕组变形的加剧，一旦发生外部短路，可能会造成绕组发生严重变形，损坏变压器。因此，及时准确地检测绕组变形十分必要。

目前，在检测绕组变形的电测法领域，专家学者们提出了两大类方法：一类是基于测量绕组的电阻、电容和电感等参数，通过分析参数改变确定绕组的变形情况，主要包括短路阻抗法、电容量变化法和直流电阻变化法等［2-3］；另一类是通过分析绕组响应特性确定绕组的变形情况，主要有低压脉冲法、频率响应分析法和传输函数法等［4-5］。变压器绕组变形检测的电测法中，短路阻抗法需动用庞大的实验设备，且费时、费力，灵敏度不高，难以保证测量精度，在现场使用有困难［6］；电容量变化法受绕组本身电容的影响，对鼓包、扭曲等故障的测试灵敏度较差［7］；低压脉冲法在间隔较长时间时，重复性差，且对变压器绕组的首端故障不灵敏［8］；频率响应分析法与以上各种方法相比，具有试验设备简单轻巧、测试灵敏度高、实验图谱分析直观、数据量值分析具有可比性等优越性［9］。因此，频率响应分析法被认为是具有良好应用前景的检测手段。

在分析绕组变形引起频率响应变化的机理时，国内外研究人员采用多种方式进行探究，其中最为常见的辅助手段是采用等值电路模型探究绕组变形与频率响应的关系［10-14］。这些研究工作对于理解频率响应意义重大，但是目前该领域还存在许多亟待解决的问题。例如，变压器绕组的电路模型中的电容、电感参数一般采用解析公式法进行计算，而解析公式法是基于理想的电磁场分布推导，仅适用于健康绕组，对不规则形状的变压器变形绕组难以计算其电路参数；在已有的变压器绕组变形频率响应曲线的仿真研究中，往往依靠经验单一改变电路参数中的电容或电感等模拟不同类型的绕组变形，而实际中某些变形类型并非仅引起单一参数的变化。本文将针对这些问题进行探讨。

有限元技术是近年来迅速发展的一种求解偏微分方程边值问题的数值手段，其能够较为精确地求解不规则物体的电磁特性，或许能够用于解决上述问题。综上所述，本文首先将利用有限元法求取健康绕组的等值电路参数，并通过与传统解析公式法的计算值对比验证有限元建模与计算的正确性；然后，通过有限元法获取各种变形绕组的电路参数，寻求绕组变形对电容、电感参数的影响规律；最后，在电路仿真软件中建立变压器绕组等值电路模型，结合频率响应分析法，在绕组的一端施加扫频信号，另一端获得响应信号，进而得到不同绕组变形下的频率响应曲线，探究绕组变形对频率响应曲线谐振点频率和幅值变化的影响。

1 变压器绕组的等值电路模型

电力变压器在较高频率（通常指1 kHz以上）电压的作用下，铁芯的磁导率几乎与空气的磁导率一样，绕组可以看作一个由线性电阻、电感、电容等组成的无源线性分布参数网络［15-17］，以图1所示的连续式绕组部分为例。为了便于计算，常用集总参数代替分布参数，由于电阻对电位分布的影响很小，故常忽略电阻的影响，简化后的等值电路模型是一个具有电容和电感的集总参数链型网络，如图1（b）所示。

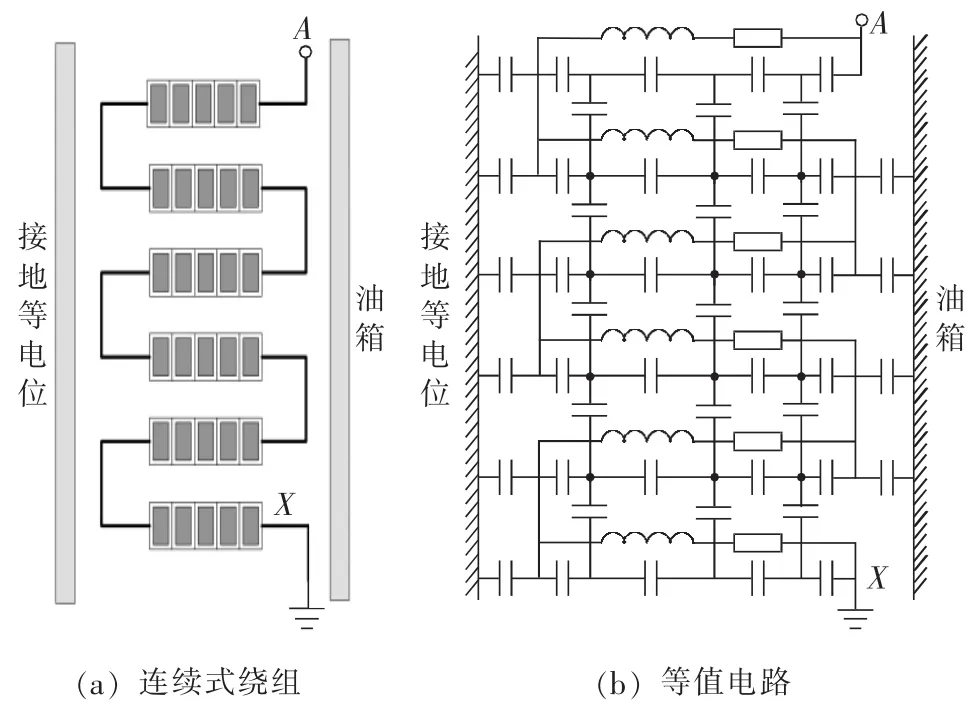
图1 连续式绕组模型Fig.1 Model of continuous winding

对图1中的电路划分单元时，令高压绕组以上、下两饼为一个单元，其中每个单元都有一个等值纵向电容K、电感L以及对地电容C。设定低压绕组、铁芯和油箱三部分作为接地零电位。绕组的等值电路可以简化为图2。图中，对地电容C包含高低压绕组间以及高压对油箱两部分电容；Uin、Uout分别为输入、输出电压；Ri、Ro分别为输入、输出电阻。

图2 绕组简化等值电路Fig.2 Simplified equivalent circuit of winding

2 基于有限元法的健康绕组等值电路参数计算

仿真采用ANSYS Maxwell有限元软件，电力变压器的型号为SF10-40000/110，变压器的相关尺寸及介质材料参数如表1—3所示。

电力变压器绕组的几何电容包括径向几何电容和轴向几何电容。轴向几何电容包括绕组线匝之间的匝间电容、线饼之间的饼间电容；径向几何电容包括绕组与铁芯之间的电容、绕组与绕组之间的电容和绕组与油箱之间的电容。

2.1 等值纵向电容的计算

2.1.1 匝间电容的计算

首先建立变压器连续式绕组的三维双饼模型如图3所示，其中匝绝缘介电常数为2.6，单个线饼匝数为18匝。对线饼中的线匝进行编号：上层各匝导线从左往右依次编号为 c1、c2、…、c17、c18，下层各匝导线从右往左依次编号为 c19、c20、…、c35、c36。 采用静电场求解器求解电容参数矩阵，部分匝间电容计算结果见表4。

表1 变压器尺寸数据Table1 Dimensional data of transformer

表2 高压连续式绕组尺寸数据Table2 Dimensional data of HV continuous winding

表3 绝缘材料的相对介电常数Table3 Relative dielectric constants of insulation materials

图3 电力变压器绕组的电容组成Fig.3 Composition of power transformer winding capacitance

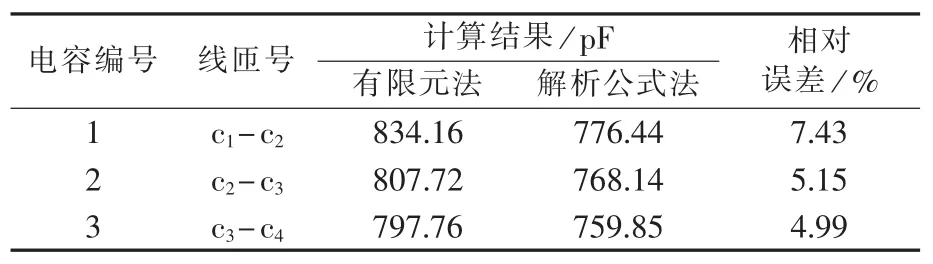
表4 连续式绕组的部分计算匝间电容Table4 Part of calculated inter-turn capacitances of continuous winding

为了验证有限元法计算匝间电容的正确性，采用解析公式法计算绕组线饼的匝间电容。考虑到线匝的宽度远远小于变压器线圈的平均直径，因此匝间几何电容Cw（pF）可以通过平行板电容的计算原理得到，如式（1）所示，部分匝间电容计算结果如表4所示。

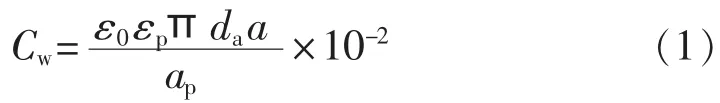
其中，ε0为空气介电常数；da为线圈平均直径（mm）；ap为匝绝缘厚度（mm）；a 为裸导线高（mm）；εp为匝绝缘相对介电常数。

图4显示了单饼18匝形成匝间电容的有限元法计算值和解析公式法计算值的分布。由图可见，两者结果较为一致，表明有限元法建模与计算的正确性。另外，有限元法得到的匝间电容大于解析公式法所得结果，其相对误差的范围为3.16%～8.34%。有限元法和解析公式法求得的匝间电容平均值分别为748.16 pF、710.17 pF。这主要是因为解析公式法是基于电场分布均匀这一前提，没有考虑到线匝的边缘效应，仅求解2个相邻匝之间的电容而不考虑周围电场的影响，而实际中匝间电场的分布并不均匀，并且匝间电容的求解会受到其他匝产生的电场的影响。

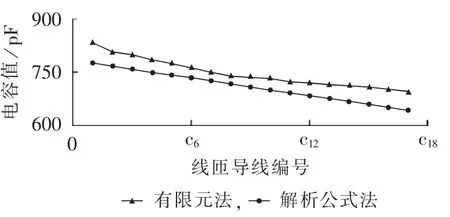
图4 连续式绕组匝间电容计算值的分布Fig.4 Distribution of calculative inter-turn capacitances of continuous winding

2.1.2 饼间电容的计算

绕组的饼间电容计算模型如图5所示，线饼间的介电常数采用复合绝缘等值介电常数2.76，此复合绝缘等值介电常数由油道等值介电常数和匝绝缘等值介电常数计算所得，由于篇幅限制，在此不再赘述［18］。利用有限元软件计算出高压绕组上、下线饼各对应匝间的电容值后相加即为饼间电容，将所有线饼之间的饼间电容取平均值即可得到饼间电容的有限元法计算值为1603.49 pF。

图5 连续式绕组的三维双饼模型Fig.5 3D model of dual-disk continuous winding

采用解析公式法计算绕组的饼间电容，由于线匝的宽度远远小于变压器线圈的平均直径，因此饼间几何电容Cs（单位为pF）依然采用平行板电容的计算原理，如式（2）所示。采用解析公式法得出的饼间电容为1498.33 pF。

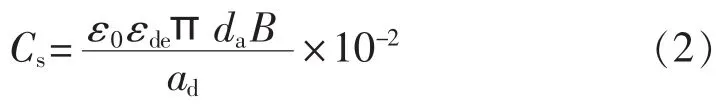
其中，ad为饼间绝缘厚度（mm）；B为线饼宽度（mm）；εde为饼间绝缘的等值相对介电常数。

有限元法和解析公式法计算结果较为接近，验证了仿真的正确性。另外，饼间电容有限元法的计算结果大于解析公式法的计算结果，两者之间的误差为7.02%。这是因为饼间电容的解析公式求解同样是基于饼间电场分布均匀且忽略线饼厚度的前提，而实际中考虑到边缘效应饼间电场的分布并不均匀。

2.1.3 等值纵向电容的计算

计算得到绕组的匝间电容和饼间电容后，便可计算绕组等值电路中的等值纵向电容。等值纵向电容为集总电容，它等值于分布参数推导的结果，由绕组饼间和匝间的静电能量决定。等值纵向电容可通过电容的静电能量计算，以连续式绕组中的2个线饼为例，计算公式如式（3）所示［18］。

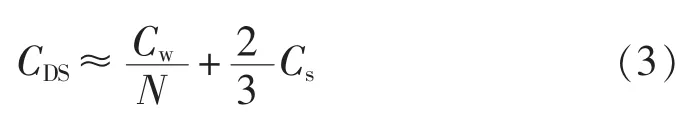
其中，CDS为等值纵向电容；N为线饼匝数。

由于匝间静电能量较小，等值纵向电容主要由饼间静电能量决定。根据式（3）计算得到的等值纵向电容为1089.78 pF，大于解析公式法的计算结果（1018.61 pF），相对误差为 6.99%。

2.2 等值对地电容的计算

高压绕组的对地电容计算模型如图6所示，高、低压绕组间采用复合绝缘等值介电常数2.42，此复合绝缘等值介电常数由绝缘纸筒、油隙、绕组内外侧匝绝缘的等值介电常数计算所得，由于篇幅限制 ， 在 此 不 再 赘 述［18］。高压绕组与油箱之间的等值介电常数为变压器油介电常数2.2，对仿真得出的所有高压绕组线饼的对地电容求取平均值，即可获得变压器绕组单个高压绕组线饼的对地电容值。等值对地电容的计算结果如表5所示。

图6 连续式绕组线饼、铁芯和油箱模型Fig.6 Model of continuous winding disks，iron core and fuel tank

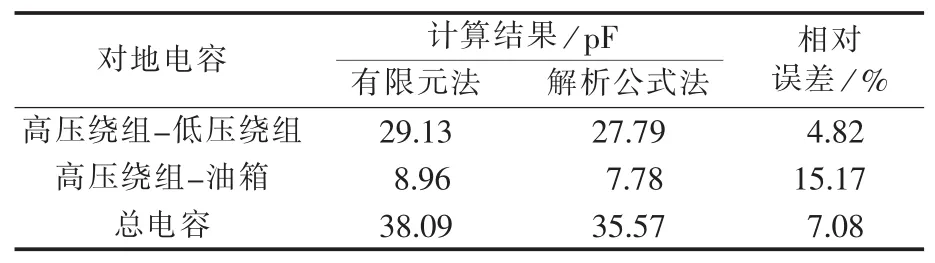
表5 连续式绕组的对地电容Table5 Capacitances between continuous winding and ground

采用解析公式法计算高压绕组的对地电容，若变压器油箱的外形接近于圆筒形，则主要按照同轴圆柱电容公式计算，如式（4）所示。

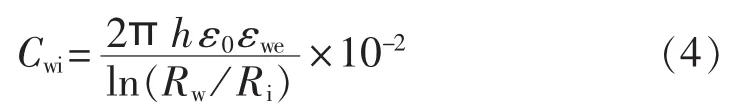
其中，Cwi为高压绕组的对地电容；εwe为变压器油的等值介电常数；h为绕组的轴向高度（mm）；Rw为油箱内半径（mm）；Ri为绕组外半径（mm）。

考虑到同轴圆柱电容计算公式的应用条件是h≫Rw-Ri，故计算时需将绕组等效为圆柱结构，将得出的结果除以单元数。解析公式法的计算结果如表5所示。

有限元法和解析公式法的计算结果较为接近，验证了有限元计算的正确性。对地电容有限元法的计算结果大于解析公式法的计算结果，这可能受到线圈端部电场分布不均匀的影响；另外解析公式法的求解基于完全平行分布的理想电场，而实际上即使是不正对的面同样会产生电容，解析公式法无法考虑不正对的面产生的部分电容，故有限元法得到的对地电容值略大。

2.3 等值电感的计算

由于变压器绕组频率响应频段内，铁芯的作用可以忽略，因此，采用静磁场求解器求解空心线圈的电感矩阵。建立的模型与图5相似，在此不再赘述。对每个线饼求解自电感，再求平均值，可得到单饼自感值。

同时采用空心线圈的电感计算公式进行计算，考虑到线圈平均直径远大于单元线饼厚度，故通过平面线圈的电感公式计算自感，如式（5）所示。

其中，L0为电感值；d为线圈平均直径（mm）；w为线饼匝数；μ0为真空磁导率；ψ是和B/d相关的函数，B为线饼宽度（mm）。

有限元法和解析公式法的计算结果分别为521.8 μH 和 594.1 μH，较为接近，验证了仿真的正确性。另外，两者之间存在误差12.17%，这是由于解析公式法忽略了绕组单元线饼的厚度，并且该公式基于均匀分布的磁场计算，而实际磁场并非均匀分布。

3 基于有限元法的变形绕组等值电路参数计算

由第2节有限元法仿真结果和解析公式法计算结果对比可知，有限元法的建模过程与计算结果正确无误。同时，考虑到解析公式法的建立原则是基于电磁场均匀分布的假设且忽略了绕组的部分参数，采用有限元法的计算结果显然更为精确。

值得一提的是，目前的解析公式法仅适用于计算健康绕组的等值电路参数，而对于变形绕组或不规则绕组的参数计算，显得无能为力；另外，通过有限元计算可以获知绕组变形同时对电容、电感而非某单一参数的影响，改变过去电路仿真依靠经验更改单一电路参数的随意性。因此本节利用有限元法求取绕组不同变形类型和变形程度的电路参数，获得等值电路参数变化的规律。开展的绕组变形仿真类型主要包括常见的绕组轴心偏移、绕组辐向变形和绕组饼间间距变化。

3.1 绕组轴心偏移

目前110 kV变压器主要采用三相三柱式结构，但是三相绕组并非对称排列，尤其对于A相和C相绕组，在B相绕组电流引起的磁场作用下，易造成铁芯柱两侧磁场分布不均，导致绕组垂直于铁芯柱单侧受力，进而发生绕组的轴心偏移。

利用ANSYS Maxwell有限元软件建立变压器的轴心偏移模型，以高压绕组向右偏移35 mm为例，图7显示了高压绕组轴心向右偏移的俯视图。

图7 高压绕组轴心偏移35 mm后的变压器俯视图Fig.7 Top view of power transformer with 35 mm central displacement of HV winding

对健康绕组和高压绕组轴心偏移35 mm 2种情况进行仿真。绕组轴心偏移后，变压器等效电路模型中的参数发生改变，其中主要是对地电容改变，如表6所示。高压绕组轴心偏移后的模型单元对地电容与未变形时相比增大，增幅为126.41%。其中高低压绕组间的电容变化较大，变化量高达164.68%；由于高压绕组与油箱之间的距离比较远，因此两者间的电容受轴心偏移的影响很小，变化量仅为2%。

表6 高压绕组轴心偏移35 mm后高压绕组与油箱间电容及高压绕组与低压绕组间电容的变化Table6 Change of capacitance between HV winding and ground due to 35 mm central displacement of HV winding

在模型中设置高压绕组偏移5～35 mm，以5 mm为步长，共设置6个偏移量，得到模型单元对地电容的变化结果如图8所示。可见随着轴心偏移量的增加，对地电容增大，且轴心偏移量越大则对地电容的增长速度越快。

3.2 绕组辐向变形

由于线饼上各点磁场分布不同，绕组中一个线饼的各点会受到不同电磁应力作用，线饼可能会同时受到大小不等的扩张力和内缩力。在这2种力的共同作用下，如果受力超过线圈刚度的屈服点，将导致线饼发生永久变形，即经常见到的梅花状或鼓包状绕组变形现象。

图8 高压绕组轴心偏移对对地电容的影响Fig.8 Curve of capacitance between HV winding and ground vs.central displacement of HV winding

利用有限元软件建立变压器的辐向变形模型。图9为高压绕组辐向变形俯视图，变形程度体现为4类不同的辐向变形，从左到右分别设定为类别1、2、3、4。变形量体现为绕组辐向变形形变量占半径的比例，图9中绕组形变量为半径的30%。

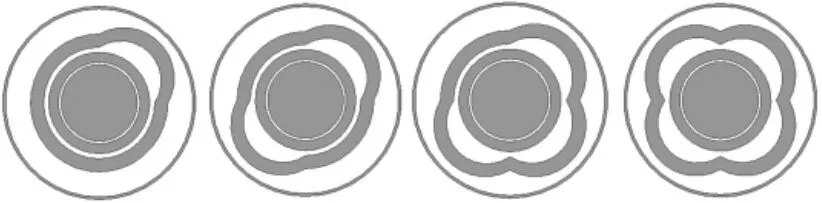
图9 高压绕组4种不同辐向变形的俯视图Fig.9 Top views of HV winding with four radial deformation types

仿真计算发现，高压绕组发生辐向变形后，其对地电容、等值纵向电容和电感均发生改变。需要说明的是，辐向变形绕组参数的计算难以通过传统的解析公式法实现。另外，辐向变形导致了等值电路模型多种参数的变化，而不是某种单一参数的改变。

设置变形类别0为未变形，仿真高压绕组的所有线饼同时出现不同变形程度和变形量的辐向变形，等值电路参数计算结果如图10—12所示。由图10可见，变形类别0到4，单元对地电容减小，但是对地电容并非随着形变量的增大而减小，这主要是因为对地电容由对低压绕组和对油箱两部分电容组成，绕组发生辐向变形后，对低压绕组电容减小，而对油箱电容增加，两者的变化量起到抵消作用。由图11、12可知，等值纵向电容和电感值均随着形变量的增加而增加，变形类别由0到4，等值纵向电容和电感值同样呈现增长的趋势。

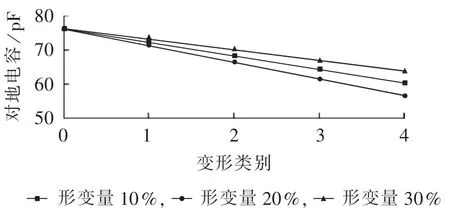
图10 高压绕组辐向变形对对地电容的影响Fig.10 Effect of HV winding radial deformation on capacitance between HV winding and ground

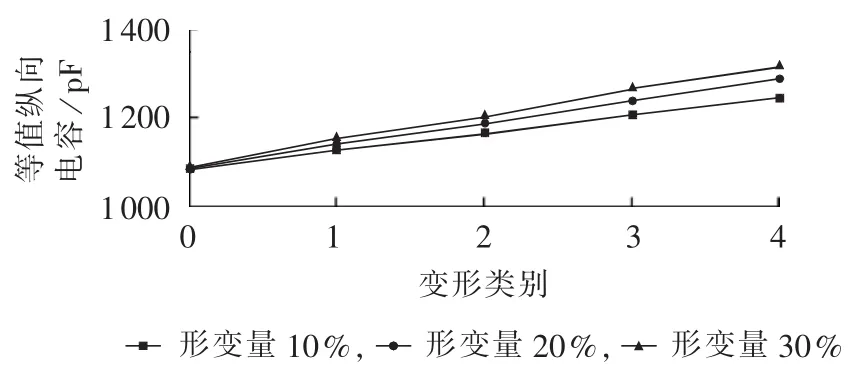
图11 高压绕组辐向变形对等值纵向电容的影响Fig.11 Effect of HV winding radial deformation on equivalent longitudinal capacitance

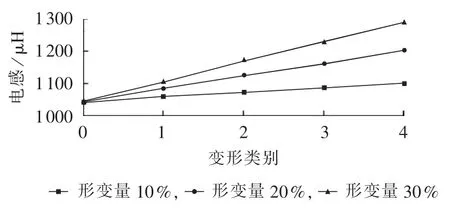
图12 高压绕组辐向变形对电感的影响Fig.12 Effect of HV winding radial deformation on inductance

3.3 绕组饼间间距变化

变压器绕组中的一个线饼除了受到垂直于铁芯轴线方向的电磁力，还会受到轴向的电磁力，若该力大于绕组的机械形变应力时，线饼就会发生上、下移动，导致绕组线饼间距变化。当该种形变比较严重时，上、下2个线饼极有可能贴合在一起，使其外绝缘油纸损坏，引起2个线饼短路，直接改变变压器变比，严重影响变压器的正常运行；与此同时，存在于线饼之间的绝缘垫片在绕组挤压和摩擦作用下会发生脱落和损坏，严重影响绕组的结构稳定性，劣化变压器的内绝缘环境［19］。

利用有限元软件建立变压器的饼间间距变化模型，其中正常变压器高压绕组的饼间间距为4.02 mm，故障后的饼间间距必定小于4.02 mm。

高压绕组饼间间距减小后，变压器等效电路模型中的参数发生改变，仿真发现，这主要是因为饼间电容形成的等值纵向电容发生改变，如图13所示。由仿真结果可知，饼间间距减小，变形绕组与未变形绕组（饼间间距4.02 mm）的饼间电容相比，饼间电容增大，进而导致单元等值纵向电容增大。

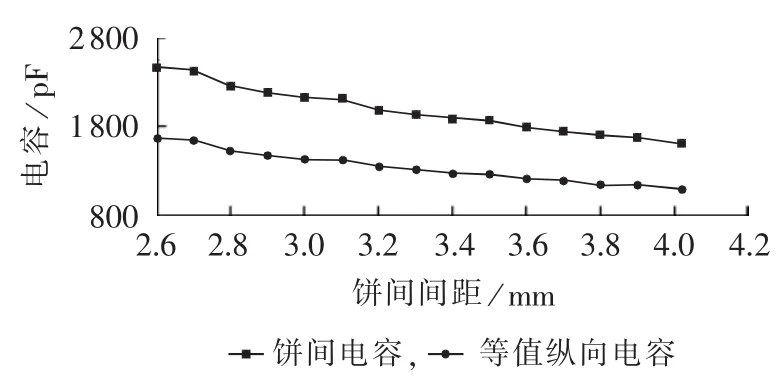
图13 高压绕组饼间间距变化对饼间电容和等值纵向电容的影响Fig.13 Effect of inter-disk distance variation on HV winding inter-disk capacitance and equivalent longitudinal capacitance

4 绕组变形对频率响应曲线影响的仿真分析

第2、3节利用有限元法仿真了健康绕组与变形绕组的等值电路参数值变化，并获得了绕组变形类别对等值电路参数的影响，本节将基于这些电路参数在PSPICE中建立电路模型进行仿真，探索变压器绕组不同变形类别和变形程度下频率响应曲线的变化特征。

按照图2在软件中建立变压器绕组以双饼为单元的等值电路模型。PSPICE仿真中输入的扫频信号源为电压源，其幅值为1 V，设定扫频方式为倍频扫频（Decade），扫频频率由 1 kHz 到 1 MHz［20］，其中每个数量级扫描点数为10000。

在等值电路模型中，根据绕组变形的类别和变形程度更改电路参数值，即可模拟绕组不同的变形情况。

4.1 绕组轴心偏移

为了研究高压绕组轴心偏移量对频率响应曲线谐振点的影响，分别绘制高压绕组7个单元在轴心偏移15 mm、35 mm情况下的频率响应曲线和正常绕组的频率响应曲线，如图14所示。可见，随着高压绕组轴心偏移量的增加，谐振波峰和谐振波谷的频率值减小，且绕组轴心偏移对频率响应曲线较低频率的谐振点频率影响较大，对较高频率的谐振点幅值影响较小。

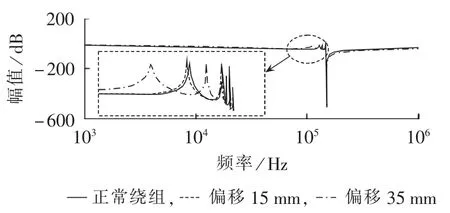
图14 高压绕组轴心偏移量对频率响应曲线的影响Fig.14 Effect of HV winding central displacement on frequency-response curve

为了研究高压绕组轴心偏移单元数对频率响应曲线的影响，分别绘制高压绕组3个单元、7个单元轴心偏移35 mm情况下的频率响应曲线和正常绕组的频率响应曲线，如图15所示。可见，轴心偏移的单元数越多，谐振点向低频方向的移动量越大。

4.2 绕组辐向变形

为了研究高压绕组辐向变形形变量对频率响应曲线的影响，分别绘制高压绕组7个单元辐向变形形变量为10%、30%（变形类别均为4）时的频率响应曲线和正常绕组的频率响应曲线，如图16所示。可见，随着高压绕组变形形变量的增加，谐振波峰和波谷的频率减小，绕组变形对所有频段内谐振点频率和幅值的影响一致，基本不存在差别。

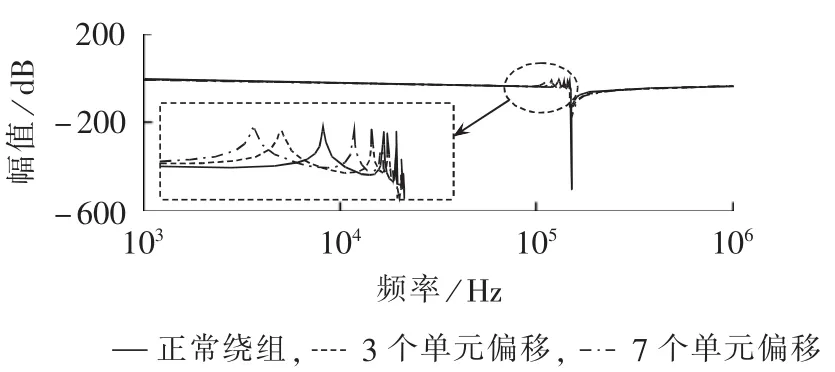
图15 高压绕组不同单元数轴心偏移对频率响应曲线的影响Fig.15 Effect of quantity of HV winding unit with central displacement on frequency-response curve

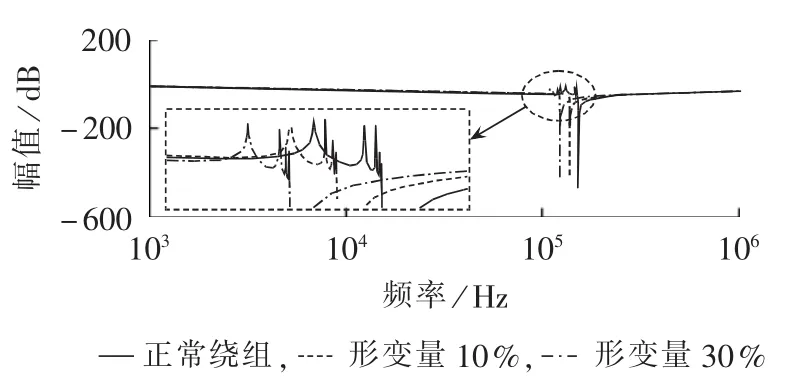
图16 高压绕组辐向变形形变量对频率响应曲线的影响Fig.16 Effect of HV winding radial deformation degree on frequency-response curve

为了研究高压绕组辐向变形程度对频率响应曲线的影响，分别绘制高压绕组辐向变形类别为2、4（形变量为30%）时的频率响应曲线和正常绕组的频率响应曲线，如图17所示。可见，高压绕组辐向变形类别由2变为4时，谐振点向低频方向的移动量增加。

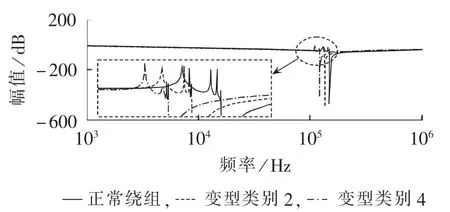
图17 高压绕组辐向变形类别对频率响应曲线的影响Fig.17 Effect of HV winding radial deformation type on frequency-response curve

为了研究高压绕组辐向变形单元数对频率响应曲线的影响，分别绘制高压绕组3个单元、7个单元辐向变形形变量为30%（变形类别为4）时的频率响应特性曲线和正常绕组的频率响应特性曲线，如图18所示。可见，辐向变形单元数越多，谐振点向低频方向的移动量越大。

4.3 绕组饼间间距变化

为了研究高压绕组饼间间距变化值对频率响应曲线的影响，绘制高压绕组7个单元饼间间距为3.4 mm、2.6 mm时的频率响应曲线和正常绕组的频率响应曲线，如图19所示。可见，随着高压绕组饼间间距的减小，谐振波峰和波谷的频率减小，且波谷的幅值基本不受绕组变形影响。

图18 高压绕组不同单元数辐向变形对频率响应曲线的影响Fig.18 Effect of quantity of HV winding unit with radial deformation on frequency-response curve

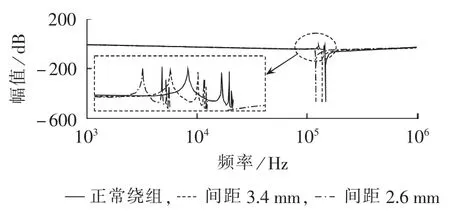
图19 高压绕组饼间间距对频率响应曲线的影响Fig.19 Effect of HV winding inter-disk distance on frequency-response curve

为了研究高压绕组饼间间距单元数对频率响应曲线的影响，分别绘制高压绕组3个单元、7个单元线饼间距2.6 mm时的频率响应曲线和正常绕组（饼间距4.02 mm）的频率响应曲线，如图20所示。可见，饼间间距减小的单元数越多，频率响应曲线向左的移动量越大。

图20 高压绕组不同单元数饼间间距减小对频率响应曲线的影响Fig.20 Effect of quantity of HV winding unit with inter-disk distance decrease on frequency-response curve

5 结论与展望

（1）基于有限元软件ANSYS Maxwell建立了健康绕组模型，计算其电容、电感参数矩阵，并通过与解析公式法计算值对比，验证仿真建模与计算的正确性；

（2）建立了绕组不同变形类别和变形程度的模型，仿真得到等值电路模型的电容和电感参数，并在此基础上模拟绕组变形现象，得到绕组变形影响等值电路参数变化的规律；

（3）利用电路仿真软件PSPICE得到绕组变形下的频率响应特性曲线，揭示了绕组变形导致频率响应曲线变化的规律，并通过仿真发现，不同变形类别和变形程度绕组的频率响应特性曲线体现出规律性，频率响应特性曲线谐振点变化能综合反映绕组变形信息；

（4）仿真思路能为频率响应图谱的解释提供一定的参考依据，后续可提取反映频率响应特性的特征参量，并结合神经网络等智能算法实现绕组变形类别的识别，还可搭建模型变压器试验平台对有限元仿真的思路进行验证。

［1］周求宽，万军彪，王丰华，等.电力变压器振动在线监测系统的开发与应用［J］.电力自动化设备，2014，34（3）：162-166.ZHOU Qiukuan，WAN Junbiao，WANG Fenghua，etal.Design and implementation of online vibration monitoring system for powertransformer［J］.Electric Power Automation Equipment，2014，34（3）：162-166.

［2］BAGHERI M，NADERI M S，BLACKBURN T，et al.Frequency response analysis and short-circuit impedance measurement in detection of winding deformation within power transformers［J］.IEEE Electrical Insulation Magazine，2013，29（3）：33-40.

［3］王明林，陈民铀，赖伟，等.一种改进的配电变压器短路电抗在线检测方法［J］.电力自动化设备，2015，35（3）：127-132.WANG Minglin，CHEN Minyou，LAI Wei，et al.Improved method ofonline measuring fordistribution transformershortcircuit reactance［J］.Electric Power Automation Equipment，2015，35（3）：127-132.

［4］DICK E P，ERVEN C C.Transformerdiagnostictestingby frequency response analysis［J］.IEEE Transactions on Power Apparatus and Systems，1978，97（6）：2144-2153.

［5］姚陈果，赵仲勇，李成祥，等.基于暂态过电压特性的电力变压器绕组变形故障在线检测［J］.高电压技术，2015，41（3）：873-880.YAO Chenguo，ZHAO Zhongyong，LI Chengxiang，et al.Online detecting winding deformation of power transformer based on transient overvoltage［J］.High Voltage Engineering，2015，41（3）：873-880.

［6］BAGHERI M，NADERI M S，BLACKBURN T.Advanced transformer winding deformation diagnosis：moving from off-line to online［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2012，19（6）：1860-1870.

［7］韩爱芝，刘莘昱，曾定文，等.判断变压器绕组变形的简单方法［J］.变压器，2003，40（4）：8-12.HAN Aizhi，LIU Shenyu，ZENG Dingwen，et al.Simple method to judge deformation of transformer windings［J］.Transformer，2003，40（4）：8-12.

［8］王钰，李彦明，张成良.变压器绕组变形检测的LVI法和FRA法的比较研究［J］.高电压技术，1997，23（l）：13-15.WANG Yu，LI Yanming，ZHANG Chengliang.The comparisonal study on LVI and FRA method of detecting winding deformation faults in transformers［J］.High Voltage Engineering，1997，23（1）：13-15.

［9］何平，文习山.变压器绕组变形的频率响应分析法综述［J］.高电压技术，2006，32（5）：37-41.HE Ping，WEN Xishan.Survey of frequency response analysis on winding deformation of transformers［J］.High Voltage Engineering，2006，32（5）：37-41.

［10］JENSEN J B，JENSEN B B，MIKKELSEN S D，et al.Parametric identification in potential transformer modeling［J］.IEEE Transactions on Power Delivery，1992，7（1）：70-76.

［11］ISLAM S M.Detection of shorted turns and winding movements in large power transformers using frequency response analysis［C］∥IEEE Engineering Society WinterMeeting.Singapore：IEEE，2000：2233-2238.

［12］VAESSEN P T，HANIQUE E.A new frequencyresponse analysis method for power transformers［J］.IEEE Transactions on Power Delivery，1992，7（1）：384-391.

［13］MOREAU O，GUILLOT Y，BARRE B.FRA diagnosis method：simulation applied to feasibility study and efficiency improvement［C］∥Power Engineering Society 1999 Winter Meeting.［S.l.］：IEEE，1999：1059-1064.

［14］MCDOWELLL G W，LOCKWOOD M L.Real time monitoring of movementoftransformerwinding［C］∥IEE Colloquium on Condition Monitoring and Remanent Life Assessment in Power Transformers.［S.l.］：IET，1994，3：6/1-6/6.

［15］YAO Chenguo，ZHAO Zhongyong，CHEN Yu，et al.Transformer winding deformation diagnostic system using online high frequency signalinjection by capacitive coupling ［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2014，21（4）：1486-1492.

［16］WANG M，VANDERMAAR A J，SRIVASTAVA K D.Improved detection of power transformer winding movement by extending the FRA high frequency range［J］.IEEE Transactions on Power Delivery，2005，20（3）：1930-1938.

［17］LUDWIKOWSKI K，SIODLA K，ZIOMEK W.Investigation of transformer model winding deformation using sweep frequency response analysis［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2012，19（6）：1957-1961.

［18］孟晨.多绕组电力变压器波过程的计算和分析［D］.沈阳：沈阳工业大学，2013.MENG Chen.Wave process calculation and analysis of power transformer multi winding［D］.Shenyang：Shenyang University of Technology，2013.

［19］弓杰伟，马宏忠，姜宁，等.电力变压器的有限元建模与绕组松动分析［J］.电力自动化设备，2016，36（4）：78-84.GONG Jiewei，MA Hongzhong，JIANG Ning，et al.Finite element modeling and winding looseness analysis for power transformer［J］.Electric Power Automation Equipment，2016，36（4）：78-84.

［20］中华人民共和国国家发展和改革委员会.电力变压器绕组变形的频率响应分析法：DL/T 911—2004［S］.北京：中国标准出版社，2004.