UPFC有功控制引起的交互影响研究

马 朋 ，刘 青 ，邹家平 ，刘 诚

（1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.广东国华粤电台山发电有限公司，广东 台山 529228；3.中国神华能源股份有限公司国华惠州热电分公司，广东 惠州 516082）

0 引言

统一潮流控制器UPFC（Unified Power Flow Controller）作为柔性交流输电系统FACTS（Flexible AC Transmission Systems）的第3代控制器，同时具备静态同步补偿器和静态同步串联补偿器的特点，具有独立控制有功功率、无功功率以及电压的功能［1］，被认为是最具创造性且功能最强大的FACTS元件，因而受到了产业界和学术界的普遍重视。

由于UPFC内部各控制器一般基于各自的控制目标单独制定控制策略，故可能导致UPFC的多个控制通道间产生负的交互影响，这种交互作用会影响到控制器的工作性能，甚至破坏电力系统的稳定性［2-5］。 相关的研究［6-7］表明，UPFC 的多个控制器之间存在负交互影响，系统有闭环失稳的可能性。许多学者针对交互影响存在的原因亦做了大量研究［8-10］，发现在稳态时通过UPFC内部的有功功率（即流过直流电容支路的功率）的大小和方向，是影响UPFC各控制功能之间交互影响强弱的重要因素。

然而，UPFC内部各控制器间的交互影响程度与串、并联侧变流器间所交换有功功率的联系仍有待进一步研究。本文根据UPFC的工作原理，定性分析了UPFC有功参考值的变化对电压控制器所控电压的影响，阐述了利用公式表达有功参考值变化与电压之间影响的几种途径，利用时域仿真方法采集动态电压数据，用Logistic模型对其进行拟合，得出有功补偿度变化量对节点电压变动值影响的数学表达式。该数学表达式有利于分析UPFC有功潮流控制对并联侧电压控制器运行带来的影响。

1 UPFC基本工作原理

UPFC相当于一个自给式电压源，具有交换无功功率和有功功率的能力，其补偿电压的幅值和相位角与线路电流和传输角无关。故采用UPFC能得到的最大输送功率和受端无功功率与传输角无关，其能直接控制串联变流器所安装的输电线上的潮流。UPFC基于电压源的等效电路如图1所示，串联部分等效为电压源Use和电抗Xse，并联部分等效为电压源Ush和电抗Xsh，母线k为附加节点，Zij为输电线路ij间阻抗，Ui、Uj分别为输电线路 ij首、末端电压。

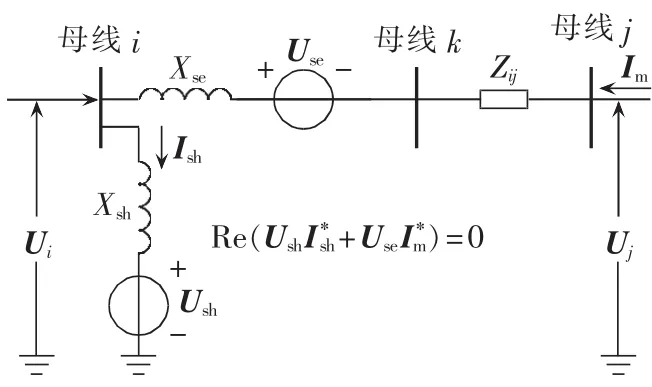
图1 UPFC基于电压源的等效电路Fig.1 Equivalent circuit of UPFC based on voltage source

以j端电压为参考电压且忽略输出线路的有功功耗，即：

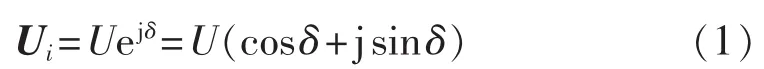
其中，U、δ分别为以j端电压为参考时，i端电压Ui的幅值和相角。

串联侧变流器与系统交换的有功、无功功率（忽略电阻）为：

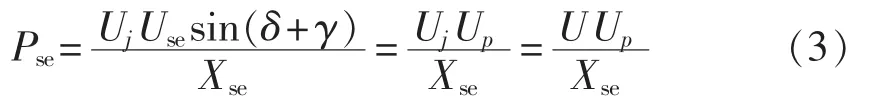
其中，γ 为 Use与 Ui的夹角；Up、Uq分别为有功、无功补偿电压。

并联侧变流器与系统交换的功率（忽略电阻）为：

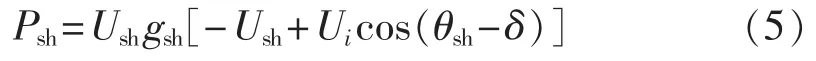
其中，gsh、bsh分别为并联侧变流器的等效电导、等效电纳；θsh为以Ui为参考时Ush的相角。

同样忽略并联侧变流器连接到系统的电阻，并联侧变流器看作STATCOM时吸收的无功功率为：

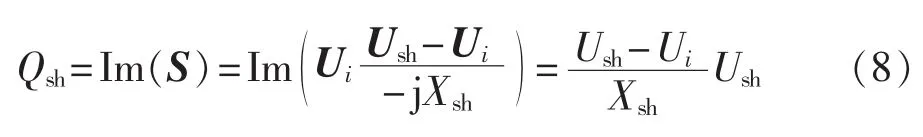
2 UPFC参考值的取值对系统电气量的影响

通过对UPFC各控制器参考值的设定和改变，潮流控制器和电压控制器能够调节UPFC安装点的电压水平和潮流分布，进而改变电力系统的运行工况［11］。设并联侧变流器补偿电压Ush的参考值为Uiref；串联侧变流器补偿有功功率Pse的参考值为Pref，补偿无功功率Qse的参考值为Qref。下面分析根据系统运行需要，UPFC补偿功率的参考值变化时对系统电气量的影响。

2.1 有功补偿参考值Pref改变

保持 Uiref、Qref的初始值不变，Pref取值调整为P′ref=Pref+ΔPref时，式（5）中Psh改变，Ush保持为Uiref不变，故当且仅当Pref的设定值发生变化时，式（7）中的相位角θsh、δ会发生相应的变化。δ=60°时有功调整的系统相量示意图如图2所示。由图2可知，θsh、δ变化会引起Qsh发生变化，即Qsh不再为0，节点电压Ui的值会发生相应变动。

图2 δ=60°时有功潮流控制的系统相量示意图Fig.2 Phasor diagram of active power-flow control with δ=60°

2.2 无功补偿参考值Qref变化

保持 Uiref、Pref的初始值不变，Qref取值调整为Q′ref=Qref+ΔQref时，仅 Uq会发生变化，不会对并联侧变流器补偿的无功Qsh产生影响，δ=60°时无功调整的系统相量示意图如图3所示。由图3可知，当Qref的设定值发生变化时，不会对电压控制器所控电压Ui的值产生影响。

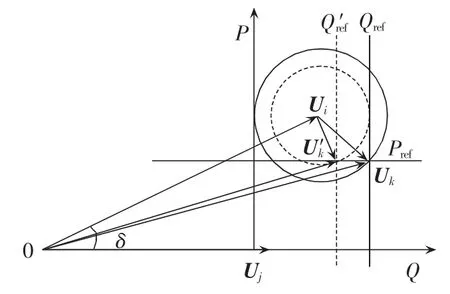
图3 δ=60°时无功潮流控制系统相量示意图Fig.3 Phasor diagram of reactive power-flow control with δ=60°

由以上分析知：

a.潮流控制器的有功补偿值Pref变化时，电压控制器所控节点电压Ui的值会发生变化；

b.潮流控制器的无功补偿值Qref变化时，电压控制器仍可稳定运行，Qref的改变不会对节点电压Ui的值产生影响。

2.3 有功调节与电压交互影响的数学表达研究

以UPFC的阻抗模型［12］为基础，对 UPFC所在输电线路的两节点网络进行分析，由于输电线路每千米的电纳一般为10-6数量级，故为简化计算，可忽略输电线路的对地电纳，对电力线路电压进行计算，得：

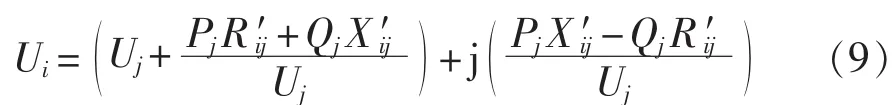
输电线路损耗方程为：

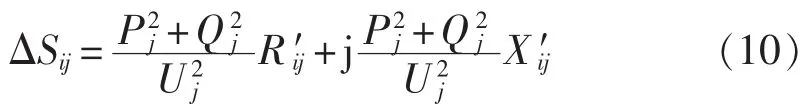
其中，Z′ij=R′ij+jX′ij= （Rij+Rp） +j（Xij+Xp），Rij、Xij分别为输电线路电阻和电抗，Rp、Xp分别为UPFC等效电阻和电抗；Pi、Qi分别为i节点注入有功、无功功率；Pj、Qj分别为j节点注入有功、无功功率。

此时，存在 Ui、Uj、ΔSij3 个未知数，但只能列写2个方程，当Zp改变后，Ui、Uj受外部电网的制约，无法求出节点电压变化与线路阻抗变化量的具体表达式。

将UPFC放入电网中考虑，以潮流计算的方法进行分析。

UPFC的控制作用可表示为Ui=Uiref，Pij+jQij=Pref+jQref，对 i节点的注入功率进行计算［13-14］，得：

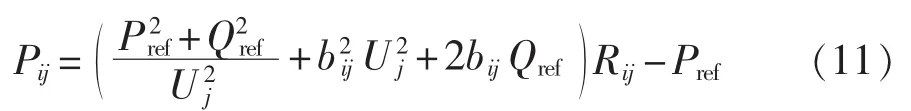
其中，Iq为以Ui为参考，Ise垂直分量的幅值。

系统节点数为n，包含r个PV节点，则传统的潮流计算要求解的方程需包含n-1个有功方程和n-r-1个无功方程，即：

由于UPFC对节点电压的控制作用，i节点在计算时从PQ节点转化为PV节点，无功方程则用电压差方程代替，即：

UPFC调节潮流的作用，可采用节点功率等值的方法，将UPFC连同所在支路去掉，在支路的两端以注入附加功率的形式放进功率平衡方程中，即：

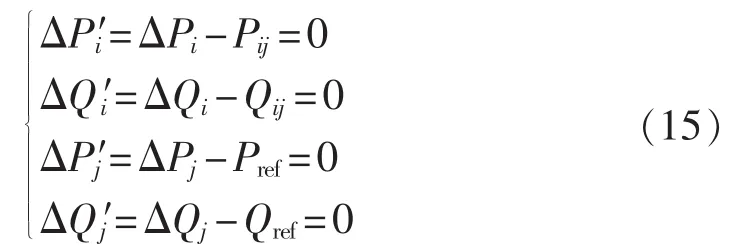
对模型求解时，UPFC所在支路被当作断开，故雅可比矩阵中的对应项需修正。

由式（11）得，i节点有功功率注入量对应雅可比式子的增量为：

对Nij、Mij、Lij进行修正后的雅可比项分别为：

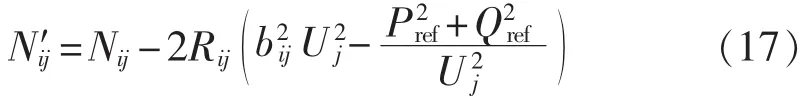
有功参考值改变，即改变潮流计算的雅可比矩阵，可计算出节点电压的变化，但一般的潮流计算是数值解法，无法进行参数运算。因此解析出节点电压变化的具体表达式很困难。

若是想得出UPFC有功补偿与节点电压间的交互影响，必然要假定一个已知的系统，对不同补偿度情况进行数据采集，从采集的数据来分析或是拟合它们的交互影响关系。

3 补偿度设定及仿真分析

本文以图4所示IEEE的标准3机9节点系统［14］为例，在PSCAD/EMTDC中进行仿真，UPFC装置安装在母线节点7、8之间，UPFC的并联侧电压控制器采用电压控制模式，串联侧潮流控制器采用直接电压调节模式。

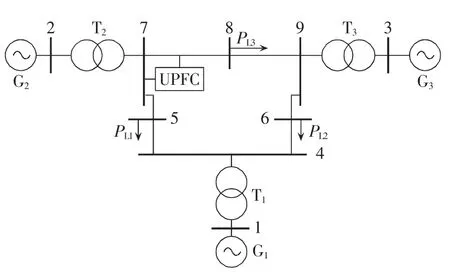
图4 IEEE 3机9节点系统图Fig.4 IEEE 3-machine 9-bus system

规定串联侧变流器补偿的有功功率流向UPFC所在线路为正，假设5 s时潮流控制器根据系统需要调整有功补偿参考值，来稳定输电线路有功潮流。

3.1 有功补偿度的设定

FACTS装置通常根据各自的功能来定义补偿度［15-18］，其中UPFC是具有多种功能的FACTS元件，UPFC的补偿度需根据不同的控制目标进行定义。定义UPFC进行有功潮流调节时的补偿度λ=Up/UN（UN为系统标称电压），来体现UPFC向系统补偿有功功率的大小。

3.2 有功补偿度改变产生的交互影响

定义有功调节补偿度变化量Δλ=ΔUp/UN，来体现UPFC串、并联侧换流器间交换的有功功率（即对UPFC所在线路调整的有功潮流）的变化。

3.2.1 UPFC补偿度λ未变化

UPFC装置补偿度未变化（即补偿度变化量Δλ为0）时，UPFC工作情况如图5所示，并联侧控制器稳定运行，UPFC接入点电压维持稳定。图中，U7为 UPFC接入点节点7的母线电压；Udc为UPFC串、并联侧间直流电容电压。

图5 补偿度不变时UPFC的工作情况Fig.5 Operating conditions of UPFC with constant compensation degree

3.2.2 负向动态有功补偿

根据系统需要，UPFC装置向所在线路补偿负的有功功率，不同补偿度变化量对应电压控制器所控电压U7波动情况如图6所示（U7为标幺值）。由图6可知，UPFC接入点电压会发生波动，且补偿度变化量不同时，UPFC接入点节点电压波动情况亦不同，严重时会使并联侧闭环系统失去稳定。

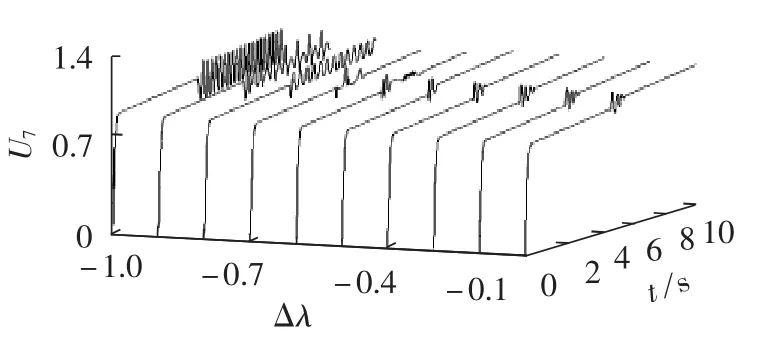
图6 负向补偿时电压波动情况Fig.6 Voltage fluctuation during negative compensation

3.2.3 正向动态有功补偿

根据系统需要，UPFC装置向所在线路补偿正的有功功率调整线路潮流，UPFC接入点电压U7波动情况如图7所示（U7为标幺值）。由图7可知，当有功补偿度变化量不同时，UPFC接入点节点电压波动情况也不同，严重时会造成并联侧闭环系统失去稳定。

图7 正向补偿时电压波动情况Fig.7 Voltage fluctuation during positive compensation

4 交互影响指标选取及Logistic模型拟合分析

4.1 交互影响指标的选取

电压波动是由一系列电压（方均根值）变动引起的。根据电能质量国家标准［19］，电压波动的合格判据以电压变动限值为衡量标准，不同电压等级对应不同的电压变动限值，对于35 kV＜UN≤220 kV的高压系统，电压变动限值为2.5%。本文将电压变动值作为有功潮流控制器与电压控制器运行间的交互影响指标。

时域仿真能展示出动态的电压数据，这是潮流计算无法比拟的优势。利用PSCAD仿真不同有功补偿度变化量对应的电压变动值，时域仿真所得交互影响指标d的部分数据如表1、表2中dk所示。其中，k代表采样数据的组号，Δλk为有功补偿度变化量，dk为UPFC接入点电压U7的变动值（交互影响指标），yk为采样数据dk的2条渐近线转化为0和1后的对应值，ωk为对数据yk求取的权数。

UPFC装置进行负向有功补偿，随着补偿度变化量Δλ值的增大，节点7的电压变动值开始稳定一段，然后经历随Δλ的增大而增大的阶段，最后逐渐趋于一个稳定值。

UPFC装置对所在输电线路进行正向有功补偿，随着补偿度变化量Δλ的增加，节点7的电压变动值开始稳定一段，然后随着Δλ的增加而减小，最后逐渐趋于一个稳定值。

围绕本节课重难点，我选择今年时政热点“韩国乐天事件”进行一例贯穿探究，采用“平台在线讨论”和“小组合作探究”两种形式分别突破，达成知识目标。

4.2 分组数据的Logistic模型

采用分组数据的Logistic回归模型［20-21］，对UPFC有功补偿采样数据进行拟合，设组号为k，自变量为Δλk，因变量为 dk（表示在自变量 Δλk的条件下，原0-1型随机变量等于1的比例）。

为了更好地求取回归模型，将UPFC进行负向有功补偿时所得采样散点图的2条渐近线转化为0和1，即因变量dk化为yk。假设每组样本数为100（即nk=100，其中 k=1，2，…，n）计算权数 ωk，yk、ωk的计算结果如表1所示。建立SPSS的数据集，借助SPSS软件求取用加权最小二乘法得到的Logistic回归方程。

表1 UPFC负向补偿时的采样数据Table1 Sampled data during negative compensation of UPFC

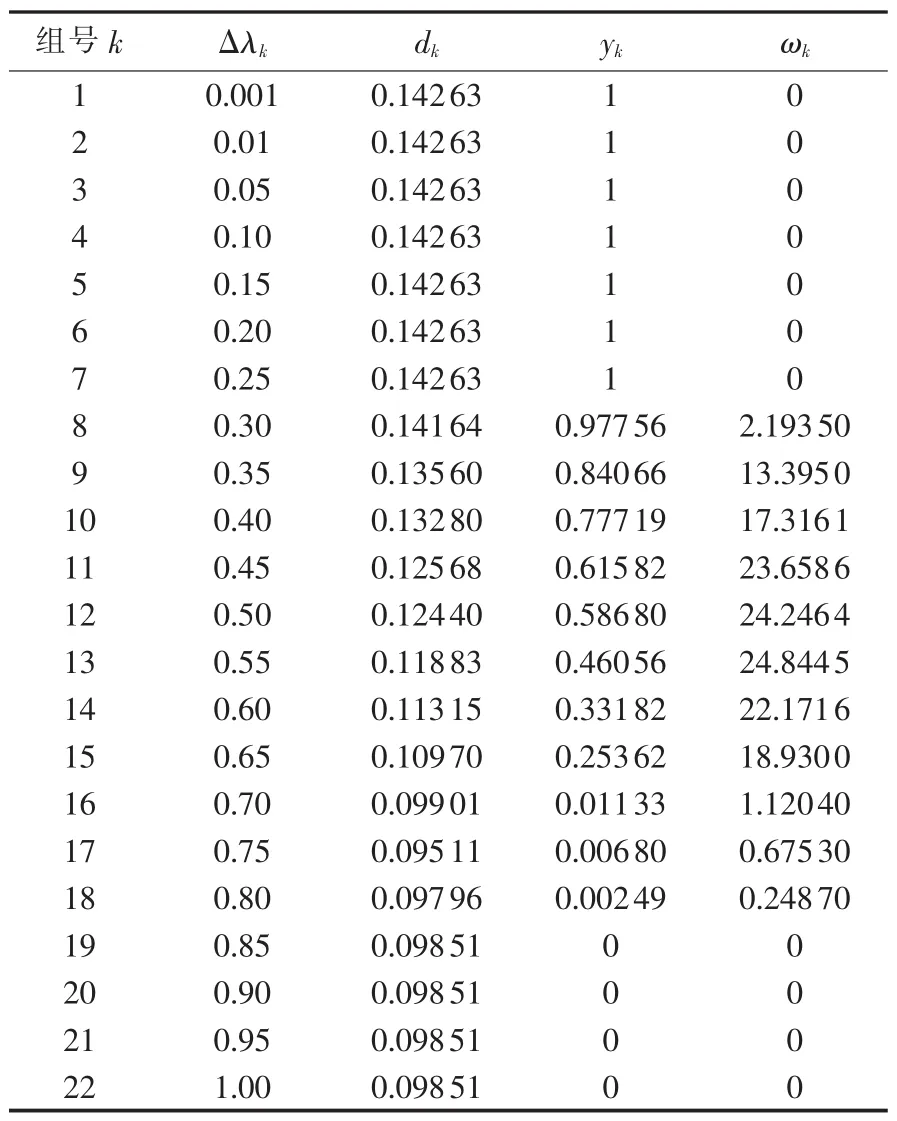
表2 UPFC正向补偿时的采样数据Table2 Sampled data during positive compensation of UPFC

负向有功补偿时，建立的Logistic回归模型为：

将式（20）还原为因变量为dk的Logistic回归方程，可得：

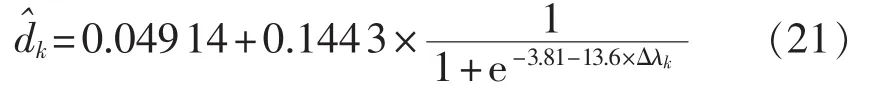
UPFC向所在线路进行不同程度负向有功补偿所得采样散点图及Logistic回归模型如图8所示。

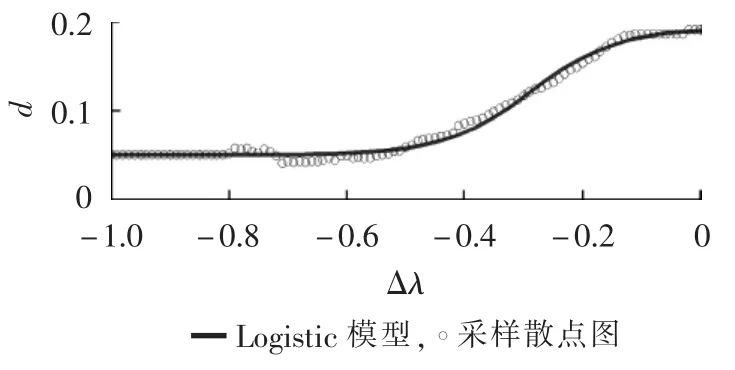
图8 Logistic模型拟合负向补偿散点图Fig.8 Scatter diagram of negative compensation for Logistic model fitting

同理，利用表2中正向有功补偿所得数据进行Logit变换及应用加权最小二乘法，可得因变量为yk的Logistic回归模型为：

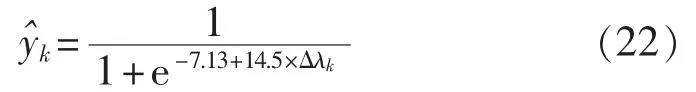
将式（22）还原为因变量为dk的Logistic回归方程，可得：

UPFC向所在线路进行不同程度正向有功补偿所得采样散点图及Logistic回归模型如图9所示。

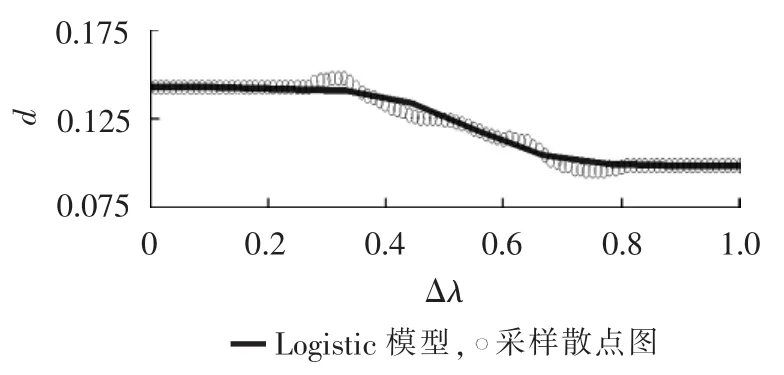
图9 Logistic模型拟合正向补偿散点图Fig.9 Scatter diagram of positive compensation for Logistic model fitting

4.3 Logistic模型的拟合有效性验证

回归方程对样本观测值的拟合程度需用样本决定系数R2=1-SSE/SST来判断，UPFC进行有功补偿时的实际采样值与拟合得到的Logistic回归模型预测值对比如表3所示。

残差平方和为：

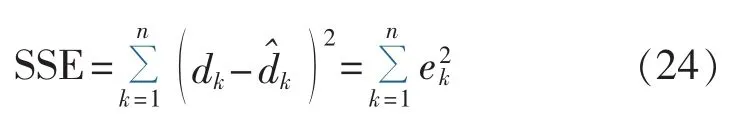
回归平方和为：

表3 实际采样值dk与回归预测值对比表Table3 Comparison between sampled dkand predicted

表3 实际采样值dk与回归预测值对比表Table3 Comparison between sampled dkand predicted

组号k负向有功补偿 正向有功补偿Δλk dk dˆk Δλk dk dˆk 1 -0.001 0.19157 0.190271 0.001 0.14263 0.142594 2 -0.01 0.19157 0.189869 0.01 0.14263 0.142589 3 -0.05 0.18693 0.187396 0.05 0.14263 0.142557 4 -0.10 0.18693 0.181977 0.10 0.14263 0.142480 5 -0.15 0.17672 0.172438 0.15 0.14263 0.142321 6 -0.20 0.15305 0.157131 0.20 0.14263 0.141997 7 -0.25 0.13141 0.135877 0.25 0.14263 0.141343 8 -0.30 0.11633 0.111608 0.30 0.14164 0.140053 9 -0.35 0.09880 0.089383 0.35 0.13560 0.137620 10 -0.40 0.08500 0.072781 0.40 0.13280 0.133402 11 -0.45 0.07716 0.062170 0.45 0.12568 0.127047 12 -0.50 0.05840 0.056049 0.50 0.12440 0.119248 13 -0.55 0.05124 0.052725 0.55 0.11883 0.111767 14 -0.60 0.05125 0.050979 0.60 0.11315 0.106108 15 -0.65 0.04983 0.050077 0.65 0.10970 0.102549 16 -0.70 0.04930 0.049616 0.70 0.09901 0.100563 17 -0.75 0.05186 0.049382 0.75 0.09511 0.099529 18 -0.80 0.05098 0.049263 0.80 0.09796 0.099009 19 -0.85 0.04914 0.049202 0.85 0.09851 0.098753 20 -0.90 0.04914 0.049171 0.90 0.09851 0.098628 21 -0.95 0.04914 0.049156 0.95 0.09851 0.098567 22 -1.00 0.04914 0.049148 1.00 0.09851 0.098538

由表3中数据得，UPFC进行负向有功补偿时，SSE=0.000586，SST=0.202017，故 R2=0.997099，R2的取值在［0，1］区间内，越接近1，表明回归拟合效果越好，这说明式（21）所示Logistic回归模型的拟合效果很好；UPFC装置进行正向有功补偿时，SSE=0.000211283，SST=0.007 962，R2=0.973 46，说明式（23）所示Logistic回归模型的拟合效果亦很好。故应用拟合后的Logistic回归模型即可预测不同补偿度变化量时电压变动值的大小，可用来分析UPFC装置有功潮流控制与电压控制间的交互影响程度。

5 结论

本文针对UPFC参考值的不同取值对系统电气量的影响进行了分析，表明UPFC调整有功潮流会引起节点电压波动。通过PSCAD/EMTDC仿真得到了不同补偿度变化量时电压的变化情况，发现不同的补偿度变化量均造成不同程度的电压波动。提出了以UPFC接入点节点电压变动值作为计量UPFC串、并联侧控制器间交互影响强弱的指标，运用Logistic模型有效拟合了交互影响曲线，完成不同补偿度变化量下交互影响程度的预测，有利于分析UPFC有功潮流控制时对并联侧电压控制器运行带来的影响。

［1］王晶，陈学允.UPFC对动态电能质量影响的分析研究［J］.电工技术学报，2004，19（1）：44-48.WANG Jing，CHEN Xueyun.Study of the impacts of UPFC on dynamic power quality［J］.Transactions of China Electrotechnical Society，2004，19（1）：44-48.

［2］曹一家，陶佳，王光增，等.FACTS控制器间交互影响及协调控制研究进展［J］.电力系统及其自动化学报，2008，20（1）：1-8.CAO Yijia，TAO Jia，WANG Guangzeng，et al.Research progress on interaction and coordinated control among FACTS controllers［J］.Proceedings of the CSU-EPSA，2008，20（1）：1-8.

［3］ZOU Z Y，JIANG Q Y，CAO Y J，et al.Normal form analysis of the interactions among multiple SVC controllers in power systems［J］.IEE Proceedings-Generation，Transmission and Distribution，2005，152（4）：469-474.

［4］祁桂刚，黎灿兵，曹一家，等.SVC和TCSC控制器间动态交互影响分析［J］.电力自动化设备，2014，34（7）：65-69.QI Guigang，LI Canbing，CAO Yijia，et al.Analysis on dynamic interaction between SVC and TCSC controllers［J］.Electric Power Automation Equipment，2014，34（7）：65-69.

［5］徐泰山，朱广飞，鲍颜红，等.广域直流阻尼控制中多模式交互影响在线分析［J］.电力自动化设备，2016，36（5）：49-54.XU Taishan，ZHU Guangfei，BAO Yanhong，et al.Online analysis of multi-mode interaction in wide-area HVDC damping control［J］.Electric Power Automation Equipment，2016，36（5）：49-54.

［6］徐榕，于泳，杨荣峰，等.H桥级联STATCOM直流侧电容电压平衡控制方法［J］.电力自动化设备，2015，35（5）：15-22.XU Rong，YU Yong，YANG Rongfeng，et al.DC capacitor voltage balance control of H-bridge cascaded STATCOM［J］.Electric Power Automation Equipment，2015，35（5）：15-22.

［7］桂帆，江道灼，吕文韬，等.限流式统一潮流控制器参数设计及优化［J］.电力自动化设备，2013，33（11）：160-164.GUI Fan，JIANG Daozhuo，LÜ Wentao，et al.Parameter design and optimization of unified power flow controller with fault current limiting［J］.Electric Power Automation Equipment，2013，33（11）：160-164.

［8］WANG H F，JAZAERI M，CAO Y J.Operating modes and control interaction analysis of unified power flow controllers［J］.IEE Proceedings-Generation，Transmission and Distribution，2005，152（2）：264-270.

［9］WANG H F，JAZAERI M,CAO Y J.Analysis of control conflict between UPFC multiple control functions and their interaction indicator［J］.Journal of Control，Automation and Systems，2005，3（2）：315-321.

［10］邹振宇.多灵活交流输电控制器间交互影响分析及其协调控制研究［D］.杭州：浙江大学，2006.ZOU Zhenyu.Research on interaction analysis and coordinated control of the multiple FACTS controllers in power system［D］.Hangzhou：Zhejiang University，2006.

［11］杜文娟，秦川，王海风，等.UPFC控制的协调设计——变参数开环解耦控制方法［J］.电力系统自动化，2008，32（8）：19-23.DU Wenjuan，QIN Chuan，WANG Haifeng，et al.Coordinated design of UPFC-a variable-parameter open-loop decoupling method［J］.Automation of Electric Power Systems，2008，32（8）：19-23.

［12］段献忠，陈金富，凌煦.潮流计算中FACTS元件模型选择研究［J］.电工技术学报，1999，14（3）：65-69.DUAN Xianzhong，CHEN Jinfu，LING Xu.Study on models of FACTS devices in power flow calculation ［J］.Transactions of China Electrotechnical Society，1999，14（3）：65-69.

［13］李虎成，於益军，李峰，等.含UPFC网络的潮流计算及稳态特性仿真分析［J］.电网与清洁能源，2013，29（4）：1-6.LI Hucheng，YU Yijun，LI Feng，et al.Power flow calculation and steady state simulation analysis of power systems with UPFCs［J］.Power System and Clean Energy，2013，29（4）：1-6.

［14］吴忠强，赵立儒，贾文静，等.计及DG与STATCOM的配电网重构优化策略［J］.电力自动化设备，2016，36（1）：111-116.WU Zhongqiang，ZHAO Liru，JIA Wenjing，et al.Optimal reconfiguration of distribution network with DG and STATCOM［J］.Electric Power Automation Equipment，2016，36（1）：111-116.

［15］万波，张焰.一种新的UPFC潮流计算模型［J］.电力自动化设备，2003，23（12）：25-27.WAN Bo，ZHANG Yan.A new UPFC model for power flow analysis［J］.Electric Power Automation Equipment，2003，23（12）：25-27.

［16］程汉湘，聂一雄.柔性交流输电系统［M］.北京：机械工业出版社，2013：187-256.

［17］罗承廉，纪勇，刘遵义.静止同步补偿器（STATCOM）的原理与实现［M］.北京：中国电力出版社，2005：1-10.

［18］徐榕，于泳，杨荣峰，等.基于无源性理论的H桥级联STATCOM非线性控制策略［J］.电力自动化设备，2015，35（1）：50-57.XU Rong，YU Yong，YANG Rongfeng，et al.Strategy based on passivity theory for online arc ontrol of STATCOM with cascaded H-bridges［J］.Electric Power Automation Equipment，2015，35（1）：50-57.

［19］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.电能质量 电压波动和闪变：GB/T 12326—2008［S］.北京：中国标准出版社，2008.

［20］吉蕴，李祖平.逻辑斯谛模型及其应用［J］.潍坊学院学报，2009，9（5）：78-80.JI Yun，LI Zuping.Logistic model and its application［J］.Journal of Weifang University，2009，9（5）：78-80.

［21］何晓群，闵素芹.实用回归分析［M］.北京：高等教育出版社，2014：217-239.