基于DVR的感应电动机柔性快速再启动方法

黄 迪，曾 正，邵伟华，胡博容，黄文涛，冉 立

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

电力系统中有很多对供电可靠性要求较高的感应电动机负荷，为了保证此类重要负荷的不间断运行，需要在电动机因故障引起跳闸后进行重合闸或者备用电源投入等“再启动”操作。感应电动机失电后电压幅值和频率衰减较慢［1］，残压的存在给再启动操作造成困难［2］。如果不采取有效策略，再启动过程会出现比静止状态下启动更大的冲击电流和冲击转矩。冲击电流可能导致保护装置误动，使电源恢复失败；冲击转矩会对电动机自身以及负载造成危害；同时由冲击造成的大量谐波成分也会导致供电质量下降，影响同一母线上设备的正常工作［3-7］。当电动机容量较大时，电源恢复引发的冲击电流对电源、电动机及负载的危害更为严重。因此，感应电动机失电后的残压以及柔性快速的再启动方法具有重要的研究价值［8-10］。

传统感应电动机的再启动采用重合闸或者备用电源投入的方式。一方面，重合闸过程通常不检测电源电压和电动机残压的相位，容易造成反相合闸，因压差过大而造成过电流并启动系统过流保护；另一方面，采用备用电源投入来实现电动机再启动的方案中，为了避免投入时刻备用电源电压和电动机残压的差值过大，通常的处理办法有低残压投入、同期捕捉投入、快速投入［10-13］。然而哪种切换方式最有利于抑制冲击问题，在什么时刻进行电源切换最有利，以往文献对此讨论较少，大多是定性分析冲击问题。同时，重合闸和备用电源投入均为机械式操作，速度受到了很大制约。值得指出的是，借助于电力电子灵活的电能变换过程和高速的开关过程，可以为感应电动机的再启动过程提供柔性和快速的解决方案。作为典型的电力电子设备，动态电压恢复器 DVR（Dynamic Voltage Restorer）是一种串联型电能质量控制装置。随着电力用户对电能质量要求的提高，各国研究者对DVR进行了广泛的研究［13-17］。在重要的感应电动机负载处加装DVR可以大幅提高其供电质量和可靠性。首先，当电网电压发生暂降时，DVR通过注入一个幅值和相位可调的串联补偿电压，以保证电动机上电压恒定；其次，当电动机侧发生短路或者其他故障引起电动机失电情况下，DVR作为一种可控电源，有能力实现感应电动机的柔性快速再启动，这正是本文研究内容的切入点。

本文针对感应电动机在残压状态下的再启动问题，提出利用DVR来生成“柔性电压”以实现感应电动机安全、快速再启动的方法。“柔性电压”是指从再启动开始到启动结束这一过程中加在感应电动机上的过渡电压，它可以最大限度地减小再启动冲击，同时能够保证启动速度。在分析了感应电动机再启动过程中由残压引起的冲击机理之后，给出了“柔性电压”的指令计算方法和DVR控制实现，利用仿真结果验证了所提方案的正确性和有效性。

1 感应电动机失电残压及对再启动的影响

感应电动机失电残压产生的机理为：定子侧电源断开后，定子电流变为零，根据电磁感应定律和楞次定律，转子回路中会产生瞬时感生电流，抵消定子电流消失引起的磁通变化。感生电流按转子绕组时间常数衰减，是缓变的直流量，其产生的磁场，相对定子绕组以转子转速旋转，在定子绕组中感生出电动势，即感应电动机的失电残压［2］。电动机失电后定子端电压（标幺值）的典型波形如图1所示。

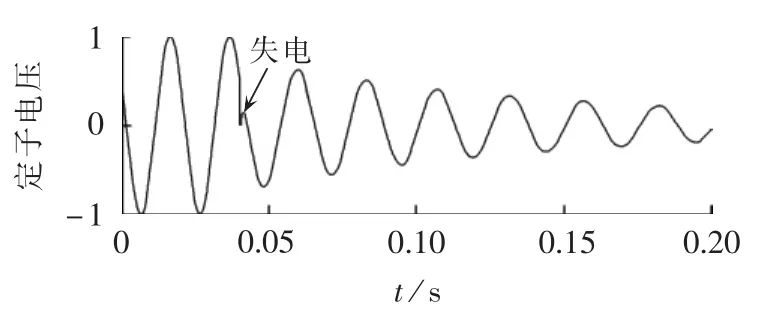
图1 感应电动机残压波形Fig.1 Waveform of induction motor residual voltage

图1中，0.04 s之前定子电压为额定工作电压，电动机正常工作；随后电动机失电，0.04～0.20 s之间的波形即为电动机的残余电压波形，可见残压的幅值和频率都是不断衰减的，而且在失电时刻电压发生突变。

感应电动机定子失电后A相电压的表达式为［2］：

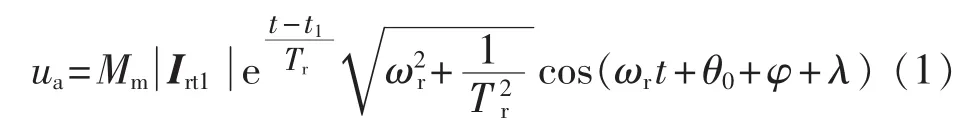
其中，Mm为电动机的互感；Irt1为电动机定子失电时刻转子电流空间向量的初始值，通过断电前后磁链不跃变可求得，为其模值，λ为相角；t1为定子失电的时刻；Tr为转子的电路时间常数；ωr为转子的电角速度；θ0为失电时刻转子轴线和定子轴线的夹角；φ =arctan（-Trωr）。

由式（1）可知，感应电动机残压的频率由转子转速决定，失电后残压频率随转速降低而减小；残压幅值由失电时刻转子电流初值、转子时间常数和转子转速共同决定，且随失电时间逐渐衰减［2］。

图2给出电动机在有残压时重新接通电源的等值电路和相量图，其中US为电源电压，XS为电源等值电抗，UD为感应电动机的残压，XD为电动机的等值电抗，ΔU为电源电压和残压之间的差拍电压，δ为两电压之间的相角差。合闸瞬间的冲击电流为I=ΔU/（XS+XD）。显然，合闸瞬间的冲击电流与电压差ΔU、电抗有关，在严重情况下ΔU可以近似达到2倍的额定电压，ΔU越大，则电源恢复时其对电动机的冲击越大。

图2 再启动过程的等值电路和相量图Fig.2 Equivalent circuit and phasor diagram during induction motor restart

此外，ΔU的大小与残压的幅值、相位都有关系，当残压和电源电压相位差较大时，两者的差值ΔU相当大。所以传统的备用电源投入法都是在寻找合适的合闸时间点，避免两者在反相时合闸，目的就是尽可能减小ΔU的大小。

2 残压状态下电动机快速再启动方案

由前述分析可知，要想最大限度减小电动机再启动冲击，需要使再启动初期施加电压和残压的差拍电压ΔU尽可能小，然后逐渐增大施加电压来保证快速完成启动过程。下面将阐述利用DVR达到这一效果的具体方法。

2.1 DVR拓扑结构及数学模型

三相DVR应用于感应电动机再启动的方案如图3所示，其中三相桥式电压源型变流器和串联耦合变压器T1—T3构成了DVR的主体。实际应用中变流器直流侧通常由储能元件或者整流器提供能源，图3中用Ud1和Ud2这2个大小相等的直流电压源来表示，直流侧电势中点和变压器中性点相连可以提高系统处理不对称故障的能力。Sa、Sb和Sc为三相电源，ZS为其阻抗；L1—L3和C1—C3构成三相LC滤波器。

图3 DVR系统电路结构图Fig.3 Circuitry of DVR system

三相电压源型变流器的单相等效电路模型可简化为图4［18］，其中d为电压源型变流器的等效开关占空比，其大小受变流器的调制过程控制。逆变状态下，d为正弦交流量。通过电压控制，变流器可输出一个可控的电压UDVR。

图4 电压源型变流器单相等效电路模型Fig.4 Single-phase equivalent circuit model of VSC

全耦合变压器的原边和副边电压关系与理想变压器相同，电压比与线圈匝数比成正比。为了简化分析过程，取该变压器变比为1:1，则图3中整个系统的等效电路如图5所示。

针对图4和图5，系统的控制框图如图6所示。

图5 DVR系统等效电路模型Fig.5 Equivalent circuit model of DVR system

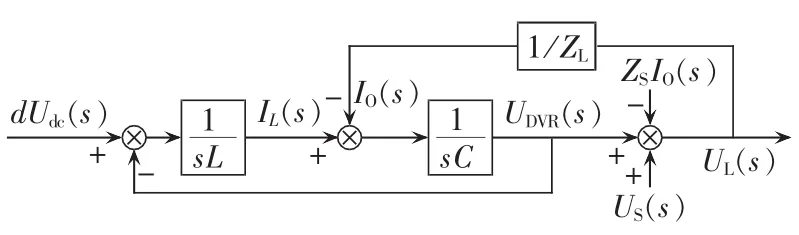
图6 系统框图Fig.6 Block diagram of system

可见，通过控制电压源型变流器的占空比d即可控制负载电压UL。

根据US+UDVR=UL，得到以负载电压为控制目标的闭环控制框图如图7所示。其中VR表示电压调节器，用于调节闭环跟踪效果。

图7 DVR闭环系统控制框图Fig.7 Block diagram of DVR closed-loop control system

2.2 快速再启动方案设计

感应电动机失电后存在残压状态下，运用DVR使其柔性快速再启动的方案示意图如图8所示（电压为标幺值，后同）。其中，虚线是电源的电压波形，A点之前的实线表示感应电动机失电后的残压波形，可见残压与电源电压存在相位差；A点之后粗实线表示经DVR补偿之后的电压波形，这一电压用于电动机的再启动。如图8所示，经DVR补偿之后的电压幅值逐渐增大，相位逐渐移动直到和电源电压相位相同。它实现了电动机残压和电源电压的无缝连接，这一过渡过程完成后，DVR退出运行，由电源正常拖动电动机运行。

图8 柔性快速再启动原理示意图Fig.8 Schematic diagram of flexible and fast restart

为了实现上述功能，需要有效检测到残压的幅值和相位信息，然后生成对应的“柔性电压”参考波形，并且通过DVR精准跟踪该参考波形。为了获得残压的相位信息，常用的方法有过零比较法、最小二乘法、软件锁相环等［19］。考虑到残压幅值在不断减小，检测幅值时可以取1个周期内的电压最大值为残压的峰值特征值。所谓峰值特征值，是把残压这一非标准正弦量在短时间内视为标准正弦时所对应的峰值。鉴于篇幅限制，本文不再详细阐述残压信息的检测，下文将重点阐释“柔性电压”参考波形的生成方法以及利用DVR准确跟踪参考电压的方法。

3 参考波形的生成方法

假设在图8中A点所对应时刻系统已经准确检测到残压和电源电压的幅值、相位信息，设残压的峰值特征值为UC，残压和电源电压的相位差为θC。再设电源电压表达式为US=A1sin（ω1t+θ1）。 设 DVR 启动和退出时刻分别是t1和t2，可知“柔性电压”工作时间为 Δt=t2-t1。

相位跟踪方法：由于残压和电源电压之间存在相位差，“柔性电压”要消除这个相位差实现两者的无缝连接就必须和电源电压的频率不相同。取“柔性电压”的角频率为 ωf，且 ωf＜ω1，令“柔性电压”的初始相位和残压相位相同，则易知经过Δt=θC/（ω1-ωf）时间之后，“柔性电压”即可达到和电源电压同相位。则“柔性电压”的表达式为：

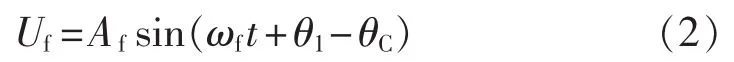
相位跟踪的原理示意图如图9所示。

图9 相位逐渐跟踪示意图Fig.9 Schematic diagram of gradual phase tracking

幅值跟踪方法：为了实现“柔性电压”幅值的逐渐增大，可取幅值 Af=UC+A2sin（ω2t+θ2），只要满足ω2Δt=π/2，且 ω2t1+θ2=0、A2=A1-UC，即可得到一个幅值Af从UC按照正弦规律逐渐增大（正弦前1/4周期）到A1的波形，如图10所示。

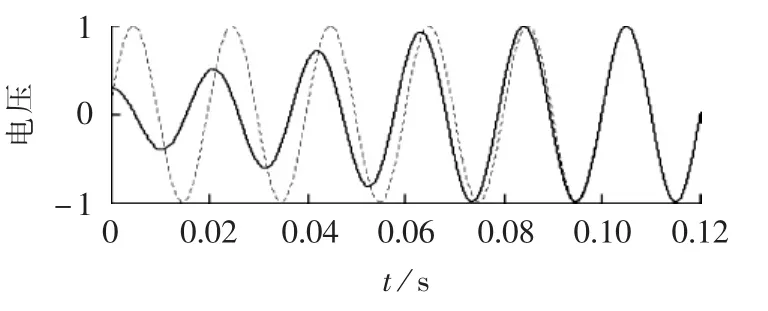
图10 幅值逐渐跟踪示意图Fig.10 Schematic diagram of gradual amplitude tracking

幅值放大的过程中，本文有意使其按照正弦规律逐渐增大而不采用线性放大。首先，正弦的前1/4周期是其单调递增区间，但是斜率是逐渐减小的，按照这种增速递减的幅值增大方式，可以避免实际跟踪过程的后期增速过大引起过冲，从而达到幅值平滑过渡的目的。其次，将“柔性电压”的幅值Af按照正弦规律递增，便于将“柔性电压”分解为几个正弦信号的叠加，为实现对其无静差跟踪提供便利。

此时，“柔性电压”的表达式变为：

可见，经过上述变换之后，得到了所需要的“柔性电压”：相位和幅值均逐渐跟踪上电源电压。而且该“柔性电压”可以分解为 3 个不同频率（ωf-ω2、ωf、ωf+ω2）的正弦信号的叠加。

经过上面的分析，各参数值的确定方法总结如下。

a.“柔性电压”启动时刻t1：取决于检测系统的速度，当检测到电动机失电以及残余电压信息后，控制系统即跳出准备状态开始工作。

b.“柔性电压”工作时间Δt：主要考虑电动机再启动过程的冲击以及快速性，Δt太小，冲击电流过大；Δt太大，启动过程慢。由于快速再启动时电动机转速下降不大，Δt取为正常启动时间的1/5以下即可。

c.“柔性电压”的角频率 ωf：ωf=ω1- θC/Δt。

d.幅值增大过程的参数：ω2=（π/2）/Δt，且θ2=- ω2t1，A2=A1-UC。

4 零误差跟踪控制方法设计

前文已经介绍了“柔性电压”指令信号的生成方法，但是由于该“柔性电压”不是标准正弦，所以给传统针对正弦或者直流信号的闭环控制方法带来挑战。下文将阐述如何设计电压调节器来实现对该“柔性电压”的零误差跟踪。

4.1 设计思路

为了达到无差跟踪指令信号的目的，闭环控制系统通常需要添加调节器。实际应用中，直流指令信号的跟踪一般需设计PI调节器，正弦指令信号一般有2种处理方法：通过可逆的变换将正弦量转化为直流量，进而用PI调节器实现跟踪；利用“广义积分器”，即比例谐振（PR）调节器，实现对正弦信号的直接跟踪。

通过上文分析可知，指令电压不是标准的正弦信号，但是可以分解为3个不同频率的正弦信号。如果对3个正弦分量分别跟踪，则自然实现了对合成信号的跟踪。这正是笔者有意使“柔性电压”指令值按照正弦规律递增的原因之一。

交流正弦指令信号可以经dq0变换转化为直流信号，因此按最终指令信号的交直流属性，可以设计出如下3种控制方案：交流下控制，使用PR调节器；交直流混合控制，使用PI和PR调节器；直流下控制，使用PI调节器。

之所以会有交直流混合控制的方案，是因为“柔性电压”指令信号是3种频率正弦信号的叠加，将其转化成纯直流信号至少需要2次dq0变换，为了简化运算，经1次dq0变换就产生了此方案，详见下文。

4.2 多谐振调节器方案

PR调节器由比例环节和谐振环节组成，其中的谐振环节又称广义积分器，可以对谐振频率的正弦量进行幅值积分，从而实现正弦信号的无静差控制［20］。

多谐振调节器由多个不同谐振频率的谐振调节器叠加而来。由于各个谐振调节器仅仅在其谐振频率点起作用，所以多个谐振调节器可以并联叠加使用［21］。

多谐振调节器的数学表达式为：

其中，Krh为第h个谐振增益；ωh为第h个谐振频率。

由于“柔性电压”中包含3种频率的正弦信号，利用三谐振调节器即可实现对其零误差跟踪，控制框图如图11所示。

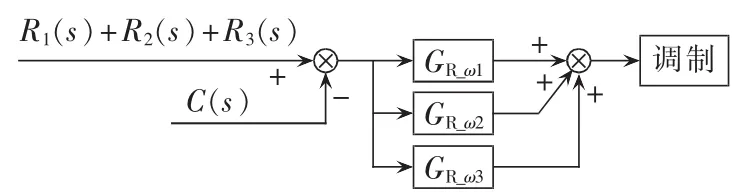
图11 三谐振调节器方案Fig.11 Scheme with three resonant regulators

图 11 中 ，GR_ω1、GR_ω2和 GR_ω3分 别 为 针 对 频 率ω1、ω2和 ω3的谐振调节器；R1（s）、R2（s）和 R3（s）分别为参考信号中的3个频率正弦分量，3个正弦分量之和即为“柔性电压”的参考信号；C（s）为实测的输出电压信号，两者作差之后经过三谐振调节器，最终输出给调制环节。

将三谐振电压调节器加入如图7所示的系统控制框图，得到系统的开环传递函数为：

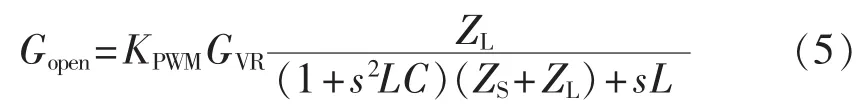
其中，KPWM为变换器的等效放大系数；GVR为图7所示电压调节器VR的传递函数。

多谐振调节器的参数设计方法主要有开环伯德图［22］、根轨迹等图解法［23］，本文不再赘述。

4.3 PI+PR调节器方案

第3节已经证明“柔性电压”是3个不同频率正弦信号的叠加，即：

写成矩阵形式为：

如果将其经过dq0变换，变换频率为ωf，变换矩阵如下：

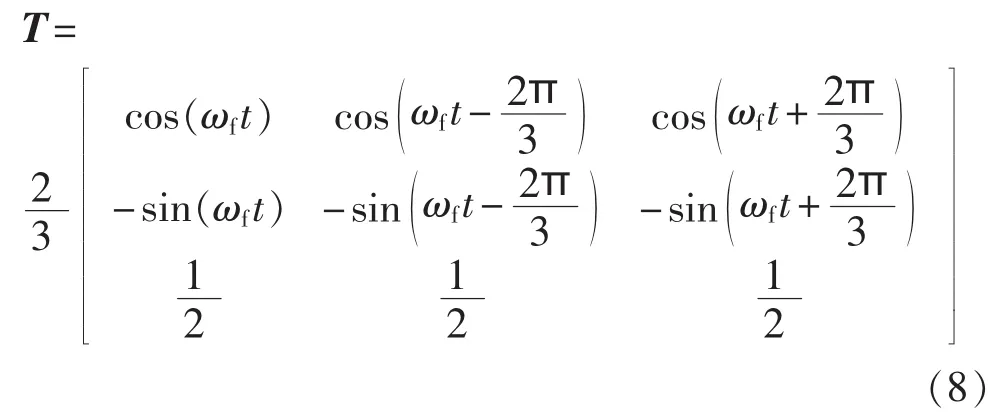
经Udq0=TUabc变换后，得到：

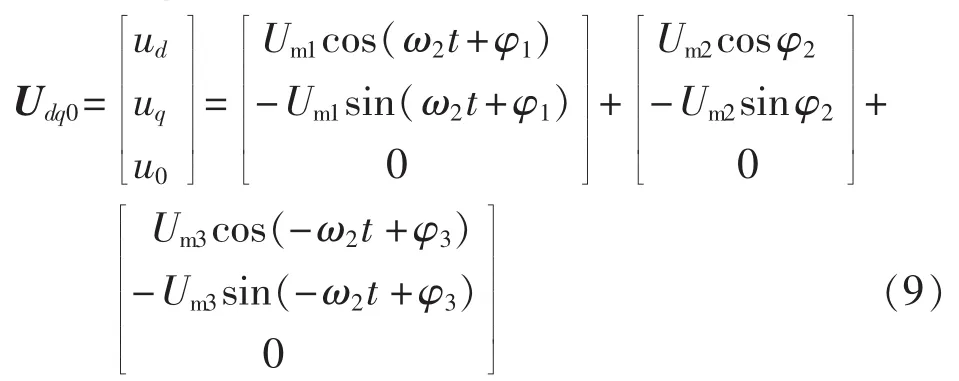
如果变换时，d轴和频率为ωf的正弦成分的电压空间矢量重合，即φ2=0，那么变换后q轴的直流分量-Um2sin φ2为 0，即变换后 d轴包含直流成分Um2cosφ2和频率为ω2的正弦成分，q轴仅包含频率为ω2的正弦成分。采用低通滤波器即可实现直流量和正弦量的分离，分离后直流成分使用PI调节器，正弦成分使用PR调节器即可实现准确跟踪。控制原理框图如图 12 所示，图中 R（s）为参考信号，C（s）为实测输出值。

4.4 PI调节器方案

在如图12所示方案的基础上，将频率为ω2的正弦成分再进行一次dq0变换，变换频率为ω2，将所有交流量变换为直流量，最后采用PI调节器即可实现零误差跟踪。原理框图如图13所示。

图12 PI+PR调节器方案Fig.12 Scheme with PI+PR regulators

图13 PI调节器方案Fig.13 Scheme with PI regulator

需要注意的是，由于经过第一次dq0变换之后的交流成分只有一相，因此在将其进行直流变换时采用的是虚拟dq0变换［24-25］，即通过计算虚拟出另外两相再进行变换。

4.5 3种方案对比

理想谐振调节器具有对输入信号频率过度敏感、易造成系统不稳定的缺点，所以通常使用准PR调节器来改进。采用准PR调节器虽然可以增大系统带宽，提高稳定性，但是由于 3个频率（ωf-ω2、ωf和ωf+ω2）相差不是很大，使得3个频率的准PR调节器相互干扰，很难设计出理想的参数。

仅利用PI调节器的方案，需要2次dq0变换运算，其中还包含1次虚拟变换，而且变换之后需要分别在d轴和q轴添加PI调节器，使控制系统变得复杂，实时性受到较大挑战。

相比上述2种方案，PI+PR调节器的方案仅采用1次dq0变换，运算比较简单；同时调节器分别设置在直流和正弦分量上，有效避免了相互干扰。综合考虑，这种方案具有设计简单、控制效果好的优点。

5 仿真结果分析

利用Simulink中的Power System仿真平台搭建DVR用于感应电动机柔性快速再启动的模型。采用鼠笼型感应电动机，额定参数为380 V/15 kW。工作于额定状态下的电动机0.2s发生失电，控制系统0.3 s启动，0.3～0.4 s期间通过“柔性电压”使得电动机完成再启动过程。采用PI+PR调节器的闭环控制方案。

图14为感应电动机定子电压以及电流（均为标幺值）的仿真结果。可见，0.3s前感应电动机处于失电残压状态，0.3s时DVR开始工作，提供给电动机的“柔性电压”与残压无缝连接。

从图14可见，感应电动机柔性再启动时，其启动电流不足额定电流的4倍；而直接再启动时，启动电流将达到额定电流的10倍左右。

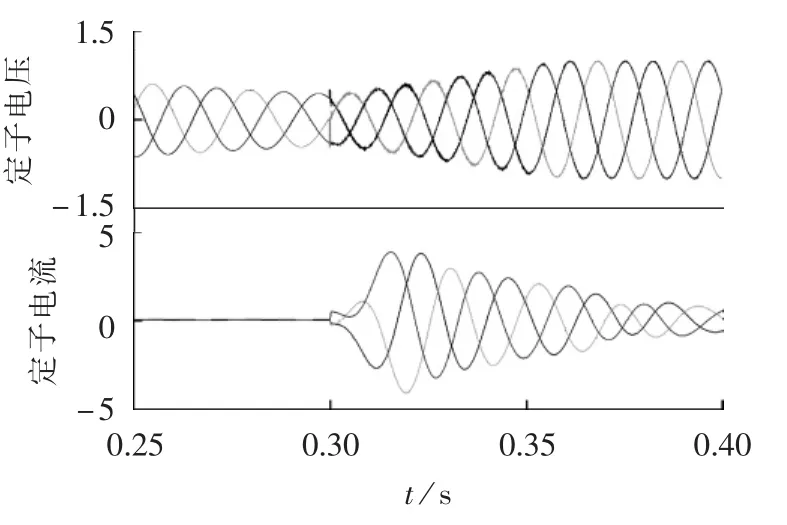
图14 定子电压和电流的仿真波形Fig.14 Simulative waveforms of stator voltage and current

观察跟踪误差，结果如图15所示，误差只有0.04 V，达到了精确跟踪的效果。

图15 误差波形Fig.15 Waveform of error

观察电动机转速以及电磁转矩（均为标幺值），如图16所示。可见，经过0.15 s即完成了再启动过程；启动转矩倍数为2，冲击很小。

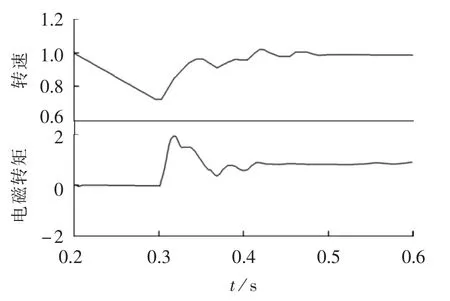
图16 转速及电磁转矩波形Fig.16 Waveforms of rotor speed and electromagnetic torque

6 结论

DVR作为一种可控电源，利用它生成的幅值和相位逐渐变化的“柔性电压”可以使感应电动机在残压状态下快速再启动。本文通过分析与对比，提出了一种简单、有效的零误差跟踪控制方法。仿真结果表明，所提出的方法可以大幅改善感应电动机的再启动过程，对保证重要电动机负荷的连续运行以及减小启动冲击有重要意义。本文提出的对“柔性电压”这种非标准正弦进行正弦分量分解从而实现对其零误差跟踪的控制方法，可以迁移到其他类似控制中，对一般非正弦交流信号的精确跟踪控制具有一定的借鉴意义。

［1］马宏忠，胡虔生，张利民，等.异步电机的失电残余电压研究［J］.中小型电动机，2005，32（5）：3-5.MA Hongzhong，HU Qiansheng，ZHANG Limin，et al.Research on residual voltage of AC motor after dump［J］.S & M Electric Machines，2005，32（5）：3-5.

［2］高吉增，杨玉磊，崔学深.感应电动机失电残压的研究及其对重合过程的影响［J］.电力系统保护与控制，2009，37（4）：45-48.GAO Jizeng，YANG Yulei，CUI Xueshen.The research of the residual voltage of induction motor after dumping and its influence during restoration［J］.Power System Protection and Control，2009，37（4）：45-48.

［3］汤蕴璆.交流电动机动态分析［M］.北京：机械工业出版社，2005：80-84.

［4］FAIZ J，GHANEEI M，KEYHANI A.Performance analysis of fast reclosing transients in induction motors［J］.IEEE Transactions on Energy Conversion，1999，14（1）：101-107.

［5］DAS J C.Effects of momentary voltage dips on the operation of induction and synchronous motors［J］.IEEE Transactions on Industry Applications，1990，26（4）：711-718.

［6］BECKWITH T R，HARTMANN W G.Motor bus transfer：considerations and methods［J］.IEEE Transactions on Industry Applications，2006，42（2）：602-611.

［7］YALLA M V V S.Design of a high-speed motor bus transfer system［J］.IEEE Transactions on Industry Applications，2010，46（2）：612-619.

［8］WANG A，LING Z，LIU W.Residual voltages analysis in reclosing process for induction machine［C］∥IEEE World Congress on Intelligent Control and Automation（WCICA）.Chongqing，China：IEEE，2008：4785-4788.

［9］汤晓燕.三相感应电动机瞬间断电重新投入电网时的瞬态［J］.电动机与控制学报，2001，5（2）：98-102.TANG Xiaoyan.Reclosing transient of three-phase induction motor［J］.Electric Machines and Control，2001，5（2）：98-102.

［10］高雅，刘卫国，骆光照.大惯量负载永磁同步电机断电-寻优重投控制系统［J］.电工技术学报，2014，29（5）：62-69.GAO Ya，LIU Weiguo，LUO Guangzhao.A large inertia load PMSM power down-rejoining on optimizing control system ［J］.Transactions of China Electrotechnical Society，2014，29（5）：62-69.

［11］邬君波.备用电源可靠自动切换研究及复杂工况分析处置［D］.杭州：浙江大学，2007.WU Junbo.Analysis and response to back power source automatic switch in complex conditions［D］.Hangzhou：Zhejiang University，2007.

［12］任果，胡军，张忠华.基于PSCAD/EMTDC的厂用大型感应电动机群聚合研究［J］.继电器，2007，35（增刊 1）：383-387.REN Guo，HU Jun，ZHANG Zhonghua.Aggregation of induction motors based on PSCAD/EMTDC in plant supply auxiliary［J］.Relay，2007，35（Supplement 1）：383-387.

［13］AKBABA M，FAKHRO S Q.New model for single-unit representation of induction motor loads，including skin effect，for power system transient stability studies［J］.IEE Proceedings B（Electric Power Applications），1992，139（6）：521-533.

［14］崔学深，张自力，李和明，等.感应电机电源切换中残压和电压差的研究及最优切换策略［J］.电工技术学报，2015，30（2）：162-171.CUI Xueshen，ZHANG Zili，LI Heming，et al.Residual voltage，voltage difference and optimal switching strategy during the power switching of induction motors［J］.Transactions of China Electrotechnical Society，2015，30（2）：162-171.

［15］WOODLEY N H，MORGAN L，SUNDARAM A.Experience with an inverter-based dynamic voltage restorer［J］.IEEE Transactions on Power Delivery，1999，14（3）：1181-1186.

［16］韩民晓，尤勇，刘昊.线电压补偿型动态电压调节器（DVR）的原理与实现［J］.中国电机工程学报，2003，23（12）：49-53.HAN Minxiao，YOU Yong，LIU Hao.Principle and realization of a Dynamic Voltage Regulator（DVR） based on line voltage compensating［J］.Proceedings of the CSEE，2003，23（12）：49-53.

［17］郭春林，刘裕昆，肖湘宁，等.三单相型DVR的分析方法和补偿策略［J］.电力自动化设备，2011，31（12）：49-53.GUO Chunlin，LIU Yukun，XIAO Xiangning，et al.Analysis method and control strategy of triple single-phase DVR ［J］.Electric Power Automation Equipment，2011，31（12）：49-53.

［18］DONG D，THACKER T，BURGOS R，et al.On zero steady-state error voltage control of single-phase PWM inverters with different load types［J］.IEEE Transactions on Power Electronics，2011，26（11）：3285-3297.

［19］周晖，齐智平.动态电压恢复器检测方法和补偿策略综述［J］.电网技术，2006，30（6）：23-29.ZHOU Hui，QI Zhiping.A survey on detection algorithm and restoring strategy of dynamic voltage restorer［J］.Power System Technology，2006，30（6）：23-29.

［20］ZMOOD D N，HOLMES D G，BODE G H.Frequency-domain analysis of three-phase linear current regulators［J］.IEEE Transactions on Industry Applications，2001，37（2）：601-610.

［21］孟建辉，石新春，付超，等.基于PR控制的光伏并网电流优化控制［J］.电力自动化设备，2014，34（2）：42-47.MENG Jianhui，SHI Xinchun，FU Chao，et al.Optimal control of photovoltaic grid-connected current based on PR control［J］.Electric Power Automation Equipment，2014，34（2）：42-47.

［22］申科，王建赜，蔡兴国，等.动态电压恢复器比例谐振控制［J］.电力自动化设备，2010，30（7）：65-69.SHEN Ke，WANG Jianze，CAI Xingguo，et al.Proportionalresonant control for dynamic voltage restorer［J］.Electric Power Automation Equipment，2010，30（7）：65-69.

［23］杨勇，赵春江.分布式发电系统中并网逆变器比例谐振控制［J］.电力自动化设备，2011，31（11）：51-55.YANG Yong，ZHAO Chunjiang.Proportional resonance controller of grid-connected inverter for distributed generation system［J］.Electric Power Automation Equipment，2011，31（11）：51-55.

［24］SILVA S M.Performance evaluation of PLL algorithms for single-phase grid-connected systems［C］∥Proceedings of IEEE Industry Applications Conference.Seattle，USA：IEEE，2004：2259-2263.

［25］ROSHAN A，BURGOS R，BAISDEN A.A d-q frame controller for a full-bridge single phase inverter used in small distributed power generation systems［C］∥Proceedings of IEEE Applied Power Electronics Conference.Anaheim，USA：IEEE，2007：641-647.