晶闸管换流阀反向恢复特性建模及阻容参数优化设计

黄 华，方太勋，刘 磊，张 翔，陈赤汉，曹冬明

（南京南瑞继保电气有限公司，江苏 南京 211102）

0 引言

近年来，我国中东部地区雾霾问题日益严重，为了缓解人口稠密地区的大气污染防治压力，同时响应国家调结构和稳增长的战略部署，国家电网在“十二五”规划中提出建设联接大型能源基地与主要负荷中心的“三纵三横一环网”特高压骨干网架和13项直流输电工程，形成西电东送、北电南送的能源配置格局。构建特高压交直流输电主网架，对于优化能源配置、保障电力供应、防治大气污染、拉动经济增长具有显著的综合经济效益和长远的战略意义［1-3］。

晶闸管换流阀是特高压直流输电的核心设备，由于晶闸管的反向恢复特性，换流阀在换相关断时将承受一个比较大的换电压过冲。晶闸管换流阀一般由几十乃至上百级晶闸管串联组成，在晶闸管两端并联阻容电路对各级晶闸管进行动态均压，并对换相电压过冲进行抑制，阻容参数的设计是否恰当关系着换流阀晶闸管能否安全可靠地长期运行。

目前很多学者采用指数函数来模拟晶闸管的反向恢复电流［4-7］，比较符合晶闸管的实际恢复过程，物理意义明确，模型参数易于获得。文献［5］给出了ABB公司采用的基于查表法的晶闸管阻尼参数设计方法，该方法虽然可以很快地计算出阻尼参数，但所查表中曲线的绘制需要进行大量的试验，试验所得的曲线不一定适用于所有的应用场合；文献［6-7］给出了采用仿真获得阻尼参数的方法，结果虽较准确，但需进行次数较多的仿真，且缺乏理论支撑；文献［8］给出了晶闸管关断过程的微分方程及反向恢复电压的时域解，但其仅给出过阻尼下的反向恢复电压时域解，未给出欠阻尼下的时域解；文献［9］给出了晶闸管阀关断电压应力的拉普拉斯解析方程，求解过程比较抽象。

本文在考虑晶闸管反向恢复过程的基础上，对晶闸管关断时刻的电路拓扑进行简化，建立相应的数学模型，求出关断时刻反向恢复电压的时域解析解，分析阻容参数对反向恢复电压峰值的影响规律，并综合考虑电压变化率和阻尼电阻损耗，得到阻容吸收参数的优化设计值；最后在PSCAD/EMTDC中搭建12脉动整流器模型，对优化设计的阻容参数进行仿真验证。

1 换流阀关断电路模型

换流阀的关断过程一般仅持续几十到几百μs，此时阀侧电压可用直流电压源来等效；以6脉动换流阀的阀V1为例，当阀V1关断时，阀V2和V3处在导通状态，且阀电抗器饱和，相当于阀V2和V3被短路，其余断态阀可用阻尼电路表示，关断阀V1用阻尼电路与反向恢复电流源并联表示；在换流阀关断过程中，阀电抗器处在未饱和状态，表现为一个线性电感；杂散电容对阀关断电压应力的影响很小［9］，可忽略。最终得到换流阀V1关断电路模型如图1所示。

图1 阀V1关断时刻拓扑电路图Fig.1 Topological circuit of valve V1at turning-off time

图1中，Lt为换流变漏感；Lrv为饱和电抗器主电感；C1为晶闸管阀等效阻尼电容，C1=Cd/Nt，Cd为晶闸管级的阻尼电容，Nt为换流阀串联晶闸管数目；R1为晶闸管阀等效阻尼电阻，R1=RdNt，Rd为晶闸管级的阻尼电阻；Id为直流电流；ir为晶闸管的反向恢复电流，其数学模型如式（1）所示。

其中，IRM为反向恢复电流峰值；τ为反向恢复电流衰减的时间常数，具体计算如式（2）所示。

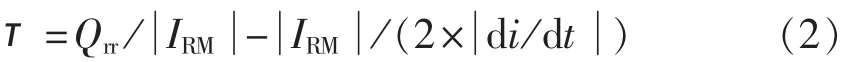
其中，Qrr为反向恢复电荷；di/dt为换相过程中的电流下降速率。

由于阀电抗器的主要作用是抑制晶闸管开通时的电流上升率，且其主电感Lrv相比换流变漏感Lt小很多，可忽略；将V1以外的电路等效变换，再接入V1，得到如图2所示的晶闸管反向恢复过程等效电路图，其中，为过电压倍数，Uv为换流器阀侧线电压。

图2 阀V1关断时刻等效电路图Fig.2 Equivalent circuit of valve V1at turning-off time

2 换流阀关断数学模型及求解

以晶闸管开始恢复阻断能力的时刻为t=0，则根据图2列出t=0时刻以后的微分方程为：

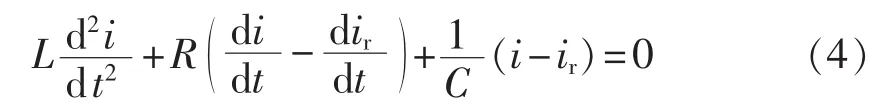
将式（4）改成标准的二次微分方程：

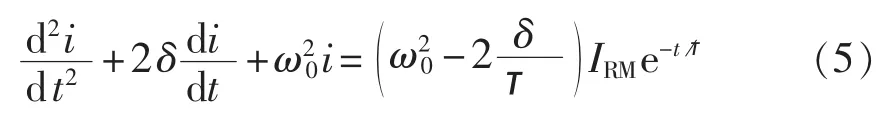
其中，

式（5）的特征根可能是：2个不等的负实根；一对实部为负的共轭复根；一对相等的负实根。以下分别对其进行求解。

2.1 2个不等的负实根

当微分方程有2个不等的负实根时，反向恢复电压非振荡衰减，根据微分方程解的形式，可设电流i的解为：

其中，为待求解系数。

初始条件为 i（0）=IRM、ut（0）=0，再结合求解微分方程常用的待定系数法，可以求得：

晶闸管的反向恢复电压ut为：

电压变化率dut/dt为：

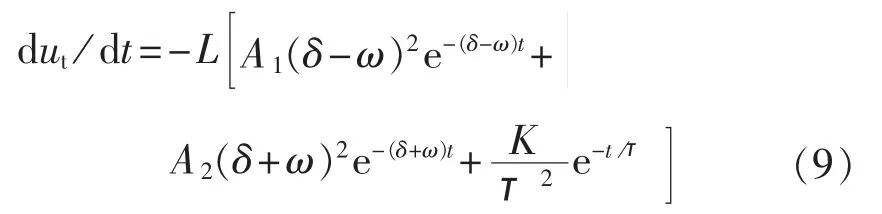
2.2 一对实部为负的共轭复根

当微分方程的根为一对实部为负的共轭复根时，反向恢复电压振荡衰减，根据微分方程解的形式，可设电流i的解为：

其中，为待求解系数。

初始条件为 i（0）=IRM、ut（0）=0，再结合求解微分方程常用的待定系数法，可以求得：

晶闸管的反向恢复电压ut为：

电压变化率dut/dt为：

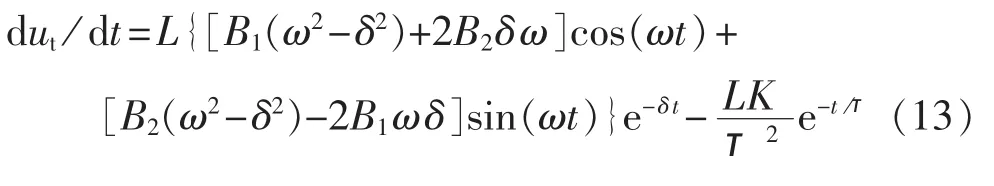
3 换流阀阻尼参数设计

当系统出现暂时过电压，晶闸管阀以触发角接近90°运行，晶闸管阀将承受最大的反向恢复电压峰值，以下所有的计算均在此工况下进行。

由式（9）和式（13）可知，晶闸管的关断电压变化率最大发生在t=0时刻，求得电压变化率最大为：

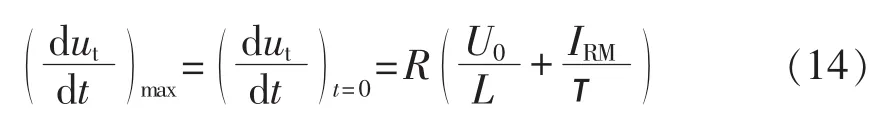
文献［10］给出了晶闸管开通时刻的阻容回路对晶闸管的放电电流及电流变化率的计算公式，根据该公式可求得电流变化率最大为：

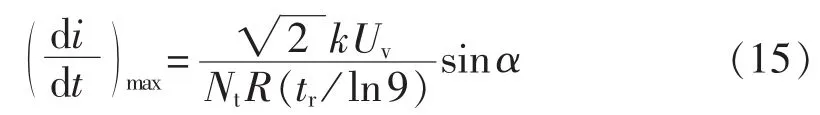
其中，tr为晶闸管开通时电流上升时间。

由式（14）、（15）可知：晶闸管关断时的电压下降率与阻尼电阻成正比，开通时刻电流上升率与阻尼电阻值成反比关系，因此阻尼电阻既不能取值太大，也不可取值太小。

由文献［11］给出的换流阀阻尼损耗的计算公式可知：换流阀阻尼损耗和阻尼电容呈线性关系，阻尼电容越大，损耗越大。

换流阀阻尼参数对换相过冲系数的影响规律为：阻尼电阻值相同时，阻尼电容值越大，换相过冲系数越小；阻尼电容值相同时，存在一个唯一的电阻值，使得换相过冲系数最小［8-9］。

因此，总结阻尼参数的设计步骤如下。

（1）根据晶闸管允许的断态临界电压上升率和开通电流上升率指标，留有一定裕度，分别由式（14）和式（15）计算出阻尼电阻的上限Rdmax和下限Rdmin。

（2）计算不考虑换相过冲时换流阀承受的关断电压U0，并根据器件的断态反向重复电压UDRM，确定最大允许的换相过冲系数βm=UDRM/U0。

（3）假定阻尼电容Cd=Cdmin（其中Cdmin为满足动态均压要求的最小阻尼电容值），根据式（8）、（10），利用MATLAB工具，绘制出阻尼电阻从Rdmin变化到Rdmax时的换相过冲曲线，观察在［Rdmin，Rdmax］区间内是否存在满足换相过冲系数小于βm的阻尼电阻值。

（4）若不存在，则增大阻尼电容值，重复进行步骤（3）；若存在，则可通过图3所示的曲线得到满足条件的临界阻尼电阻值R1、R2以及满足换相过冲最小的最优电阻Ropt。

（5）计算 min｛Ropt-R1，R1-Ropt｝是否大于 k1Ropt（其中k1为考虑电阻误差的裕度系数，可取10%），若满足，Ropt为最终阻尼电阻值，阻尼电容值即取当前Cd值，此时所得到的阻尼参数既可满足断态电压变化率、开通电流上升率的要求，又满足换相过冲和阻尼损耗最小的目标。

图3 阻尼电阻值选择示意图Fig.3 Schematic diagram of damping resistance selection

4 计算案例及仿真验证

以某一直流工程为例，Uv=178 kV，Lt=16.5 mH，Nt=60，α+μ=90°，暂时过电压系数为 1.4；查晶闸管器件手册可知，反向恢复电荷 Qrr=12000 μA·s，反向恢复电流峰值IRM=-300 A。不考虑换相过冲，晶闸管承受的反向电压峰值为U0=5873 V。

取晶闸管允许的断态临界电压上升率为3600 V/μs，开通电流上升率为 450A/μs，可得 Rdmax=162Ω，Rdmin=29 Ω；选用的晶闸管断态重复电压峰值UDRM=8500 V，计算得允许的最大换相过冲系数βm=1.45；阻尼电容从1 μF开始依次增大，绘制出从Rdmin变化到Rdmax时的换相过冲曲线，如图4所示。从图4可以看出阻尼参数对换相过冲的影响规律：阻尼电阻给定时，阻尼电容值越大，换相过冲系数β越小；对某一给定的阻尼电容值，存在唯一的阻尼电阻值，使得换相过冲系数最小。当阻尼电容增大到1.8 μF时，存在 R1=40.9 Ω、R2=53.6 Ω、Ropt=47 Ω，满足约束条件 min｛Ropt－R1，R1-Ropt｝＞k1Ropt，因此最终设计的阻尼参数为：Cd=1.8 μF，Rd=47 Ω。

图4 阻尼电阻值选择结果图Fig.4 Results of damping resistance selection

在PSCAD/EMTDC中搭建6脉动整流器仿真电路，采用带反向恢复过程的晶闸管模型，仿真系统参数与前文计算中所用参数相同，阻尼参数采用前文所得计算结果（Cd=1.8 μF，Rd=47 Ω），仿真得到在1.4倍暂态过电压和90°熄弧角时换流阀两端的电压波形如图5所示。由图可见，不考虑换相过冲的峰值电压为347 kV，考虑换相过冲的峰值电压为485.4 kV，换相过冲系数为1.39，与前文中Rd=47 Ω时的换相过冲系数1.44比较接近。

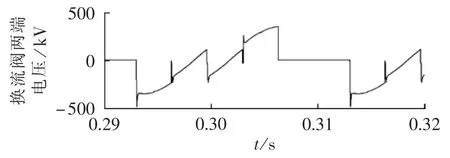
图5 换流阀两端电压波形Fig.5 Waveform of converter valve voltage

另外，取Cd=1.8μF，Rd从30Ω变化至80Ω，步长5 Ω，通过仿真得到换相过冲系数与阻尼电阻的关系曲线如图6所示。由图可见，最小换相过冲系数对应的阻尼电阻为45Ω，与前文理论计算结果47Ω接近。该仿真结果证明了阻尼参数设计方法的正确性。

图6 PSCAD/EMTDC仿真结果Fig.6 Result of PSCAD/EMTDC simulation

5 结论

本文基于晶闸管反向恢复电流的指数衰减模型，建立了换流阀关断时刻的数学模型，求解出晶闸管换流阀的反向恢复电压计算公式，总结出阻容参数对反向恢复电压过冲的影响规律，同时考虑关断时刻电压下降率、开通时刻电流上升率以及阻尼损耗等性能指标的限制，提出一种换流阀阻容参数的优化设计方法，并通过PSCAD/EMTDC仿真验证了阻容参数优化设计方法的准确性。

［1］邓旭，王东举，沈扬，等.±1100 kV特高压换流站直流操作过电压研究［J］.电力自动化设备，2014，34（1）：141-147.DENG Xu，WANG Dongju，SHEN Yang，et al.DC switching overvoltage of ±1 100 kV UHVDC converter station［J］.Electric Power Automation Equipment，2014，34（1）：141-147.

［2］邓旭，王东举，沈扬，等.±1100 kV准东—四川特高压直流输电工程主回路参数设计［J］.电力自动化设备，2014，34（4）：133-139.DENG Xu，WANG Dongju，SHEN Yang，et al.Main circuit parameter design of Zhundong-Sichuan±1100 kV UHVDC power transmission project［J］.Electric Power Automation Equipment，2014，34（4）：133-139.

［3］赵腾，张焰，叶冠豪，等.多回特高压直流分层馈入模式下交直流混联系统的稳态特性分析［J］.电力自动化设备，2016，36（8）：157-164.ZHAO Teng，ZHANG Yan，YE Guanhao，et al.Steady-state characteristics analysis for AC-DC hybrid system in hierarchicalinfeed mode of multi-loop UHVDC［J］.Electric Power Automation Equipment，2016，36（8）：157-164.

［4］申宁，杨山.基于MATLAB的晶闸管换相过电压仿真［J］.大功率变流技术，2009（2）：12-14.SHEN Ning，YANG Shan.Simulation of commutating over voltage for thyristor based on MATLAB ［J］.High Power Converter Technology，2009（2）：12-14.

［5］ABB.Design of RC snubbers for phase control applications［R］.［S.l.］：ABB，2001.

［6］中国电力科学研究院.一种新型换流阀阻尼参数设计方法：CN102136807A［P］.2011-07-27.

［7］郝勇，刘云霞，曾继伦.基于指数恢复模型的晶闸管阻容吸收参数设计［J］.电气技术，2010（2）：20-23.HAO Yong，LIU Yunxia，ZENG Jilun.A parameter design of RC snubber for thyristors based on exponential recovery model［J］.Electrical Engineering，2010（2）：20-23.

［8］解婷，汤广福，郑健超，等.高压直流晶闸管阀故障电流下反向电压特性的分析［J］.中国电机工程学报，2012，32（1）：140-146.XIE Ting，TANG Guangfu，ZHENG Jianchao，et al.Analysis on reverse voltage characteristics of HVDC thyristor valves in the fault state［J］.Proceedings of the CSEE，2012，32（1）：140-146.

［9］郭焕，温家亮，汤广福，等.高压直流输电晶闸管阀关断的电压应力分析［J］.中国电机工程学报，2010，30（12）：1-6.GUO Huan，WEN Jialiang，TANG Guangfu，et al.Analysis of the turn-off voltage stress on HVDC thyristor valve［J］.Proceedings of the CSEE，2010，30（12）：1-6.

［10］仲崇山，杨仁刚，李成榕.动态均压缓冲电路引起的晶闸管电流应力计算方法［J］.电网技术，2011，35（3）：124-128.ZHONG Chongshan，YANG Rengang，LI Chengrong.An approach to calculate current stress caused by dynamic voltage-sharing snubber circuit during thyristor turning-on process［J］.Power System Technology，2011，35（3）：124-128.

［11］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.高压直流换流站损耗的确定：GB/T 20989—2007［S］.北京：中国标准出版社，2007.