基于FLUENT的城镇燃气管道泄漏扩散模拟研究
2017-05-21罗明伟段枷亦汪双星
罗明伟,段枷亦,汪双星
(1.重庆科技学院 石油与天然气工程学院,重庆 401331;2.重庆聚祥燃气有限公司,重庆 400000)
城镇燃气管道是一个城市重要的生命线工程之一,但每年因管理不善、人为疏忽、违章操作、设备材料失效和第三方破坏等因素导致的城镇燃气管道泄漏事故时有发生,造成的物料和能量的损失、环境污染、人员伤亡和财产损失等危害给社会公共安全与和谐稳定带来极大的负面影响。因此,研究城镇燃气管道泄漏扩散,最大限度地遏制燃气事故造成的损害显得十分必要。
目前,国内外专家和学者针对气体泄漏扩散进行了一定的研究,先后提出了如高斯模型、唯象模型、Sutton模型、箱及相似模型、三维流体力学模型和浅层理论等,其特点主要表现为利用气体扩散的一般规律和实验结果数据分析拟合得出半经验半理论模型,但其计算结果的准确性很大程度上依赖于实际气体扩散条件(如泄漏类型、自然风向和强度、大气压力梯度分布、周围地形建筑等)与模型相接近的程度。本文利用FLUENT构建城镇燃气管道泄漏扩散模拟模型,研究掌握气体在一定风速和有限空间条件下的扩散规律和甲烷浓度分布规律,为有效预测城镇燃气管道泄漏扩散的影响范围提供理论依据。
1 数值模拟
1.1 问题描述
本文选择研究的城镇燃气管道管径为159×4 mm(DN150 mm),考察长度为5 km(两截断阀间距),环境温度为300K。为简化研究,选取甲烷体积分数为100%的天然气为燃气管道泄漏气体,泄漏口采用二维孔口模型,左侧水平向右风向,并取一个足够大且包含泄漏区域和扩散区域在内的空间(高50 m,泄漏半径25 m)分析气体扩散情况。模型简图如图1所示。
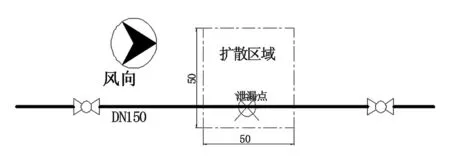
图1 模型简图
1.2 基础模型的选择
城镇燃气管道泄漏扩散的过程需遵循连续性方程、动量守恒方程、能量守恒方程和湍流控制方程。
(1)连续性方程:
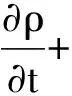
(1)
式中,ρ为流体的密度,kg/m3;t为时间,s;u为速度矢量,m/s。
(2)动量方程:
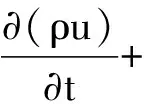
(2)
(3)能量方程:
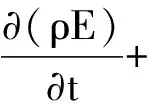
(3)
式中,E为流体微团的总能,J/kg;h为焓,J/kg,;keff为有效热传导系数,W/(m·K); Jj为组分j的扩散通量;Sh为包含了化学反应热及其他用户定义的体积热源项。
(4)湍流模型选择常用的标准k-ε模型:
(4)
(5)
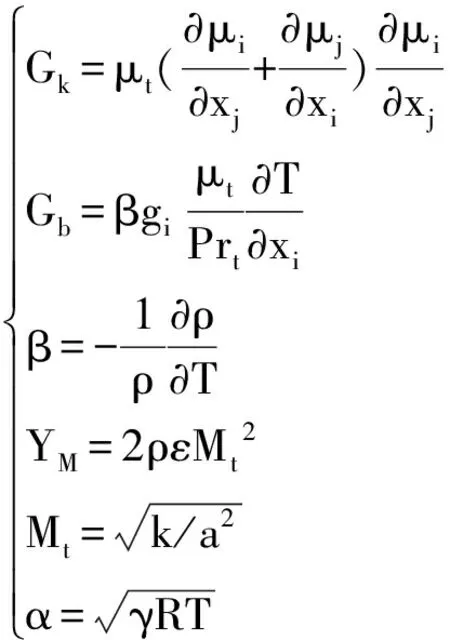
式中,Gk是由于平均速度梯度引起的湍动能;Gb是由于浮力引起的湍动能产生;YM为可压缩湍流脉动膨胀对总的耗散率的影响;C1ε、C2ε、C3ε为经验常数,FLUENT中默认值为C1ε=1.44、C2ε=1.92、C3ε=0.09;σk、σε分别为湍动能和湍动耗散率对应的普朗特数,FLUENT中默认值为σk=1.0、σε=1.3;Prt为湍动普朗特数,默认取Prt=0.85;gi为重力加速度i方向上的分量;β为热膨胀系数;Mt为湍动马赫数;a为声速。
1.3 网格模型的建立
基于FLUENT中2D计算器,考虑浮力和组分的影响,启用组分输运与化学反应模型,由于燃气管道及小孔均为对称实体,因此模拟时可简化为二维模型以减小计算量。
利用GAMBIT建立二维管道的泄漏模型,管道起点坐标(0,0),发生泄漏的区域50×50 m,忽略地形地势的影响,采用结构化网格和非结构化网格相结合的方法构建模型。由于管道泄漏口附近压力会有变化,为了提高计算的准确度,在管道泄漏口及其周围加强网格细化如图2所示。

图2 泄漏扩散网格模型
1.4 边界条件的确定
利用FLUENT确定边界条件类型,考虑风速影响时,定义泄漏口为速度入口,左侧边定义为速度进口,将计算区域最上方的3条线及右侧边定义为压力出口,如表1所示。
由此,本文在以上数值模型及求解器设定下,对两种不同泄漏孔径(0.04 m和0.06 m)和三种不同风速(0 m/s、4 m/s、6 m/s)条件下的泄漏流场进行模拟分析。
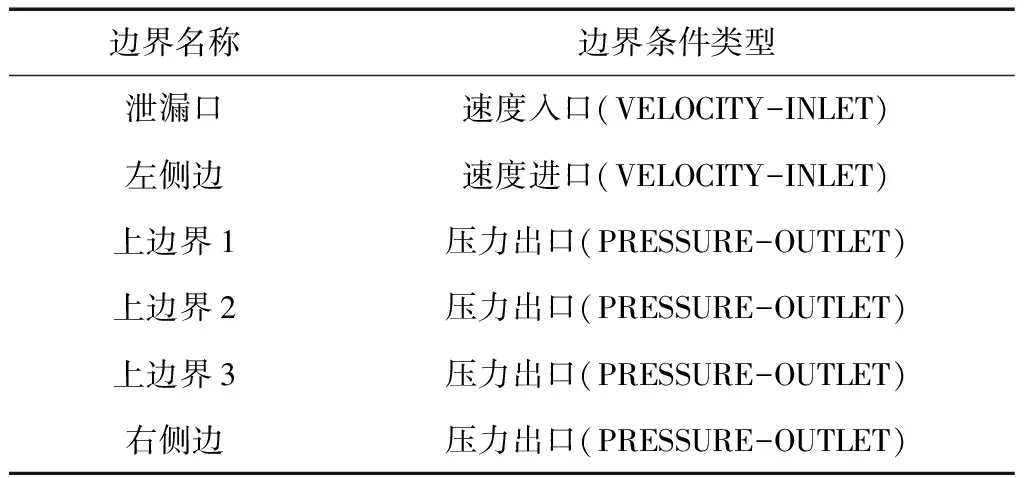
表1 边界条件表
2 计算结果分析
2.1 模拟风速与泄漏孔径对泄漏流场速度影响分析
通过FLUENT模拟计算得到不同风速条件下泄漏孔径0.04 m时泄漏流场速度分布云图如图3所示,泄漏孔径0.06m时泄漏流场速度分布云图如图4所示。
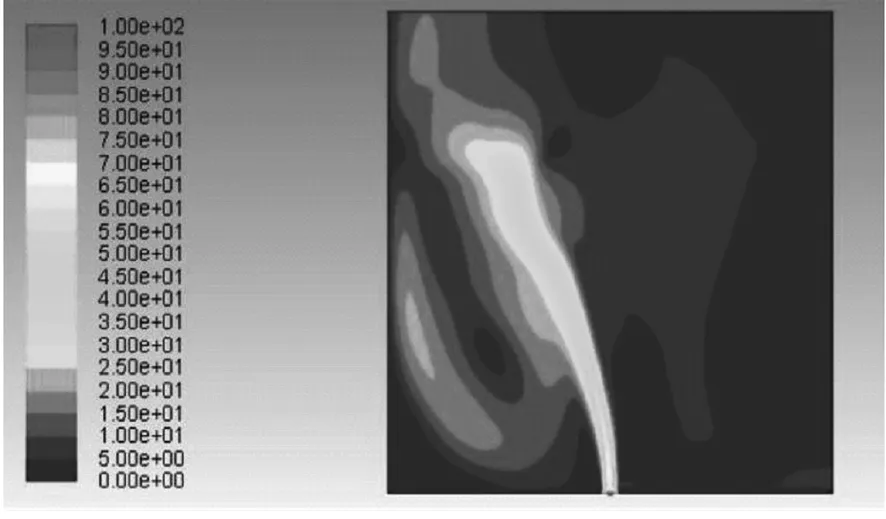
(a)风速0m/s

(b)风速4m/s
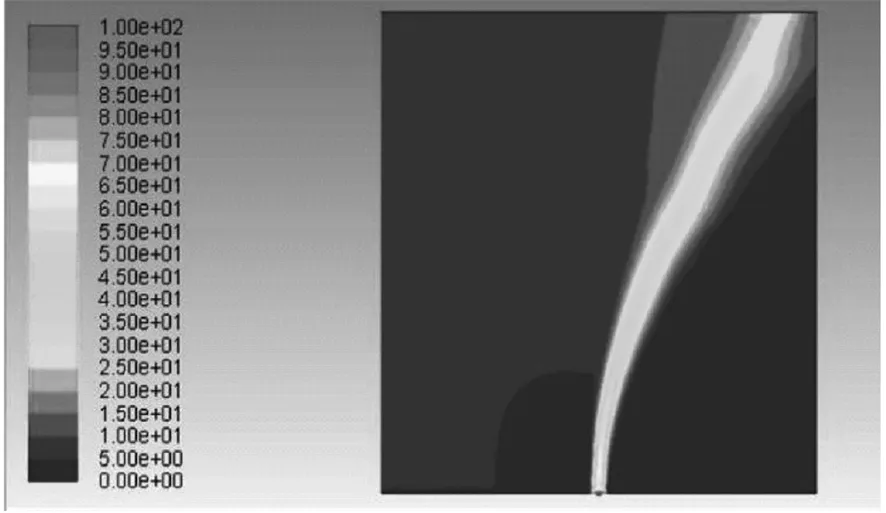
(c)风速6m/s
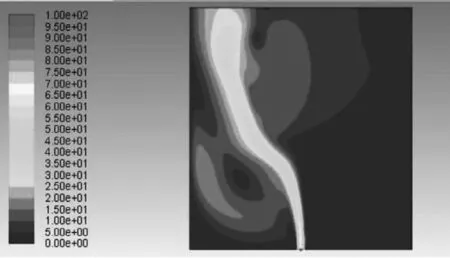
(a)风速0m/s
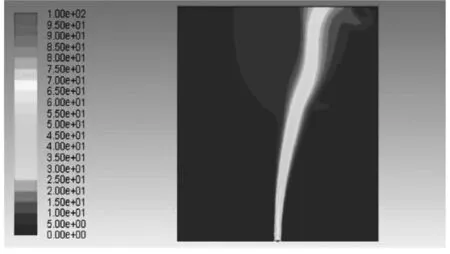
(b)风速4m/s

(c)风速6m/s
六种不同泄漏情况下的流场速度分布云图中速度最大值见表2。

表2 六种泄漏情况下的流场速度最大值
通过比较以上6种不同泄漏情况下的速度场分布云图和速度最大值情况可知:
(1)在相同泄漏孔径下,外部风速从0m/s增加到6m/s时,燃气射流最大速度逐渐变大。相同风速条件下,0.06 m泄漏孔径下的泄漏最大速度高于0.04 m泄漏孔径下的泄漏最大速度,与此同时,0.06 m泄漏孔径下的射流在外部影响范围明显大于0.04 m的情况。
(2)在不同风速下的气体喷射速度分布明显不同,射流从泄漏孔径中心位置喷出,然后进入到外部空间,射流以扇形扩展,其速度分布以扇形中心角处为最大。随着风速的变大,燃气泄漏喷射射流与X轴正方向的夹角不断变小,同时射流在X轴正方向偏转程度变大。
2.2 模拟风速与泄漏孔径对泄漏甲烷浓度影响分析
通过FLUENT模拟计算得到不同风速条件下泄漏孔径0.04m时泄漏甲烷浓度分布云图如图5所示,泄漏孔径0.06m时泄漏甲烷浓度分布云图如图6所示。

(a)0m/s

(c)6m/s
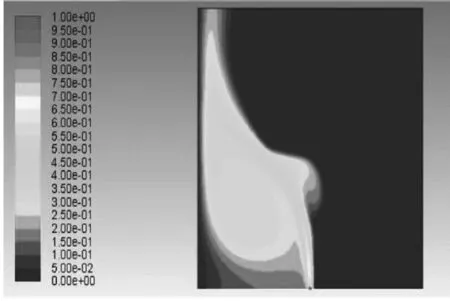
(a)0m/s
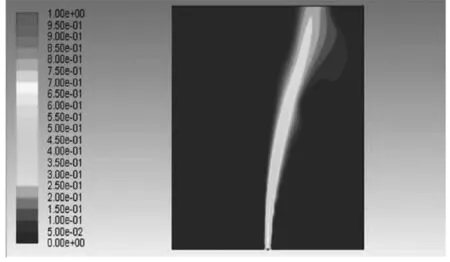
(c)4m/s
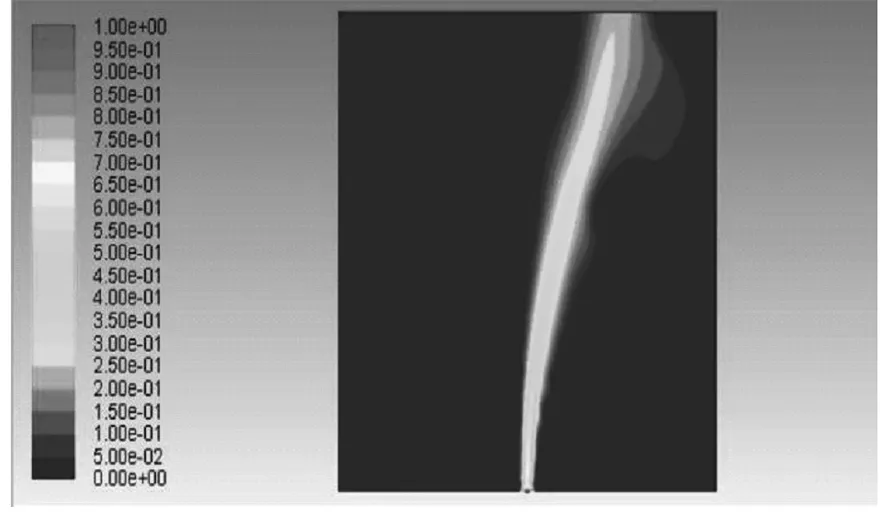
(c)6m/s
通过比较以上6种不同泄漏情况下的甲烷浓度分布云图可知:
(1)燃气管道发生泄漏时,甲烷随来风方向发生扩散,随着扩散时间的增加,甲烷浓度逐渐增加。
(2)在相同泄漏口径时,随着风速的增加,甲烷在X方向上扩散范围增大,Y方向的扩散范围变化不明显,但能达到设定的泄漏高度。
(3)在相同风速条件下,随着泄漏孔径的增大,甲烷在X方向上扩散范围增大,Y方向的扩散范围变化不明显,但能达到设定的泄漏高度。
(4)无论哪种泄漏情况下甲烷浓度在泄漏口附近较密集,但在一定高度后,泄漏气体变得较为稀疏。
3 结论
本文根据燃气管道特性,利用FLUENT对燃气管道发生泄漏的气体扩散问题进行模拟分析,得出甲烷在不同风速不同泄漏孔径下的速度分布云图和甲烷浓度分布云图,研究表明:
(1)燃气管道发生泄漏时,泄漏孔径大小直接影响外部受影响范围的大小,且孔径增大也会造成最大泄漏速度的增大。
(2)燃气管道泄漏流场速度分布受到外部环境的风和泄漏孔径的影响,其流动最大速度位于泄漏孔径中心位置,且风速影响着外部气体与X轴正方向的偏转幅度,同时风速增大射流偏转幅度越大。
(3)燃气管道泄漏口附近气体泄漏速度较快,气体扩散近似自由射流,甲烷浓度分布随着风速的增加和泄漏孔径的增大,在X方向上扩散范围增大明显。
(4)燃气管道在泄漏口处甲烷浓度分布较密集,气体携带较大的动量,此时外部环境中的风对其浓度影响不大,而泄漏气体动量会随着扩散高度增加逐渐减小,外部环境中风的影响则逐渐明显。
参考文献
[1]程猛猛,赵 玲,吴 明,等.架空天然气管道泄漏扩散数值模[J].辽宁石油化工大学学报,2013,33(3):32-34.
[2]朱伯龄,於孝春,李育娟.气体泄漏扩散过程及影响因素研究[J].石油与天然气化工,2009,38(4):354-358.
[3]桑 博,兰惠清,余学立,等.燃气管道泄漏过程模型的研究进展[J].油气储运,2011,30(8):608-613.
[4]刘 欣.可燃气体泄漏扩散的CFD模拟研究[D].天津:天津大学化工学院,2011.
[5]Manabu Kotani,Masanori Katsura,Seiichi Ozawa.Detection of gas leakage sound using modular networks for unknown environments[J]. Neurocomputing,2004 (62):427-440.
[6]Shimanskiy S,T lijima,Nao T.Development of microphone leak detection[J].Technology on Fugen NPP.Progress in Nuclear Enery,2003,43(1):357-364.
