基于非单点模糊RBF网络的判决反馈均衡器

毛忠阳 刘敏 刘云飞 刘锡国

(1. 海军航空工程学院电子信息工程系, 烟台 264001;2. 中国电子设备系统工程公司,北京 100000)

基于非单点模糊RBF网络的判决反馈均衡器

毛忠阳1, 2刘敏1刘云飞1刘锡国1

(1. 海军航空工程学院电子信息工程系, 烟台 264001;2. 中国电子设备系统工程公司,北京 100000)

提出了一种具有较强抗突发干扰能力的非单点模糊径向基函数(Radial Basis Function,RBF)网络判决反馈均衡器．该方法将具有前置滤波特性的非单点模糊化技术引入RBF网络,利用梯度下降法自适应调整参数．通过仿真实验,并与基于径向基函数网络的判决反馈均衡器(Radial Basis Function Network-Decision Feedback Equalizer,RBFN-DFE)和传统判决反馈均衡器(Decision Feedback Equalizer,DFE)进行比较,结果证明该方法抗突发干扰能力强,误码性能好．

均衡器;判决反馈;突发干扰;非单点模糊系统;神经网络

DOI 10.13443/j.cjors.2016110101

引 言

在无线高速数字传输系统中,常常会面临严重的非线性信道畸变,需要高性能的非线性均衡器．非线性均衡器主要有最大似然序列估计均衡器(Maximum-Likelihood Sequence Estimation,MLSE)和判决反馈均衡器(Decision Feedback Equalizer,DFE)． MLSE是理论上的最优均衡器,但运算量和存储量巨大,难以满足工程应用要求;DFE 结构简单,易于工程实现,是广泛采用的非线性均衡器结构,但有误差传递的缺点,在突发干扰条件下性能严重下降．因此,研究性能优良的新型非线性均衡器一直是通信信号处理领域的一个热点问题．

根据Messerschimitt的码间干扰(Inter-Symbol Interference,ISI)空间几何理论[1],信道的均衡问题可以转化为分类问题[2],利用具有良好的非线性分类能力的神经网络来设计新型非线性均衡器是近年来十分活跃的研究领域[3-9]． Chen, Zhang和Yee等人在基于神经网络的非线性均衡问题上作了很深入的研究,大量实验证明其效果能够逼近于MLSE[6-7]．由于径向基函数网络(RadialBasisFunctionNetwork,RBFN)只有一个隐节点层,在结构上比较简单,加上信道均衡的Bayesian方法与RBFN又有很相近的关系[7-8],所以基于RBFN的均衡算法被视为最有前途的神经网络均衡算法[8]．对采用判决反馈结构的RBFN均衡器(RadialBasisFunctionNetwork—DecisionFeedbackEqualizer,RBFN-DFE)的仿真分析表明,RBFN-DFE的误码性能明显优于前馈RBFN均衡器,逼近最优均衡器[7-9]．但判决反馈结构存在抗突发干扰能力差的问题．文献[10]研究表明,当信道由于突发的衰落、干扰等因素影响,使信噪比(Signal-NoiseRatio,SNR)突然下降到5dB以下,并维持几十甚至几百个码元,采用判决反馈结构的均衡器将失去作用,且完全丧失跟踪能力,无法自动恢复到正常工作状态．因此,有必要研究如何提高RBFN-DFE的抗突发干扰能力．

本文从提高径向基函数(RadialBasisFunction,RBF)网络的自适应抗噪声能力出发,将具有前置滤波特性的非单点模糊化技术引入RBF网络,提出具有抗突发干扰能力的改进型RBFN-DFE——基于非单点模糊RBF网络的判决反馈均衡器(Non-SingletonFuzzinessRadialBasisFunctionNetwork-DecisionFeedbackEqualizer,NSFRBFN-DFE)．我们采用NSFRBFN-DFE、RBFN-DFE和传统DFE进行了仿真实验,结果证明NSFRBFN-DFE具有优良的非线性均衡能力和抗突发干扰能力．

1 基于非单点模糊RBF网络的判决反馈均衡器(NSFRBFN-DFE)设计

信道均衡基带模型如图1所示．

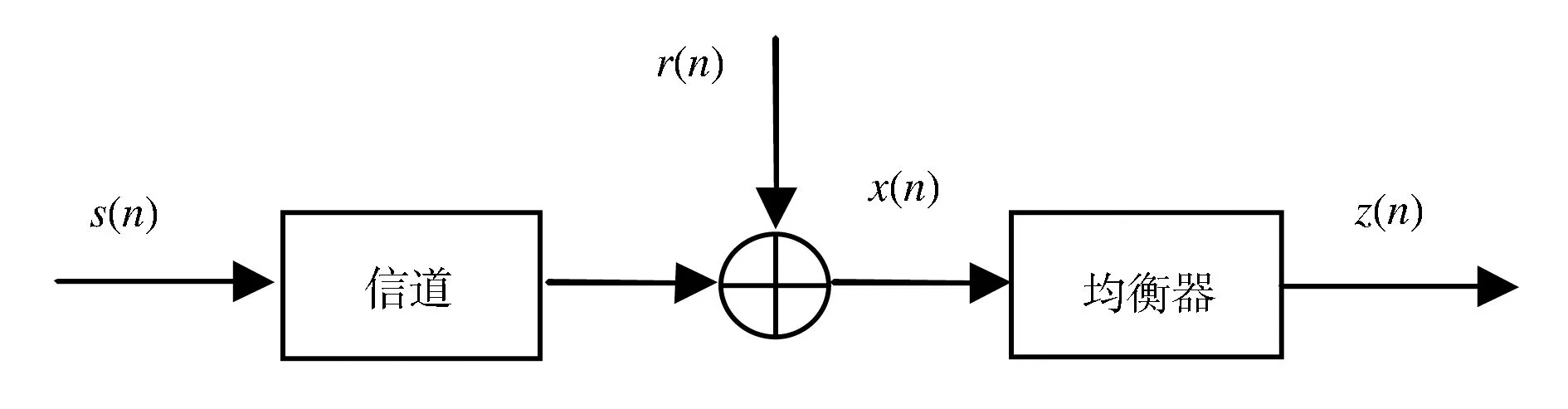
图1 信道均衡模型图

图1中s(n)表示发送信号,x(n)表示信道传输后的畸变信号,z(n)表示均衡器的判决输出信号,r(n)表示信道噪声．信道的含义包括了发送端滤波器、传输介质(媒体)、接受端滤波器及其它元件．均衡器的作用就是要使其判决输出信号z(n)同发送信号s(n)相比,误码率达到最小．判决反馈(Decision Feedback,DF)是工程中常用于抗深度衰落的一种非线性均衡器结构,采用前向单元均衡信道的前导失真,反馈单元抵消后尾失真,具有抽头数少,受定时相位变化影响小,对舍入误差不敏感的优点,且易于工程实现．但DFE存在判决误差反馈传递的问题,在低信噪比条件下无法正常工作,这也是RBFN-DFE抗突发干扰能力差的问题根源．如果设法提高均衡器的自适应抗噪声能力,降低判决误差,便可提高RBFN-DFE的抗突发干扰能力．

1.1 算法结构分析

RBFN-DFE的核心是RBF网络,其性能基本完全由RBF网络决定．RBF网络本质上可视为某些基函数的线性组合,这与模糊系统非常相似．根据Buckley J.J.等人的研究,当模糊系统采用高斯隶属度函数、单点模糊化和取中心反模糊化器时,与正则化RBF网络等价[11]．因此,采用RBF的正则化网络与模糊系统具有天然的相容性,易于结合．非单点模糊化技术是Zadeh提出的,其能赋予模糊系统前置滤波特性,提高系统的自适应抗噪声能力[12]．我们将非单点模糊化技术引入正则化RBF网络(称其为非单点模糊RBF网络,简称NSFRBFN),赋予RBF网络前置滤波特性,改善RBFN-DFE的抗突发干扰能力(称这种改进后的算法为NSFRBFN-DFE)．首先直接给出本文设计的NSFRBFN-DFE结构,如图2所示．

图2 NSFRBFN-DFE结构图

由图2可见,NSFRBFN-DFE的输入为:

X(n) =[x(n)T,z(n)T]T

=[x(n),…,x(n-L+1),z(n-M),

…,z(n-1)]T.

(1)

式中:x(n)=[x(n),…,x(n-L+1)]T,表示畸变信号x(n)的L个延迟;z(n)=[z(n-M),…，z(n-1)]T,表示判决反馈信号z(n)的M个延迟．z(n)在引导阶段由期望信号d(n)给出,在判决阶段是根据y(n)由符号函数得到．

根据模糊系统与正则化RBF网络的相似性,NSFRBFN的输入输出关系可用模糊规则表述如下:

Theny(n) isGl.

(2)

模糊化单元的作用是将确定的输入X(n)映射为输入空间U上的一个模糊集合A′．对于单点模糊化,A′为模糊单值,则对X(n)=X(n*),有uA′(X(n*))=1,而对其余X(n)≠X(n*),有uA′(X(n))=0．但在非单点模糊化中,uA′(X(n*))=1,随着X(n)偏离X(n*),uA′(X(n))逐渐减少,被映射成模糊数,模糊隶属函数与X(n)相关,则有:uA′(X(n))=uX(n)1(X(n)1)★…★uX(n)L+M(X(n)L+M).

(3)

本文采用sup-★(★取代数积算子)合成运算,则有:

(4)

本文取隶属度函数为高斯函数,求解sup[·]得:

(5)

将sup[·]的解式(5)代回式(4),便完成了输入信号的非单点模糊化．再经过正则化单元,并经过加权平均过程,便得到NSFRBFN-DFE的输入输出关系如下(设输入信号x(n)和z(n)分别具有相同的不确定性,为σx和σz):

(6)

z(n)=sign(y(n)) .

(7)

1.2 抗噪声性能分析

在工程处理中,用精确输入X(n*)k代替模糊输入集合的均值mX(n)k,并假设σx=σz=σX(n),式(5)变为:

(8)

(9)

1.3 内部参数学习算法

(10)

(11)

wl(n+1)=wl(n)+ηwψ(e(n))Pl(X(n)) ;

(12)

(13)

(14)

(15)

(16)

(17)

(18)

在仿真实验中,对内部参数的初始值采用减法聚类的方法确定,对所有步长ηw、ηmx、ηmz、ησx、ησz、ηx、ηz简单地采用定步长．

2 仿真实验

根据图1所示的信道均衡模型,仿真实验的线性信道模型取式(19):

(19)

非线性信道模型取式(20):

(20)

式中,ai为信道系数,发送信号s(n)取2-PAM信号,附加噪声r(n)取高斯白噪声．

设计一种线性时变信道(非最小相位信道)和一种非线性时变信道,取信道系数为(利用MATLAB的信号处理工具箱产生信道时变系数ar)[13]:

[B,A] =butter(2,0.2) ar

=filter(B,A,beta·randn(1,Num)).

其中butter()产生一个截止频率为0.2的二阶低通Butterworth滤波器;filter()产生一组有色高斯噪声．

线性信道1:

a=[a0,a1,a2,a3,a4]T

=[0.227+ar,0.466+ar,0.688+

ar,0.466+ar,0.227+ar]T.

非线性信道2:

a=[a0,a1,a2]T

=[0.3482+ar,0.8704+ar,0.3482+ar]T.

用NSFRBFN-DFE、RBFN-DFE和DFE三种算法分别对信道进行均衡实验．实验中前馈单元抽头数L=3,反馈单元抽头数J=2,窗口长度N=40,获取数据延迟d=0,输出信号无延迟,beta=0.2;引导阶段训练序列长度取100个码长,测试阶段用Num=106个数据进行传输测试,独立运行10次后取平均结果．从实验数据分析看,结果偏离均值不大,趋势较为统一,进一步加大独立运行次数对结果影响不大．

2.1 比特误码率(Bit Error Ratio,BER)曲线分析

为了全面考察NSFRBFN-DFE的性能,我们分别在两个信道中,采用相同的数据输入和均衡算法,测出NSFRBFN-DFE、RBFN-DFE和DFE的BER 与SNR 曲线,如图3所示．

(a)信道1 (b)信道2图3 不同算法的均衡效果比较图

从图3中可以看到,在SNR较高时(信道1中SNR>17 dB,信道2中SNR>12 dB),NSFRBFN-DFE同RBFN-DFE的BER曲线是近似相同的,比DFE的BER大约要低1个数量级;当SNR较低时(信道1中SNR<17 dB,信道2中SNR<12 dB),NSFRBFN-DFE比RBFN-DFE和DFE的BER大约要低1个数量级．Mulgrew B.在文献[8]中已经指出,RBFN-DFE的BER曲线是逼近Bayesian最优均衡器的．这说明NSFRBFN-DFE不仅在高信噪比条件下工作时,性能接近最优均衡器,具有优良的非线性均衡能力;而且由于引入非单点模糊化技术所具有的抗噪声能力,在信噪比严重下降时(发生突发干扰),抗突发干扰能力比RBFN-DFE和DFE将有很大提高．为了进一步证明NSFRBFN-DFE优越的抗突发干扰能力,下面进行抗突发干扰实验．

2.2 抗突发干扰能力分析

在两个信道中,设信噪比SNR=24 dB,但在数传过程中从第na=300个码元开始,信道受到突发干扰,SNR突然下降到5 dB,在第nb个码元后信道恢复,以后一直保持信噪比SNR=24 dB．测出在不同的突发干扰持续时间(发生突发干扰的码元长度Nba=nb-na)下,NSFRBFN-DFE、RBFN-DFE、DFE的BER曲线,如图4所示．

(a)信道1 (b)信道2图4 不同算法的抗突发干扰能力比较图

由图4可见(RBFN-DFE和DFE的Nba-BER曲线是基本重合的),在信道1、2中,RBFN-DFE和DFE仅仅能够在几十个码元长度的突发干扰下正常工作(BER<10-3),而NSFRBFN-DFE在Nba<180内都能正常工作．这充分说明,NSFRBFN-DFE具有优越的抗突发干扰能力．

2.3 计算复杂度分析

三种均衡算法的计算复杂度比较见表1．(设RBF网络的隐层单元数目为S,且考虑重复计算单元用存储器处理)．

表1 计算复杂度比较

由表1可见,NSFRBFN-DFE的计算开销增加不大．

3 结 论

本文提出了一种基于非单点模糊RBF网络的判决反馈均衡器,详细论述了其设计方法,并分析了其抗突发干扰的原理．仿真实验结果证明,该算法具有较强的抗突发干扰能力,在复杂环境下的无线通信系统中有较好的应用前景．从NSFRBFN-DFE的算法结构和计算复杂度分析可见,该算法易于工程实现．着手NSFRBFN-DFE的现场可编程门阵列(Field Programmable Gate Array,FPGA)实现和真实信道实验是我们下一步的工作．

[1] MESSERCHIMITT D G. A geometric theory of intersymbol interference[J]. The Bell system technical journal, 1973, 52(9):1483-1539.

[2] GIBSON G J, SIU S, COWAN C F N. The application of nonlinear structures to the reconstruction of binary signals[J]. IEEE transactions on signal processing, 1991, 39(8): 1877-1885.

[3] WENG W D, YEN C T. Reduced-decision feedback FLANN nonlinear channel equalizer for digital communication systems[J]. IEE proceedings: communications, 2004, 151(4): 305-311.

[4] DENG J P, SUNDARARAJAN N, SARATCHANDRAN P. Communication channel equalization using complex-valued minimal radial basis function neural networks[J]. IEEE transactions on neural networks, 2002, 13(3): 687-696.

[5] BURSE K, YADAV R N, SHRIVASTAVA S C. Channel equalization using neural networks: a review[J]. IEEE transactions on signal processing, 2010, 40(3): 352-357.

[6] CHEN S, MCLAUGHLIN S, and MULGREW B. Complex valued radial basis function networks: application to digital communications channel equalization (partⅡ)[J]. Signal processing, 1994, 36(2): 175-188.

[7] YEE M S, YEAP B L, HANZO L. Radial basis function-assisted turbo equalization[J]. IEEE Transactions on communications, 2003, 51(4): 664-675.

[8] MULGREW B. Applying radial basis functions[J]. IEEE signal processing magazine,1996, 13(2): 50-65.

[9] 王军锋, 褚骁勇, 宋国乡. 基于RBF神经网络的自适应均衡器研究[J]. 信号处理, 2002, 18(3): 199-201.

WANG J F, CHU X Y, SONG G X. Study on new adaptive equalizers based on RBF neural networks [J]. Signal processing, 2002,18(3):199-201.(in Chinese)

[10]何平, 徐炳祥, 张辉, 等. 时变衰落信道下的自适应均衡技术[J]. 电子学报, 1993, 21(4): 85-89.

HE P, XU B X, ZHANG H, et al. Adaptive equalization technique application to time-variant fading channels[J]. Chinese journal of electronics, 1993, 21(4): 85-89.(in Chinese)

[11]王士同. 模糊系统、模糊神经网络及应用程序设计[M]. 上海: 上海科学技术文献出版社, 1998.

WANG S T. Fuzzy systems, fuzzy neural network and application design[M]. Shanghai: Shanghai Scientific and Technological Literature Press,1998.

[12]王立新. 王迎军, 译. 模糊系统与模糊控制[M]. 北京: 清华大学出版社, 2003.

[13]祖家奎, 赵淳生, 戴冠中. 非单点模糊逻辑系统在非线性信道均衡中的应用[J]. 控制与决策, 2004, 19(4): 407-415.

ZU J K, ZHAO C S, DAI G Z. Nonlinear communications channel equalization based on non-singleton fuzzy logic system[J]. Control and decision, 2004, 19(4): 407-415.(in Chinese)

[14]NAMYONG K. Step-size control for width adaptation in radial basis function networks for nonlinear channel equalization[J]. Journal of communications and networks, 2010, 12(6): 600-604.

[15]HARISH K S,BASABDATTA M. Adaptive decision feedback equalizer for SISO communication channel using combined FIR-neural network and fast block LMS algorithm[C]//2016 IEEE Annual India Conference (INDICON), December 16-18, 2016.

[16]ZERDOUMI Z, CHIKOUCHE D, BENATIA D. Adaptive decision feedback equalizer based neural network for nonlinear channels [C]//3rd International Conference on Systems and Control, October 29-31 2013.

毛忠阳 (1979—),男,河南人,海军航空工程学院副教授,博士,中国电子设备系统工程公司博士后,研究方向为现代通信理论与应用.

刘敏 (1983—),女,山西人,海军航空工程学院讲师,博士,研究方向为通信信号处理.

刘云飞 (1983—),男,山东人,海军航空工程学院青岛校区讲师,硕士,研究方向为通信信号处理.

A decision feedback equalizer based on non-singleton fuzzy RBF network

MAO Zhongyang1,2LIU Min1LIU Yunfei2LIU Xiguo2

(1.DepartmentofElectronicInformationEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China; 2.ChinaElectronicSystemCorporation,Beijing100000,China)

A non-singleton fuzzy radial basis function(RBF) network based decision feedback equalizer is proposed in this paper for severely nonlinear distorted channels with burst jamming. The method introduced non-singleton fuzzy technology with preceding filtering capability into RBF network, and adjusted the tunable parameters by gradient-descent algorithm. Simulation is carried out to compare it with other nonlinear channel equalizers. The result shows the method has better performance on anti-burst jamming and bit error rate.

equalizer; decision feedback; burst jamming; non-singleton fuzzy system; neural network

2016-11-01

中国博士后科学基金特别资助(2016T91018)；国家自然科学基金资助课题(60772056)

10.13443/j.cjors.2016110101

TN929.5

A

1005-0388(2017)01-0084-06

联系人： 毛忠阳 E-mail:freedom_mzy@163.com

毛忠阳, 刘敏, 刘云飞, 等. 基于非单点模糊RBF网络的判决反馈均衡器[J]. 电波科学学报,2017,32(1):84-89.

MAO Z Y, LIU M, LIU Y F, et al. A decision feedback equalizer based on non-singleton fuzzy RBF network [J]. Chinese journal of radio science,2017,32(1):84-89. (in Chinese). DOI: 10.13443/j.cjors.2016110101