基于权值约束变换误差的虚拟阵列波束形成

胡丹婷 耿军平 梁仙灵 朱卫仁 金荣洪,2 庄凯杰

(1.上海交通大学电子工程系,上海 200240; 2. 微米/纳米加工技术国家级重点实验室,上海 200240)

基于权值约束变换误差的虚拟阵列波束形成

胡丹婷1耿军平1梁仙灵1朱卫仁1金荣洪1,2庄凯杰1

(1.上海交通大学电子工程系,上海 200240; 2. 微米/纳米加工技术国家级重点实验室,上海 200240)

针对内插变换应用于波束形成时,适用角度范围受限的问题,提出了一种利用权值约束变换误差的改进算法.该方法将权值和变换误差约束为近似正交的关系,在虚拟阵列接收信号的协方差矩阵上加载变换误差协方差矩阵,改善了变换误差过大时波束形成性能下降的问题.仿真结果表明,改进后的算法应用于大角度内插变换波束形成时,在干扰处仍能形成稳定的较深的零点,增加了虚拟阵列波束形成的输出信干噪比 (Signal to Interference and Noise Ratio, SINR).与现有方法相比,该方法增加了内插变换应用于虚拟阵列波束形成时的适用角度范围,且能够补偿阵列本身带来的误差,计算复杂度较低.

内插变换;波束形成;变换误差; 近似正交; 波束形成性能

DOI 10.13443/j.cjors.2017011201

引 言

近年来,虚拟天线技术应用于波达方向(Direction of Arrival, DOA)估计[1]和波束形成[2]的研究备受关注. 其中,Friedlander B等[3]在20世纪90年代提出的内插变换技术最早应用于DOA估计中,因为具有计算简单,适用性强等优点,此后内插变换技术应用于虚拟阵列DOA估计的研究得到了人们的广泛关注[4-6],近几年开始有学者将内插变换技术应用于虚拟阵列波束形成的研究中. 内插变换能够将任意实际阵列接收到的数据转换到所需的阵列中,使得现有的一些算法得以应用;且具有对阵列本身的误差进行补偿的特点,进而能消除互耦等因素带来的影响[7];此外,还可以改变阵列的自由度等. 然而,内插变换对虚拟阵的阵列形式要求较高,且适用角度范围受到变换误差的限制. 杨鹏等[8]通过仿真实验,给出变换误差和虚拟阵列设置的关系,并指出当观测区域大于60°时,变换误差随着观测角度范围的增加而迅速增加. 此时,将内插变换应用于虚拟阵列波束形成中,会出现干扰点处零陷变浅甚至偏移的问题.

针对内插变换“角度敏感”的问题,有学者提出了多区域内插法[3],将变换范围划分为多个区域分别处理. 但该方法过程较为繁琐,并且会降低自由度. 因此,很多学者进行了更加深入的研究.

针对内插变换应用于DOA估计时的角度范围受限问题,很多改进的方法被提出[9]. Markus等人[10]提出了一种基于流形长度的虚拟天线阵,可以在较大区间内插值变换,但是需要求解新的阵列导向矢量,求解较复杂. Hyberg P等人[11-12]通过约束角度估计误差,推导出最优转换矩阵,该方法的最优转换矩阵求解需要计算DOA估计代价函数沿虚拟阵列信号特征向量方向的梯度,计算复杂度高.

针对内插变换应用于波束形成时角度范围受限的问题,研究较少. 现有的研究主要建立在来波信号的角度处于变换区域内,且变换区域误差满足一定门限的基础上. 当来波信号角度处于更大的范围,则由于变换区域的增加,变换误差随之增大. 此时经过大角度范围的内插变换后进行波束形成,不仅达不到补偿误差或者提高输出信干噪比 (Signal to Interference and Noise Ratio, SINR)的作用,还会出现干扰点处零点变浅甚至偏移的问题.

数值计算方法中,正交加权是控制数值计算误差的有效手段. 针对内插变换应用中,变换误差过大导致的波束形成性能下降的问题,本文提出将权值和变换误差约束为近似正交的关系,在信号的协方差矩阵上加载误差协方差矩阵的方法,以约束变换误差对波束形成性能的影响. 与现有方法相比,该方法大大提高了内插变换应用于波束形成时的适用角度范围,同时减弱了对虚拟阵阵列形式的过多要求. 本文在考虑互耦等情况下,对改进的算法进行了仿真分析. 结果表明,该方法能在增加适用角度范围的同时,补偿阵列本身带来的误差.

1 阵列流形和信号模型

1.1 阵元为理想点源的接收信号模型

为了简化分析,仅考虑方位角平面,以θ表示方位角方向.因为方法不受阵列形式的约束,所以考虑一个由M1个理想点元构成的一般阵列,该阵列在θ处的阵列响应矢量表示为a(θ),为M1×1的矢量.假设一个远场窄带信号s(t)和p个干扰信号ik(t),(k=1,2,…,p)入射到该阵列,则M1×1的接收信号矢量x(t)的数学模型可以写成:

=AS(t)+n(t).

(1)

1.2 考虑阵元方向图和互耦的接收信号模型

在1.1节的信号模型分析中,假设各阵元相对于其他阵元独立工作且各向同性. 然而,实际单元往往是定向单元,且阵元间的互耦效应在阵列天线的实际工作中常常是不可避免的.

考虑方向图和互耦的时候,式(1)中的阵列接收数据模型为:

x(t)=C[F·A]S(t)+n(t).

(2)

式中:F为M1×(k+1)的辐射方向图矩阵,第(m,n)个元素代表第m个单元对第n个信号的响应;C为M1×M1的阵列单元耦合矩阵. 此时的真实阵列流形矩阵为C[F·A].

阵元间互耦存在时, 由于阵元入射开路电压的二次反射, 阵元的输出电压变为阵元开路电压以相应的互耦系数为权系数的线性叠加. 互耦矩阵求解方法为[13]:

C=(Z/ZL+I)-1.

(3)

式中:

真实阵列接收信号协方差矩阵R为:

R=E{x(t)x(t)H}.

(4)

式中:E{·}表示期望;H表示共轭转置.

2 阵列转换及误差分析

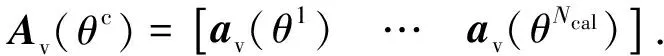
真实阵列和虚拟阵列之间的变换矩阵为:

(5)

式中:‖·‖F为Frobenius模;矩阵B表示虚拟阵列与真实阵列之间这种变换关系,为虚拟变换矩阵.

当变换范围内插值抽样点数大于真实阵列的阵元数,且真实天线阵的阵列流形矩阵A(θc)为满秩,通过最小二乘法求得真实阵列和虚拟阵列之间的变换矩阵:

B=Av(θc)AH(θc)(A(θc)AH(θc))-1.

(6)

变换误差矩阵为:

ΔE=BA(θc)-Av(θc),

(7)

在任意角度θ处,变换误差Δe(θ)=Ba(θ)-av(θ).

定义变换误差为:

(8)

虚拟阵列中接收信号模型为:

xv(t)=Bx(t).

(9)

利用真实阵列流型与虚拟阵列流型之间的变换矩阵,将真实阵列输出转换为虚拟阵列输出,总是存在变换误差.变换误差取决于真实阵列及对应的虚拟阵列设置,以及内插变换的精度及变换角度范围.

假设真实阵列采用如图1所示的圆阵[8],圆阵半径r=1.28λ(λ表示波长),选取16单元圆阵中1-9号阵元.

为了与实际相结合同时简化分析,阵列建模时,用有向单元代替点源,同时考虑互耦的影响.采用的单元方向图为cosφ,单元仅向外辐射,且不考虑极化,考虑曲面的遮挡效应;对于任意单元,只考虑与之相邻的2个单元间距内阵元的互耦影响,互耦矩阵如式(3)所示. 其中单元自阻抗和互阻抗在CST中用对称振子组阵求得,对称振子臂长39.88 mm,半径2 mm,两臂间距0.24 mm,离散端口馈电电阻50Ω,互耦矩阵中的Z/ZL对应值为:

值得注意的是,阵列建模中,方向图和互耦矩阵的引入,是为了验证本文提出的算法在该情况下的有效性,其取值并不会影响对算法有效性的验证.本文的数据仅作为理论分析的参考值.

此外,选择x轴正向为角度θ参考轴,逆时针方向为正方向.

图1 真实阵列及虚拟线阵示意图

虚拟线阵单元为各向同性,单元数为5,阵元间距d=0.5λ,虚拟线阵距离x轴为h=0.82λ,如图1所示. 变换范围从20°至180°,区间变换步长为0.1°,此时变换误差与变换角度范围的变化关系如图2所示.

图2 变换角度范围和变换误差关系

从图2中可以看出：随着变换角度范围的增加,内插变换误差增加,在变换角度范围小于60°时,变换误差在6.3×10-4以下;角度范围大于60°时,变换误差迅速增大;当变换角度范围大于100°时,显然变换误差很大,在180°处,接近0.50.

从上面的分析可知,在变换角度范围过大时,内插变换误差的影响不可忽略.本文接下来的分析中,通过对最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)算法权值计算公式及阵列响应误差的分析,将权值和误差约束为近似正交的关系,减小变换误差对虚拟阵列响应的影响.

3 算法及改进权值计算

MVDR波束形成器是在控制信号分量无失真地通过滤波器的情况下,最小化输出功率,从而使得无用信号所贡献的功率最小. 将MVDR算法应用于虚拟阵列中,并且分析变换误差对权值计算中的影响:

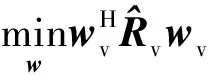
(10)

(11)

式中，L是采样快拍数.

权值解为:

(12)

加权后的输出为:

(13)

根据上文的描述,可知角度θ处对应的虚拟阵列空间响应偏差表达式为:

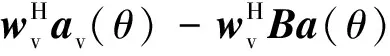
(14)

式(14)中,如果将权值wv约束为与变换误差Δe(θ)正交,则可以减少空间响应偏差.

(15)

令

ΔRE=ΔEΔEH,

(16)

式中,ΔRE在本文中称为误差协方差矩阵.则此时式(15)转化为:

(17)

同时考虑权值的相关条件式(10)和式(17),则改进后的利用加载误差协方差矩阵来约束空间响应误差的表达式为:

(18)

α为[0,1)之间的常数,α取值越大,式(18)求解出的权值与误差的正交性越好;但是α过大会使加载量过大而降低干扰抑制的性能.

图3为不同的输入信噪比时,G(Θ)随α的变化曲线. 保证权值与误差矩阵的列有较好的正交性,即G(Θ)尽可能小的同时,α的取值尽可能小.

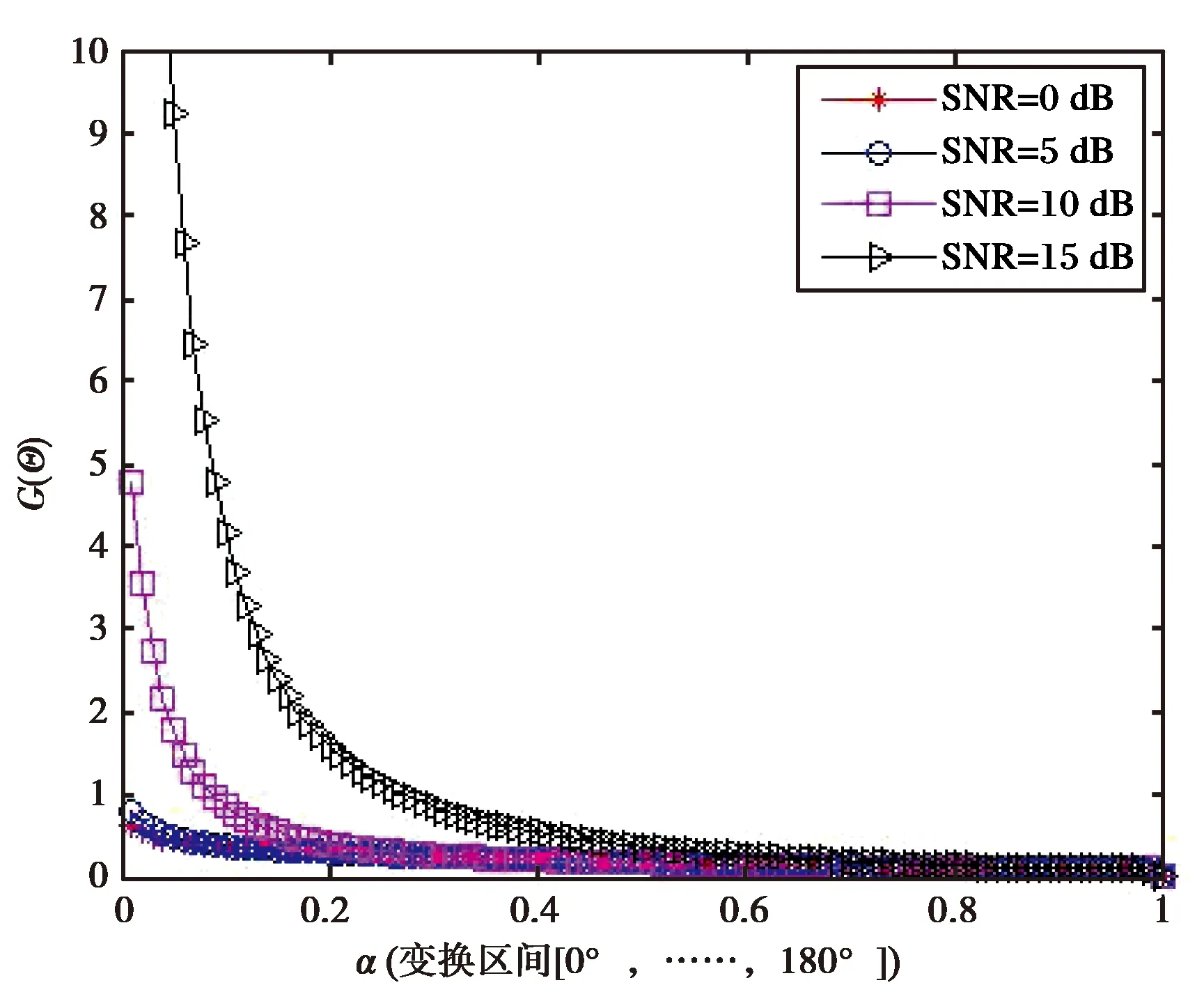
图3 G(Θ)随不同α的变化曲线图

式(18)中,相当于在信号的协方差矩阵上加载了一个误差的协方差矩阵,变为:

(19)

这也是本文提出的权值和内插变换误差近似正交方法的实现方式.

改进后的权值解为:

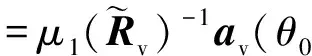
(20)

加权后的输出为:

(21)

4 算法步骤总结

根据所提出的改进方法,再参考内插变换虚拟阵列波束形成的过程,算法步骤总结如下:

2) 确定真实阵列在Θ上Ncal个抽样点处真实阵列响应矢量构成的真实阵列流形矩阵:

在实际情况下,真实阵列响应矢量应包含方向图和互耦影响,如式(2)所示;

3) 根据所假设的虚拟阵列,得到虚拟阵列在Θ上Ncal个抽样点处虚拟阵列响应矢量构成的虚拟阵列流形矩阵:

4) 根据式(6)得到变换矩阵B,再根据式(7)得到变换误差矩阵ΔE;

6) 根据式(20)求出权值wv,进行波束形成.

5 仿真及结果分析

本文通过几组仿真实例验证所提出的改进算法的有效性. 另外,仿真条件的设置参考了文献[7].

1) 仿真实验一:变换角度范围较小的情况

图4 真实阵列和虚拟线阵四种方法波束形成对比图(变换范围为

图4中,理想情况作为其他几种方法的参照,阵元是各向同性,且不考虑互耦及载体曲面的遮挡时的圆阵波束形成结果.

考虑互耦情况为,在接收信号中存在互耦影响时,圆阵波束形成结果;为了与虚拟线阵波束形成的互耦补偿效果对比,该波束形成过程中未对互耦进行补偿. 如图所示,在干扰1(65°)和干扰2(140°)处,零陷变浅,无法实现对干扰的有效抑制.

内插变换方法为将实际情况接收信号数据变换到虚拟线阵中的波束形成结果;本文提出的方法是在内插变换方法的基础上,将权值和变换误差约束为近似正交关系的波束形成结果.

在变换范围较小的情况下,内插变换法和本文提出的方法都能在变换范围内(60°～120°)很好地实现波束形成. 如图所示,在变换角度较小的情况时,两种方法的结果曲线几乎重合. 在干扰1(65°)处形成稳定的,较深的零陷(约-48 dB);而在变换范围外,波束形成的效果较差,干扰2(140°)处,零陷变浅(约-30.5 dB).

2)仿真实验二:变换角度范围较大情况

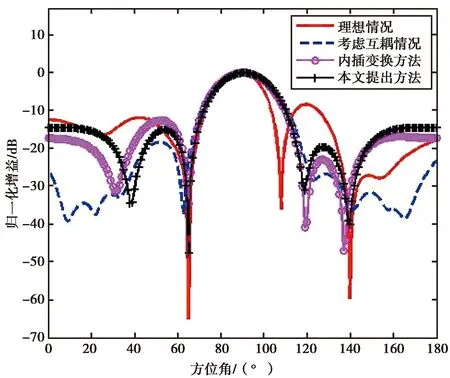
图5 真实阵列和虚拟线阵四种方法波束形成对比图(变换范围为

如图5所示,在变换角度范围较大的情况下,变换误差变大,此时变换误差的影响不可忽略. 因此,采用原来的内插变换波束形成的方法时,变换误差过大导致了波束形成性能的下降. 干扰点(65°)处零陷变浅(约-34 dB),干扰点(140°)处零陷偏移(在干扰点处约-31 dB);而改进后的权值约束误差的方法依然能很好地实现对互耦带来的误差的补偿,在干扰点65°和140°处都能形成稳定的,较深的零陷(分别约为-48 dB、-40 dB).

3)仿真实验三:输出SINR随输入SNR变化

分别对仿真实验一和仿真实验二中的输入SNR进行变化,变化范围0 dB至25 dB,其他条件不变,对比几种波束形成方法的输出SINR的变化.

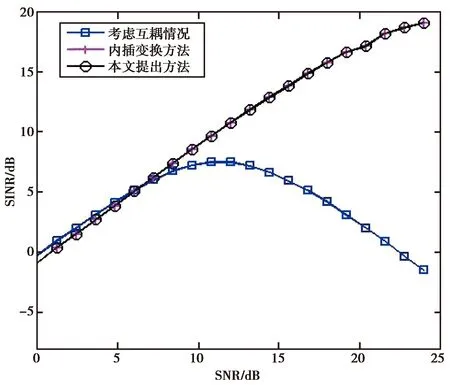
(a) 变换范围为

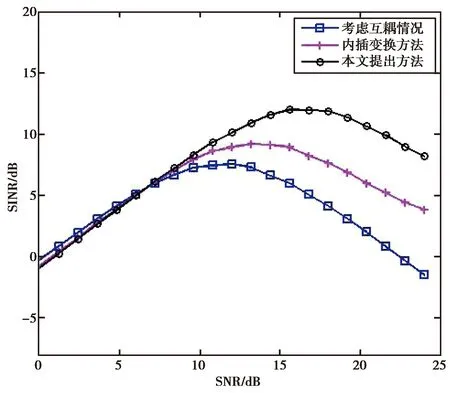
(b) 变换范围为图6 输出SINR随输入SNR变化曲线图

从图6中可以看出,实际情况下,由于互耦的影响,圆阵波束形成中输出SINR结果较差.

4)仿真实验四:虚拟阵列其他设置情况

将虚拟阵元数改为9,且虚拟阵元间距变为d1=0.25λ,其他条件同仿真实验二.

由于虚拟阵列设置不同,此时对应的内插变换误差不同(0.67). 与仿真实验一和仿真实验二相比,变换误差增大,导致内插变换方法的波束形成性能大大下降,而改进后的方法对阵列形式的依赖性相对较弱些.

如图7所示,在虚拟阵元数为9、阵列间距为0.25λ时,采用内插变换的方法进行波束形成,性能大大下降,无法对干扰形成良好的抑制,且输出SINR较差;而改进的方法依然能在干扰处(65°和140°)形成稳定的零点,实现良好的干扰抑制效果. 输出SINR虽然受到变换误差过大的影响,但依然要较内插变换的方法更优.

(a) 波束形成图

(b)输出SINR随输入SNR变化曲线图图7 虚拟阵列在其他设置情况(n1=9,d1=0.25λ)

6 结 论

内插变换方法可以将真实阵列接收到的数据转换到所需要的虚拟阵列中,可以对阵列互耦等误差进行补偿,也可以改变阵列的自由度等,但是存在“角度敏感”的问题. 本文通过加载误差协方差矩阵的方法来约束空间响应误差,可以解决因为内插变换误差较大,虚拟阵列波束形成中产生的干扰处零陷变浅或者偏移的问题,实现内插变换在更大角度范围内波束形成的应用. 而且,这种方法针对变换误差设计,对虚拟阵列的阵列形式要求更低,波束形成性能更好. 本文提出的方法中,真实阵列不受到阵列形状的限制,除了本文所提到的圆环阵,还可以适用于其他阵列.

[1] FRIEDLANDER B, WEISS A J. Direction finding for wide-band signals using an interpolated array[J]. IEEE transactions on signal processing, 1993, 41(4): 1618-1634.

[2] BLOMBERG A E A, AUSTENG A, HANSEN R E. Adaptive beamforming applied to a cylindrical sonar array using an interpolated array transformation[J]. IEEE journal of oceanic engineering, 2012, 37(1): 25-34.

[3] FRIEDLANDER B, WEISS A J. Direction finding using spatial smoothing with interpolated arrays[J]. IEEE transactions on aerospace and electronic systems, 1992, 28(2): 574-587.

[4] FRIEDLANDER B. The root-MUSIC algorithm for direction finding with interpolated arrays[J]. Signal processing, 1993, 30(1): 15-29.

[5] WEISS A J, FRIEDLANDER B, STOICA P. Direction of arrival estimation using MODE with interpolated arrays[J]. IEEE transactions on signal processing, 1995, 43(1): 296-300.

[6] WEISS A J, GAVISH M. Direction finding using ESPRIT with interpolated arrays[J]. IEEE transactions on signal processing, 1991, 39(6): 1473-1478.

[7] YANG P, YANG F, NIE Z P, et al. Robust adaptive beamformer using interpolation technique for conformal antenna array[J]. Progress in electromagnetics research B, 2010, 23: 215-228.

[8] 杨鹏, 杨峰, 聂在平. 基于子阵分割和虚拟内插 ESPRIT 算法的圆柱共形阵 DOA 估计[C]//2009 年全国天线年会论文集 (下), 成都, 2009.

[9] PESAVENTO M, GERSHMAN A B, LUO Z Q. Robust array interpolation using second-order cone programming[J]. IEEE signal processing letters, 2002, 9(1): 8-11.

[10]BUHREN M, PESAVENTO M, BOHME J F. Virtual array design for array interpolation using differential geometry[C]//IEEE International Conference on Acoustics Speech, and Signal Processing , 2004, 2: 229-232.

[11]HYBERG P, JANSSON M, OTTERSTEN B. Array mapping: optimal transformation matrix design[C]//IEEE International Conference on Acoustics Speech, and Signal Processing, 2002, 3: 2905-2908.

[12]HYBERG P, JANSSON M, OTTERSTEN B. Array interpolation and bias reduction[J]. IEEE transactions on signal processing, 2004, 52(10): 2711-2720.

[13]LUI H S, HUI H T, LEONG M S. A note on the mutual-coupling problems in transmitting and receiving antenna arrays[J]. IEEE antennas and propagation magazine, 2009, 51(5): 171-176.

[14]NASIR J, JAMALUDDIN M H, KAMARUDIN M R, et al. A four-element linear dielectric resonator antenna array for beamforming applications with compensation of mutual coupling[J]. IEEE access, 2016, 4: 6427-6437.

耿军平 (1972—),男,陕西人,副教授,主要研究方向为电磁场理论、电磁计算方法、现代天线技术、信号处理等.

梁仙灵 (1978—),男,浙江人,副教授,主要研究方向为现代天线理论与技术、有源相控阵列、DBF阵列等,发表相关学术刊物及会议论文180余篇.

朱卫仁 (1983—),男,浙江人,特别研究员,博士生导师,主要研究方向为人工电磁超材料的理论及实现、基于超材料的天线及射频器件、表面等离子体激元等.

金荣洪 (1963—),男,江苏人,教授、博士生导师,主要研究方向为电磁场理论、现代天线技术、电磁计算方法、天线信号处理、智能天线及相控阵天线等.

庄凯杰 (1993—),男,江苏人,硕士研究生,主要研究方向为电磁场理论,现代天线技术等.

Virtual array beamforming based on the constraint of interpolation mapping errors using orthogonal weights

HU Danting1GENG Junping1LIANG Xianling1ZHU Weiren1JIN Ronghong1,2ZHUANG Kaijie1

(1.DepartmentofElectronicEngineering,ShanghaiJiaotongUniversity,Shanghai200240,China;2.NationalKeyLaboratoryofScienceandTechnologyonMicro/NanoFabrication,Shanghai200240,China)

When the interpolation technology is applied to beamforming, data for a virtual array are required to be obtained using interpolated transformation of real data. However, the interpolation mapping errors will affect the performance of virtual array beamforming, especially at wide angles. In this paper, we present an improved algorithm by optimizing the array weights to constrain the mapping errors. The key feature of this algorithm is keeping the orthogonality between the mapping errors and the weights, which can be achieved by loading the covariance matrix of the mapping errors on that of the signals. By doing this, the beamforming performance of the virtual array can be improved, even for relatively large mapping errors. Numerical simulations confirm the validity of proposed algorithm for wide angle beamforming, which shows stable and deep nulls in the direction of interference, and thus, increases the signal to interference and noise ratio(SINR) of the virtual array beamforming. In comparison with the existing methods, the proposed virtual array beamforming method can compensate the real array errors, and be feasible over wide sectors as well, with lower computational complexity.

interpolation; beamforming; mapping error; orthogonality; beamforming performance

2017-01-12

国家自然科学基金(61571289，61571298，61471240)

10.13443/j.cjors.2017011201

TN821

A

1005-0388(2017)01-0008-08

胡丹婷 (1992—),女,江西人,硕士研究生,主要研究方向为阵列信号处理,自适应波束形成等.

联系人： 耿军平 E-mail：gengjunp@sjtu.edu.cn

胡丹婷, 耿军平, 梁仙灵, 等. 基于权值约束变换误差的虚拟阵列波束形成[J]. 电波科学学报,2017,32(1):8-15.

HU D T, GENG J P, LIANG X L, et al. Virtual array beamforming based on the constraint of interpolation mapping errors using orthogonal weights [J]. Chinese journal of radio science,2017,32(1):8-15. (in Chinese). DOI: 10.13443/j.cjors.2017011201