基于频域数据采样和时域信号同步的超宽带时间反转成像

李元奇 夏明耀

(1.电子科技大学电子工程学院,成都 611731;2.北京大学信息科学技术学院,北京 100871)

基于频域数据采样和时域信号同步的超宽带时间反转成像

李元奇1夏明耀2

(1.电子科技大学电子工程学院,成都 611731;2.北京大学信息科学技术学院,北京 100871)

提出一种基于频域数据取样和时域信号同步的超宽带(Ultrawideband, UWB)时间反转(Time-Reversal, TR)成像方法. 单个发射机发射UWB脉冲信号到探测区域,时间反转镜(Time Reversal Mirror,TRM)的每个天线单元对散射信号进行细频和粗频数据采样,得到各自单元的频率-频率-多站数据矩阵(individual-FF-MDM). 把所有单元的该矩阵堆砌起来,形成一个全体单元的频率-频率-多站数据矩阵(full-FF-MDM),并对full-FF-MDM进行奇异值分解(Singular Value Decomposition, SVD),得到耦合了目标位置信息的左奇异值向量. 将每一个左奇异值向量变换成时域脉冲回传辐射,则来自TRM各单元的回传辐射信号在相应目标处同时到达波形的最大值,而在非该目标处则不能同时达到最大值. 于是,定义各单元的回传信号乘积作为目标成像函数,可获得良好的横向和纵向分辨率.

频域数据采样;奇异值分解;时间反转成像;时域信号同步

DOI 10.13443/j.cjors.2017020501

引 言

时间反转(Time-Reversal,TR)技术[1]是将时间反转镜(Time Reversal Mirror,TRM)接收到的信号在时序上进行反转(先时刻信号变成后时刻信号,后时刻信号变成先时刻信号),它等效于频域上的共轭,然后将时间反转信号回传辐射以定位目标信号源或者目标散射体. 在无耗时不变媒质中,由于波动方程的互易性,时间反转信号在目标位置能实现时空聚焦. 时间反转技术最早在声学中提出,后来也被广泛地应用于电磁场领域[2-4].

时间反转信号的回传辐射既可以在真实媒质中进行,即physical TR,也可以在合成计算域中实现,即synthetic TR. 前者主要应用于无线通信[5]和无线功率合成[6]等领域. 后者的典型应用是目标探测和成像领域,包括地下目标探测[7],穿墙探测[8]和医疗成像[9]. 本文讨论时间反转技术在探测成像领域中的应用.

TRM接收到的多站散射数据形成的矩阵(Multistatic Data Matrix,MDM)称为时间反转算子(Time-Reversal Operator,TRO),TRO的本征值分解构成了时间反转算子分解(Time-Reversal Operator Decomposition, DORT)成像方法[10]和时间反转多信号分类(Time Reversal Multiple Signals Classification,TR-MUSIC)成像方法[11]的基础. 对于DORT方法,当被应用于分离良好的点散射体时,信号子空间的本征值反映了点散射体的散射强度,本征向量耦合了该散射体的位置信息,它们的合成回传辐射脉冲信号能实现散射体的定位成像. DORT既可以用于时谐信号,也可以用于超宽带(Ultrawideband, UWB)信号[10-12],但如果散射体良好分离的条件不能满足,DORT的成像性能将下降. 另一方面,TR-MUSIC方法则利用和信号子空间正交的噪声子空间获得超分辨率成像[11].

传统上,DORT和TR-MUSIC利用的TRO是一个频点处的空间-空间MDM(Space-Space MDM, SS-MDM). 在SS-MDM中,它的第i行第j列的元素对应于由第j个发射单元发射探测信号到目标成像区域、第i个接收单元接收到的散射信号. 多频点的SS-MDM的合成成像是DORT和TR-MUSIC的UWB形式,称为时域DORT(Time Domain,DORT, TD-DORT)[12]和UWB-MUSIC[3].但是,因为在每个频点处通过本征值分解得到的本征向量都带有一个随机的和频率相关的相位,所以TD-DORT需要一个预处理过程来得到相干时域脉冲. 在文献 [13-14] 中,提出了一个替代性方法,它利用空间-频率 MDM(Space-Frequency MDM, SF-MDM)的奇异值分解来直接得到相干时域向量. 这种方法利用不同频率点的散射信号直接形成一个新的MDM,这个MDM的列和行分别对应于接收信号的空间分量和频率分量. 但是,对该MDM进行奇异值分解后得到的耦合了目标位置信息的左奇异向量在不同的频率分量处提供相同的相移信息,这导致在目标位置处回传辐射信号的相干性大大减弱. 此外,DORT 和TR-MUSIC 都需要测量N×N个回波信号来构成SS-MDM,其中N是收发单元的数量,接着要在大量的频点上进行本征值分解,计算负担沉重. 至于SF-MDM方法,虽然避免了在不同频点上的重复性的矩阵分解,但是仍然需要测量N×N个回波信号来形成大小为N×N×P的空间-频率矩阵,其中N是收发单元的数量,P是频率采样点的数量.

文献 [15-17]提出了一种克服上述缺陷的方法,它利用频率-频率MDM(Frequency-Frequency MDM,FF-MDM)的奇异值分解得到的左奇异向量形成相干的回传辐射信号来对目标成像. 在FF-MDM中,每个矩阵元素对应于一个频率点处的接收信号,该频率点由粗频采样和细频采样两部分合成. 在文献[15] 中,使用一个单站收发单元(后向散射数据)来获得一个给定场景的散射信号形成FF-MDM,对其进行奇异值分解(Singular Value Decomposition, SVD),利用左奇异向量的回传辐射得到目标成像图,然后连续改变收发机的位置,将在不同位置获得的成像图相乘得到最终的成像结果.

在本论文中,我们采用单发射单元、多接收单元的方式代替步进移动的单站收发单元. 首先,发射单元发射UWB脉冲信号到探测区域,TRM的所有接收单元记录散射信号;然后,在每个接收单元上对记录信号进行细频和粗频数据采样,得到各自单元的频率-频率多站数据矩阵(Individual-FF-MDM),大小为S×P,其中S是粗频采样点的数量,P是细频采样点的数量. 沿着列方向堆砌所有的Individual-FF-MDM形成一个新的大小为(N×S)×P的矩阵,其中N是接收单元的数量,我们称之为全体频率-频率多站数据矩阵(Full-FF-MDM).

在对Full-FF-MDM进行奇异值分解获得耦合了目标位置信息的左奇异值向量后,我们利用一种新的时间反转成像方法来定位目标. 该方法利用来自不同接收单元的回传辐射信号在目标处同时达到波形的最大值来实现定位,称之为基于同步性的时间反转成像(Time Reversal Imaging based on Synchronism, TRIS)方法[19]. 传统上的时间反转成像是通过辐射时间反转信号到成像区域,然后“抓拍”参考时刻“t=0”时成像区域的信号强度分布;然而,参考时刻“t=0”并不总是能精确地知道[18]. TRIS解决了这个问题,它通过一个同步性峰值搜索来自动确定空间聚焦位置和聚焦时刻(参考时间点“t=0”). TRIS方法充分利用了回传辐射信号的最大值在目标位置处具有同步性而在非目标处具有非同步性的特点,可以同时获得良好的横向和纵向分辨率.

1 方法

1.1 Full-FF-MDM的奇异值分解

在这部分,我们引入FF-MDM的奇异值分解. 考虑单发射单元,多接收单元的时间反转结构. 发射单元发射一UWB脉冲信号到探测区域,TRM接收单元记录散射信号. 在第n个接收单元上的记录信号通过细频(ωf)和粗频(ωc)分别采样得到大小为S×P的矩阵,即individual-FF-MDM:

(1)

(2)

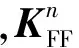
(3)

式中:

qn(rm,ωc)= [G(rn,rm,ω11)s(rm,ω11),…,

G(rn,rm,ωS1)s(rm,ωS1)]T，

(4)

qn(rm,ωf)= [G(rn,rm,ω11)s(rm,ω11),…,

G(rn,rm,ω1P)s(rm,ω1P)]T.

(5)

是大小为S×1和P×1的向量,向量中的元素是背景格林函数和入射信号的乘积;χn(rm)是一个耦合了第m个散射体散射强度的系数.

沿着矩阵的列方向堆砌来自不同接收单元的Individual-FF-MDM,形成一个大小为(N×S)×P的Full-FF-MDM:

(6)

(7)

因此,我们能得到在第n个接收单元上的用于定位第m个目标散射体的时间反转激励脉冲

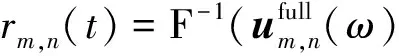
(8)

1.2 基于同步性的时间反转成像(TRIS)

从TRM的第n个接收单元回传辐射式(8)的激励脉冲,则在成像域中的像素点r处的信号是

em,n(r,t)=rm,n(t)⊗tg(r,rn,t),m∈[1,M],

(9)

式中：g(r,rn,t)是从第n个接收单元到像素点r的时域背景格林函数；⊗t表示时域卷积. 根据时间反转原理,式(9)中的[em,1(r,t),…,em,N(r,t)]将在第m个目标散射体处空时聚焦,即它们在第m个目标散射体处将同时到达各自波形的最大值,我们可以令这一时刻为t=τ0. 在其它位置,这种同步性是不成立的.

为了使得所有的目标以相同的可见度显示,对em,n(r,t)进行归一化处理:

(10)

(11)

则Um(r,t)在第m个目标位置处的峰值理论上应为1(由于同步性),而在非目标处近似地为零(非同步性)[19],即目标位置可以通过逐点搜索Um(r,t)的最大值来确定,比如在r=rm位置在t=t0(rm)时刻获得最大值. 因此,可定义最终的成像函数为

Im(r)=Um(r,t0(rm)),

(12)

则这个函数可清晰地显示第m个目标.

2 仿真结果

这部分给出两个仿真例子来验证提出方法的成像性能. 我们用时域有限差分法(Finite-Difference Time-Domain,FDTD)计算波在均匀媒质中的传播和散射(在本次仿真例子中暂时使用自由空间). 成像区域被划分为Nx×Ny=70×60个空间网格,每个空间网格的大小是Δx,y=Δs=λc/10,其中λc是工作信号的中心波长. 将提出的方法扩展到更复杂的媒质中原理上来说仅仅需要作背景格林函数的替换. 发射单元发射一调制高斯脉冲,中心频率fc=5 GHz,有效带宽Δf=8 GHz. TRM 由沿着y轴排列的9个单元构成,阵列单元之间的间距为λc/2.

2.1 单目标探测

一个半径为λc/10的理想导体(Perfect Electric Conductor,PEC)目标位于(4λc,0). 首先我们得到这个成像模型的full-FF-MDM,其中假设ωc=280 MHz,ωf=28 MHz;然后对full-FF-MDM进行奇异值分解. 图1(a)显示了TRM的第一个单元上的第一个左奇异值向量(最大奇异值对应的向量)的相位分布,图1(b)显示了TRM的第五个单元上的第一个左奇异值向量的相位分布. 从图1可以看出,左奇异值向量具有线性相位,这也证实了方程(7)的正确,即左奇异值向量类似于从接收单元到目标散射体的背景格林函数. 将所有接收单元上得到的第一个左奇异值向量用上面介绍的TRIS方法进行处理,得到如图2所示的成像图,它显示了良好的横向和纵向分辨率.

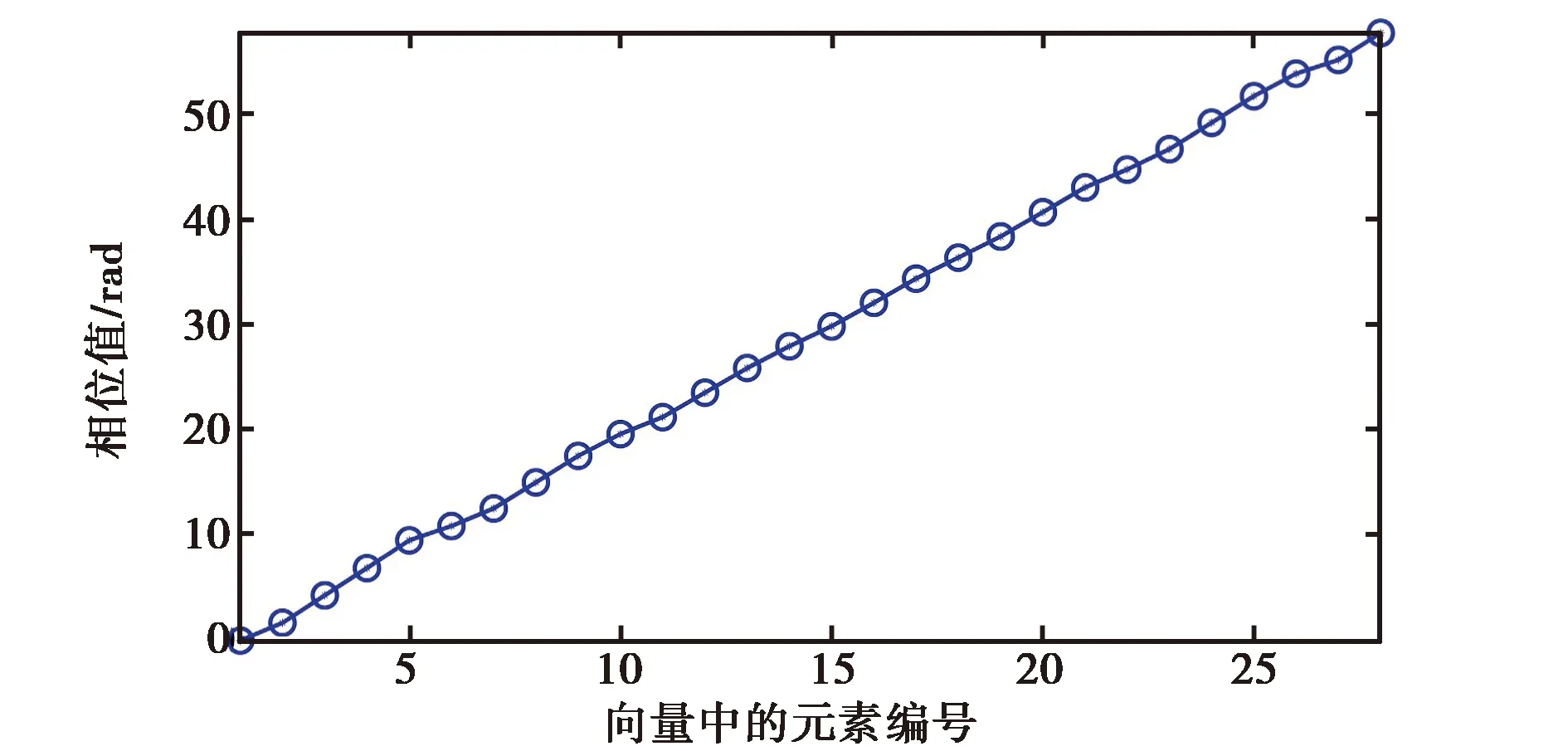
(a) 第一个接收单元上第一个左奇异值向量中各元素的相位分布

(b) 第五个接收单元上第一个左奇异值向量中各元素的相位分布图1 第一个左奇异值向量在第一个和第五个接收单元上的相位分布

图2 利用提出的时间反转成像方法在单个点目标探测情况下的成像结果,图中白色的圆圈表示目标的真实位置

2.2 多目标探测

接下来,我们分析多目标情况下的成像. 考虑两个相同的目标,它们的半径为λc/10,分别位于 (4λc,λc)和(6λc,-λc). 仍然假设ωc=280 MHz,ωf=28 MHz. 图3(a)显示了TRM的第一个单元上的第一个左奇异值向量的相位分布,图3(b)显示了TRM的第一个单元上的第二个左奇异值向量的相位分布. 在图3(b)中,左奇异值向量的线性相位特性稍微被破坏,这可能因为这个向量中也包含了微弱的第一个奇异值对应的目标散射体的信号. 把第一个左奇异值向量应用TRIS法进行处理,得到第一个目标的成像图如图4(a); 类似地,把第二个左奇异值向量用TRIS法进行处理,得到第二个目标的成像图如图4(b).

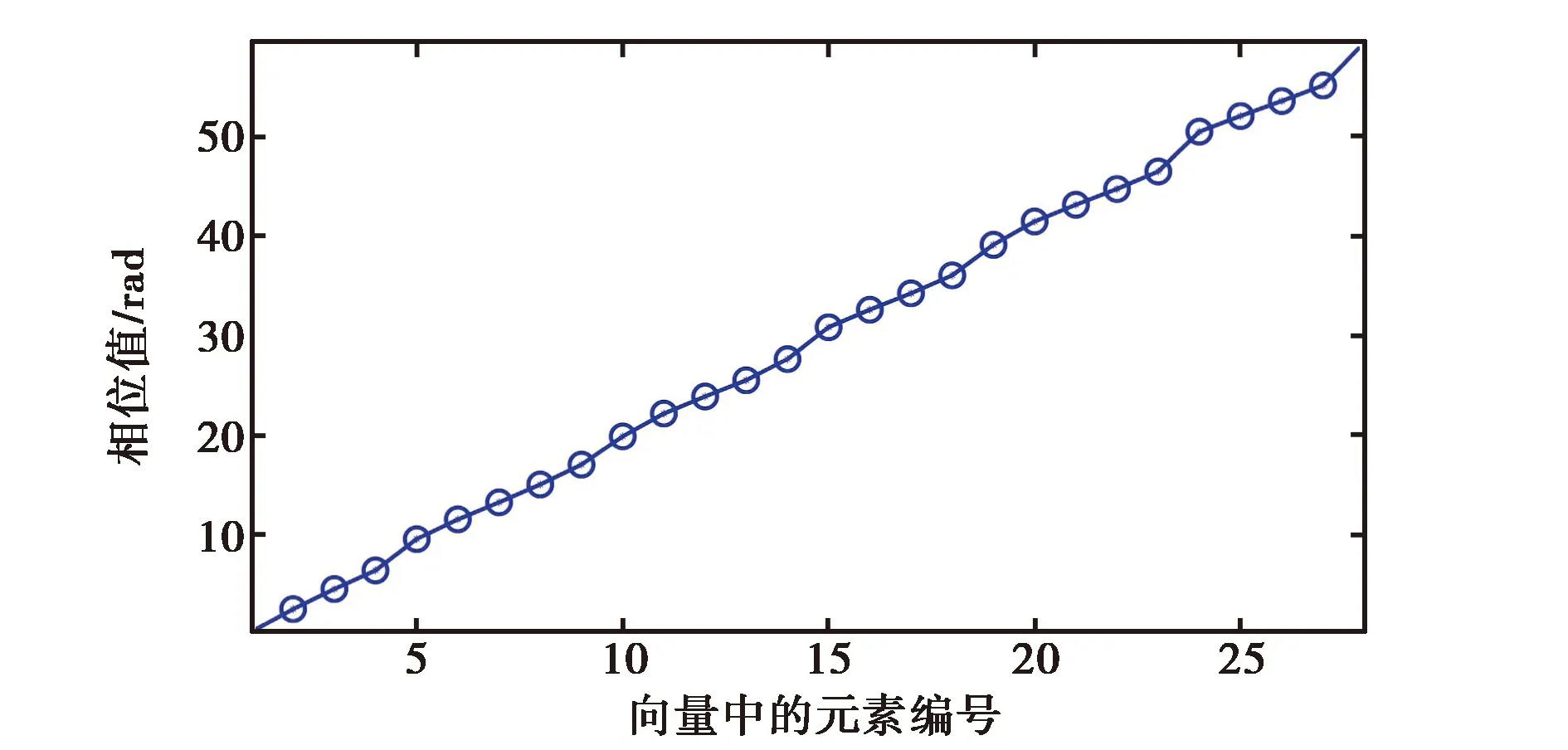
(a) 第一个接收单元上第一个左奇异值向量中各元素的相位分布

(b) 第一个接收单元上第二个左奇异值向量中各元素的相位分布图3 第一个接收单元上第一和第二个左奇异向量的相位分布

(a) 第一个目标的成像图

(b) 第二个目标的成像图图4 利用提出的时间反转成像方法在两个点目标探测情况下的成像结果(图中白色的圆圈表示目标的真实位置)

2.3 算法对比

接下来,我们就成像质量和算法复杂性,与目前两种主要的以时间反转算子分析为基础的时间反转成像方法进行对比,它们是DORT和SF-DORT法.至于TR-MUSIC，在本文的时间反转模型中(单发射单元-多接收单元)不适用,因为不满足发射单元数量不得少于目标数量的要求.

本例中的模型参数设置和小节2.1中的相同. 我们分别应用DORT和SF-DORT进行成像,得到图5(a)和图5(b)的结果,并与本文方法的成像结果图5(c)进行对比. 可以看出,本文方法的分辨率最高,DORT方法次之,SF-DORT的更差一些. 对于算法的计算时间,因为本文方法的第二步完全在时域中进行,而另两种方法仍是在频域中进行,对于超宽带成像来说,时域算法肯定比频域算法效率更高. 具体地,对本算例来说,在同一台微机上运行,本文方法是36s,SF-DORT方法是38s,DORT方法是43s,虽然差别不大,但是优势毕竟存在,这种优势会随着TRM阵列单元数目的增多而更加明显.

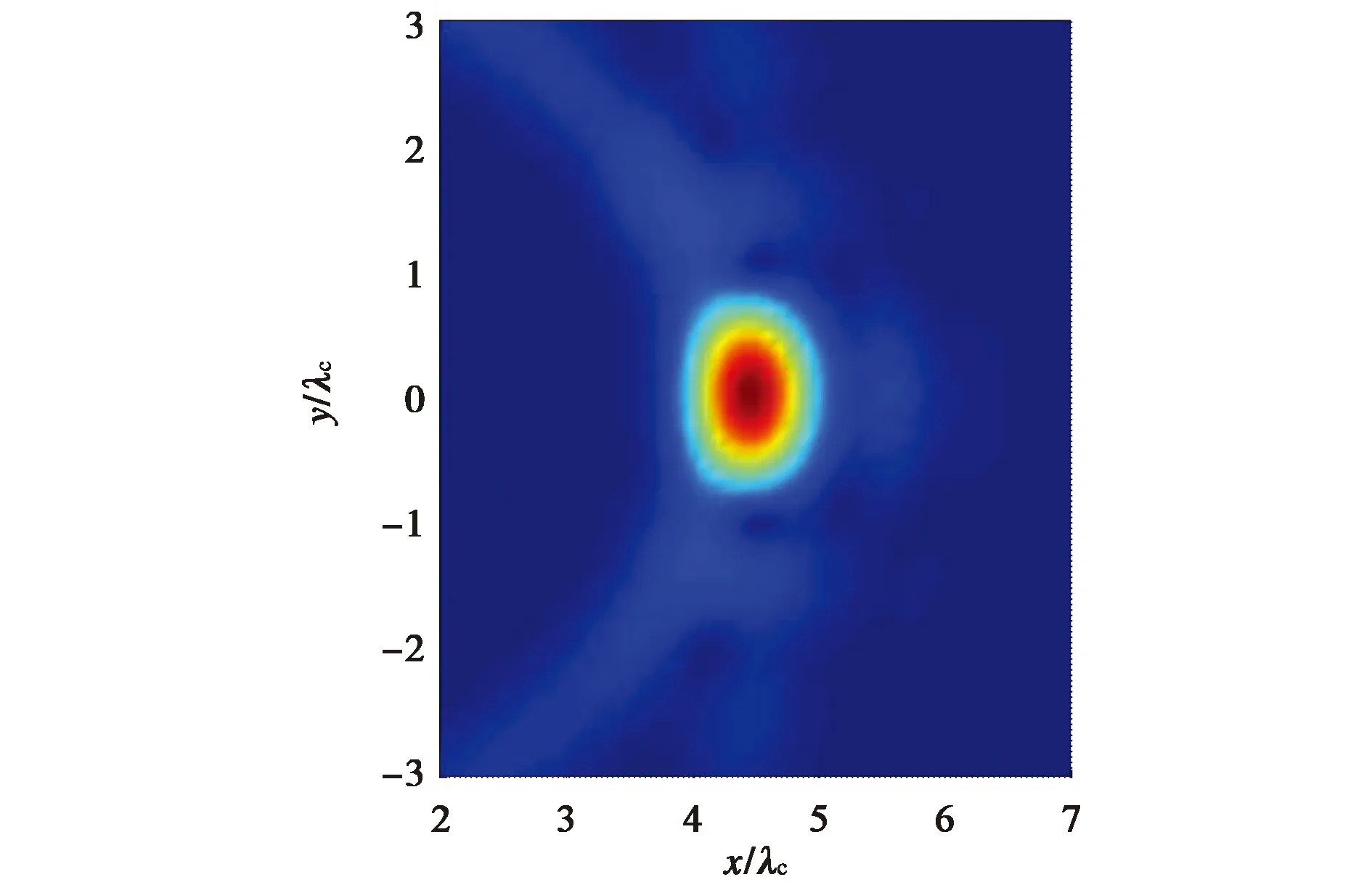
(a) DORT方法

(b) SF-DORT方法

(c) 本文基于频域数据采样和时域信号同步的TR成像法图5 分别利用DORT、SF-DORT和本文方法对位于(4λc,0)的点目标进行成像的结果

3 结 论

本文提出了一种新的TR成像方法,它基于Full-FF-MDM的奇异值分解和TRIS算法的结合. 通过两个仿真例子(单目标和多目标),验证了所提出方法的性能. 该方法无论对单目标还是多目标都只需要一个发射单元,成像质量和计算复杂度与目前同类的TR成像方法相比具有一定的优势.

[1]FINKM,CASSEREAUD,DERODEA,etal.Time-reversedacoustics[J].Reportsonprogressinphysics, 2000, 63(12): 1933-1995.

[2]DEROSNYJ,LEROSEYG,TOURINA,etal.Timereversalofelectromagneticwaves[J].PhysicalReviewLetters, 2004, 92(19): 193904.

[3]YAVUZME,TEIXEIRAFL.Ultra-widebandmicrowavesensingandimagingusingtime-reversaltechniques:areview[J].Remotesensing, 2009, 1: 466-495.

[4] 陈秋菊, 姜秋喜, 曾芳玲, 等. 稀疏阵列时间反演脉冲信号空间功率合成方法[J]. 电波科学学报, 2016, 31(3): 553-561.

CHENQJ,JIANGQX,ZENGFL,etal.Spatialpowercombiningoftime-reversedpulseusingsparsearray[J].Chinesejournalofradioscience, 2016, 31(3): 553-561. (inChinese)

[5]NGUYENHT,ANDERSENJB,PEDERSENGF,etal.Timereversalinwirelesscommunications:Ameasurement-basedinvestigation[J].IEEEtransactionsonwirelesscommunity, 2006, 5(8): 2242-2252.

[6]KUML,HANY,LAIHQ,etal.Powerwaveforming:wirelesspowertransferbeyondtimereversal[J].IEEEtransactionsonsignalprocessing, 2016, 64(22): 5819-5834.

[7]LIUXF,WANGBZ,XIAOSQ.Electromagneticsubsurfacedetectionusingsubspacesignalprocessingandhalf-spacedyadicGreen'sfunction[J].Progressinelectromagneticsresearch-PIER, 2009, 98: 315-331.

[8]LIL,ZHANGW,LIF.Anovelautofocusingapproachforreal-timethrough-wallimagingunderunknownwallcharacteristics[J].IEEEtransactionsongeoscienceremotesensing, 2010, 48(1): 423-431.

[9]KOSMASP,RAPPAPORTCM.TimereversalwiththeFDTDmethodformicrowavebreastcancerdetection[J].IEEEtransactionsonmicrowavetheorytechnology, 2005, 53(7): 2317-2323.

[10]PRADAC,MANNEVILES,SPOLIANSKYD,etal.Decompositionofthetimereversaloperator:Detectionandselectivefocusingontwoscatterers[J].JournaloftheacousticalsocietyofAmerica, 1996, 99(4): 2067-2076.

[11]DEVANEYAJ.Super-resolutionprocessingofmulti-staticdatausingtimereversalandMUSIC[EB/OL]. [2017-02-25].http://www.ece.neu.edu/fac-ece/devaney/ajd/preprints.htm.

[12]YAVUZME,TEIXEIRAFL.Fulltime-domainDORTforultrawidebandfieldsindispersive,randominhomogeneousmedia[J].IEEEtransactionsonantennaspropagation, 2006, 54(8): 2305-2315.

[13]YAVUZME,TEIXEIRAFL.Space-frequencyultrawidebandtime-reversalimaging[J].IEEEtransactionsongeoscienceandremotesensing, 2008, 46(4): 1115-1124.

[14] 钟选明, 廖成, 冯菊. 基于空谱分解的时间反演时域成像[J]. 电波科学学报, 2014, 29(3): 476-479.

ZHONGXM,LIAOC,FENGJ.Time-reversaltime-domainimagingalgorithmbasedonspace-frequencydecomposition[J].Chinesejournalofradioscience, 2014, 29(3): 476-479. (inChinese)

[15]BAHRAMIS,CHELDAVIA,ABDOLALIA.Ultrawidebandtime-reversalimagingwithfrequencydomainsampling[J].IEEEtransactionsongeoscienceandremotesensing, 2014, 11(3): 597-601.

[16]SAKAMOTOT,SATOT.Time-reversalUWBimagingwithasingleantennainmulti-pathenvironment[C]//Proceedingof3rdEuCAP, 2009: 2177-2181.

[17]SAKAMOTOT,SATOT.Imagingsharpeningwithwaveformcompensationforthefrequency-domainDORTwithasingleantennaUWBradar[C]//IEEEInternationalSymposiumonAntennasandPropogation,2011:484-487.

[18]FOUDAAE,TEIXEIRAFL.Statisticalstabilityofultrawidebandtime-reversalimaginginrandommedia[J].IEEEtransactionsongeoscienceandremotesensing,2014, 52(2): 870-879.

[19]LIYQ,XIAMY.Targetlocationbasedontimefocusingoftime-reversalretransmittingsignals[C]//IEEEInternationalSymposiumongeoscienceandremotesensing,2015: 3149-3151.

李元奇 (1983—),男,四川人,电子科技大学博士研究生,研究方向:目标电磁探测与成像.

夏明耀 (1963—),男,江西人,北京大学教授,博士生导师,研究方向:计算电磁学与应用、目标电磁探测与成像、微带电路与天线、微波散射遥感建模.

Time reversal imaging based on frequency domain sampling and time domain synchronism

LI Yuanqi1XIA Mingyao2

(1.UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,China;2.PekingUniversity,Beijing100871,China)

An ultrawideband (UWB) time-reversal (TR) imaging method based on frequency domain sampling and time domain synchronism is presented. A pulse signal from a single transmitter is sent to the imaging domain, and the scattering fields are received by each element of the time-reversal mirror (TRM). A multistatic data matrix (MDM) at each element is formed by casting the fine and coarse frequency domain samples of the scattering information into a matrix form, called findividual requency-frequency MDM(FF-MDM). A full FF-MDM is constructed by stacking all the individual FF-MDM together, and the singular value decomposition (SVD) is applied to the full FF-MDM. The left singular vectors provide the spatial information for focusing the embedded targets or scatter centers, and different left singular vectors correspond to different targets. Each left singular vector at each TRM element is converted into the retransmitting pulse signal, and these retransmitted signals from each TRM element will achieve their waveform maximum values synchronically at the corresponding target position but non-synchronically at other positions. As a result, by defining the multiplication of these retransmitted signals as the final imaging function, good resolutions in both down-range and cross-range directions can be obtained.

frequency domain sampling; singular value decomposition; time-reversal imaging; time domain synchronism

2017-02-05

国家自然科学基金 (61531001，61271032)

10.13443/j.cjors.2017020501

TN820

A

1005-0388(2017)01-0001-07

联系人： 夏明耀 E-mail: myxia@pku.edu.cn

李元奇,夏明耀. 基于频域数据采样和时域信号同步的超宽带时间反转成像[J]. 电波科学学报,2017,32(1):1-7.

LI Y Q, XIA M Y. Time reversal imaging based on frequency domain sampling and time domain synchronism [J]. Chinese Journal of Radio Science,2017,32(1):1-7. (in Chinese). DOI: 10.13443/j.cjors.2017020501