风轮机雷达散射特性仿真及微多普勒特征分析
2017-05-19何炜琨石玉洛郭双双王晓亮吴仁彪
何炜琨 石玉洛 郭双双 王晓亮 吴仁彪
(中国民航大学天津市智能信号与图像处理重点实验室,天津 300300)
风轮机雷达散射特性仿真及微多普勒特征分析
何炜琨 石玉洛 郭双双 王晓亮 吴仁彪
(中国民航大学天津市智能信号与图像处理重点实验室,天津 300300)
风轮机复杂的电磁散射特性,会对其附近的空管通信、导航和监视等电子设备产生严重影响.研究风轮机的电磁散射特性,可为风轮机杂波检测和抑制提供理论依据,对保证空中交通安全具有重要的意义.论文首先基于风轮机散射点叠加的理论,考虑了雷达入射波到风轮机叶片和桅杆的初始相位以及入射波方位角和俯仰角对回波的影响,将单基地回波模型扩展到双基地模型.同时,在散射点叠加模型的基础上,提出了基于混合模型的风轮机散射特性分析.混合模型结合了散射点叠加模型和电磁仿真软件FEKO的优点,考虑了电磁波在叶片和桅杆上的反射系数等因素对回波的影响,可以实现任意观测点处的电磁散射特性计算及其微多普勒特征的分析.最后,分别对散射点叠加模型、FEKO以及混合模型的风轮机电磁散射特性分析方法进行了对比分析,给出了各自的优缺点及其适用场合.
风轮机;混合模型;雷达散射特性;微多普勒特征
DOI 10.13443/j.cjors.2016030402
引 言
作为清洁能源的一种形式,风力发电目前在全世界受到了高度关注,近年来我国风力发电装机容量也呈现指数增长态势.研究表明,由于其复杂的电磁散射特性,风轮机会对其附近的通信、导航和监视等设备产生严重影响,威胁民航飞行安全[1-9].风轮机高度(包括叶片)能达到100多米,导致风轮机的雷达散射截面积(Radar Cross Section,RCS)可以和波音747的RCS相比拟,会引起雷达接收机饱和;风电场往往成片地分布数台甚至上百台风轮机,会对电磁波传播有明显遮挡;同时,由于风轮机的叶片是运动的,且叶片不同部分的转动线速度不同,故风轮机会对雷达回波信号产生多普勒影响,引起误检测和误跟踪.研究风轮机的雷达散射特性及其微多普勒特征是检测与抑制风电场干扰的基础,具有十分重要的意义.
分析风轮机的雷达散射特性,通常先建立风轮机的RCS模型.目前国内外学者已做了大量研究,VictorC.Chen和冯孝斌等人[10-12]基于散射点叠加理论研究了旋翼螺旋桨飞机的雷达电磁散射特性及其频谱特征.吴仁彪和Rashid L S等人[13-15]在此基础上,建立了风轮机回波的散射点叠加模型,能简单仿真风轮机雷达回波信号的某些特性,但其不能实现任意观测点处(不同方位角、俯仰角)的风轮机回波仿真.何炜琨等人[16]在散射点叠加模型的基础上,考虑了分风轮机之间以及风轮机与地面之间的多径散射,建立了风电场多径散射模型,实现了风电场的回波仿真.但上述方法均没有考虑电磁波在风轮机叶片及桅杆的电磁散射特性(反射系数等参数)对回波的影响,准确度不高.Kent B M、Lok Y F和Ohs R R等人[17-19]利用电磁仿真软件计算风轮机的RCS,如X-Patch、XGtd等.基于电磁软件的RCS分析方法需要首先建立风轮机三维模型,然后利用软件自带的电磁仿真算法计算和分析风轮机的RCS,其复杂度和运算量均较高,且受到信号频率的限制.Kong Fan-xing和Zhang Yan等人[21-22]利用按比例缩小的风轮机计算机模型和实验室模型,通过比较风轮机RCS的计算机仿真结果和微波暗室测量结果,预测完整风轮机的电磁散射特性,但此方法风轮机模型制作困难,不方便修改相关参数,且操作复杂、成本高.
本文在传统散射点叠加理论的基础上,考虑了雷达入射波到风轮机叶片和桅杆的初始相位以及入射波方位角和俯仰角对回波的影响,将单基地回波模型扩展到了双基地模型,研究了风轮机电磁散射特性的仿真问题.同时,结合散射点叠加模型及电磁仿真计算软件FEKO的优点,提出了基于混合模型的风轮机电磁散射特性仿真,该模型考虑了电磁波在叶片及桅杆上的反射系数等因素对回波的影响,实现了任意观测点处的风轮机雷达散射特性仿真及其微多普勒特征分析.最后,分别对散射点叠加模型、FEKO以及混合模型的风轮机电磁散射特性分析方法进行了对比分析,给出了各自的优缺点及其适用场合.
1 基于散射点叠加模型的风轮机散射特性分析
发射信号波长远小于目标尺寸时,目标可近似为一组离散的散射体的集合,相应地,雷达发射信号被目标散射体延时和幅度调制后形成散射体子回波,来自目标的后向散射信号可认为是各散射体子回波的矢量和,这就是雷达目标的散射点叠加模型假设.现有空管雷达发射信号的波长远小于风轮机尺寸,因此,可以利用目标散射点叠加理论建立风轮机回波信号数学模型.本文在仿真与分析中,均采用目标散射点叠加模型假设,将风轮机叶片和桅杆等效为细长的圆柱体,并将圆柱体沿轴向分割成一系列薄圆片,风轮机回波可近似为一系列薄圆片中心点回波的合成,如图1所示.

图1 风轮机散射点几何模型
1.1 单基地雷达风轮机散射特性分析
风电场的主体是风轮机,风轮机一般由桅杆、轮机舱和旋转叶片三部分组成,各部分的电磁波散射特征不同.其中桅杆和轮机舱是静止的,对雷达波有较强散射,等效为具有一定的RCS、零多普勒频率的静止目标.叶片则不停转动,表现出运动目标的特征,由于叶片不同部分的转动线速度不同,故其雷达回波信号具有很宽的多普勒谱.
由于桅杆和轮机舱属于静止目标,其回波易于分析和计算,故主要介绍旋转目标叶片的回波模型.单基地模型风轮机叶片与雷达的几何关系如图2所示.雷达波束相对于风轮机的方位角α定义为雷达视线(Line of Sight,LOS)在XOY面内的投影与X轴正方向夹角,俯仰角β定义为雷达LOS与Z轴正方向的夹角.P是旋转叶片上的任一点,它到叶片轴心O的距离为li,以转速frot绕叶片轴心O旋转.雷达与风轮机叶片轴心之间的距离为r,雷达LOS与叶片夹角为φ(t),波束直接照射风轮机叶片轴心.
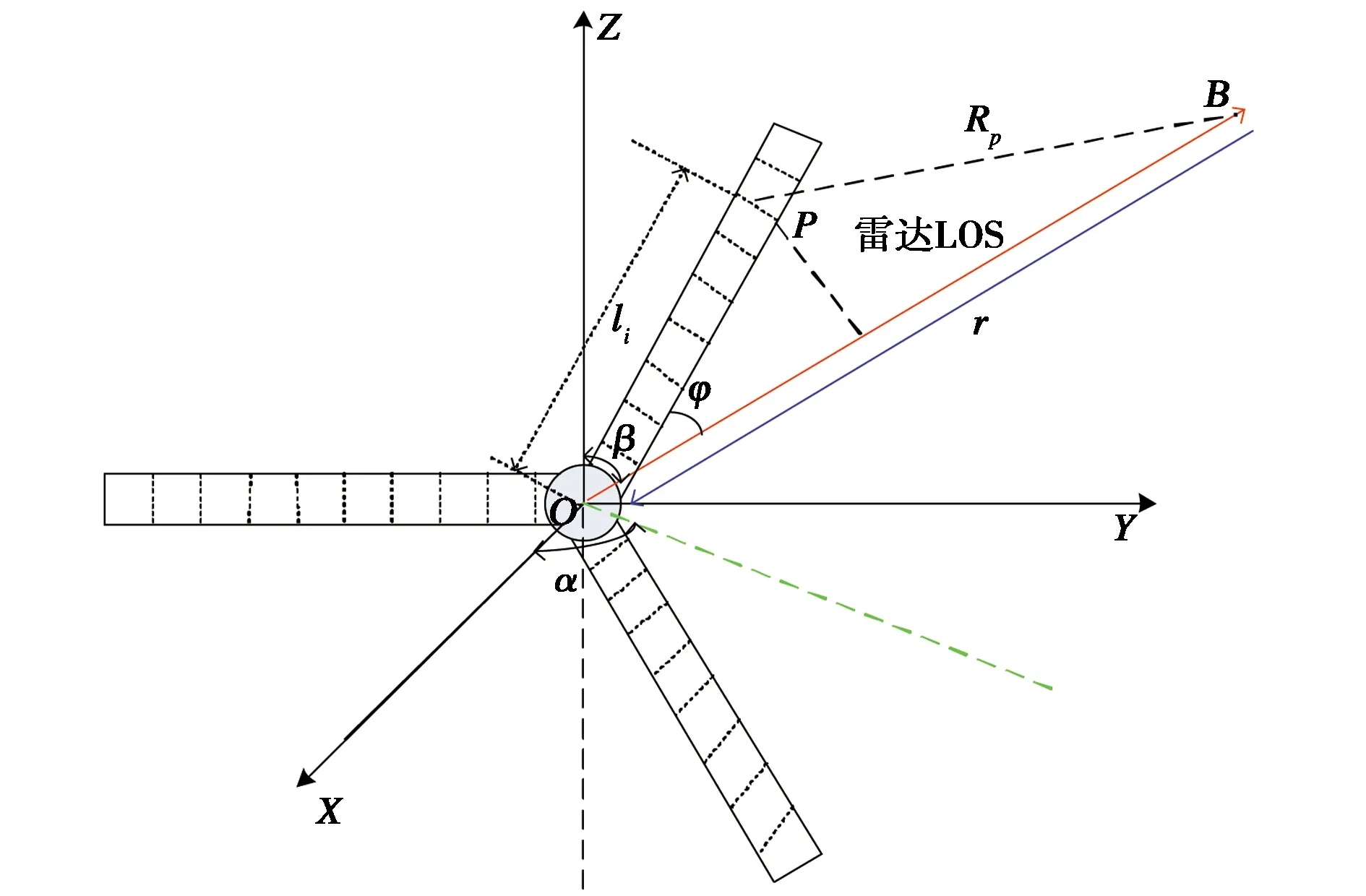
图2 单基地模型风轮机叶片与雷达位置关系
叶片上任一点P到雷达的距离为RP(t),由于(li/r)2→0,故
≈r-licosφ(t) .
(1)
则雷达接收到的P点的回波信号为
(2)
式中,fc和λ分别为发射信号的中心频率和波长.去掉载波和恒定相位项,可得基带信号
(3)
在叶片的长度L上对式(3)积分,得到整个叶片的回波信号为
(4)
由于风轮机由N个叶片组成,与雷达LOS相应的夹角分别为φ1(t),φ2(t),…,φN(t),于是所有叶片总的回波信号为
(5)
式中,φk(t)为第k个叶片与雷达LOS的夹角,根据风轮机与雷达视线的相对位置关系及立体几何中的相关知识,经过推导可知,cosφk(t)=cosθk(t)
sinαsinβ+sinθk(t)cosβ,θk(t)为t时刻第k个叶片与Y轴正方向的夹角.
桅杆和轮机舱可等效为静止目标,轮机舱的回波较小,忽略不计.基于散射点叠加模型,桅杆的回波信号可以写为
(6)
式中,M为桅杆高度.因此风轮机回波可表示为
sWT(t)=sBlade(t)+sMast(t).
(7)
单基地回波模型中,没有考虑雷达入射波到风轮机叶片和桅杆的初始相位以及入射波方位角和俯仰角对回波的影响.为提高回波模型的普适性,需要将单基地模型扩展到双基地,进一步分析双基地风轮机雷达回波仿真问题.
1.2 双基地雷达风轮机散射特性分析
所谓双基地回波模型是指雷达的发射机和接收机在不同的位置.双基地模型风轮机叶片与雷达的几何关系如图3所示.雷达波束相对于风轮机的方位角与俯仰角的定义与单基地模型类似,其中,αi和βi分别表示入射波的方位角和俯仰角,αs和βs分别表示反射波的方位角和俯仰角.雷达入射波到风轮机叶片轴心之间的距离为r1,风轮机叶片轴心到观测点之间的距离为r2.雷达入射波与叶片夹角为φi(t),反射波与叶片夹角为φs(t).波束直接照射风轮机叶片轴心.

图3 双基地模型风轮机叶片与雷达位置关系图
如上所述,雷达入射波到叶片上任一点P的距离为RP(t),则
≈r1-licosφi(t).
(8)

≈r2-licosφs(t) .
(9)
观测点接收到的反射回波信号为
(10)
去掉载波和恒定相位项,可得
(11)
则整个叶片的回波为
(12)
由于风轮机由N个叶片组成,第k个叶片与发射波束和反射波束的夹角分别为φki(t),φks(t),于是风轮机叶片总的回波信号为
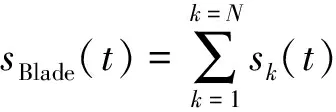
(13)
轮机舱的回波较小,忽略不计.桅杆的回波信号为
(14)
因此,风轮机回波可表示为
sWT(t)=sBlade(t)+sMast(t).
(15)
综上所述,散射点叠加模型是从雷达信号传输的数学模型出发,没有考虑电磁波在叶片及桅杆上的反射系数等因素的影响,因而其精度在一定程度上会受影响.
FEKO是美国ANSYS公司推出的一款针对天线设计、电磁兼容性分析与目标RCS分析的一款强大的三维全波电磁仿真软件.FEKO以矩量法(Method of Moments,MoM)为基础,采用多层快速多极子方法(Multilevel Fast Multipole Algorithm,MLFMA),并与物理光学 (Physical Optics,PO) 法、一致性几何绕射理论(Uniform Theory of Diffraction,UTD)等高频分析方法相结合,分析各种电磁辐射、散射、电磁兼容性(Electro Magnetic Compatibility,EMC)等确定性问题,在世界范围内得到了广泛的应用.FEKO在计算风轮机等电大尺寸目标的RCS过程中具有较大的优势,能够较好地解决风轮机RCS精确计算问题.但由于风轮机属于电大尺寸目标,对于一般常用的个人计算机,其计算时间仍较长、占用计算资源较大.同时,为进一步揭示风轮机回波信号特征,往往需要进行风轮机回波信号的微动特征分析与提取,而FEKO实现这方面的分析却很困难.
2 基于混合模型的风轮机散射特性分析
如上所述,FEKO软件可以较为准确地仿真风轮机RCS,但为突出风轮机回波信号特征,为风电场杂波检测和抑制提供理论依据,往往需要进行风轮机回波信号的微动特征分析,进而需要提取风电场杂波时域、频域以及时频域等微多普勒特征,而FEKO实现这方面的分析却较为困难.风轮机回波信号的散射点叠加模型可以快速、方便地仿真风轮机回波信号,并能够对回波信号进行微多普勒特征分析,但其准确性较差.混合模型结合风轮机回波信号的散射点叠加模型和基于FEKO的风轮机RCS特性,能够较为准确地仿真风轮机雷达回波信号,并能够方便地进行时域、频域与时频域等方面的微动特性分析,其具体步骤如下:
步骤1:利用FEKO软件,在不同的场景下计算风轮机的RCS(σ),包括不同方位角和俯仰角、叶片旋转到不同位置的RCS(σ),将结果存入数据表中.
步骤2:按照一定的比例对σ进行插值,得到叶片在所需位置的RCS.
步骤3:从步骤2计算的风轮机RCS数据表中查找当前仿真场景对应的风轮机各部分的RCS,作为散射系数代入风轮机回波的散射点叠加模型中.
步骤4:利用混合模型得到风轮机回波信号,对其进行后处理,分析风轮机的雷达散射特性及其微多普勒特征.
基于混合模型的风轮机叶片及桅杆的回波信号可以写为:
(16)
(17)
式中:σk(t)是t时刻第k个叶片的RCS;σ是桅杆的RCS,将式(16)~(17)代入式(15)即可以实现风轮机雷达回波的散射特性分析.
3 风轮机RCS仿真与分析
RCS是评价目标对电磁波散射能力的一个通用电磁参数,是一个电磁波频率、三维空间坐标,以及时间的复杂函数,其函数关系较为复杂,一般用符号σ表示.在远场条件下,RCS可写为

(18)
式中:Ei、Hi分别为目标处入射波的电场和磁场强度;Es、Hs分别为观测点处的电场和磁场强度.
RCS既与目标的形状、尺寸、结构及材料有关,也与入射电磁波的频率、极化方式和入射角等有关.分别基于风轮机回波信号的散射点叠加模型,FEKO软件和混合模型,仿真并分析了风轮机的RCS特征.为了便于与文献结果[23]进行对比分析,将发射信号频率设置为810 MHz,考虑垂直照射的情况,即雷达入射波的方位角αi为0°,俯仰角βi为90°.仿真实验中相关参数如表1及表2所示.风轮机叶片的RCS随方位角和俯仰角变化的仿真结果如图4~7所示.
图7是西班牙巴斯克大学的AnguloI和DeLaVegaD等人仿真的结果[23],是利用在MATLAB环境中基于PO方法开发的PO-Facets工具所仿真的,具有一定的广泛性和代表性.从图4~7可以得出以下结论:1)风轮机叶片的RCS是观测点俯仰角或方位角的函数(0°≤βs≤180°,0°≤αs≤360°).风轮机的RCS随方位角变化缓慢,在观测点方位角为0°和180°时,RCS出现峰值,分别对应后向散射前向散射.当观测点俯仰角βs在90°附近时,RCS发生剧烈变化,且当βs=90°时RCS最大,此时发射波束在风轮机叶片上相当于发生了镜面反射. 2)散射点叠加模型没有考虑叶片的反射系数和复杂的电磁散射等因素的影响,因而仿真结果在数值上与其他仿真结果有较大差别.3) FEKO和 PO-Facets的仿真结果更接近,因为它们都是基于高频电磁计算方法——PO法计算所得.但也存在着一定的差别,这主要是由于仿真时风轮机叶片的具体形状不同(PO-Facets 仿真时采用的是精确的叶片模型,而FEKO采用的却是简化模型)以及仿真时两种仿真工具内部参数(如网格划分等参数)设置不一致造成的. 4)混合模型加入了叶片的散射系数,与散射点叠加模型相比,仿真结果更接近PO-Facets的仿真结果.

表1 雷达参数

表2 风轮机参数

(a) RCS随方位角变化 (b) RCS随俯仰角变化图4 散射点叠加模型(双基地)仿真结果

(a) RCS随方位角变化 (b) RCS随俯仰角变化图5 FEKO仿真结果

(a) RCS随方位角变化 (b) RCS随俯仰角变化图6 混合模型仿真结果

(a) RCS随方位角变化 (b) RCS随俯仰角变化图7 POFacets工具仿真结果[23]
桅杆的RCS随方位角和俯仰角变化的仿真结果如图8~11所示.从图8~11可以看到:1)与叶片类似,当观测点俯仰角βs在90°附近时,桅杆的RCS发生剧烈变化.对于散射点叠加模型,βs=90°时RCS最大,然而,FEKO、混合模型和PO-Facets工具仿真结果中RCS却是在βs=89°时出现最大值,这是因为桅杆是圆台模型,而散射点叠加模型无法区分圆柱与圆台模型.2)当观测点方位角变化时,对于散射点叠加模型,桅杆RCS不变.3)混合模型与散射点叠加模型相比,结果更接近FEKO和PO-Facets工具仿真结果.4)FEKO和PO-Facets工具仿真结果基本一致.

(a) RCS随方位角变化 (b) RCS随俯仰角变化图8 散射点叠加模型(双基地)仿真结果

(a) RCS随方位角变化 (b) RCS随俯仰角变化图9 FEKO仿真结果

(a) RCS随方位角变化 (b) RCS随俯仰角变化图10 混合模型仿真结果
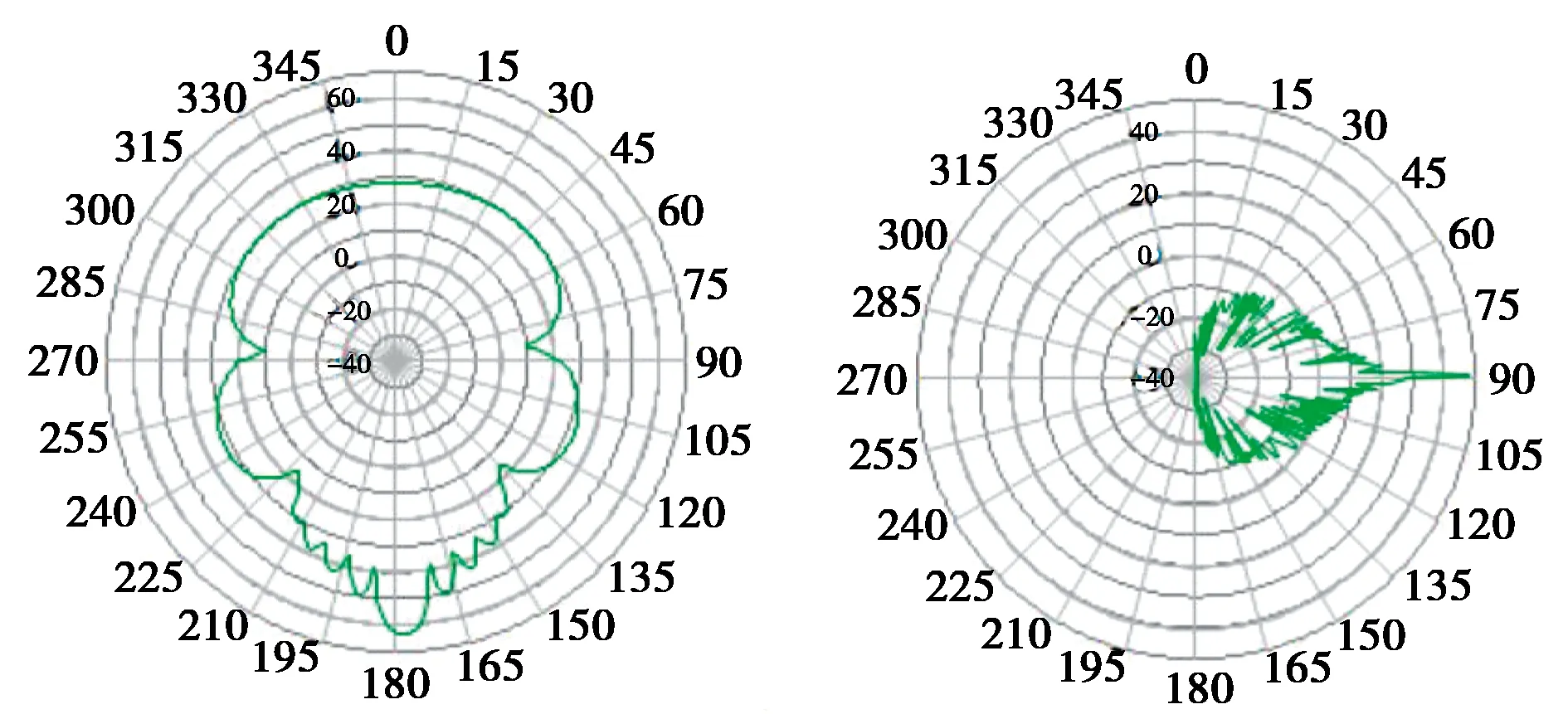
(a) RCS随方位角变化 (b) RCS随俯仰角变化图11 PO-Facets工具仿真结果
图12表示在任意观测点处风轮机的RCS.从图12可以看到,在不同观测点处,风轮机RCS不同,其变化范围较大.

图12 风轮机RCS随观测点俯仰角和方位角变化结果
需要说明的是,本文的仿真都是在一般的个人计算机上操作的.计算机型号为联想启天M690E,CPU型号为Inter奔腾双核E5300,CPU频率2.60 GHz,内存2 GB,所使用的仿真软件为MATLAB R2010a和FEKO 6.0.对于特定风电场,混合模型首先将不同场景下(包括不同方位角、俯仰角、叶片旋转到不同位置等)的风电场散射系数预存到一个数据表中,且对于该风电场的后续数据处理(包括风电场杂波检测、抑制等)均可查找该数据表获得其对应的散射系数,代入混合模型中即可得到雷达回波信号.在预先计算出散射系数的前提下,混合模型的运算时间在数秒之内.相比较而言,对于某一特定风电场的不同的场景及其后续的数据处理,FEKO均需重新进行三维建模、物理剖分、数值计算等,需要几十个小时才能完成(具体时间与信号频率及网格划分直接相关).
4 风轮机回波信号微多普勒分析
风轮机的雷达回波主要由叶片回波、桅杆回波和轮机舱回波组成.桅杆和轮机舱属于风轮机静止部分,其回波与一般的地杂波类似;叶片由于不停地旋转,其回波存在多普勒频移.这里采用短时傅里叶变换(Short-Time Fourier Transform,STFT)对回波信号进行微多普勒分析,仿真参数如表1和表2所示.结果如图13所示.

(a) 散射点叠加模型仿真结果

(b) 混合模型仿真结果

(c) 实测数据结果图13 风轮机回波信号微多普勒分析
从图13可知:1)风轮机回波出现了多普勒频率闪烁的现象,闪烁出现的周期是叶片转速和叶片个数的函数.零多普勒频率对应的是风轮机静止部分(桅杆)的回波.这是因为:在叶片旋转面内,当叶片与雷达LOS垂直时,叶片上所有散射点回波具有相同的相位,叠加后幅度增加,能量急剧上升;当叶片与雷达LOS不垂直时,叶片上各散射点回波的相位不一样,叠加后部分相消,能量下降.2)三个叶片的叶尖相当于做圆周运动,图13(a)中三组能量微弱的正弦形状的多普勒频率对应的是叶片叶尖散射点回波,图13(b)是混合模型仿真结果,加入了散射系数,正弦形状的多普勒频率被淹没了.3)图13(c)是实测数据[2],定性地比较图13(a)、(b)、(c)可知,仿真数据与实测数据所反映的信号特性基本一致,其中混合模型考虑了叶片上每个散射点的散射系数,更接近于实测数据结果.
风轮机多普勒频移与发射信号波长、叶片旋转速度、叶片长度、叶片旋转面和雷达波束夹角直接相关.根据仿真参数,可计算出叶片叶尖的线速度v为

(19)
叶片旋转过程中产生的最大多普勒频率fd max为

(20)
从图13(a)、(b)可看出,仿真结果与理论分析一致.因此,由风轮机回波信号的微多普特征,可以估计出风轮机叶片的旋转周期、旋转速度等参数,为风轮机参数辩识、风电场杂波检测与抑制提供理论依据.
5 结 论
1) 基于散射点叠加模型的风轮机散射特性分析方法,计算量较小,可用来方便快捷地提取风轮机雷达回波信号特征,但是该模型没有考虑电磁波的复杂散射特性和叶片及桅杆的反射系数等因素的影响,因而其精度较差,可在定性分析风轮机回波信号特征的情况下应用.
2) 电磁仿真软件FEKO能够较为精确地分析风轮机的RCS特性,但是计算时间长、占用计算资源大,适合于风轮机精细模型,不需要实时处理情况下的散射特性分析.
3) 基于混合模型的风轮机雷达散射特性分析方法能够在保证仿真精度的前提下,有效地实现风轮机回波信号微多普勒特征的分析,适用于高效评估已建风电场电磁散射特性的分析及风电场杂波的特征提取,可为后续风电场杂波检测与抑制提供理论依据和数据来源.
[1]CARROLLJE,SANDERSFH,TURNERD.Assessmentoftheeffectsofwindturbinesonairtrafficcontrolradars[R].USA:NationalTelecommunications&InformationAdministration,DepartmentofCommerce, 2008: 21-67.
[2] 孙丽梅. 风能利用现状及前景分析[J]. 内蒙古电力 技术, 2010, 28(6): 9-11.
SUNLM.Statusquoofwindpowerutilizationanditsprospectsanalysis[J].InnerMongoliaelectricpower, 2010, 28(6): 9-11. (inChinese)
[3]VOGTRJ,CRUMTD,SANDIFERJB,etal.Awayforward,windfarmWeatherradarcoexistence[R].NOAANEXRADRadarOperationsCenterreport, 2009.
[4]AULDT.Effectsofwindturbinesonradar:apilotstudyofUSconcerns[D].Australian:MurdochUniversity, 2011.
[5]POUPARTGJ.Windfarmimpactonradaraviationinterestfinalreport,DIT/PUB-2003-1294[R].America:DIT, 2003.
[6]MORLAASC,FARESM,SOUNYB.WindturbineeffectsonVORsystemperformance[J].IEEEtransactiononaerospaceandelectronicsystems, 2008, 44(4): 1464-1476.
[7]ANGULOI,DELAVEGAD,CASCNI,etal.Impactanalysisofwindfarmsontelecommunicationservices[J].Renewableandsustainableenergyreviews, 2014, 32(5): 84-99.
[8]THEILA,SCHOUTENMW,DEJONGA.Radarandwindturbines:aguidetoacceptancecriteria[C]//IEEEInternationalRadarConference, 2010: 1355-1361.
[9]BALLERIA,AL-ARMAGHANYA,GRIFFITHSH,etal.MeasurementsandanalysisoftheradarsignatureofanewwindturbinedesignatX-band[J].IETradar,sonar&navigation, 2013, 7(2): 170-177.
[10]CHENVC.Radarsignaturesofrotorblades[J].ProceedingsoftheSPIE, 2001, 4391: 63-70.
[11]冯孝斌, 黄培康.飞机旋转叶片回波频谱特征分析[J].系统工程与电子技术, 2005, 27(3): 285-409.
FENGXB,HUANGPK.Analysisofthespectrumsignatureoftheradarreturnsignalfromaircraftrotatingblade[J].Systemsengineeringandelectronics, 2005, 27(3): 285-409. (inChinese)
[12]蒋相闻, 招启军, 孟晨. 直升机旋翼桨叶外形对雷达特征信号的影响[J]. 航空学报, 2014, 35(11): 3123-3136.
JIANGXW,ZHAOQJ,MENGC.Effectofhelicopterrotorbladeshapeonitsradarsignalcharacteristics[J].Chinesejournalofaeronautics, 2014, 35(11): 3123-3136. (inChinese)
[13]WURB,MAOJ,WANGXL,etal.Simulationofwindfarmradarechoeswithhighfidelity[C]//InternationalConferenceonSignalProcessing.Beijing,October21-25, 2012: 1998-2002.
[14]RASHIDLS,BROWNAK.Impactmodellingofwindfarmsonmarinenavigationalradar[C]//IETInternationalConferenceonRadarSystems, 2007: 1-5.
[15]何炜琨, 石玉洛, 王晓亮, 等. 风轮机雷达回波仿真与分析[J]. 系统仿真学报, 2015, 27(1): 50-56.
HEWK,SHIYL,WANGXL,etal.Simulationandanalysisofwindturbineechoes[J].Journalofsystemsimulation, 2015, 27(1): 50-56.(inChinese)
[16]何炜琨, 郭双双, 王晓亮, 等. 扫描工作模式的航管监视雷达风电场回波信号的微多普勒特征分析[J]. 信号处理, 2015, 31(10): 1240-1246.
HEWK,GUOSS,WANGXL,etal.Micro-Dopplerfeaturesanalysisofwindfarmechoesforairtrafficcontrolradarinscanningmode[J].Signalprocessing, 2015, 31(10):1240-1246.(inChinese)
[17]KENTBM,HILLKC,BUTERBAUGHA,etal.DynamicradarcrosssectionandradarDopplermeasurementsofcommercialgeneralelectricwindmillpowerturbinesPart1:Predictedandmeasuredradarsignatures[J].IEEEantennasandpropagationmagazine, 2008, 50(2): 211-219.
[18]LOKYF,WANGJ,PALEVSKYA.Simulationofradarsignalonwindturbine[C]//IEEERadarConference, 2010: 538-543.
[19]OHSRR,SKIDMOREGJ,BEDROSIANG.Modelingtheeffectsofwindturbinesonradarreturns[C]//MilitaryCommunicationConference, 2010: 272-276.
[20]刘立国, 张国军, 莫锦军, 等. 基于图形电磁学的雷达散射截面计算方法改[J]. 电波科学学报, 2012, 27(16): 1146-1151.
LIULG,ZHANGGJ,MOJJ,etal.Improvementofelectromagneticcomputingmethodforradarcrosssection[J].Chinesejournalofradioscience,2012, 27(16): 1146-1151. (inChinese)
[21]ZHANGY,HUSTONA,PALMERRD,etal.UsingscaledmodelsforwindturbineEMscatteringcharacterization:techniquesandexperiments[J].IEEEtransactiononinstrumentationandmeasurement, 2011, 60(4): 1298-1306.
[22]KONGFX,ZHANGY,PALMERRD.Windturbineradarinterferencestudiesbypolarimetricmeasurementsofascaledmodel[J].IEEEtransactionsonaerospaceandelectronicsystems, 2013, 49(3): 1589-1600.
[23]ANGULOI,DELAVEGAD,RODRGUEZO,etal.AnalysisofthemastcontributiontothescatteringpatternofwindturbinesintheUHFband[C]//Proceedingsofthe5thEuropeanConferenceonAntennasandPropagation, 2011: 707-711.
Simulation on wind turbine radar scattering characteristics and its micro-Doppler analysis
HE Weikun SHI Yuluo GUO Shuangshuang WANG Xiaoliang WU Renbiao
(TianjinKeyLabforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China)
It is shown that wind turbines seriously affect Air Traffic Control (ATC) radars, communication and navigation equipments due to its complex electromagnetic scattering properties. The research on the wind turbine electromagnetic scattering characteristics can provide the theoretical basis for the detection and suppression of wind turbine echo, which is of vital significance for ensuring the air traffic safety. Based on the theory of scattering point superposition, the electromagnetic scattering characteristics of the wind turbine are analyzed under the condition of considering the effect of initial phase of the incident wave propagated to the blade and mast of wind turbines, and the azimuth angle and elevation angle of the incident wave. The mono-static model is expanded to bi-static model. Meanwhile, analysis of the wind turbine scattering characteristics based on hybrid model is proposed. The hybrid model combines the advantages of scattering point superposition model and FEKO, taking into account the impact of reflection coefficient of the blade and mast on the echoes. Wind turbine scattering characteristics at any observation point and micro-Doppler feature are simulated by using of scattering point superposition model, FEKO and hybrid model respectively. Finally, these methods are compared with each other and the corresponding application conditions are given.
wind turbines; hybrid model; radar scattering characteristics; micro-Doppler characteristics
2016-03-04
国家自然科学基金委员会与中国民航局联合资助项目(U1533110);国家自然科学基金项目(61571442);中央高校基本科研业务费资助项目(3122015D005).
10.13443/j.cjors.2016030402
TN955
A
1005-0388(2017)01-0103-09
何炜琨 (1977-),女,黑龙江人,副教授,博士.主要研究方向:雷达信号处理、风电场杂波检测与抑制.
石玉洛 (1988-),男,河南人,硕士.主要研究方向:风电场回波仿真.
郭双双 (1990-),女,河北人,硕士研究生.主要研究方向:风电场杂波特征提取、风电场杂波检测.
王晓亮 (1982-),男,甘肃人,讲师,博士.主要研究方向:雷达信号处理、图像处理与识别.
吴仁彪 (1966-),男,湖北人,教授,博士生导师,IEEE高级会员,天津市重点学科“通信与信息系统”学科带头人,天津市智能信号与图像处理重点实验室主任,国家杰出青年基金获得者,国家人事部百千万人才工程第一、二层次人选,天津市首批3位特聘教授之一,民航首批特聘专家.研究方向:阵列信号处理、自适应信号处理及其应用.
联系人: 何炜琨 E-mail:hwkcauc@126.com
何炜琨,石玉洛,郭双双,等.风轮机雷达散射特性仿真及微多普勒特征分析[J]. 电波科学学报,2017,32(1):103-111.
HE W K, SHI Y L, GUO S S, et al. Simulation of wind turbine radar scattering characteristics and its micro-doppler Analysis[J]. Chinese journal of radio science,2017,32(1):103-111. (in Chinese). DOI: 10.13443/j.cjors.2016030402
