Symmetry Analysis and Exact Solutions of the 2D Unsteady Incompressible Boundary-Layer Equations∗

2017-05-18ZhongHan韩众andYongChen陈勇

Communications in Theoretical Physics 2017年1期

关键词：陈勇

Zhong Han(韩众)and Yong Chen(陈勇)

Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China(Received September 19,2016)

1 Introduction

Group theoretic methods are useful to study similarity reductions and exact solutions of partial differential equations(PDEs).[1−4]The classical symmetry methods due to Lie have been generalized to the nonclassical case by Bluman and Cole.[5]Generally,an s-parameter subgroup of the full symmetry group of a system of PDEs with n＞s independent variables leads to a family of group invariant solutions.Unfortunately,it is usually not practicable to list all possible group invariant solutions of the system as there exist almost an in fi nite number of subgroups.Therefore,to construct all the inequivalent group invariant solutions is anticipated,or equivalently,to give them a classi fication,which leads to the concept of optimal system.In practical,an optimal system of the Lie algebra is constructed,from which the corresponding optimal systems for group invariant solutions are obtained.The adjoint representation of a Lie group on its Lie algebra is known to Lie and its application in classifying group invariant solutions appears from Ovsiannikov.[2]By using a global matrix for the adjoint transformation,Ovsiannikov demonstrates the construction of a one-dimensional optimal system and sketches the construction of higherdimensional optimal systems.Olver adopts a slightly different and elegant way by taking a table of adjoint operators to simplify a general element from the Lie algebra as much as possible.[3]Following Olver’s method,we have obtained the optimal systems as well as some interesting exact solutions for several important PDEs appeared in hydrodynamics and atmosphere.[6−8]Some other works on optimal systems can also be found in Refs.[9–11].Very recently,a direct algorithm of one-dimensional and twodimensional optimal system is introduced in Refs.[12]and[23],respectively.The algorithm can guarantee both comprehensiveness and inequivalence of the elements in the optimal system obtained,need no further proofs.

As a matter of fact,the two-dimensional unsteady fl ow of an incompressible viscous fl uid is governed by the wellknow Navier–Stokes equations where u≡u(x,y,t)and v≡v(x,y,t)are velocity components in the x-and y-directions,respectively.p≡p(x,y,t)is fl uid pressure and ν is kinematic viscosity.Here and further the subscripts denote partial differentiation with respect to corr

esponding variables.For simplicity,we can set ν=1 by choosing suitable units for length and time.

About a century ago,Prandtl found that boundary layers play an important role in determining precisely the flow of certain fl uids.[14]He demonstrated that for slightly viscous fl ows the viscosity plays a key role near boundaries,although it can be negligible in the most of the flow.For an incompressible two-dimensional viscous fl uid over a fl at plate with the latter taken as y=0,the unsteady laminar boundary-layer equations for fl ow of high Reynolds number are given by

In addition,for the stationary fl at plate,the boundary conditions can be taken as

The external inviscid fl ow w(x,t)is related to the pressure p through

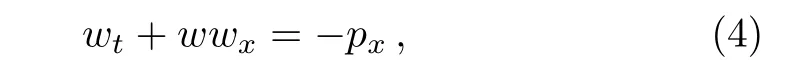
and it is usually obtained via inviscid fl ow calculations.Besides the boundary conditions,an initial value of u is needed to form a well-posed problem.However,in studying similarity solutions,the initial condition is determined rather than prescribed.

The quest for similarity reductions and exact solutions of the boundary-layer equations is signi ficant and also has a long history.[2,14−21]The motivation of the current paper is to perform symmetry analysis of the boundarylayer equations(2)along with the boundary conditions(3).A Lie subalgebra of the full symmetry group of the boundary-layer equations which also leaves the boundary conditions(3)invariant is considered.To get intrinsically different symmetry reductions and inequivalent group invariant solutions,a two-dimensional optimal system of the subalgebra is constructed.It is necessary to point that similarity reductions have many important values other than as mere mathematical exercises.Actually,reductions and exact solutions of physically important PDEs(including the boundary-layer equations)are signi ficant.Some exact solutions describe an important physical phenomenon and solutions of a system asymptotically tend to the solutions of the corresponding lower dimensional system obtained through similarity reductions.What is more,exact solutions also provide valuable checks on the accuracy and reliability of numerical algorithms.

The layout of this paper is as follows:In Sec.2,symmetry analysis and a two-dimensional optimal system of the boundary-layer equations(2)and(3)are presented.Then with aid of the optimal system obtained,symmetry reductions and exact solutions of the boundary-layer equations are performed in Sec.3.The last section is a short conclusion.

2 Construction of a Two-Dimensional Optimal System

2.1 Lie Algebra of the Boundary-Layer Equations

To perform Lie symmetry analysis of Eqs.(2),we consider the one-parameter Lie group of in fi nitesimal transformations in the form

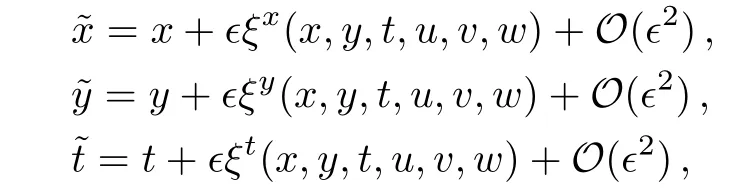
with ϵ≪ 1 is the group parameter.It is required that the set of solutions of Eqs.(2)is invariant under the transformation(5),which leads to a system of over-determined,linear equations for the in fi nitesimals ξx, ξy, ξt, ηu, ηv,and ηw.The associated Lie algebra of in fi nitesimal transformations is spanned by the set of vector fields

Here,the vector fields(6)have no relationship to the velocity variable v.For Eqs.(2),the solution of the determining equations is given by

where ci,i=1,2,3 are constants,r≡r(t)and s≡s(x,t)are arbitrary smooth functions,and the prime denotes derivative with respect to time t.So the Lie algebra of the symmetry group of Eqs.(2)is spanned by the following vector fields

Remark 1Comparing with Ovsiannikov’s solution,[2]one can see that his solution is not the most general solution as it loses the x dependence of the function s.Ma and Hui also get the Lie symmetry algebra of Eqs.(2).[20]Their solution is slightly different from our’s,as the calculation of the optimal system is simpler in terms of Eq.(8),so we consider(8)in this paper.

To leave the boundary conditions(3)invariant,[4]we must take r=constant and s=0.Hence,in the subsection,a subalgebra of Eq.(8)spanned by the following four vector fields will be considered

The commutation relations between the vector fields viand vjin Eq.(9)are given in Table 1.In which,the entry in row i and column j representing[vi,vj]=vivj−vjvi.

To compute the adjoint representation,we use the Lie series in conjunction with Table 1.Applying the formula

one can construct the following adjoint representation table with the(i,j)-th entry indicating Adexp(ϵvi)vj.

Table 1 Commutator table of the Lie algebra(9).

In conjunction with Table 2,the general adjoint transformation matrix A can be obtained,which is the product of the matrices of the separate adjoint actions A1,A2,A3,A4in any order and it is useful in the construction of an optimal system.The orders of the product of A1,A2,A3,A4are not important since only the existence of the elements of the group is needed in the algorithm.

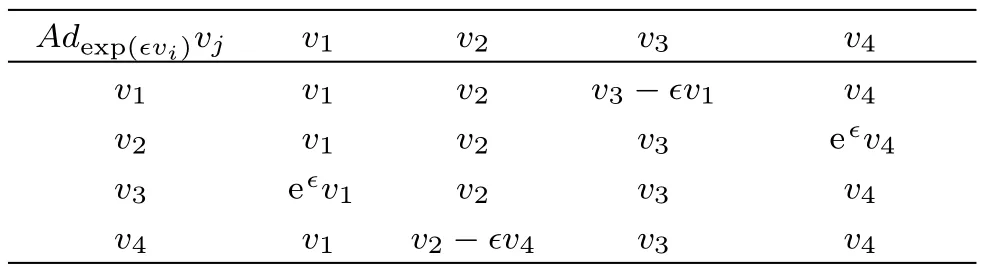
Table 2 Adjoint representation table of the Lie algebra(9).

Applying the adjoint action of v1to

we have

with

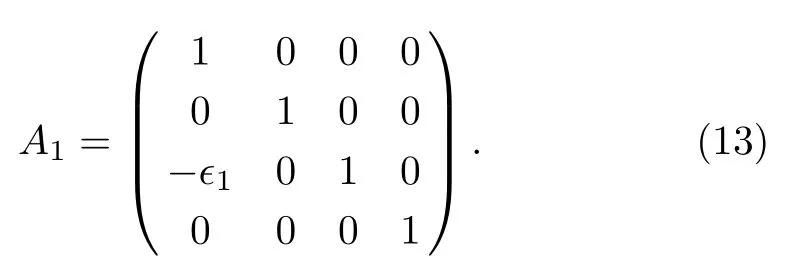
In a similar way,we can get A2,A3and A4,

So the general adjoint transformation matrix A is given by

2.2 Construction of a Two-Dimensional Optimal System

In this subsection,using the algorithm in Ref.[13],a two-dimensional optimal system of the Lie algebra(9)is constructed.First,we brie fl y recall the method.

Consider an n-dimensional Lie algebra G,which is spanned by the vector fields{v1,v2,...,vn}.The corresponding n-parameter Lie group of G is denoted as G.A family of two-dimensional subalgebras{gα}form an optimal system denoted as O2if:(i)A two-dimensional subalgebra is equivalent to some gα,and(ii)gαand gβare inequivalent for distinct α and β.Each element gα∈ O2is a collection of two linear combinations of the generators.Let

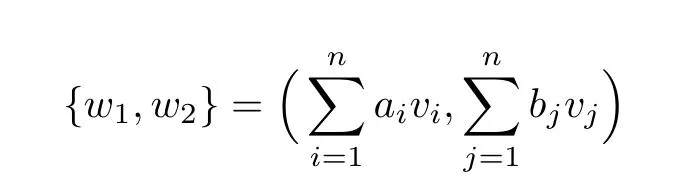
be a general two-dimensional subalgebra,which remains closed under commutation.Two elements{w1,w2}andare called equivalent if we can find some transformation g∈G and four constants k1,k2,k3,k4,such that

Sinceandare linearly independent,it requires that k1k4−k2k3/=0 in Eq.(16).In addition,for any element{w1,w2}∈O2,it requires that w1and w2constitute a two-dimensional subalgebra,i.e.[w1,w2]= λw1+ µw2with λ and µ being constants.Galas re fi nes this selection by demonstrating that w2must be an element from the normalizer of w1.That is to say we can select w2for[w1,w2]=λw1.Furthermore,for any two-dimensional subalgebra{w1,w2}with[w1,w2]=λw1,we can easily find an equivalent one=0 orHence,to find the inequivalent elements in the optimal system O2,without loss of generality,we require each member{w1,w2}∈O2satisfy[w1,w2]=0 or[w1,w2]=w1.It has been shown that for any two equivalent subalgebras{w1,w2}andthere is=0 if and only if[w1,w2]=0,=0 if and only if[w1,w2]≠0.For the later case,we have the following remark.

Remark 2 If two subalgebras{w1,w2}andwith[w1,w2]=w1andare equivalent in the form of Eq.(16),there must be k2=0 and k4=1.

To find all the inequivalent elements in the twodimensional optimal system O2,we first require each{w1,w2}∈O2satisfy

Thus,when take

the restriction(17)produces a set of equations of aiand bjfor two different cases.

For any two-dimensional subalgebra

a2n-dimensionalfunctionofϕ(a1,...,an,b1,...,bn)is called an invariant if it satis fi es ϕ(a11Adg(w1)+a12Adg(w2),a21Adg(w1)+a22Adg(w2))=ϕ(w1,w2)for all g∈G with a11,a12,a21,a22being arbitrary constants.

Taking a general subgroup g=exp(ϵv),(v=to act on w1,we have

in which(a1,...,an,c1,...,cn)can be easily get with the commutator table.In the same way,we have

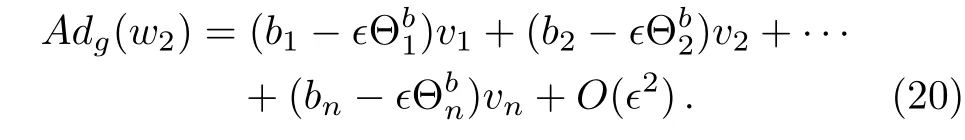
More intuitively,the following notations are adopted

For a two-dimensional subalgebra{w1,w2},according to the Definition of an invariant,we have

In addition,to guarantee a11Adg(w1)+a12Adg(w2)=w1and a21Adg(w1)+a22Adg(w2)=w2after the substitution of ϵ=0,it requires that

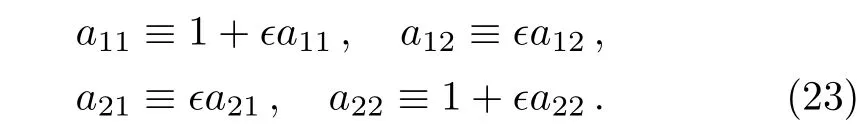
Thus Eq.(22)becomes

The following two distinct cases need to be considered to determine the invariants ϕ.

(i)When[w1,w2]=0,substituting(21)into Eq.(24),then taking the derivative of Eq.(24)with respect to ϵ and setting ϵ=0,extracting all the coefficients of ci,a11,a12,a21,a22,a set of linear differential equations about ϕ are achieved.Solving these equations,all the invariants ϕ on[w1,w2]=0 can be obtained.

(ii)When[w1,w2]=w1, firstly taking a12=0 and a22=0 in Eq.(24),then making the same procedure just as case(i).

For the Lie algebra(9),we take

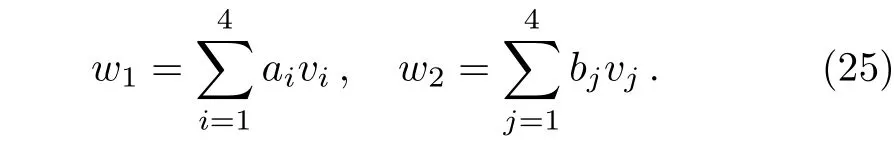
Let v=be a general element from G,in conjunction with Table 1,we have

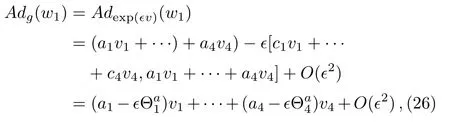
where

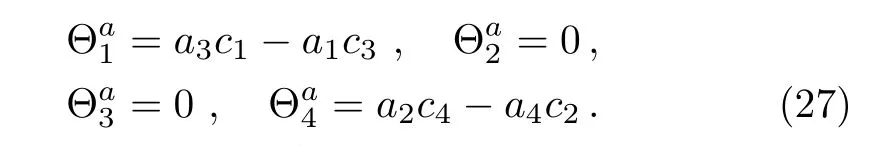
Similarly,applying v=to w2,we get

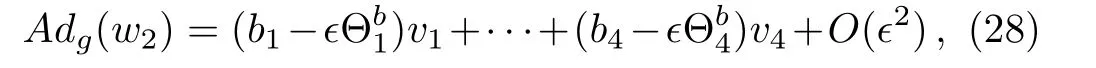
with

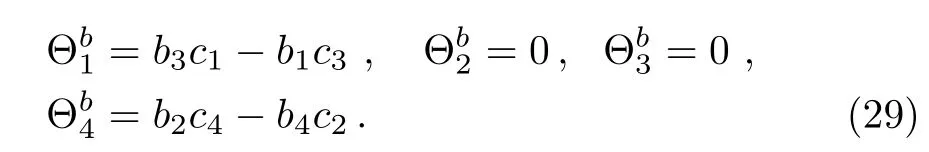
According to the algorithm,the following two cases need to be considered.

(i)When[w1,w2]=0,taking the derivative of Eq.(24)with respect to ϵ and then setting ϵ=0,extracting all the coefficients of ci(i=1,2,3,4),a11,a12,a21,a22,eight differential equations of ϕ ≡ ϕ(a1,...,a4,b1,...,b4)can be got,

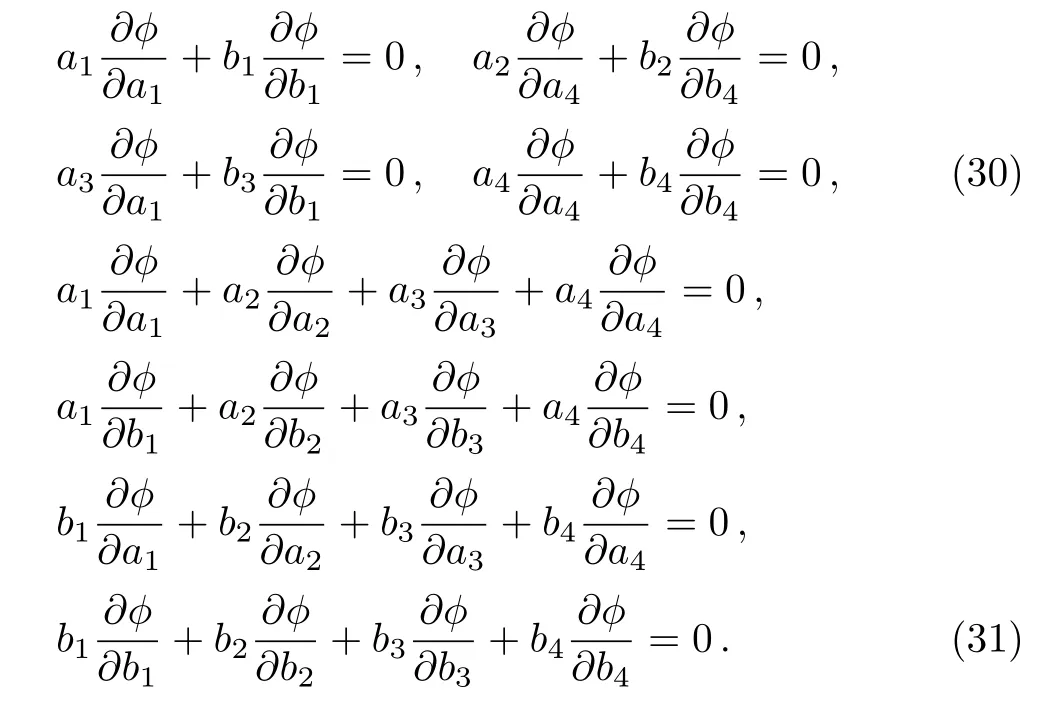
(ii)When[w1,w2]=w1,plugging a12=a22=0 into Eq.(24)and making the same process in case(i),six equations about ϕ are obtained,which are just Eqs.(30).

Substituting Eq.(25)into[w1,w2]=δw1,the following restrictive equations are obtained respective invariants and select the corresponding eligible representative elements For ease of calculations,we rewrite Eq.(16)as

For two distinct classes δ=0 and δ=1,in terms of every restricted condition given by Eqs.(32),compute their

More intuitively,Eqs.(33)are usually expressed as

where the general adjoint transformation matrix A is given in Eq.(15).If Eqs.(34)have solution with repect to(i=1,2,3,4),it implies that the selected representative elementis correct;if Eqs.(34)have no solution,another representative elementneed to be selected.Repeat the process until all the cases are if nished.

(i)The case of δ=0 in the restrictive equations(32).

Substituting δ=0 into Eqs.(32),we have

For this case,two different situations need to be considered.

Case 1 Not all a3and b3are zeros.Without loss of generality,we take a3≠0,then b1=a1(b3/a3).In this case,there exist three subclasses.

Case 1.1 When a2≠0,then we have b4=a4(b2/a2).Substituting b1=a1(b3/a3)and b4=a4(b2/a2)into Eqs.(30)and Eqs.(31),we find that ϕ=constant.The representative element{v2,v3}can be selected,since Eqs.(34)have the solution

Case 1.2 When a2=0,b2≠0,then it must have a4=0.In a similar way,we find that ϕ=constant.We select the representative element{v3,v2},then Eqs.(34)have the solution

It is obvious that Cases 1.1 and 1.2 are equivalent.

Case 1.3 When a2=b2=0.In this case,{v4,v3}can be selected as the representative element since Eqs.(34)hold for

Case 2When a3=b3=0.This case can be further divided into two subclasses.

Case 2.1Not all a2and b2are zeros.Without loss of generality,we take a2≠0,then b4=a4(b2/a2).We choose a representative element{v1,v2},then Eqs.(34)have the solution

Case 2.2 When a2=b2=0,{v1,v4}can be selected as the representative element since Eqs.(34)hold for

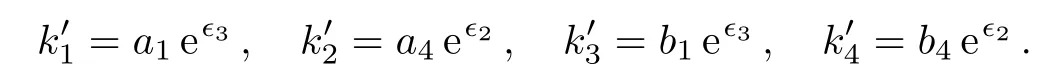
(ii)The case of δ=1 in the restrictive equations(32).

Substituting δ=1 into Eqs.(32),it must have a2=a3=0.Then Eqs.(32)become to

Case 3When a1=0,it must have a4≠0,thus we get b2=1.In this case,by solving Eqs.(30),we get an invariant ϕ = ∆1=b3.This case can be further divided into two subclasses according to the values of∆1.

Case 3.1 If∆1= α/=0,we can select the representative element{v4,v2+αv3},then Eqs.(34)have the solution

Case 3.2 If∆1=α=0,there exist three circumstances in terms of the sign of b1.

(a)When b1＞0,{v4,v1+v2}can be chosen as the representative element since Eqs.(34)hold for

(b)When b1<0,we select the representative element{v4,−v1+v2}and Eqs.(34)have the solution

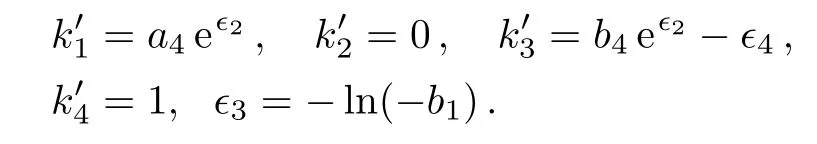
(c)When b1=0,we select the representative element{v4,v2}and Eqs.(34)hold for

Case 4When a1≠0,a4=0,then we have b3=1.In this case,by solving Eqs.(30),we get an invariant ϕ=∆2=b2.This case can also be further divided into two subclasses according to the values of∆2.

Case 4.1If ∆2= α/=0,we select the representative element{v1,αv2+v3},then Eqs.(34)have the solution

Case 4.2 If∆2=α=0,there exist three circumstances in terms of the sign of b4.

(a)When b4＞0,{v1,v3+v4}can be chosen as the representative element since Eqs.(34)hold for

(b)When b4<0,we select the representative element{v1,v3−v4}and Eqs.(34)have the solution

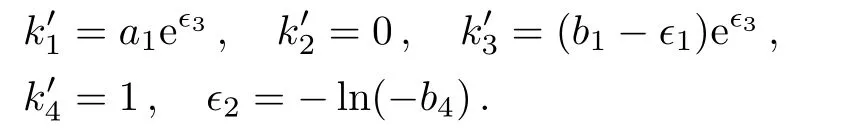
(c)When b4=0,we select the representative element{v1,v3}and Eqs.(34)have the solution

Case 5 When a1≠0,a4≠0,then we have b2=b3=1.Solving Eqs.(30),we find that ϕ=constant.In this case,there exist two circumstances in terms of the sign of a1a4.

(a)When a1a4＞0,we select the representative element{v1+v4,v2+v3}and Eqs.(34)have the solution

(b)When a1a4<0,{v1−v4,v2+v3}can be chosen as the representative element since Eqs.(34)hold for

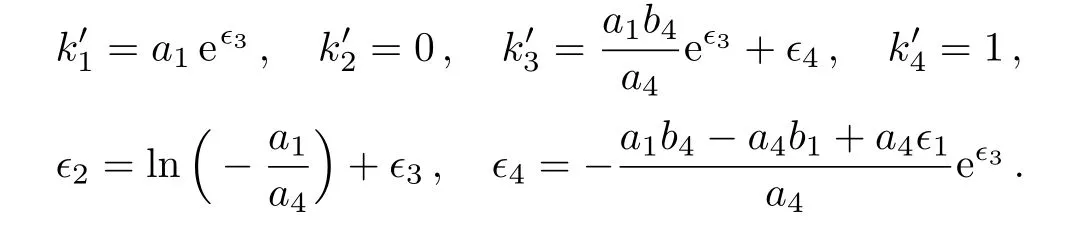
In summary,a two-dimensional optimal system O2of the Lie algebra(9)is obtained

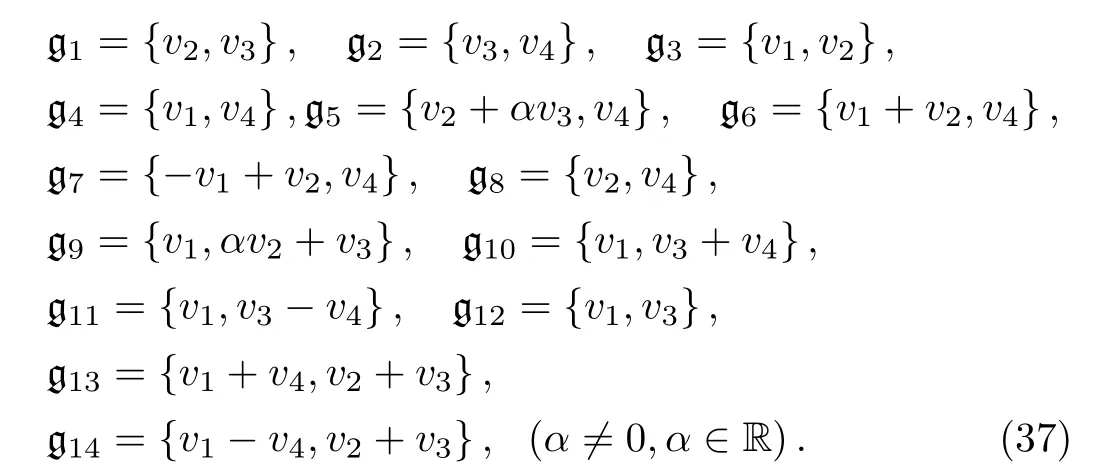
The value in parentheses does not denote disallowed value,it denotes the value of the parameter that needs not to be considered,because it is considered elsewhere.This information is important in the calculation of the similarity variables.

3 Symmetry Reductions and Exact Solutions

By virtue of the two-dimensional optimal system O2(37),the boundary-layer equations(2)and(3)can be directly reduced to different classes of ODEs.This is achieved by solving the invariant surface condition equations to find all the similarity invariants,which are then used as new variables.

For g1={v2,v3},the invariant surface condition equations are given by

Solving Eq.(38),we have

where z=is a similarity variable.Substituting Eq.(39)into Eqs.(2),a system of ODEs is obtained

The boundary conditions(3)then require

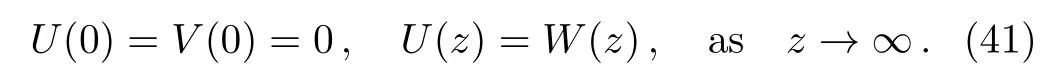
From the third equation in Eq.(40),we conclude that W(z)=E,Eis a constant.Using the transformation V(z)= −Ef(z),from Eqs.(39)–(41),we can get

where f(z)satis fi es

This solution has been obtained by Ma and Hui,they refer this solution as the unsteady separated staparated-point flow solution(USSP)and study it in detail.

In a similar way,for g2={v3,v4},an analytic solution can be obtained

where C is an arbitrary constant.It is easy to verify that this solution also satis fi es the Navier–Stokes equations(1)with the pressure given by

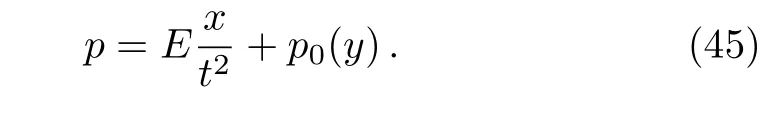
For g3={v1,v2},it is easy to get

where f(y)satis fi es

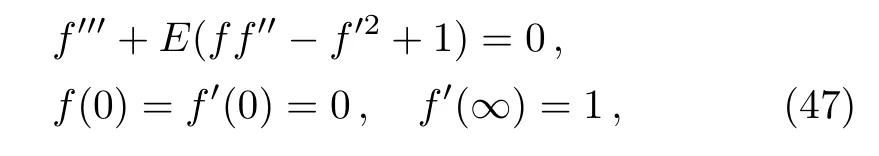
which is the Hiemenz stagnation-point fl ow solution.

By virtue of g5={v2+ αv3,v4}(α/=0),we can get that

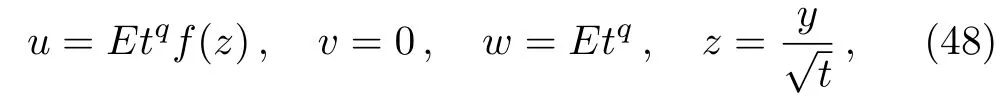
with f(z)satis fi es

where q=1/α−1.The solution given by Eqs.(48)and(49)also satis fi es the Navier–Stokes equations(1)with the pressure

An analytic solution of Eq.(49)is given in Ref.[20]when q is a positive integer.Here,we consider three special cases when q is not a positive integer.

When α=1(q=0),Eq.(49)admits an error function solution

where the error function erf(x)is de fi ned as

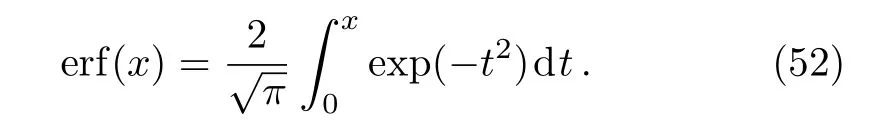
This case results in the Rayleigh solution.

When α=2/3(q=1/2),Eq.(49)has a solution of the form

In this case,the stream function Ψ of the fl ow Eq.(48)is given by

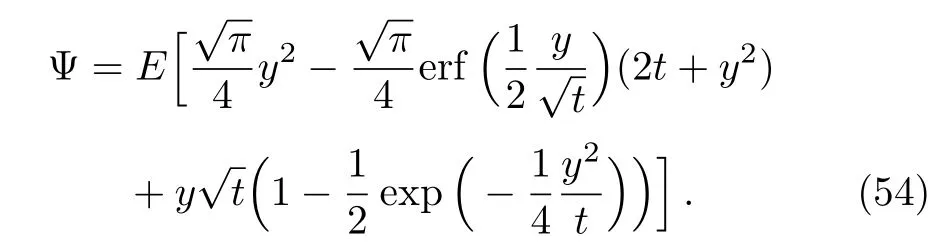
When α =2(q= −1/2),another solution of Eq.(49)is obtained

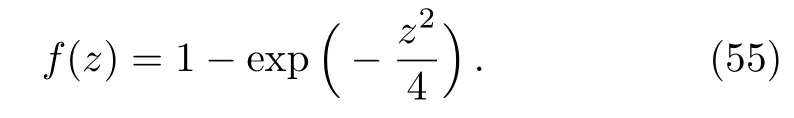
For this case,the stream function Ψ is given by

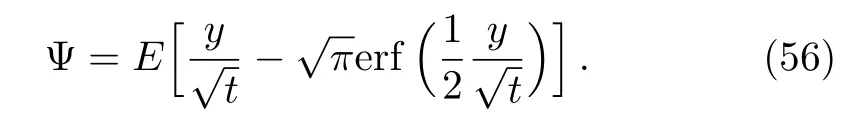
The solutions(53)and(55)are not reported in Ref.[20].More analytic solutions to Eq.(49)for other values of α can also be obtained,but for brevity,we do not present here.

From g6={v1+v2,v4},the following solution can be achieved

The solution(57)also satis fi es the Navier–Stokes equations(1)with the pressure

For g13={v1+v4,v2+v3},we get

where f(z)and g(z)satisfy

In addition,by the transformation f(z)=(1/E)(1−h′(z)),Eq.(60)can be converted to

With g(z)is given by

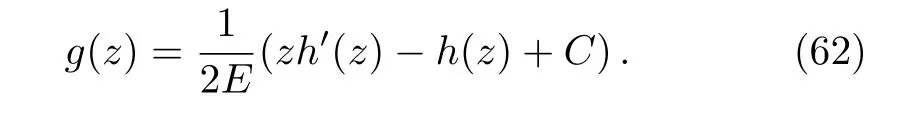
From Eq.(62),it is obvious that g(0)=0.

For g14={v1−v4,v2+v3},we have

where f(z)and g(z)satisfy

Similarly,by the transformation f(z)=(1/E)(h′(z)− 1),Eqs.(64)become to

In this case,g(z)also meets(62).These two reductions from g13and g14are not obtained in Ref.[20],as far as we know,they may be previously unknown.

More reductions and exact solutions of the boundarylayer equations can be found by virtue of the other elements in the optimal system(37).For instants,using g9,g10,g11and g12,the steady boundary-layer fl ow solutions may be obtained.For volumes,we do not present here as all the existing group invariant steady solutions have been listed in Ref.[20],and no new group invariant solutions can be found.While only trivial solution can be found from g4,g7and g8.

4 Conclusion

In conclusion,the boundary-layer equations which are important models in fl uid mechanics are studied through the classical Lie symmetry method.Its symmetry group is narrowed down to a subgroup under which the boundary conditions are also invariant.To find intrinsically different similarity reductions and inequivalent group invariant solutions,a two-dimensional optimal system is constructed.Since all the representative elements in the optimal system are attached to different values of the invariants,it can ensure the optimality of the optimal system obtained,need no further proofs.We notice that in almost all of the existing literatures,a one-dimensional optimal system is required for the construction of a two-dimensional optimal system,which usually takes too much work.In this paper,the construction starts from the Lie algebra directly and only depends on fragments of the theory of Lie algebras,without a prior one-dimensional optimal system.Then with the aid of the optimal system,some symmetry reductions and exact solutions of the boundary-layer equations are obtained.It has been shown that not only do we recover many of the known results but also find some new solutions,which may be previously unknown.In Ref.[20],the authors investigated the boundary-layer equations using a two-step reduction procedure,and some of the reductions obtained are overlapped.In our paper,due to the two-dimensional optimal system,the original equations are reduced to a system of ODEs via only one step.What is more,the reduced systems are intrinsically different and the solutions obtained are inequivalent,and some repetitive works are also avoided.

As we know,the nonclassical symmetry(also known as conditional symmetry)method generalizes and includes the classical method in studying reductions and solutions of PDEs.[5]So the nonclassical symmetry analysis of the boundary-layer equations may generate more new solutions,which is interesting and deserves our further study.

References

[1]S.Lie,Arch.Math.6(1881)328.

[2]L.V.Ovsiannikov,Group Analysis of differential Equations,Academic,New York(1982).

[3]P.J.Olver,Applications of Lie Groups to differential Equations,Springer,New York(1993).

[4]G.W.Bluman and S.C.Anco,Symmetry and Integration Methods for differential Equations,Springer,New York(2002).

[5]G.W.Bluman and J.D.Cole,J.Math.Mech.18(1969)1025.

[6]X.R.Hu,Z.Z.Dong,F.Huang,and Y.Chen,Z.Naturforsch.A 65(2010)504.

[7]Z.Z.Dong,F.Huang,and Y.Chen,Z.Naturforsch.A 66(2011)75.

[8]Z.Z.Dong,Y.Chen,D.X.Kong,etal.,Chin.Ann.Math.B 33(2012)309.

[9]K.S.Chou,G.X.Li,and C.Z.Qu,J.Math.Anal.Appl.261(2001)741.

[10]K.S.Chou and C.Z.Qu,Acta Appl.Math.83(2004)257.

[11]Q.Huang and C.Z.Qu,J.Phys.A:Math.Theor.40(2007)9343.