Electron-Positron Pair Production in Strong Fields Characterized by Conversion Energy∗

Ibrahim Sitiwaldi,Zi-Liang Li(李子良),and Bai-Song Xie(谢柏松),2,†College of Nuclear Science and Technology,Beijing Normal University,Beijing 00875,China

2Beijing Radiation Center,Beijing 100875,China

1 Introduction

In quantum electrodynamics(QED),it was predicted that an external energy associated with a strong field can be converted into matter in the form of electron-positron pairs.Schwinger calculated the rate of pair production in the constant electric field using a non-perturbative approach[1]after the earlier works of Sauter,[2]Heisenberg and Euler.[3]Although the threshold of field strength is too high to reach up now,it is possible to detect the fascinating phenomena of light to directly convert into matter in the near future with the rapid development of laser technology,for example,the European extreme-lightinfrastructure(ELI)program is now advancing.[4]Therefore,the active theoretical study on electron-positron pair production is important to support the upcoming experiment.

The Dirac equation for a force-free electron has positive solutions of energy continuumEp≥mec2as well as negative solutions of energy continuumEn≤−mec2.We call them positive states and negative states,respectively.All the positive states are empty and all the negative states are occupied in the Dirac see.In the presence of an external field there are mainly two different production mechanisms under which an electron in the negative state can get enough energy from the external field to jump into a positive state and leave behind a “hole” which is also called a positron.The first mechanism is the tunneling e ff ect,[1]it requires the external field to reach the Schwinger limit ofEc=1.32×1018V/m,The second mechanism is photon absorbtion[5−7]where time-dependence of the external field can induce quantum transitions with a key role of the photon energy.

In past decades many theoretical methods have been employed to study electron-positron pair production,such as proper time method,[8−10]WKB approximation[11]and worldline instanton techniques.[12−13]Quantum field theoretical simulations[14−15]in the spatial and temporal inhomogeneous external field[16−24]as well as the quantum kinetic method[25−26]in the spatial homogenous and timedepending external field[27−30]received a great deal of interest in recent years.

Study on the pair production in oscillating electric fields[31]indicates an interesting dependence of pair creation rate to the characteristic parameters associated to the tunneling or/and multiphoton processes.On the other hand in a bifrequent fields[32−34]as well as in a combined fields[35−37]the studies have shown more complicated production process composed of various production channels.So it should be important to know first that what mechanism induce or dominate the pair yielding.

In order to represent the physical picture of a pair production process,which is still a challenging task in a more realistic and complicated field con fi guration,in this paper,we try to suggest a simple and uni fi ed method to reveal clearly the pair production process by focusing on what mechanism dominates and how the production channels are identi fi ed.We introduce first the conversion energy for a pair produced in the external field.And then we demonstrate that it is directly associated with the production mechanism of this pair.To test the feasibility of conversion energy we study the spectrum of conversion energy for the electron-positron pair production process in a static and an oscillating field via quantum field theoretical simulations in the one-dimensional space.Finally we study the pair production in a bifrequent and a combined field in the view of conversion energy.

The paper is organized as follows:In Sec.2 we introduce the conversion energy term and its spectrum after a brief review of the computational framework.In Sec.3 we analyze the numerical results.In the last section we provide a brief conclusion.

2 Theoretical Method

2.1 The Quantum Field Theoretical Simulations

To study the electron-positron pair production process,the relativistic quantum mechanical Dirac equation for a single-particle wave function is not sufficient as it assumes the existence of a particle from the beginning and the unitary time evolution would make it impossible to describe for which the number of particles can change.We employ the quantum field theoretical simulations to describe particle creation and annihilation processes in external field.We neglect the fermion interaction and work in a one-dimensional space for computational reason.We use the natural units(~=c=1)in this paper where the electron quantities as the normalized units,i.e.,length λc=1/me=3.862 × 10−13m,time 1/me=1.288×10−21s,frequency me=7.764×1020Hz,momentum me=2.73 × 10−22kg·m/s,energy me=0.511 MeV.

The electron and positron are described by Dirac field operator that satis fi es the time-dependent Dirac equation,where V(z,t)denotes the electric potential associated with the external field acting and varying along z direction.There is no spin change in one dimension so fourcomponent Dirac spinor reduce to only two components and Dirac matrices is replaced by the usual Pauli matrices σ.We rede fi ne pz=p for simplicity.

The time-evolved Dirac operator may be expanded in terms of the electron annihilation and positron creation operators and the force-free positive and negative energy eigenstates,

where Wp(z)and Wn(z)represent the field-free energy eigenstates|pand|nin the spatial representation at t=0,Wp(z,t)and Wn(z,t)satisfy the single-particle time-dependent Dirac equation Eq.(1).From Eq.(2)we obtain

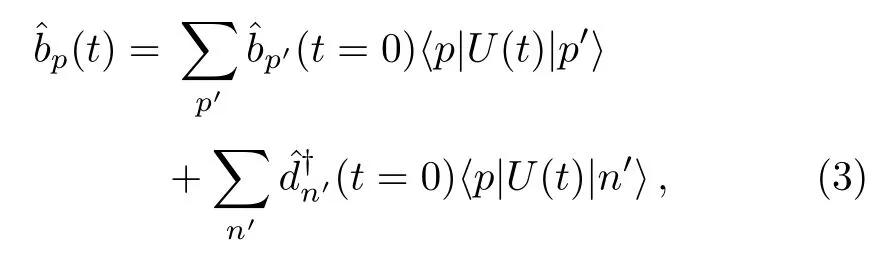
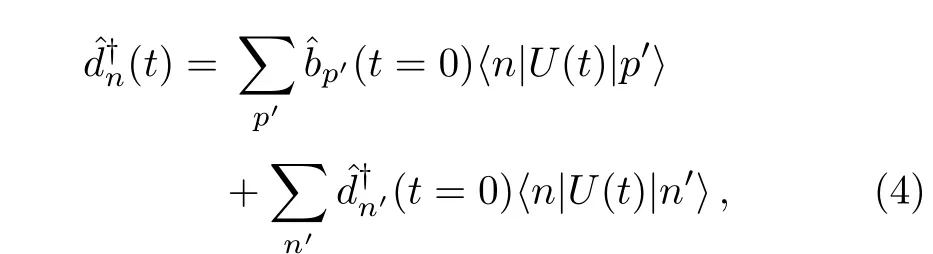
where the coefficients are the elements of the time-ordered propagator U(t)=exp[−i∫tdt′[cσ1p+ σ3me+V(z,t′)]]between the energy eigenstates.The field operator also can be expanded by the instantaneous eigenstates of timedependent Hamiltonian.The interpretation of physical quantities derived from Dirac field operator depends on its expanding basis.[38]For our case where Dirac operator is expanded in terms of free particle states,we would have to regard all the quantities derived below as those properties that produced particles would take if the external field was instantaneously turned o ff.

The produced electrons’spatial density can be obtained from the expectation value of the product of the electronic field operators,

whereis the electronic portion of the field operator.Using the commutator relationsthe density can be expressed through the field-free energy eigenstates of the single-particle Hamiltonian as

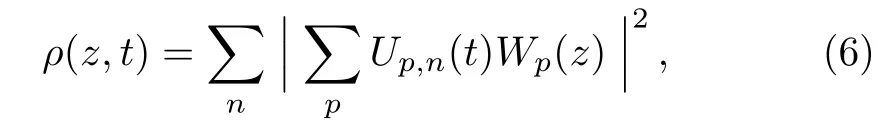
where Up,n= 〈p|n(t)= 〈p|U(t)|ncan be computed by using the split operator numerical technique.[14]By integrating Eq.(6)over space,we obtain the total number of the produced pairs as

2.2 Conversion Energy and Its Spectrum

The mass-energy of a pair produced from the vacuum in an external field can be expected to be equal to the energy it has absorbed from the external field.Note that it should be a physical process,which includes the possible inverse process of the matter to convert into energy as long as the energy conservation holds.For a pair produced in a pair production process,we take the sum of mass-energy of the electron and its conjugate positron and de fi ne it as conversion energy,

where p and n are momentum of the electron and its conjugate positron,respectively.Equivalently,one can regard the conversion energy as follows:the electron in a negative state with energyEn=jump into a positive state with energyEp=absorbing energyEp,n=Ep−Enfrom external field.

The expectation number of a pair of electron with momentum p and positron with momentum n produced at time t is|Up,n(t)|2,which is given above.According to our interpretation in the last subsection,one has to regard the conversion energy Eq.(8)as the total mass-energy the produced pair would take if the external field was turned o ffabruptly.We calculate the conversion energyEp,nand corresponding yields|Up,n(t)|2of produced pairs for all p and n and represent them in term of distribution of pair numbers as a function of the conversion energy,p(E,t),

3 Numerical Results

We simulate the pair production processes for different field con figurations and discuss the production mechanism in the view of conversion energy.

A symmetric potential well is illustrated asV(z,t)=V(t)S(z)for external field in our simulations,whereV(t)is potential height and S(z)={tanh[(z− D/2)/W]−tanh[(z+D/2)/W]}/2 is the Sauter-type potential well,W is a measure for the width of each edge,D is the total extension of the potential well.

For all simulations in this paper,we take W=0.3,D=8,the length of simulation space L=340 withNz=4096 grid points,total simulation time t0=40π withNt=4000 grid points.For the calculation of CES,Eq.(9),we takeNE=1000 grid points in abscissaEand take∆E=0.04 to get more sensitive and smooth curves.

3.1 The Pair Production in a Static Electric Field

We discuss the pair production process dominated by the Schwinger mechanism to study how to characterize this process in the view of conversion energy.

In Fig.1 we display final(after external field is turned o ff)CES of the pairs produced in a static field with potential heightV=2.5,where the tunneling e ff ect[1]is responsible for the production process.There are a peak corresponding to potential height and it contains the most yields.The peak position is 2.46,with the agreement of 1.6%with the potential height,average conversion energy of total yields is 2.58,with the agreement of 3.2%with the potential height.We repeat this simulation for the static fields with potential heightsV=3,3.5 and obtain graphics very similar to Fig.1 except the peak positions at 2.94,3.44,respectively.

The distribution is a bit higher unexpectedly in the left side of the peak,within the area from 2.18 to 2.38,it shows that there are some pairs still inside the interaction zone and have lower conversion energy,one has to be careful that there are still some interpretational challenge about particles inside interaction zone.There is also small amount of distribution out of the peak,we believe there are some pairs produced in the beginning due to dramatic turning on the external field as we discuss below.

In the inset of Fig.1 we display CES of the pairs produced shortly after(when t=0.01t0)turning on the external field.It is very different from the main fi gure,most of these pairs have too large or too small conversion energy to be produced by the tunneling process,indicating there is other production mechanism.We attribute it to high frequency Fourier components of the external field turning on dramatically.This phenomena is studied in a more systematic way in the next subsection.

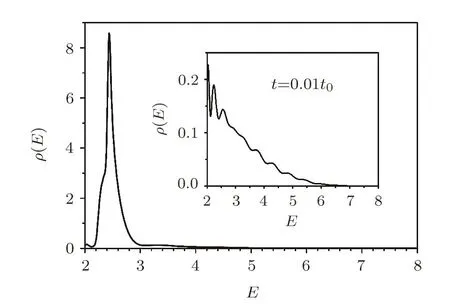
Fig.1 Final CES of the pairs produced in a static field with potential height V=2.5,the inset is CES shortly after turning on the electric field.

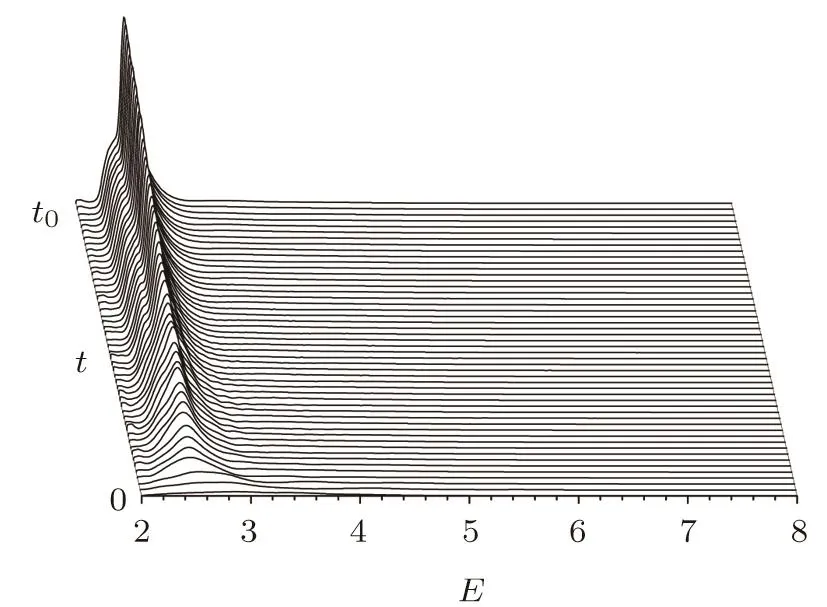
Fig.2 Waterfall of CES of pairs produced in a static field with potential height V=2.5 in times t=(n/50)t0 with(n=1,2,3,...,50).

To represent time evaluation of the conversion energy,in Fig.2 we display the waterfall of CES of pairs produced in a static field with potential heightV=2.5 in times t=(n/50)t0(n=1,2,3,...,50).The peak is generated at the expected position in the very beginning and keeps the position unchanged.It can be shown that the production mechanism is consistent all the interaction time.

The conversion energy of the pair produced in a static field agree with the physical picture of the tunneling effect,the electron in the negative energy continuum travels through the edge of potential well to join to the positive energy continuum,absorbing energy in the amount of potential height from external field.The conversion energy of a pair produced by tunneling process in the static field with potential height V can be expressed as

3.2 The Pair Production in an Oscillating Electric Field

Now we study pair production process in the timedepending subcritical electric field,where the photon absorbtion[5−7]can be responsible for the pair production.We separately study production channels corresponding to each order of transition in the view of conversion energy.

In Fig.3(solid line)we display final CES of the pairs produced in a oscillating field with amplitude V=1.5 and frequency ω=1.3,where the potential height oscillates as V(t)=V sin(ωt).Most yields are distributed within four narrow peaks,the positions of them areE2=2.61,E3=3.90,E4=5.21,andE5=6.50,respectively.These peaks represent the two,three,four,and fi ve-photon processes.The corresponding yields are 60.9%,29.6%,8.19%,and 1.32%of total yields 1.73,respectively,where the yields of each process is obtained by integrating corresponding peaks.The yields due to lower order photon absorbtion is more than of higher order photon absorbtion because the chance of absorbing large number of photons is smaller than the chance of absorbing small number of photons in the view of perturbation theory.[21]

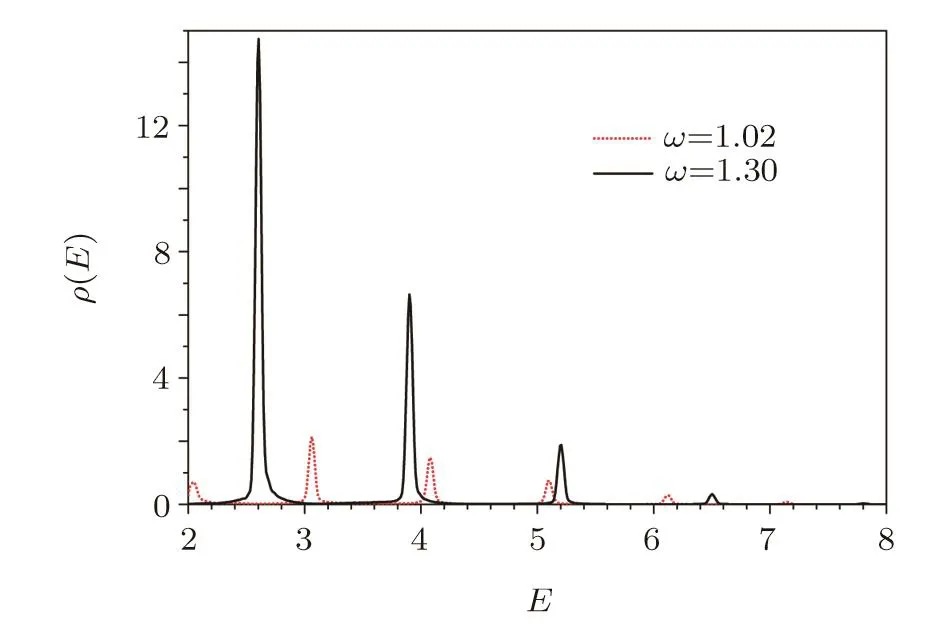
Fig.3 (Color online)Final CES of the pairs produced in oscillating field with amplitude V=1.5 for two different frequencies.

Figure 3 is similar to multiphoton peaks in Ref.[39],but there are a signi ficant di ff erence,instead of momentum of positron we take the exact mass-energy of electron and its conjugate positron to represent how much energy this pair absorbed from external field.It is need to remind that a pair may interact again with the electric field once it is created and absorb more photons to contribute a high-order process so the physical picture of the highorder process is still not very clear.For example,we are unable to decide that a pair corresponding to the peak atE=3.90 in Fig.3 absorb three photons during its creation or absorb one more photon after created by a two-photon process.

The signature of e ff ective mass in multiphoton pair production was discussed in Ref.[40]and demonstrated that the frequency threshold of n-photon process is higher than 2me/n due to e ff ective mass.We repeat above simulation with frequency ω=1.02 and display corresponding CES in Fig.3(dashed line),all features agree with our discussion about ω=1.3 except the rather small peak atE=2.04 corresponding to the two-photon process.We believe that frequency threshold increased due to e ff ective mass can be responsible for this suppression.

In order to describe the multiphoton process during all the simulation time we display the waterfall of CES of the pairs produced in an oscillating field with amplitude V=1.5 and frequency ω=1.3 in times t=(n/50)t0(n=1,2,3,...,50)in Fig.4.All the peaks are generated from very beginning and the peak positions keep unchanged while the peak heights linearly increase following the simulation time,representing the production process with constant production mechanism almost all the interaction time.

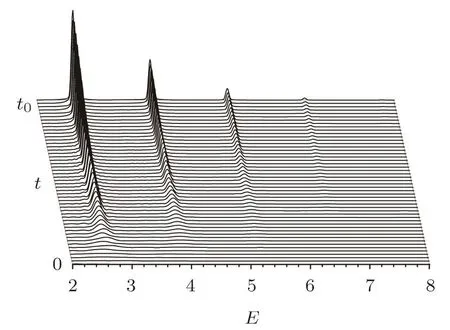
Fig.4 Waterfall of CES of the pairs produced in an oscillating field with amplitude V=1.5 and frequency ω=1.3 in times t=(n/50)t0with(n=1,2,3,...,50).

The production process associated with each order of photon absorbtion in a time-depending external field with frequency ω can be identi fi ed speci fically by the conversion energy,which reads as follows for a pair produced by n-photon process,

Studying a certain production channel individually is convenient with it.We study a temporal behaviour of each production channel now.

Integrating corresponding peaks in every time steps we obtain the yields of each production channels as a function of time.In Fig.5 we represent time-dependence of the yields of each production channel in oscillating field with frequency ω=2.1 and amplitude V=1.5.We can see that there are some di ff erence in temporal behaviour of each production channel.The production rate of onephoton process decrease in early time(before t=30),while other high-order processes keep almost constant production rate,causing to decrease total production rate,where production rate(dN(t)/dt)is represented by the gradient of corresponding curves in Fig.5.

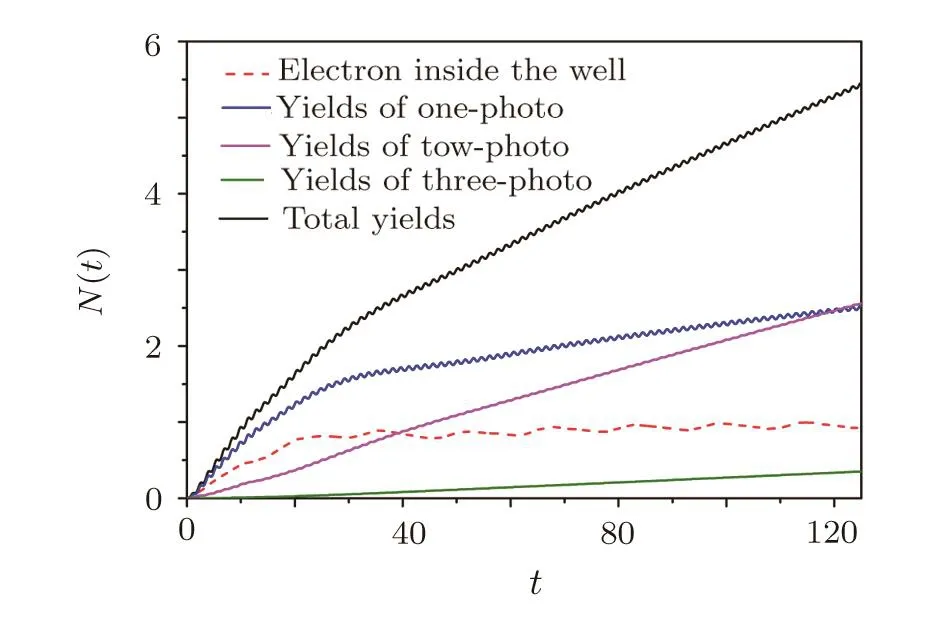
Fig.5 (Color online)The yields of each production channel as a function of time in oscillating field with frequency ω=2.1 and amplitude V=1.5.

We suppose that the suppression of production rate can be attribute to Pauli block and investigate the relation between suppression of production rate and pair number inside the well to test it.The yields of electrons inside the potential well as a function of time is represented by the dashed line in Fig.5,which is obtained integrating Eq.(6)inside the well.It can be seen that the number of electrons inside the well increases from 0 to about 0.75 up to t=30 and then almost keeps unchanged,while the production rate of total yields and one-photon process is decreasing before t=30 and then almost keep unchanged.It is safe to say that the production rate of one-photon process is suppressed by particles inside the well.We believe that the production of high-order processes have two sources,one is production from vacuum by multiphoton process,which can be suppressed by pairs inside the well like one-photon process,another one is acceleration of yields inside the well,which is proportional to the number of pairs inside,so there is no decrease of production rate of high-order processes.

We mention in the last subsection that adiabatic turning on electric field can trigger pair production.Accordingly,one can expect that turning on and o ffexternal field periodically may also trigger a continuously pair production.We simulated the pair production in a binary pulsed field where a static field with potential height V=1.5 turned on and o ffperiodically with frequency ω=1.3.The time evolution of this field can be expressed as V(t)=V θ(sin ωt)where θ denotes heavyside step function.The time evolution of the yields in Fig.6(inset)indicates a continues production.We discuss the production mechanism of this process with the help of final CES in Fig.6(main).There are multiphoton peaks corresponding to sinusoidal components of the binary field,which may be expanded in terms of Fourier components as

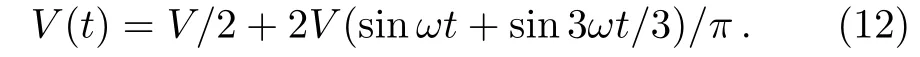
The multiphoton peaks corresponding to first sinusoidal term in Eq.(12)is atE=2.59,3.90,5.20 where the peak atE=3.90 is superimposed by a peak corresponding to second sinusoidal term in Eq.(12)in the same time.It can be demonstrate that a non-sinusoidal time-dependent electric field can also trigger a pair production processes associated with photon absorbtion due to its sinusoidal Fourier component.This result con fi rms our assertion about turning on electric field dramatically in last subsection.

Fig.6 Final CES of pairs produced in a binary pulsed field where a static field with potential height V=1.5 turned on and o ffperiodically with frequency ω=1.3,the inset is time evolution of the yields.

3.3 Pair Production in a Bifrequent Electric Field

Electron-positron pair production in a bifrequent electric field composed of a strong low-frequency and a perturbative high-frequency mode was studied in Ref.[32],a resonant behavior depending on the frequency composition of the field was found,which indicates pair production triggered by the combination of different photons.We investigate the composition of production channels in a bifrequent field.

In Fig.7(Solid line)we display final CES of the pairs produced in a bifrequent field composed of two oscillating fields with amplitudes V1=V2=1.5 and frequencies ω1=1.3,ω2=1.5,where the total potential height is V(t)=V1sin(ω1t)+V2sin(ω2t).There are many narrow peaks with different heights,indicating the existence of rather complicated production channels.The two,three,four-photon processes triggered by photon with frequency ω1denoted as ω1,2ω1,3ω1are represented by the peaks atE=2.61,3.90,5.20 respectively,matching with corresponding number of photon energy perfectly.The two,three,four-photon processes triggered by photon with frequency ω2denoted as ω2,2ω2,3ω2are represented by peaks atE=3.00,4.50,6.01 respectively.

As we expect we detect the process of photon absorbtion triggered by the combination of different photons here.The corresponding two-photon process denoted as ω1+ ω2,three-photon processes denoted as 2ω1+ ω2,ω1+2ω2,and four-photon processes denoted as 3ω1+ω2,2ω1+2ω2, ω1+3ω2are represented by the peaks atE=2.80,4.10,4.30,5.40,5.60,5.81,respectively.We neglect to discuss the peaks with rather small heights,which are corresponding to higher order processes.

Fig.7 (Color online)Final CES of the pairs produced in a bifrequent field composed of two oscillating fields with amplitudes V1=V2=1.5 and frequencies ω1=1.3,ω2=1.5.

We find some peaks with unexpected positions in Fig.7.For example,the production mechanism of pairs corresponding to the peak atE=2.42 can not be regard as a pure photon absorbtion since its corresponding conversion energy can not be expressed as a sum of any positive integer number of ω1and ω2,but matches 3ω1− ω2very well.We explain the production process as absorbing three photons with frequency ω1and emitting one photon with frequency ω2,but we are still unable to decide that during production or after production it emits a photon.These peaks atE=3.19,3.71,4.69 can also be explained in the similar way with the processes denoted as 3ω2−ω1,4ω1−ω2,and 4ω2−ω1respectively.The underlying physical mechanism of these findings need to study further in future.

It can be demonstrated that in a bifrequent field with frequencies ω1,ω2the multiphoton process can be triggered by the combination of same photons as well as different photons,the corresponding production channel can be identi fi ed by the conversion energy of the produced pair,where n1,n2are integer satisfyingE(ω1,ω2)≥ 2.

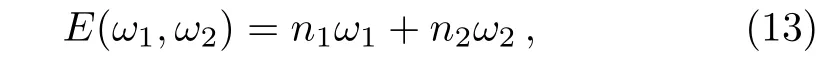
For comparison we also display the CES for each single frequent field individual in Fig.7(dashed lines).The yields of production process associated only to one frequency in the bifrequent field is less than the yields of the same process in the single frequent field individual,we attribute it to the competition between the various production channels in the bifrequent field.

3.4 Pair Production in a Combined Electric Field

It was demonstrated that the pair production rate can be enhanced in a combined field composed of a strong slow-varying and a perturbative high-frequent field due to dynamically assisted Schwinger mechanism.[30]We simulate the pair production in a combined field to detect the signature of dynamically assisted Schwinger mechanism and investigate the exact contribution of each production channel with the help of conversion energy.

In Fig.8 we display final CES of the pairs produced in a combined field composed of a static field with potential height V=1 and an oscillating field with amplitude V1=1,frequency ω=1.3,dashed lines are for each individual field,where the final yields of combined field,static field alone and oscillating field alone are 1.33,0.41,and 0.02,respectively.

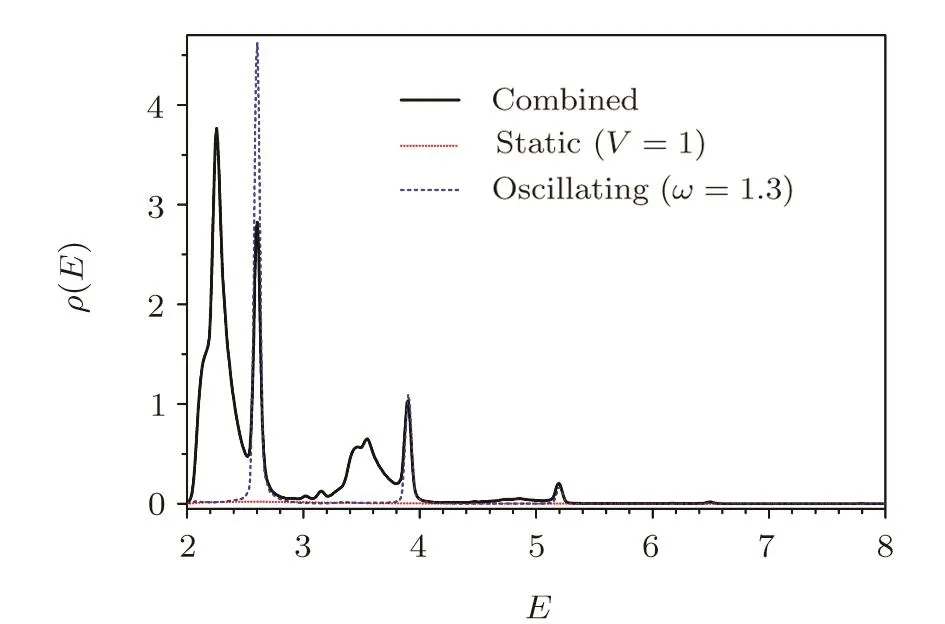
Fig.8 (Color online)Final CES of the pairs produced in a combined field composed of a static field with potential height V=1 and an oscillating field with amplitude V1=1,frequency ω=1.3.

There are four narrow peaks atE=2.61,3.90,5.20,6.50 representing two,three,four,and fi ve-photon processes denoted as 2ω,3ω,4ω,5ω.As we expect,we detect the processes of dynamically assisted Schwinger mechanism denoted as ω +V,2ω +V,3ω +V,which are represented by the peaks atE=2.25,3.55,4.86 respectively.The production channel corresponding to a pair can be identi fi ed according to the conversion energy of this pair,

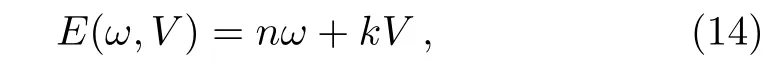
where k=1 for dynamical assisted Schwinger mechanism and k=0 for pure photon absorbtion,n is integer satisfyingE(ω,V)≥ 2.

Integrating corresponding peak we can obtain the yields of each production channel in combined field.The yields corresponding to dynamically assisted Schwinger mechanism is 0.94,71%of total yields 1.33,which is essential to the enhancement of production rate.The peak corresponding to pure photon absorbtion in combined field is smaller than the corresponding peak in the oscillating field individual,it indicates the competition between processes of dynamically assisted Schwinger mechanism and pure photon absorbtion.

4 Conclusion and Discussion

In the frame of computational simulation for the pair production process we introduce a simple but useful physical quantity,conversion energy as the sum of the electron’s and its conjugate positron’s mass-energy.We demonstrated that the conversion energy can not only reveal the pair production characteristics but also give the yields of each production channel.We investigated the contribution of different production mechanisms to the final yields in the pair production process.

We detected a signature of the e ff ective mass and found an inconsistent temporal behaviour among each order of photon absorbtion in an oscillating field.We investigated the composition of production channels in a bifrequent field and demonstrated that the multiphoton process can be triggered by the combination of same photons as well as different photons.We investigated the distribution of final yields in each production channel in a combined field and demonstrated that dynamically assisted Schwinger mechanism is essential to the enhancement of production rate.We also demonstrated a competition behaviour of different production channels.It is possible to conduct more qualitative investigations on the feature of individual production channels in the term of conversion energy in the future work.

Acknowledgments

We enjoyed several helpful discussions with Suo Tang,and Feng Wan.Authors are also grateful to the anonymous referee for the helpful comments and suggestions.

References

[1]J.S.Schwinger,Phys.Rev.82(1951)664.

[2]F.Sauter,Z.Phys.69(1931)742.

[3]W.Heisenberg and H.Euler,Z.Phys.98(1936)714.

[4]http://www.eli-beams.eu/.

[5]E.Brezin and C.Itzykson,Phys.Rev.D 2(1970)1191.

[6]V.S.Popov,JETP Lett.13(1971)185.

[7]R.Alkofer,M.B.Hecht,C.D.Roberts,S.M.Schmidt,and D.V.Vinnik,Phys.Rev.Lett.87(2001)193902.

[8]R.G.Newton,Phys.Rev.96(1954)523.

[9]W.Y.Tsai and A.Yildiz,Phys.Rev.D 8(1973)3446.

[10]V.N.Baier,V.M.Katkov,and V.M.Strakhovenko,Sov.Phys.JETP 40(1974)225.

[11]S.P.Kim and D.N.Page,Phys.Rev.D 65(2002)105002.[12]G.V.Dunne and C.Schubert,Phys.Rev.D 72(2005)105004.

[13]G.V.Dunne,Q.H.Wang,H.Gies,and C.Schubert,Phys.Rev.D 73(2006)065028.

[14]Andr´e D.Bandrauk,and Hai Shen,J.Chem.Phys.99(1993)1185.

[15]T.Cheng,Q.Su,and R.Grobe,Cont.Phys.51(2010)315.

[16]P.Krekora,K.Cooley,Q.Su,and R.Grobe,Phys.Rev.Lett.95(2005)070403.

[17]Y.Liu,M.Jiang,Q.Z.Lv,Y.T.Li,R.Grobe,and Q.Su,Phys.Rev.A 89(2014)012127.

[18]Q.Z.Lv,Y.Liu,Y.J.Li,R.Grobe,and Q.Su,Phys.Rev.Lett.111(2013)183204.

[19]Y.Liu,Q.Z.Lv,Y.T.Li,R.Grobe,and Q.Su,Phys.Rev.A 91(2015)052123.

[20]M.Jiang,Q.Z.Lv,Z.M.Sheng,R.Grobe,and Q.Su,Phys.Rev.A 87(2013)042503.

[21]M.Jiang,W.Su,Z.Q.Lv,X.Lu,Y.J.Li,R.Grobe,and Q.Su,Phys.Rev.A 85(2012)033408.

[22]Suo Tang,Bai-Song Xie,Ding Lu,Hong-Yu Wang,Li-Bin Fu,and Jie Liu,Phys.Rev.A 88(2013)012106.

[23]Fran¸cois Gelis and Naoto Tanji,Phys.Rev.D 87(2013)125035.

[24]F.Hebenstreit,J.Berges,and D.Gelfand,Phys.Rev.D 87(2013)105006.

[25]R.Alkofer,etal.,Phys.Rev.Lett.87(2001)193902.

[26]C.D.Roberts,S.M.Schmidt,and D.V.Vinnik,Phys.Rev.Lett.89(2002)153901.

[27]F.Hebenstreit,R.Alkofer,G.V.Dunne,and H.Gies,Phys.Rev.Lett.102(2009)150404.

[28]A.Nuriman,B.S.Xie,Z.L.Li,and D.Sayipjamal,Phys.Lett.B 717(2012)465.

[29]A.Nuriman,Z.L.Li,and B.S.Xie,Phys.Lett.B 726(2013)820.

[30]M.Orthaber,F.Hebenstreit,and R.Alkofer,Phys.Lett.B 698(2011)80.

[31]W.Y.Wu,F.He,R.Grobe,and Q.Su,J.Opt.Soc.Am.B 32(2015)2009.

[32]I.Akal,S.Villalba-Ch´avez,and C.M¨uller,Phys.Rev.D 90(2004)113004.

[33]Martin J.A.Jansen and Carsten M¨uller,Phys.Rev.A 88(2013)052125.

[34]A.Otto,D.Seipt,D.Blaschke,S.A.Smolyansky,and B.K¨ampfer,Phys.Rev.D 91(2015)105018.

[35]R.Sch¨utzhold,H.Gies,and G.Dunne,Phys.Rev.Lett.101(2008)130404.

[36]G.V.Dunne,H.Gies,and R.Sch¨utzhold,Phys.Rev.D 80(2009)11130.

[37]A.Ottoa,D.Seiptc,D.Blaschked,B.K¨ampfera,and S.A.Smolyanskye,Phys.Lett.B 740(2012)335.

[38]Robert Dabrowski and Gerald V.Dunne,Phys.Rev.D 90(2014)025021.

[39]T.Heinzl,A.Ilderton,and M.Marklund,Phys.Lett.B 692(2010)250.

[40]Christian Kohlf¨urst,Holger Gies,and Reinhard Alkofer,Phys.Rev.Lett.112(2014)050402.