Laser Polarization E ff ect on Molecular Harmonic and Elliptically Polarized Attosecond Pulse Generation∗
2017-05-18LiQiangFeng冯立强WenLiangLi李文亮andHangLiu刘航
Li-Qiang Feng(冯立强),Wen-Liang Li(李文亮),and Hang Liu(刘航)
1College of Science,Liaoning University of Technology,Jinzhou 121001,China
2State Key Laboratory of Molecular Reaction Dynamics,Dalian Institute of Chemical Physics Chinese Academy of Sciences,Dalian 116023,China
3School of Chemical and Environmental Engineering,Liaoning University of Technology,Jinzhou 121001,China
4Key Laboratory at Universities of Education Department of Xinjiang Uygur Autonomous Region for New Energy Materials,Xinjiang Institute of Engineering,Urumqi 830091,China
1 Introduction
High-order harmonic generation(HHG)as one of the most important intense laser-matter physics has been widely investigated owing to its potential of producing ultrashort EUV and X-ray attosecond pulses.[1−8]The HHG process from atom and symmetrical molecule(e.g.H+2)can be explained through the recollision model[9]with the steps of ionization,acceleration and recombination.In detail,(i)an electron is first released into continuum by tunneling ionization.(ii)Once free,it oscillates and gains kinetic energy in the continuum in response to the laser field.(iii)Finally,the ionized electron may recombine with the parent ions and emit a harmonic with the energy up to Ip+3.17Upfor the single-color field,where Ipis the ionization potential and Up=Ilaser/4ω2is the ponderomotive energy of the electron.
The most important application for atomic harmonics is to produce the linearly polarized attosecond pulses with higher photon energy(e.g.the X-ray region).Therefore,many schemes have been paid to extend the harmonic cuto ff,such as the ionization gating method,[10−12]the polarization gating scheme,[13−17]the attosecond lighthouse,[18−19]the non-collinear harmonic generation,[20−21]the two-color or multi-color controlling field scheme,[22−24]the mid-infrared field controlling scheme,[25−27]the unipolar pulse assisted harmonic extension,[28−30]the chirp pulse controlling scheme,[31−33]and the spatially inhomogeneous field e ff ect,[34−39]etc.However,as we know,when the atom is exposed to the circularly polarized lasers,no circularly or elliptically polarized harmonics can be generated because of the conservation of angular momentum and the suppression of the recollision.
Molecular harmonics show a more complicated structure in comparison with the atomic harmonics,such as the extended harmonic cuto ffcaused by the multi-channel harmonic emission[40]and the resonant peaks caused by the laser induced electron transfer[41]etc.Most impor-tantly,due to the non-spherical geometry of molecules,the restrictions of the conservation of angular momentum and the recombination for atomic system are avoided,rendering molecules ideal candidates for the generations of the elliptically and the circularly polarized harmonics and attosecond pulses.[42]For instance,Yuan and Bandrauk[43−46]theoretically investigated the generation of the circularly or elliptically polarized harmonics and obtained an isolated circularly polarized attosecond pulse with the combination of a few cycle elliptically polarized laser pulse and a terahertz field.[47]Miloˇsevi´c,etal.[48]investigated the generation of circularly polarized harmonics by using a bichromatic circularly polarized laser pulse with the opposite rotation polarization directions.So far,by using a linearly polarized laser pulse,the elliptically polarized harmonics have also been experimentally and theoretically produced for aligned,N2and CO2molecules.[49−53]
However,the durations of the produced circularly or elliptically polarized pulses are still signi ficantly longer than 1 atomic unit of time(the atomic unit of time is 24as)and the photon energies mainly cover in the EUV region.Therefore,in this paper,we theoretically investigate the molecular harmonics fromdriven by the linearly polarized laser pulses with different orientation angles.Firstly,the below and above-threshold harmonics show the resonant enhanced peak around the 7th harmonic and many maxima and minima,respectively.Moreover,a series of anomalous elliptically polarized harmonics can be obtained with the introduction of the polarized angle.Secondly,with the introduction of the spatial inhomogeneous e ff ect(which is a current hot issue on harmonics and attosecond pulses generations[34−39,54]),the harmonic cuto ff s are extended,and the harmonic modulations are reduced.Most importantly,the ellipticities of the harmonics become stable with the values from ε=0.1 to ε=0.3.As a result,four supercontinua with the bandwidths of 407 eV,310 eV,389 eV and 581 eV can be obtained.Finally,by Fourier transforming the harmonics,a series of sub-25as elliptically polarized attosecond X-ray pulses with elliptically from 0.1 to 0.3 can be obtained.
2 Method
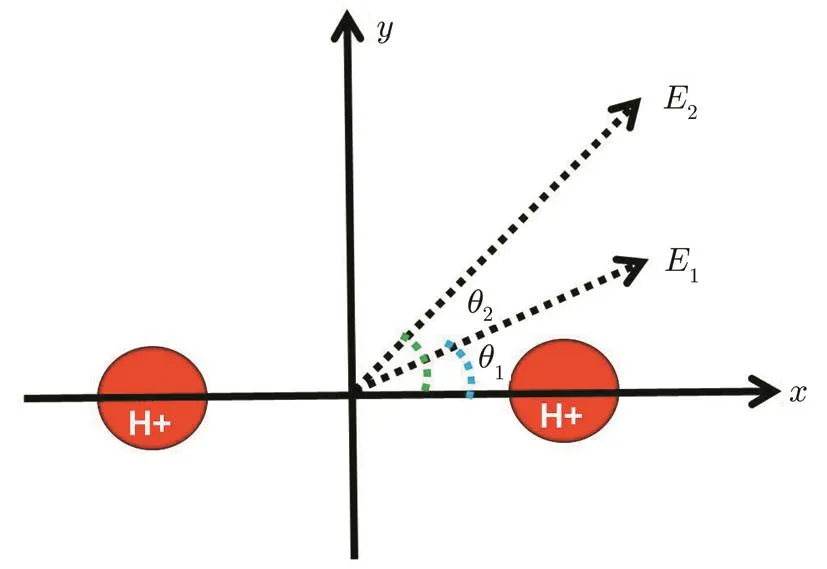
Fig.1 The geometry of the and molecular axis is along the x axis,which forms the angles θ1and θ2with the directions of the laser fields.
The molecular harmonic spectra and the attosecond pulse generations are explored on the basis of the single active electron approximation by numerically solving the two-dimensional time-dependent Schr¨odinger equation(2D-TDSE),[55]
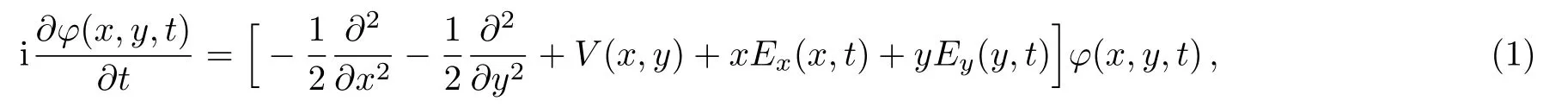
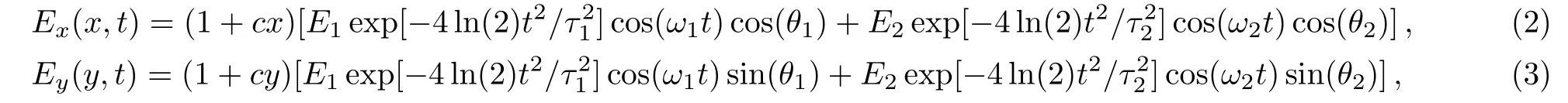
whereEi,ωiand τi(i=1,2)are the amplitudes,the frequencies and the pulse durations of the two input pulses. θ1,2are the angles between the directions of the laser pulses and the molecular axis(x),as shown in Fig.1.c is the spatial inhomogeneous parameter.The initial wave function φinitial(x,y,t)is constructed by the imaginary time-propagation method and the time dependent wave function φ(x,y,t)can be propagated by using the standard second-order splitoperator method.[56−59]
Once the time dependent wave function is determined,the dipole acceleration can be expressed as,[60]

HHG spectra can be obtained by Fourier transforming the time-dependent dipole acceleration,

The ellipticities ε of the harmonics can be expressed as,[61]
国家防总副总指挥、水利部部长陈雷就贯彻落实回良玉副总理讲话及会议精神提出三点要求:第一,深刻领会回良玉副总理重要讲话精神,统一思想,提高认识,切实增强使命感责任感;第二,紧紧围绕今年防汛抗旱目标任务,突出重点,抓住关键,最大程度减轻灾害损失;第三,立足防大汛抗大旱抢大险救大灾,超前谋划,周密部署,确保各项措施落实到位。
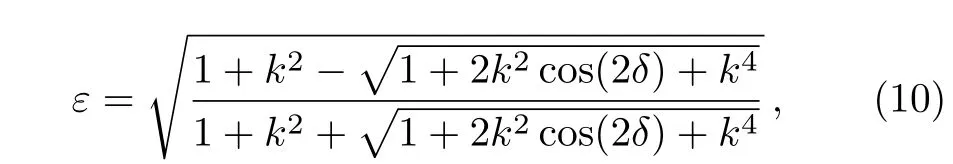
where,k=and δ=arg[ay(ω)]−arg[ax(ω)]are the amplitude ratio and the phase di ff erence of the two components,respectively.The linearly,elliptically and circularly polarized harmonics or pulses correspond to ε =0,0< ε <1 and ε =1,respectively.
Time-frequency analyses of the harmonic generation can be obtained by means of the wavelet transformation of the dipole acceleration dA(t),[62]
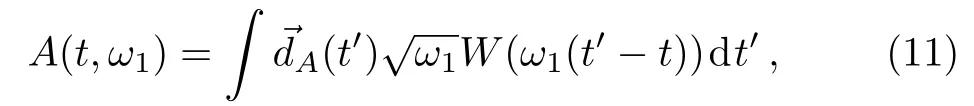
where W(x)=is the Morlet wavelet with the wavelet window function fixed at ξ=20 in this paper.
Temporal pro fi le of the attosecond pulse can be generated through the Fourier transformation of the spectral continuum,

where q means the order of the harmonics.
3 Results and Discussion
3.1 Below-Threshold Molecular Harmonic Characteristic
Figure 2(a)shows the below-threshold(the harmonic energies/orders are lower than the ionization potential of)molecular harmonic yields versus the single-color polarized angle θ1.The laser field is 5 fs/800 nm spatial homogeneous pulse(c=0.0)with I1=1.0×1015W/cm2.For the equilibrium internuclear distance(R=2 a.u.),the ionization potential ofis−29.9 eV,thus the belowthreshold harmonics span the range of H3(4.65 eV)to H17(26.35 eV)orders.As one can see,most of below-threshold harmonics exhibit the anomalous radiation intensities,but there is one visible enhanced peak around the H7 order.Figure 2(b)shows the part of the HHG spectra fromdriven by the single linearly polarized pulse(θ1=0.0π)with different internuclear distances.The harmonic yields have been multiplied by factors of 1,10−3,and 10−6from top to bottom for the purpose of clarity.We see that the visible resonant enhanced peak around the H7 order will move toward to the lower harmonic order(even disappearance)with the increase of internuclear distance.As we know that the excited state plays an important role in molecular harmonic generation.[42,63−65]Thus,through analyzing the energies of the ground state(GS)and the 1st excited state(ES)of(that is 30 eV and 18 eV at R=2.0 a.u.),we see that the location of the H7 order is equal to the di ff erence between the GS and the 1st ES.Moreover,the energies of these two states become nearly degenerate at larger R(i.e.17.6 eV and 17.4 eV at R=7.0 a.u.),which agrees well with the above red-shift(even disappeared)resonant peak.Thus,we believe that this enhanced peak is caused by the laser-induced electron transfer between the GS and the 1st ES.
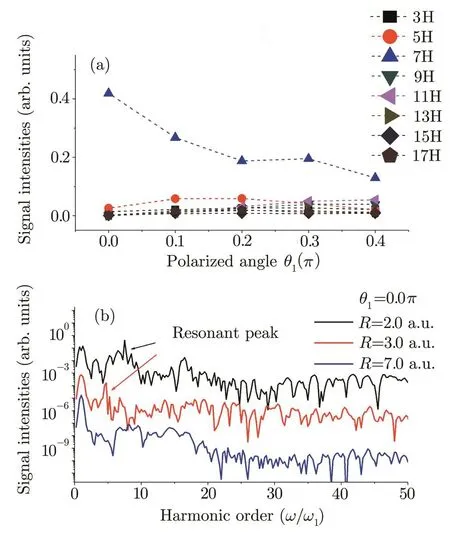
Fig.2 (a)The intensities of the below-threshold molecular harmonics scaling with the polarized angle θ1.The laser field is 5 fs/800 nm spatial homogeneous pulse(c=0.0)with I1=1.0×1015W/cm2.The internuclear distance is chosen to be R=2.0 a.u.(b)Part of the harmonic spectra driven by the above field with θ1=0.0π and R=2.0 a.u.,3.0 a.u.,7.0 a.u.The harmonic yields have been multiplied by factors of 1,10−3,and 10−6from top to bottom for the purpose of clarity.
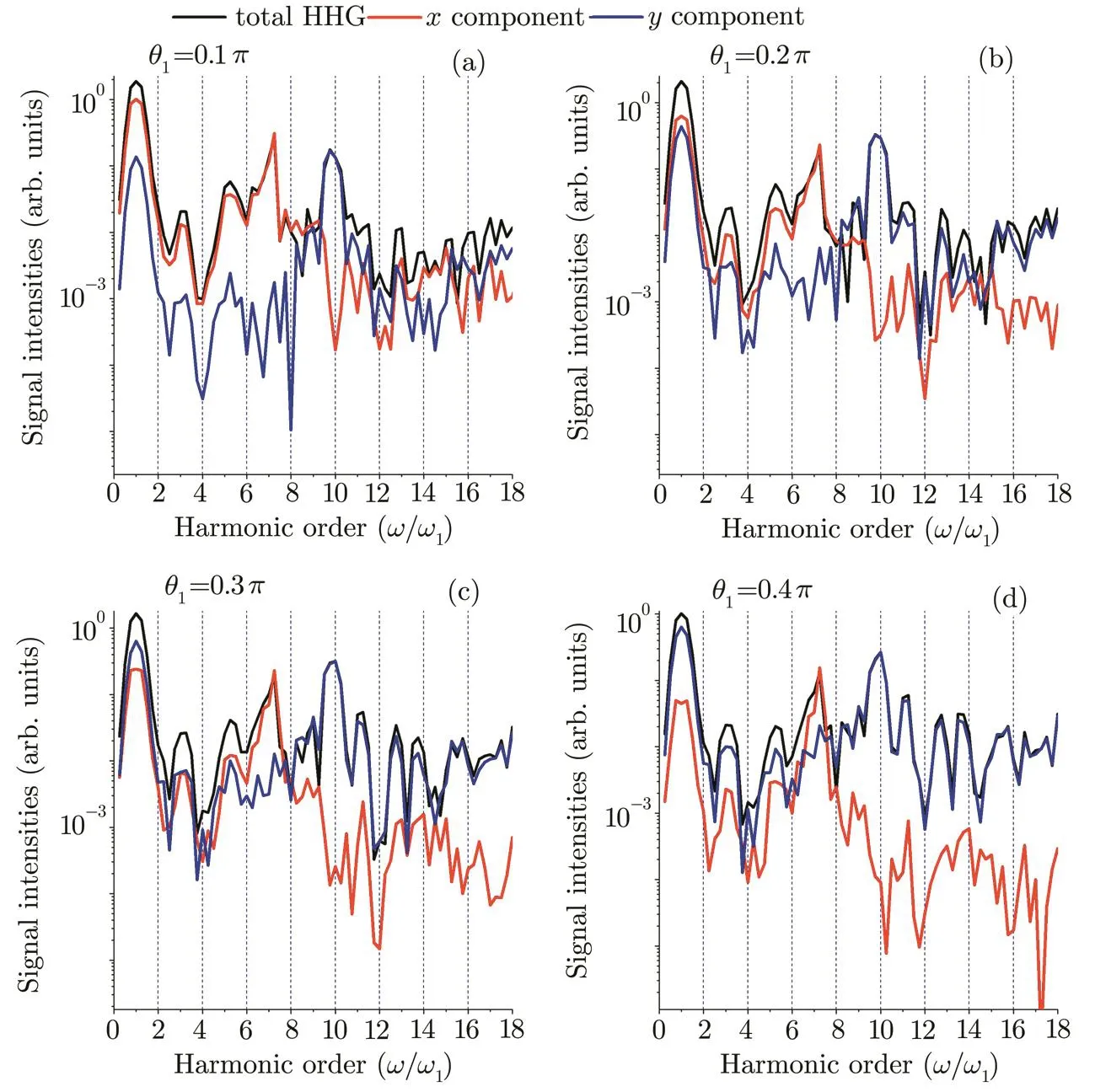
Fig.3 Below-threshold molecular harmonics and their components in x and y directions for the cases of the single linearly polarized pulses with(a) θ1=0.1π;(b) θ1=0.2π;(c) θ1=0.3π;(d) θ1=0.4π.
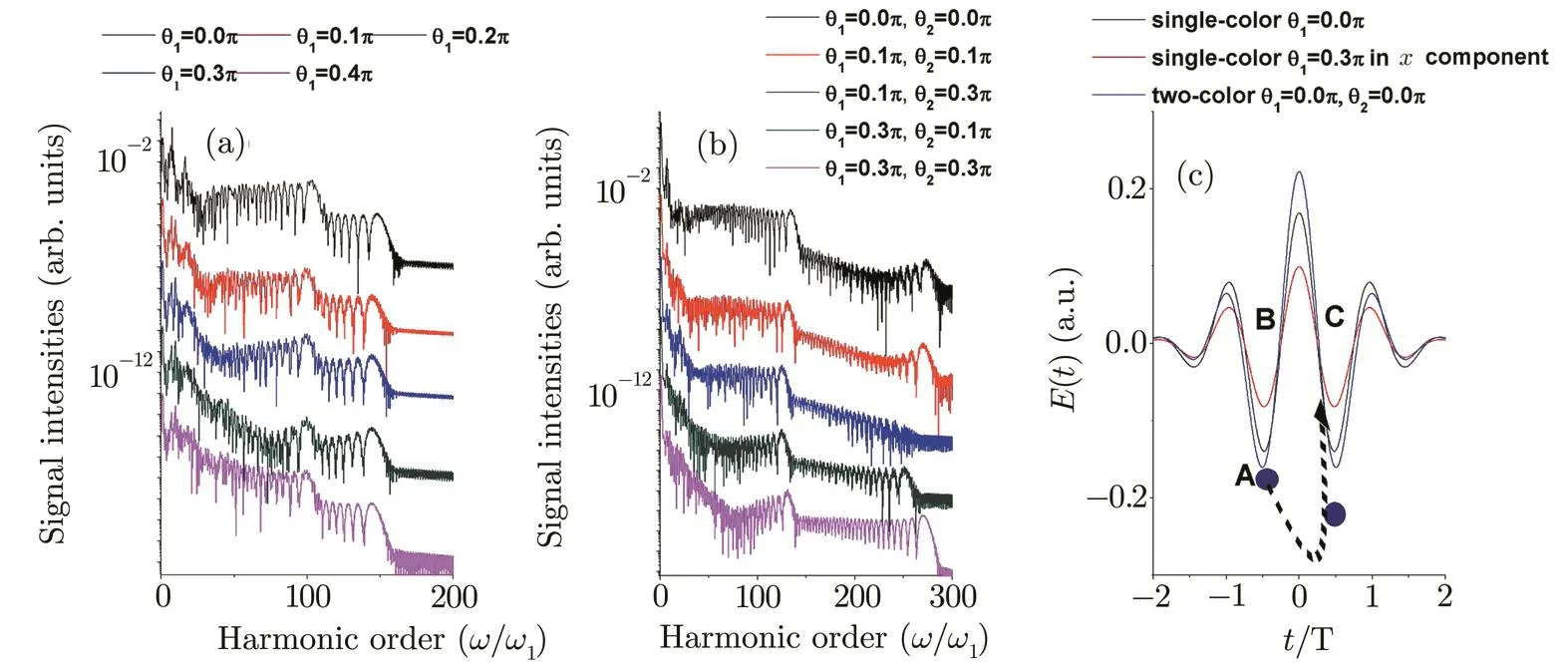
Fig.4 (a)Above-threshold molecular harmonics driven by the single linearly polarized pulses with θ1=0.0π–0.4π.(b)Above-threshold molecular harmonics driven by the two-color linearly polarized pulses with θ1=0.1π, θ2=0.1π;θ1=0.1π,θ2=0.3π;θ1=0.3π,θ2=0.1π;θ1=0.3π,θ2=0.3π.The second controlling pulse is 10 fs/1200 nm spatial homogeneous pulse(c=0.0)with I2=1.0×1014W/cm2.The harmonic yields have been multiplied by factors of 1,10−3,10−6,and so on from top to bottom for the purpose of clarity.(c)Laser pro fi les of the single linearly polarized pulses with θ1=0.0π (case I), θ1=0.3π in x direction(case II)and two-color linearly polarized pulses with θ1= θ2=0.0π(case III).T means the optical cycle of 800 nm field.
3.2 Above-threshold Molecular Harmonic Characteristic
Figure 4(a)shows the above-threshold(the harmonic energies/orders are larger than the ionization potential of)molecular harmonics driven by the single linearly polarized pulses with θ1=0.0π–0.4π.Clearly,the harmonic spectra reveal two harmonic plateaus,and the maximum harmonic cuto ff s are decreased with the increase of the polarized angle θ1(i.e.Ecutoff(θ1=0.0π)=147ω1;Ecutoff(θ1=0.1π)=145ω1;Ecutoff(θ1=0.3π)=143ω1).Moreover,the harmonics exhibit many minima.This is because that the electron can experience the recombination with two nucleus,which means the contributions to the recombination amplitude from both nuclei are added coherently,thus giving rise to the interference structure in the harmonic spectra,which is called as the two-center interference.[66−68]Here,one can obtain the interference minima or maxima by using the recombination model,[69−70]
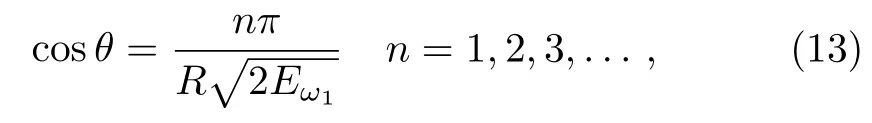
whereEω1is the emitted harmonic energy(here we assume all the kinetic energy of the electron is transformed into the harmonic emission during the recombination),and θ is the angle between the laser polarization and the molecular axis.The calculated results are shown in Table 1.As seen in Table 1,for the present paper,n=1,3,5,...in Eq.(13)correspond to the minima,and n=2,4,6,...in Eq.(12)correspond to the maxima.For instance,for θ1=0.0π–0.4π cases,(i)the minima for n=1,3 are respective 22ω1,198ω1(for θ1=0.0π);24ω1,219ω1(for θ1=0.1π);33ω1,302 ω1(for θ1=0.2π);63ω1,573ω1(for θ1=0.3π);and 230ω1,2076ω1(for θ1=0.4π).(ii)The maxima for n=2,4 are respective 88ω1,352ω1(for θ1=0.0π);97ω1,389ω1(for θ1=0.1π);134ω1,538ω1(for θ1=0.2π);255ω1,1020ω1(for θ1=0.3π);and 922ω1,3691ω1(for θ1=0.4π).We note that the minima or the maxima harmonics obtained from Eq.(13)for the larger polarized angles and higher number n are too high to observe in the present laser intensity.Moreover,as we know that the positions of the maxima are hardly to see.Therefore,we only choose the smaller polarized angles(θ1=0.0π–0.3π)with n=1 to analyze the minima in the harmonic spectra.Clearly,we see that the predictions of the minima shown in Table 1 are in fair agreement with our quantum calculations shown in Fig.4(a).And a blueshift of these points can be found with the increase of the polarized angle.Figure 4(b)shows the above-threshold molecular harmonics driven by the two-color linearly polarized pulses with different polarized angles.The second controlling pulse is 10 fs/1200 nm spatial homogeneous pulse(c=0.0)with I2=1.0×1014W/cm2.It shows that with the introduction of the second controlling pulse,the harmonic cuto ff s are extended and the maxima and the minima can also be found on the harmonics but with an energy shift.For instance,(i)for θ1=0.1π,θ2=0.1π case,the 1st minima is around the 24ω1,which agrees well with the single polarized pulse case(θ1=0.1π).However,with the increase of the second polarized angle at θ1=0.1π, θ2=0.3π,a blue-shift of the 1st minima has been obtained around the 28ω1.(ii)For θ1=0.3π,θ2=0.3π case,the minima around the 66ω1can be obtained as same as that generated from the single polarized pulse with θ1=0.3π.But,with the decrease of the second polarized angle at θ1=0.3π,θ2=0.1π,the minima with the red-shift around the 41ω1can be found.Figure 4(c)shows the laser pro fi les of the single linearly polarized pulses with θ1=0.0π (case I), θ1=0.3π in x direction(case II)and two-color linearly polarized pulses with θ1= θ2=0.0π (case III).According to the recollision model,[9]the ionization of the electron occurs near the amplitude of the laser(such as A point).Further,the acceleration and the recombination of the ionized electron can be achieved during the later half optical cycle(such as the B-C process).Finally,it can recombine with its parent ion emitting a photon as the harmonic radiation energy.Through analyzing the laser pro fi les shown in Fig.4(c),the envelopes of the A-B-C amplitudes are respectively decreased(case II)or increased(case III)as the polarized angle θ1increased or with the introduction of the second controlling pulse,thus,the free electron will obtain and release less(case II)or more(case III)energies in its accelerating and returning process,which is responsible for the decrease and extension of the harmonic cuto ff s shown in Figs.4(a)and 4(b).

Table 1 Minima or maxima of the harmonics at different polarized angles calculated from Eq.(13).The internuclear distance is chosen to be R=2.0 a.u.

Fig.5 Time-frequency analyses of the harmonic generation for the cases of the single-color polarized pulses with(a)θ1=0.1π;(b) θ1=0.2π;(c) θ1=0.3π;(d) θ1=0.4π.

Fig.6 Time-frequency analyses of the harmonic generation for the cases of the two-color linearly polarized pulses with(a) θ1=0.1π,θ2=0.1π;(b) θ1=0.1π,θ2=0.3π;(c) θ1=0.3π,θ2=0.1π;(d) θ1=0.3π,θ2=0.3π.
Figures 5(a)–5(d)depict the time-frequency analyses of the harmonic generation for the cases of the single linearly polarized pulses with θ1=0.1π–0.4π.We see that for the present short pulses,there are three main harmonic emission events,and the emission energies can be separated to two parts.Particularly,one is lower than 100ω1with the contributions from all the three harmonic emission events,and the other one is higher than 100ω1with the contribution only from the 2nd harmonic emission event,which is the reason behind the two harmonic plateaus shown in Fig.4(a).Moreover,each peak receives two similar contributions from the left(short trajectory)and the right(long trajectory)trajectories,thus,leading to the larger modulations on the harmonic spectra.[71]Figures 6(a)–6(d)depict the time pro fi les of the harmonic generations for the cases of the two-color polarized pulses with θ1=0.1π, θ2=0.1π; θ1=0.1π, θ2=0.3π;θ1=0.3π,θ2=0.1π;θ1=0.3π,θ2=0.3π,respectively.It shows that with the help of the second controlling pulse,three main harmonic emission events can be found during the harmonic emission process,and the intensities of the 2nd and the 3rd harmonic emission events are much higher than that of the 1st one,which is responsible for the observed two-plateau structure on the HHG.Moreover,the maximum recombination energy is extended in comparison with the single color cases,which agrees well with the quantum results shown in Fig.4(b).But each emission events also receives two similar contributions from the short and the long trajectories,which is unbene ficial to isolated attosecond pulse generation.
3.3 Elliptically Polarized Harmonic and Attosecond Pulse Generations
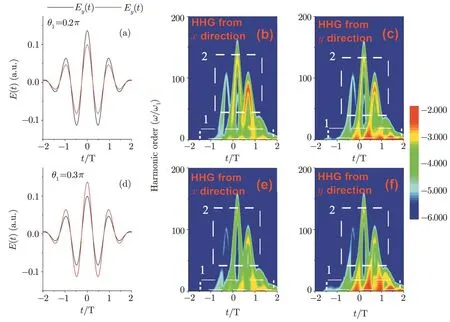
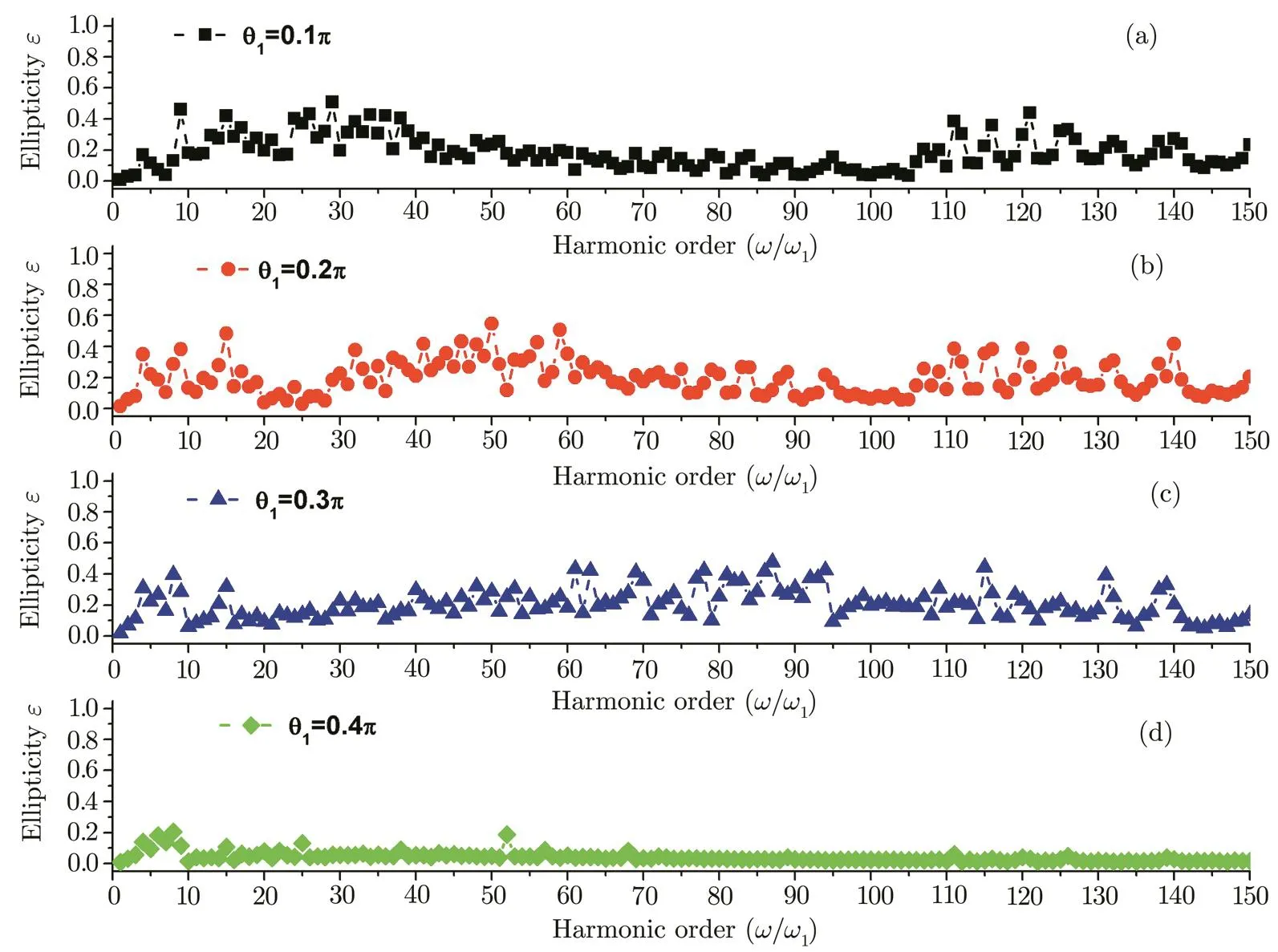
Figures 7(a)–7(d)show the above-threshold molecular harmonics and their components in x and y directions for the cases of the single linearly polarized pulses with θ1=0.1π–0.4π,respectively.It shows that for the smaller polarized angles θ1=0.1π,as shown in Fig.7(a),the harmonic intensities from the y component are higher than those from the x component in the lower harmonic orders(H9 Fig.7 Above-threshold molecular harmonics and their components in x and y directions for the cases of the single linearly polarized pulses with(a) θ1=0.1π;(b) θ1=0.2π;(c) θ1=0.3π;(d) θ1=0.4π. In order to understand the harmonic distributions in the x and the y components,in Fig.8,we present the laser pro fi les and the time-frequency analyses of the harmonic spectra in the x and the y components for the cases of the single linearly polarized pulses with θ1=0.2π and 0.3π(here we use this two cases as the example to explain the harmonic distributions in the x and the y components).Firstly,the intensities of laser pro fi les in the x or the y component are higher than that in the y or the x component(see Figs.8(a)and 8(d))for the cases of θ1=0.2π and θ1=0.3π,respectively.Thus,the harmonic emission from the x or the y component should respectively present the main role in harmonic generation,which is in agreement with the calculated harmonic spectra shown in Fig.7.In detail,through analyzing the time-frequency analyses of the harmonic spectra,we see that for the case of θ1=0.2π (see Figs.8(b)and 8(c)),the intensities of the three harmonic emission events from the y component are higher than those from the x component for the lower harmonic orders(dashed white frame 1);while for the higher harmonic orders(dashed white frame 2),the intensities of the three harmonic events from the x component are higher than those from the y component,which is responsible for the asymmetric harmonic distributions in the x and the y components.For the case of θ1=0.3π(see Figs.8(e)and 8(f)),due to the amplitude of the laser field in the y component is enhanced,the intensities of the three harmonic emission events from the y component play the main role in all harmonic orders,thus resulting in the remarkable enhancement of the harmonic intensity in the y component. Fig.8 Laser pro fi les in the x and the y components for the cases of(a) θ1=0.2π;(d) θ1=0.3π.Time-frequency analyses of the harmonic generation in the x and the y components for the cases of(b)and(c) θ1=0.2π;(e)and(f)θ1=0.3π. Figures 9(a)–9(d)show the above-threshold molecular harmonics and their components in the x and the y directions for the cases of the two-color linearly polarized pulses with θ1=0.1π,θ2=0.1π; θ1=0.1π,θ2=0.3π;θ1=0.3π, θ2=0.1π; θ1=0.3π, θ2=0.3π.Clearly,the fundamental field plays an important role in harmonic yields.For instance,for θ1=0.1π two cases,shown in Figs.9(a)and 9(b),the dominating harmonics still come from the x component.For θ1=0.3π two cases,shown in Figs.9(c)and 9(d),we see that with the increase of the fundamental polarized angles θ1,the contribution of the y component is enhanced(Fig.9(c)),and with the further increase of the controlling polarized angles θ2,the contribution of the y component is higher than that of the x component(Fig.9(d)).The reasons for the harmonic distributions in the two-color field are similar as those from the single-color field.Thus,we do not show in this paper. As we know that the ellipticities of the harmonics are determined by the amplitude ratio and the phase di ff erence of the two components,thus,according to Eq.(10),we calculated the ellipticities of the harmonics for the cases of the single-color and two-color polarized pulses as shown in Figs.10 and 11,respectively.Firstly,for the cases of the single linearly polarized pulses with θ1=0.1π,0.2π,and 0.3π,shown in Figs.10(a)–10(c),although the ellipticities of harmonics are complicated,some nearstable elliptically polarized harmonics from 50ω1to 100ω1with ε=0.1 for θ1=0.1π case,from 70ω1to 90ω1with ε=0.2 for θ1=0.2π case,from 20ω1to 50ω1with ε=0.15 for θ1=0.3π case can be found.However,for the case of the single linearly polarized pulse with θ1=0.4π,shown in Fig.10(d),we see that the ellipticities of harmonics are nearly zero,corresponding to the linearly polarized harmonics.For the cases of the two-color polarized pulses with θ1=0.1π,θ2=0.1π and θ1=0.1π,θ2=0.3π,shown in Figs.11(a)and 11(b),the near-stable elliptically polarized harmonics have been broadened,and two elliptically polarized harmonic plateaus from 60ω1to 140ω1with ε=0.1 and from 150ω1to 200ω1with ε=0.15 can be obtained.While for the cases of the two-color polarized pulses with θ1=0.3π,θ2=0.1π and θ1=0.3π,θ2=0.3π,shown in Figs.11(c)and 11(d),there is only one nearstable elliptically polarized harmonic plateau from 150ω1to 200ω1with ε=0.2. Fig.9 Above-threshold molecular harmonics and their components in x and y directions for the cases of two-color linearly polarized pulses with(a) θ1=0.1π,θ2=0.1π;(b) θ1=0.1π,θ2=0.3π;(c) θ1=0.3π,θ2=0.1π;(d) θ1=0.3π,θ2=0.3π. From the above analyses,we see that although the near-stable elliptically polarized harmonics can be generated by using the present linearly polarized pulses,the larger modulations on the harmonics are unbene ficial to the generation of the isolated elliptically polarized attosecond pulse.Thus,in the following discussion,we try to obtain the near-stable elliptically polarized harmonics with less modulation. Figures 12(a)–12(d)show the molecular HHG spectra driven by the above four two-color polarized pulses with different spatial inhomogeneous parameters.Clearly,by properly choosing the spatial inhomogeneous parameters,e.g.c=0.004 for θ1=0.1π,θ2=0.1π case(Fig.12(a));c=0.001 for θ1=0.1π, θ2=0.3π case(Fig.12(b));c=0.002 for θ1=0.3π,θ2=0.1π case(Fig.12(c));and c=0.002 for θ1=0.3π,θ2=0.3π case(Fig.12(d)),not only the harmonic cuto ff s are extended,but also the harmonic modulations are reduced in comparison with the spatial homogeneous field cases.As a result,four supercontinua with the bandwidths of 407 eV,310 eV,389 eV,and 581 eV can be obtained. Figures 13(a)–13(d)depict the ellipticities of the harmonics for the cases of the above four spatial inhomogeneous combined fields.Particularly,(i)for the case of θ1=0.1π, θ2=0.1π,c=0.004,shown in Fig.13(a),a near-stable elliptically polarized harmonic bandwidth with ε=0.1 can be found from the 100ω1to the 200ω1.(ii)For the case of θ1=0.1π, θ2=0.3π,c=0.001,shown in Fig.13(b),a near-stable elliptically polarized harmonic bandwidth with ε=0.3 can be found from the 125ω1to the 175ω1.(iii)For the case of θ1=0.3π,θ2=0.1π,c=0.002,shown in Fig.13(c),a near-stable elliptically polarized harmonic bandwidth with ε=0.3 can be found from the 125ω1to the 225ω1.(iv)For the case of θ1=0.3π, θ2=0.3π,c=0.002,shown in Fig.13(d),a near-stable elliptically polarized harmonic bandwidth with ε=0.3 can be found from the 150ω1to the 250ω1. Fig.10 Ellipticities of the harmonics for the cases of the single-color polarized pulses with(a)θ1=0.1π;(b)θ1=0.2π;(c) θ1=0.3π;(d) θ1=0.4π. Fig.11 Ellipticities of the harmonics for the cases of the two-color linearly polarized pulses with(a) θ1=0.1π,θ2=0.1π;(b) θ1=0.1π,θ2=0.3π;(c) θ1=0.3π,θ2=0.1π;(d) θ1=0.3π,θ2=0.3π. Fig.12 Molecular HHG spectra driven by the spatial inhomogeneous two-color polarized pulses with(a) θ1=0.1π,θ2=0.1π,c=0.004;(b) θ1=0.1π,θ2=0.3π,c=0.001;(c) θ1=0.3π,θ2=0.1π,c=0.002;(d) θ1=0.3π,θ2=0.3π,c=0.002.For comparison,the HHG spectra from the corresponding homogeneous fields have also been shown. Fig.13 Ellipticities of the harmonics for the cases of the spatial inhomogeneous two-color linearly polarized pulses with(a) θ1=0.1π,θ2=0.1π,c=0.004;(b) θ1=0.1π,θ2=0.3π,c=0.001;(c) θ1=0.3π,θ2=0.1π,c=0.002;(d)θ1=0.3π,θ2=0.3π,c=0.002. Fig.14 Time-frequency analyses of the harmonic generation for the cases of the spatial inhomogeneous two-color linearly polarized pulses with(a) θ1=0.1π,θ2=0.1π,c=0.004;(b) θ1=0.1π,θ2=0.3π,c=0.001;(c) θ1=0.3π,θ2=0.1π,c=0.002;(d) θ1=0.3π,θ2=0.3π,c=0.002. Fig.15 Temporal pro fi les of attosecond pulses superposing the harmonics of(a)the θ1=0.1π,θ2=0.1π,c=0.004 case from the 100ω1to the 200ω1orders;(b)the θ1=0.1π, θ2=0.3π,c=0.001 case from the 125ω1to the 175ω1 orders;(c)the θ1=0.3π,θ2=0.1π,c=0.002 case from the 125ω1to the 175ω1orders,from the 175ω1to the 225ω1 orders;(d)the θ1=0.3π,θ2=0.3π,c=0.002 case from the 150ω1to the 200ω1orders,from the 200ω1to the 250ω1 orders. Figures 14(a)–14(d)show the time-frequency analyses of the harmonic generation driven by the above four spatial inhomogeneous combined fields.We see that with the introduction of the spatial inhomogeneous e ff ect,the maximum recombination energies from the harmonic emission events are enhanced,and the single quantum trajectory is selected to contribute to the harmonic spectra,which is bene ficial to the isolated attosecond production.Particularly,(i)for the case of θ1=0.1π,θ2=0.1π,c=0.004,shown in Fig.14(a),the harmonic energies from the 100ω1to the 250ω1are contributed by the single short quantum trajectory.(ii)For the case of θ1=0.1π, θ2=0.3π,c=0.001,shown in Fig.14(b),the contribution of the short quantum trajectory is higher than that of the long quantum trajectory when the harmonics generated from the 100ω1to the 200ω1.(iii)For the case of θ1=0.3π,θ2=0.1π,c=0.002,shown in Fig.14(c),the maximum harmonic energies from the 100ω1to the 350ω1are contributed by the short quantum trajectory.(iv)For the case of θ1=0.3π, θ2=0.3π,c=0.002,shown in Fig.14(d),the single short quantum trajectory has been well selected to contributed to the maximum harmonic emission event. Figure 15 shows the elliptically polarized attosecond pulses generations through the Fourier transformation of the above harmonic spectra.Firstly,through analyzing the ellipticities and the time pro fi les of the harmonics shown in Figs.13 and 14,we see that due to the oscillation of the ellipticities and the interference modulations caused by the two quantum trajectories,the selection of an entire supercontinuum region cannot provides the possible situation for generating the near-stable elliptically polarized isolated attosecond pulse.Therefore,superposing part of the harmonics with the near-stable ellipticities and the single trajectory contribution is much better for the production of the elliptically polarized isolated attosecond pulse.Thus,according to the results in Figs.13 and 14,by superposing the harmonics of(i)the θ1=0.1π,θ2=0.1π,c=0.004 case from the 100ω1to the 200ω1orders;(ii)the θ1=0.1π, θ2=0.3π,c=0.001 case from the 125ω1to the 175ω1orders;(iii)the θ1=0.3π,θ2=0.1π,c=0.002 case from the 125ω1to the 175ω1orders,from the 175ω1to the 225ω1orders;(iv)the θ1=0.3π,θ2=0.3π,c=0.002 case from the 150ω1to the 200ω1orders,from the 200ω1to the 250ω1orders,six elliptically polarized attosecond X-ray pulses with durations and ellipticities of 23as(ε=0.1),25as(ε=0.3),21as(ε =0.3),25as(ε=0.3),18as(ε=0.3),18as(ε=0.3)can be obtained,as shown in Figs.15(a)–15(d). In conclusion,we theoretically investigate the molecular harmonic characteristic and the elliptically polarized attosecond pulse generation from H+2driven by the linearly polarized pulses.(i)Below-threshold harmonics show a resonance enhanced peak around the H7 order,which produces a red-shift(even disappearance)as the internuclear distance increased.Further analyses show this red-shift enhanced peak is caused by the laser-induced electron transfer between the ground state and the 1st excited state of H+2.(ii)Above-threshold harmonics exhibit many maxima and minima caused by the two-centre interference.Moreover,a series of anomalous elliptically polarized harmonics can be obtained with the introduction of the polarized angle.(iii)With the introduction of the spatial inhomogeneous e ff ect,not only the harmonic cuto ff s are extended,but also the harmonic modulations are reduced.Most importantly,the ellipticities of the harmonics become stable.As a result,four supercontinua with the bandwidths of 407 eV,310 eV,389 eV,and 581 eV can be obtained.Finally,by Fourier transforming the harmonics,a series of sub-25as elliptically polarized attosecond X-ray pulses with ellipticities of ε=0.1 and ε=0.3 can be obtained. Acknowledgments The authors thank Prof.Keli Han and Dr.Ruifeng Lu for providing the computational code used in the present work. References [1]T.Brabec and F.Krausz,Rev.Mod.Phys.72(2000)545. [2]F.Krausz and M.Ivanov,Rev.Mod.Phys.81(2009)163. [3]E.Goulielmakis,M.Schultze,M.Hofstetter,etal.,Science 320(2008)1614. [4]G.Sansone,F.Kelkensberg,J.F.P´erez-Torres,etal.,Nature(London)465(2010)763. [5]X.X.Zhou,X.M.Tong,Z.X.Zhao,and C.D.Lin,Phys.Rev.A 71(2005)061801. [6]L.Q.Feng and W.L.Li,Commun.Theor.Phys.63(2015)86. [7]L.Q.Feng,Phys.Rev.A 92(2015)053832. [8]Y.H.Wang,H.P.Wu,Y.Chen,etal.,AIP Advances 2(2012)022102. [9]P.B.Corkum,Phys.Rev.Lett.71(1993)1994. [10]F.Ferrari,F.Calegari,M.Lucchini,etal.,Nat.Photonics 4(2010)875. [11]I.J.Sola,E.M´evel,L.Elouga,etal.,Nat.Phys.2(2006)319. [12]F.Calegari,G.Sansone,S.Stagira,etal.,J.Phys.B:At.Mol.Opt.Phys.49(2016)062001. [13]G.Sansone,E.Benedetti,F.Calegari,etal.,Science 314(2006)443. [14]P.B.Corkum,N.H.Burnett,and M.Y.Ivanov,Opt.Lett.19(1994)1870. [15]Z.Chang,Phys.Rev.A 71(2005)023813. [16]H.C.Du and B.T.Hu,Opt.Express 18(2010)25958. [17]Q.B.Zhang,P.X.Lu,W.Y.Hong,Q.Liao,and S.Y.Wang,Phys.Rev.A 80(2009)033405. [18]C.M.Zhang,G.Vampa,D.M.Villeneuve,and P.B.Corkum,J.Phys.B:At.Mol.Opt.Phys.48(2015)061001. [19]T.J.Hammond,G.G.Brown,K.T.Kim,D.M.Villeneuve,and P.B.Corkum,Nat.Photonics 10(2016)171. [20]M.Louiy,C.L.Arnold,M.Miranda,etal.,Optica 2(2015)563. [21]C.M.Heyl,H.Coudert-Alteirac,M.Miranda,etal.,Optica 3(2016)75. [22]Z.N.Zeng,Y.Cheng,X.H.Song,R.X.Li,and Z.Z.Xu,Phys.Rev.Lett.98(2007)203901. [23]R.F.Lu,H.X.He,Y.H.Guo,and K.L.Han,J.Phys.B:At.Mol.Opt.Phys.42(2009)225601. [24]L.Q.Feng and H.Liu,Opt.Laser Technol.81(2016)7. [25]P.C.Li,C.Laughlin,and S.I.Chu,Phys.Rev.A 89(2014)023431. [26]T.Popmintchev,M.C.Chen,O.Cohen,M.Grisham,J.Rocca,M.Murnane,and H.Kapteyn,Opt.Lett.33(2008)2128. [27]L.Q.Feng and H.Liu,Laser Phys.25(2015)105301. [28]G.Orlando,P.P.Corso,E.Fiordilino,and F.Persico,J.Mod.Opt.56(2009)1761. [29]L.Q.Feng and H.Liu,Laser Phys.25(2015)015302. [30]L.Q.Feng and H.Liu,Opt.Commun.348(2015)1. [31]L.Q.Feng and T.S.Chu,Phys.Rev.A 84(2011)053853. [32]P.C.Li,X.X.Zhou,G.L.Wang,and Z.X.Zhao,Phys.Rev.A 80(2009)053825. [33]J.J.Xu,B.Zeng,and Y.L.Yu,Phys.Rev.A 82(2010)053822. [34]S.Kim,J.Jin,Y.J.Kim,I.Y.Park,Y.Kim,and S.W.Kim,Nature(London)453(2008)757. [35]L.Q.Feng and H.Liu,Phys.Plasmas 22(2015)013107. [36]M.F.Ciappina,S.S.Acimovic,T.Shaaran,etal.,Opt.Express 20(2012)26261. [37]M.F.Ciappina,J.A.P´erez-Hern´andez,T.Shaaran,L.Roso,and M.Lewenstein,Phys.Rev.A 87(2013)063833. [38]T.Shaaran,M.F.Ciappina,R.Guichard,etal.,Phys.Rev.A 87(2013)041402. [39]T.Shaaran,M.F.Ciappina,and M.Lewenstein,Phys.Rev.A 86(2012)023408. [40]X.Y.Miao and C.P.Zhao,Laser Phys.Lett.11(2014)115301. [41]X.B.Bian and A.D.Bandrauk,Phys.Rev.Lett.105(2010)093903. [42]K.J.Yuan and A.D.Bandrauk,J.Phys.B:At.Mol.Opt.Phys.45(2012)074001. [43]K.J.Yuan and A.D.Bandrauk,Phys.Rev.A 84(2011)023410. [44]K.J.Yuan and A.D.Bandrauk,Phys.Rev.A 83(2011)063422. [45]K.J.Yuan,H.Z.Lu,and A.D.Bandrauk,Phys.Rev.A 83(2011)043418. [46]K.J.Yuan and A.D.Bandrauk,Phys.Rev.A 81(2010)063412. [47]K.J.Yuan and A.D.Bandrauk,Phys.Rev.Lett.110(2013)023003. [48]D.B.Miloˇsevi´c,W.Becker,and R.Kopold,Phys.Rev.A 61(2000)063403. [49]H.C.Du,Y.Z.Wen,X.S.Wang,and B.T.Hu,Chin.Phys.B 23(2014)033202. [50]J.Levesque,Y.Mairesse,N.Dudovich,H.P´epin,etal.,Phys.Rev.Lett.99(2007)243001. [51]X.Zhou,R.Lock,N.Wagner,W.Li,H.C.Kapteyn,and M.M.Murnane,Phys.Rev.Lett.102(2009)073902. [52]O.Smirnova,S.Patchkovskii,Y.Mairesse,etal.,Phys.Rev.Lett.102(2009)063601. [53]A.Etches,C.B.Madsen,and L.B.Madsen,Phys.Rev.A 81(2010)013409. [54]I.Yavuz,Y.Tikman,and Z.Altun,Phys.Rev.A 92(2015)023413. [55]L.Q.Feng,M.H.Yuan,and T.S.Chu,Phys.Plasmas 20(2013)122307. [56]R.F.Lu,P.Y.Zhang,and K.L.Han,Phys.Rev.E 77(2008)066701. [57]X.Cao,S.C.Jiang,C.Yu,etal.,Opt.Express 22(2014)26153. [58]C.Yu,H.X.He,Y.H.Wang,Q.Shi,Y.D.Zhang,and R.F.Lu,J.Phys.B:At.Mol.Opt.Phys.47(2014)055601. [59]J.Hu,K.L.Han,and G.Z.He,Phys.Rev.Lett.95(2005)123001. [60]K.Burnett,V.C.Reed,J.Cooper,and P.L.Knight,Phys.Rev.A 45(1992)3347. [61]S.K.Son,D.Telnov,and S.I.Chu,Phys.Rev.A 82(2010)043829. [62]P.Antoine,B.Piraux,and A.Maquet,Phys.Rev.A 51(1995)R1750. [63]X.B.Bian and A.D.Bandrauk,Phys.Rev.A 83(2011)041403. [64]L.Q.Feng and H.Liu,J.Mol.Model 21(2015)43. [65]L.Q.Feng and T.S.Chu,Commun.Comput.Chem.1(2013)52. [66]M.Lein,Phys.Rev.Lett.94(2005)053004. [67]D.A.Telnov and S.I.Chu,Phys.Rev.A 80(2009)043412.[68]D.A.Telnov and S.I.Chu,Phys.Rev.A 76(2007)043412.[69]M.Lein,N.Hay,R.Velotta,etal.,Phys.Rev.A 66(2002)023805. [70]K.N.Avanaki,D.A.Telnov,and S.I.Chu,Phys.Rev.A 90(2014)033425. [71]Y.Mairesse,A.D.Bohan,L.J.Frasinski,etal.,Science 302(2003)1540.






4 Conclusion
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Exact Calculation of Antiferromagnetic Ising Model on an Inhomogeneous Surface Recursive Lattice to Investigate Thermodynamics and Glass Transition on Surface/Thin Film∗
- Higher-Order Corrections to Earth’s Ionosphere Shocks∗
- Ground State Properties of Z=126 Isotopes within the Relativistic Mean Field Model∗
- Electron-Positron Pair Production in Strong Fields Characterized by Conversion Energy∗
- Relativistic Bound and Scattering Amplitude of Spinless Particles in Modi fi ed Schioberg Plus Manning–Rosen Potentials
- An Improved Singularity Free Self-Similar Model of Proton Structure Function
