Higher-Order Corrections to Earth’s Ionosphere Shocks∗

H.G.Abdelwahedand E.K.El-ShewyPlasma Technology and Material Science Unit(PTMSU),Physics Department,College of Science and Humanitarian Studies,Prince Sattam bin Abdulaziz University,Alkharj,KSA

2Theoretical Physics Group,Physics Department,Faculty of Science,Mansoura University,Mansoura,Egypt

1 Introduction

Research on ion-acoustic waves(IAWs)in ion pair plasmas has gained considerable amount of momentum over the last few years.[1−2]Positive-negative ion have been observed in many astrophysical environments.[3]More speci fically,Negative ions are present in D-region altitudes of the ionosphere of Earth in coexistence with electrons as they are formed primarily by electron added to electronegative species.[4]In last few years,ion solitary waves in ion-pair plasmas investigated both numerically and experimentally.[5−6]In past,the nonthermal particles observed in many space environments.[7−9]However,several theoretical studies on nonlinear waves show that,electrons and ions non-thermal distributions are convenient in analyzing observation data in space plasma.[7−12]Cairns etal.[9]discussed the nonthermal electron e ff ect on the ion acoustic wave existence.Elwakil etal.[2]inspected ion acoustic modulation instability characteristics in plasma having nonthermal electronsand positive-negative ions.It is reported that,the instability conditions a ff ected by nonthermal electron parameter in D and F regions in Earth’s ionosphere.Gill etal.[13]investigated rarefactive and compressive soliton properties in two polarized ions plasma.Recently,nonthermality e ff ect of positron-electron have been examined on the properties of improved compressiverarefactive solitons generated in warm ion plasma.[14]On the other hand,there are many theoretical methods for studying nonlinear properties in plasma physics.Reductive perturbation analysis(RPT)aim to study the propagation of small wave amplitude.[15]As the wave amplitude enlarge,the solitary pro fi le sidetrack from the nonlinear equation.In order to beat this deviation,the amplitude modulation of electrostatic nonlinear waves has been studied by many investigators.[16−19]Kalejahi etal.[19]discussed the higher order nonlinear e ff ects in a relativistic plasma.Abdelwahed and El-Shewy[16]improved the soliton shape of solitary wave directly by using algebraic analysis for solving the field equations.Chatterjee etal.[17]examined the region of solitary wave existence in nonthermal ions plasma.They discussed the e ff ect of nonthermal ions and electron density on the properties of obtained dressed form.Accordingly,to improve the description of experimental data,the e ff ect of fl uctuation of charge of dusty plasma on the dressed nonlinear soliton waves has been investigated.[20]On the other hand,dusty size e ff ect on the dressed soliton like wave amplitude and energy have been discussed in dust plasma containing dust grains and nonthermal ions.[21]Physically,some phenomenon like kinematic viscosity,collisions between plasma components and Landau damping are responsible for shocks formation in Earth ionosphere.[22−24]The shock wave existence and propagation have been investigated experimentally and theoretically.[25−31]Cairns etal.[32]investigated laminar ion shocks to explain observations on ion acceleration laser plasmas.Abdelwahed[33]obtained the higher order dissipation in terms of Burger-type equation to modulate the broadband auroral electrostatic shock noise.From theoretical point of view,Kadomtsev–Petviashvili–Burgers(KPB)equation has been derived by Hussain etal.[34]They discussed the di ff raction and dissipation e ff ects on the shock wave structures in epi plasma with kappa distributed positrons and electrons.More speci fically,the obliqueness of solitary shocks in a magnetized viscous plasma have been studied.[35]Abdelwahed and el-Shewy[36]studied the nonlinear features of rational and double layer ion acoustic solitary solutions.Furthermore,Masood and Rizvi[37]investigated the viscosity e ff ect of negative and positive ions in dissipative plasma medium in a planar geometry.Also,kinematic viscosity e ff ect on formation of shock waves in asymmetric pair ion plasmas has been examined.[38]It was noted that,kinematic viscosity enhances the amplitude of shock pro fi le.In this study,the higher-order acoustic shock modulation in plasmas with negative-positive ions and nonthermal electrons have been considered.In Sec.2,the equations of the system is presented,and higher-order Burgers equation is derived in Sec.3.In Sec.4,the solutions of the higherorder Burgers-equation are presented.Finally,the results and discussion are recapitulated in Sec.5.

2 Basic Equations

A system of three collisionless unmagnetized plasmas components having viscous fl uid of positive(+)and negative(−)ion and nonthermally electron distribution.The normalized equations are given by:

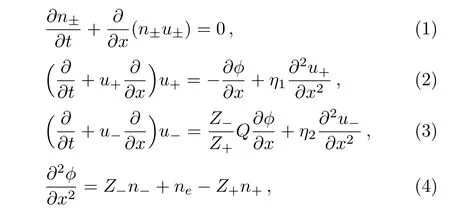
neis the electrons density obey nonthermally distributed.[9]

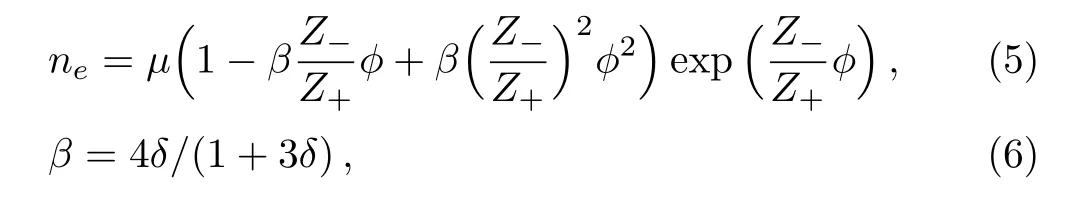
where δ is the electron nonthermality parameter andµ=ne0/n+0is the unperturbed electron to positive ion ratio.In Eqs.(1)–(5),n+(n−)is positive(negative)ionic density(normalized by n+0(n−0),u+(u−)is positive(negative)ion fl uid velocity normalized by the ion sound speed

and ϕ is electrostatic wave potential(normalized by KBTe/eZ+).x(t)is space(time)coordinate,x is normalized to Debye length of hot electron

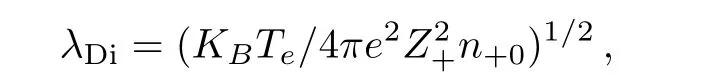
t normalized by inverse of plasma frequency of cold electron

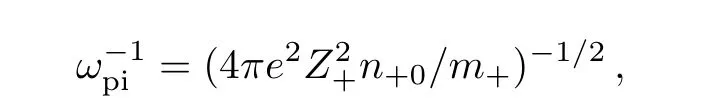
where KBis the Boltzmann constant.Teis the electron temperature,ν =n−0/n+0,and the Q(mass ratio)=m+/m−,where m+and m−are positive and negative ion masses,respectively.Also,Z±is ionic charge number.The positive(negative)kinematic viscosity η+(η−)are normalized by η+=and η−=The neutrality condition implies:

for simplicity we shall consider(Z+=Z−=1).

2.1 Nonlinear Calculations

The slow stretched co-ordinates in(RPT)method[15]are given by:

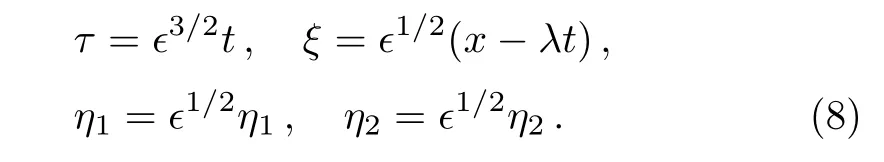
The speed of the wave λ and ϵ is a small real parameter.Expanding quantities in Eqs.(1)–(5)about their equilibrium values:

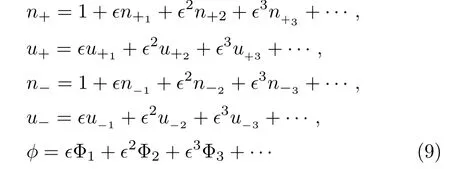
The last equations are valid with conditions:|ξ|→ ∞,n−=n+=1,u+=0,ϕ =0.Using Eqs.(8)and(9)into Eqs.(1)–(6)for quasi-neutrality condition at equilibrium,[39]the lowest-order in ϵ gives:

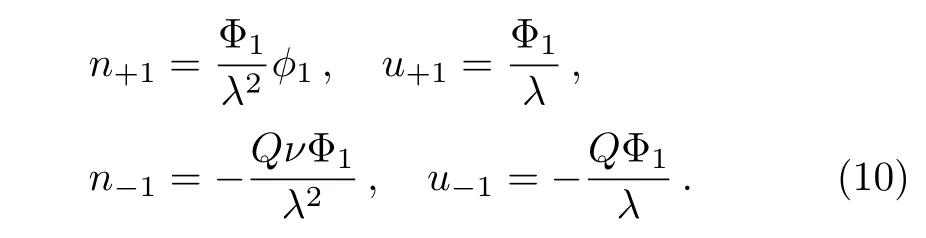
The dispersion form is given by:

The next equations of O(ϵ2)yield:

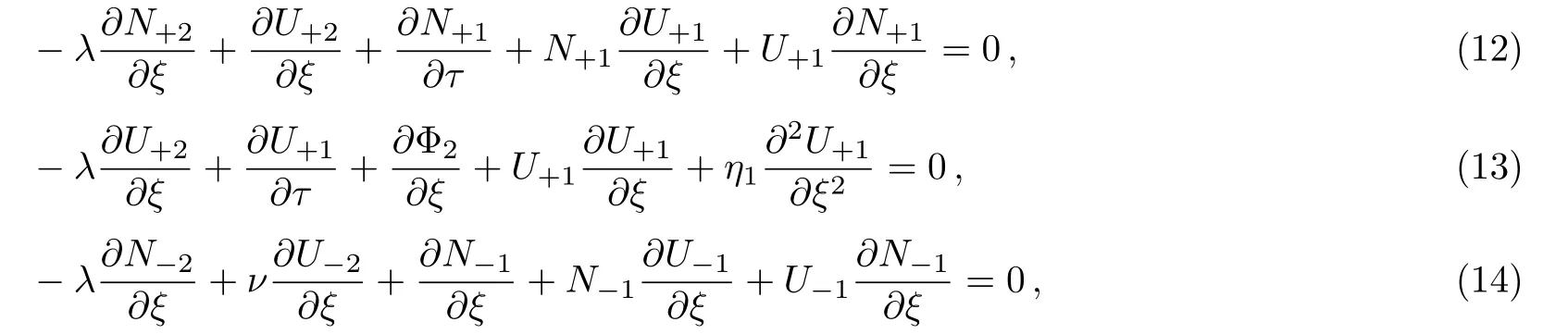
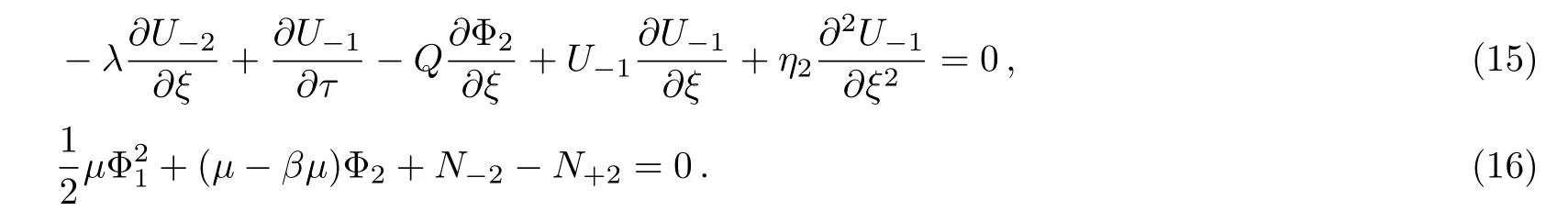
Put outN+2,N−2,ϕ2,U+2,and U−2in Eqs.(12)–(16),one obtained the Burger equation for ϕ1:

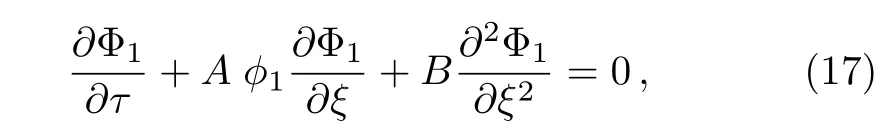
where

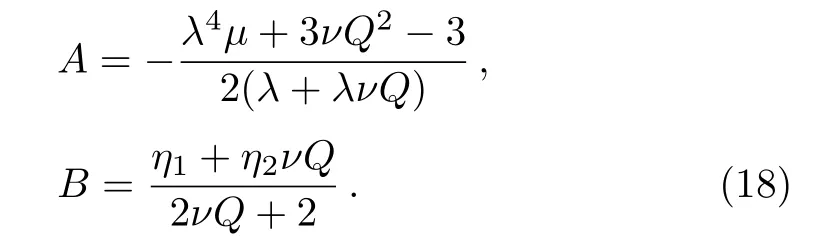
Equation(17)admits the IA shock wave solution as

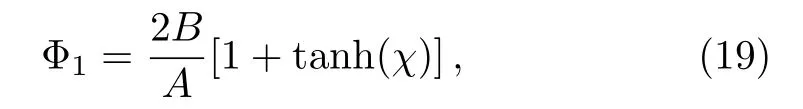
whose amplitude equals 2B/A with χ(= ξ−2Bτ).

The physical quantitiesN+2,N−2,U+2and U−2can be rewritten as:

Equations for the next order in ϵ are given by:

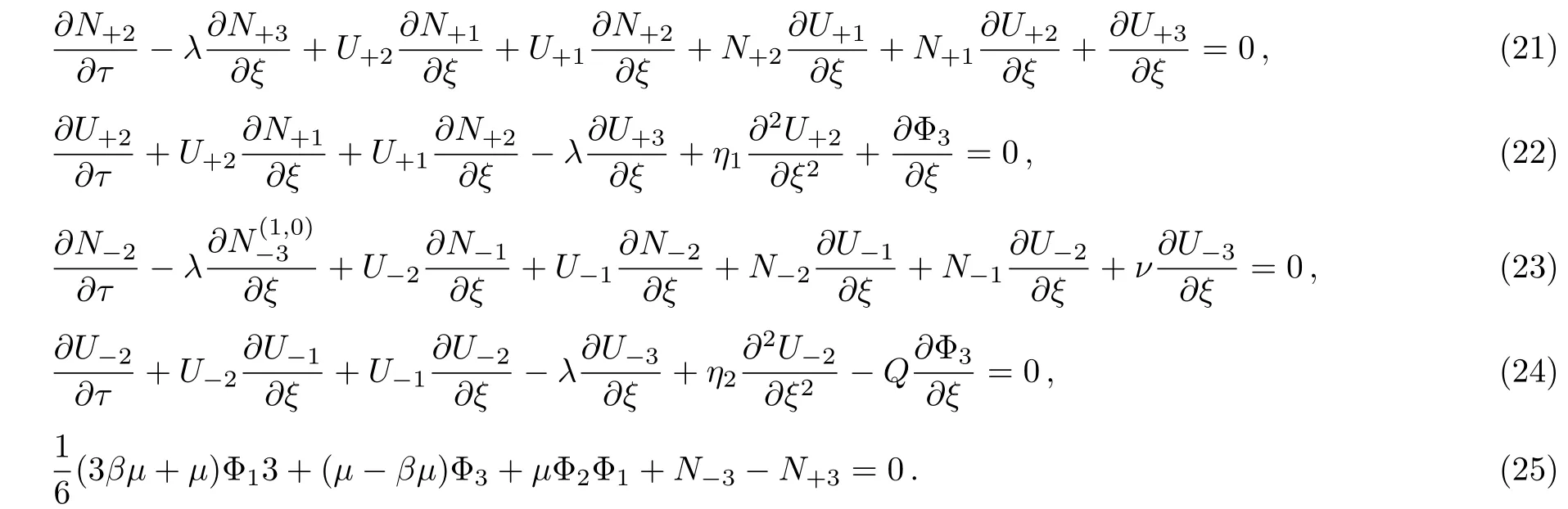
EliminatingN+2,N−2,U+2,U−2and ϕ3from Eqs.(21)–(25),we get a linearly inhomogeneous Burger type equation for ϕ1and ϕ2:

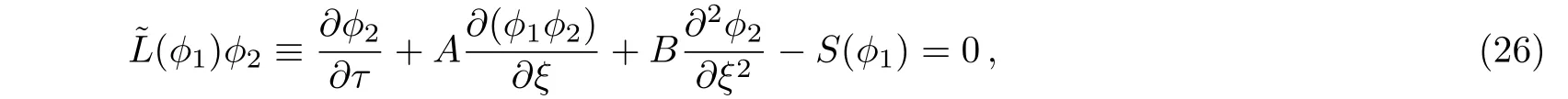
where

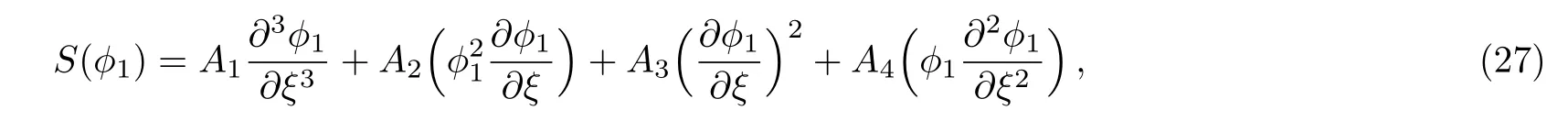
where the coefficients Ai(where i=1,2,...,4)are given by:

In summary,our model reduced to nonlinear Burger equation(17)for ϕ1and Burger type equation(26)for ϕ2;source term(28)is a function ϕ1.

3 Stationary Solution

By using Eq.(19),Eq.(27)can be transformed into the form:

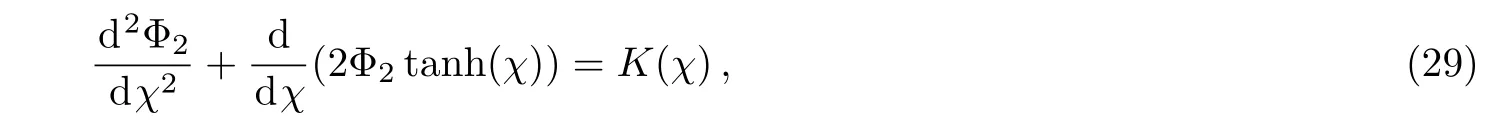
where

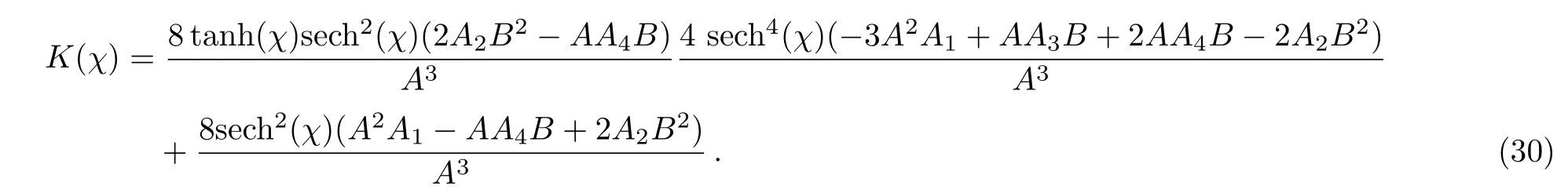
According to the homogeneous equation of Eq.(29)has two independent solutions,one of them is,(V)=sech2(χ),and the other,which can be derived using reduction of order method along with Able’s theorem,is given by(χ)=[χ/2+(1/4)sech(2χ)]sech2(χ).Using the variation of parameters method,[40−41]the particular solution of Eq.(29)can be written as

where L1(ψ)and L2(ψ)are given by

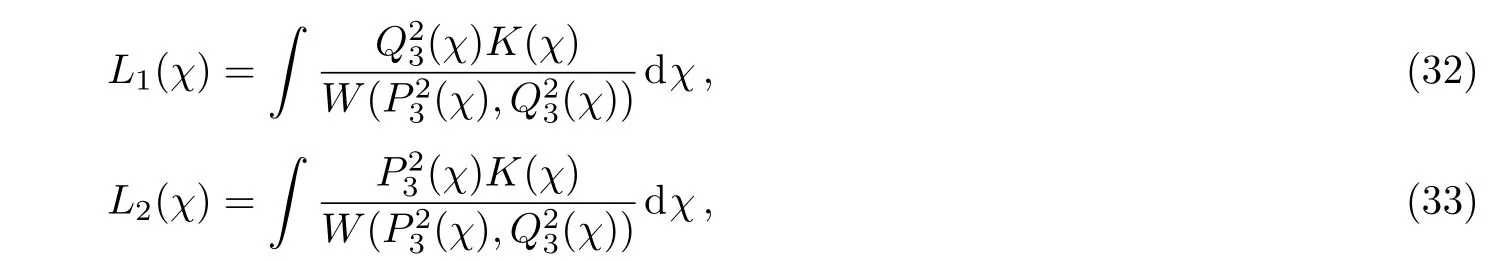
with

Then,the formal stationary IA shock solution is given by:

4 Model Results and Discussions

Shock waves are studied in unmagnetized viscous positive negative ion plasmas.Numerical values have been introduced for Earth’s ionosphere(D-and F-regions).[1−2,22−23]According to the wave dissipation caused by kinematic viscosity,the studied system supports electrostatic shock waves.However,the main essential stimulus was to study the contribution of higher-order electric field structures associated to the shock waves.The comparison of lowest order and higher-order shock noise and associated electric field structures are shown in Fig.1.It is shown that higher-order decreases both steepness and amplitude of shock form and modulates the associated electric field structure.We have studied the e ff ectuation of plasma parameters such as the population of nonthermal electrons δ,the kinematic viscosities coefficient of positive negative ions η1and η2and the ion mass ratio Q(=m+/m−)on the dynamics formation of higher-order broadband electrostatic shock noise.For example,Fig.2 shows that,the increase of electron nonthermal parameter δ decreases shock steepness and amplitude.Accordingly,the amplitude and width of associated electric field of shock structure decreased also.On the other hand,the e ff ect of kinematic viscosity coefficients of positivenegative ions η1and η2on higher-order shock pro fi le ϕ and associated electric field structuresEfhave been examined in Figs.3–4.It is found that as η1and η2increase the steepness,amplitude of higher-order shock wave and higher-order electric field structures associated to the shock waves.The physical reason for this behavior is that the increase of kinematic viscosity coefficients increases the dissipation and consequently causes strong shock wave and associated electric field structures.Finally,the ratio raise of positive-negative mass Q decreases both wave amplitude and steepness of electrostatic shocks as shown in Fig.5.In summary,it has been noted that the involvement of higher-order e ff ects,positive-negative mass ratio Q,electron nonthermal parameter δ and kinematic viscosities coefficient of positive and negative ions η1and η2would regulate the countenance of ion electrostatic acoustic shock waves in D-and F-regions of Earth’s ionosphere.

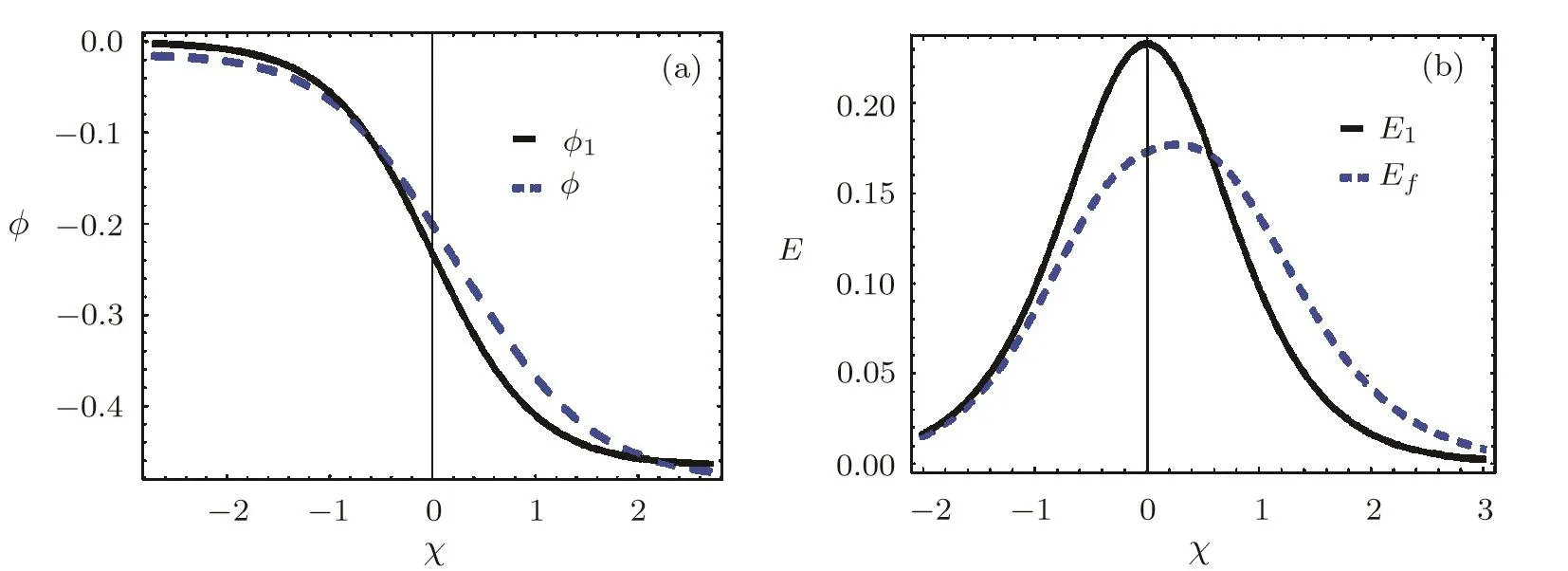
Fig.1 The comparison of lowest and higher-order shock pro fi le and associated electric field structures for Q=0.03,η1=0.3,η2=0.2,ν =0.5,and δ=0.2.

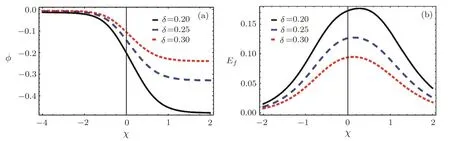
Fig.2 Variation of higher-order shock pro fi le ϕ and associated electric field structures Efvs. χ and δ for Q=0.03,η1=0.3,η2=0.2,ν =0.5.

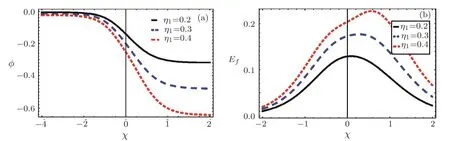
Fig.3 Variation of higher-order shock pro fi le ϕ and associated electric field structures Efvs. χ and η1for Q=0.03,η2=0.2,ν =0.5,and δ=0.2.

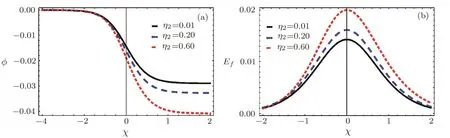
Fig.4 Variation of higher-order shock pro fi le ϕ and associated electric field structures Efvs. χ and η2for Q=0.03,η1=0.03,ν =0.5,and δ=0.2.

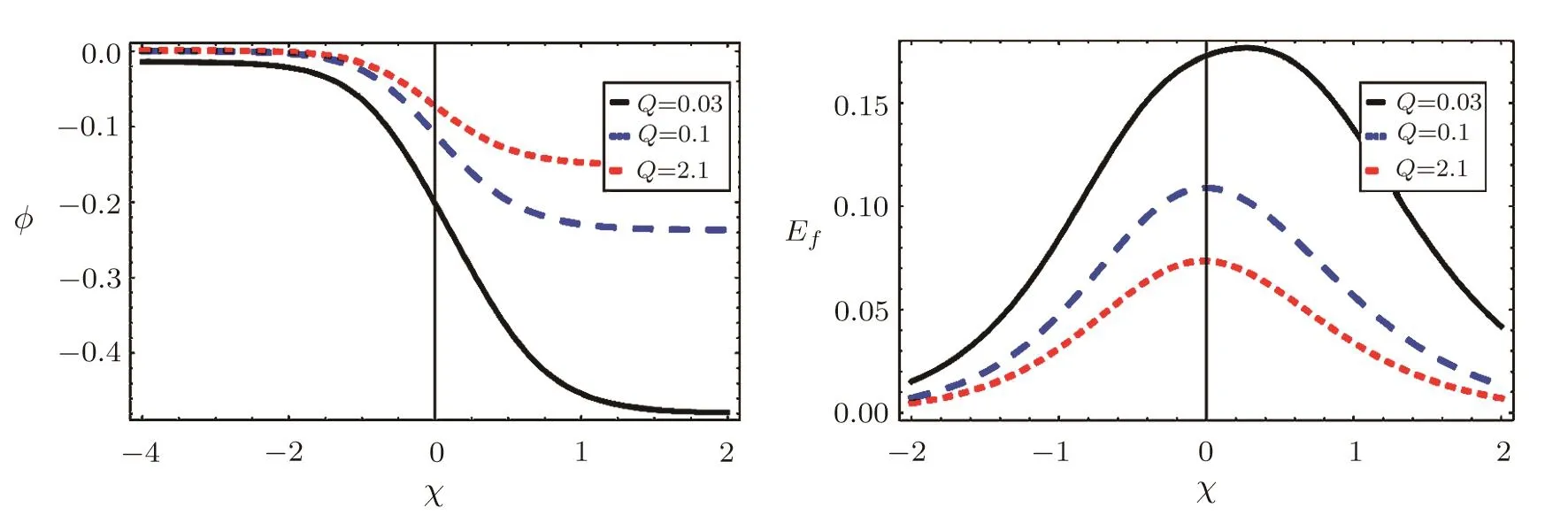
Fig.5 Variation of higher-order shock pro fi le ϕ and associated electric field structures Efvs. χ and Q for η1=0.3,η2=0.2,ν =0.5,and δ=0.2.

5 Conclusion

Ion shock waves are discussed in three collisionless unmagnetized plasmas components having viscous fl uid of positive(+)and negative(−)ion and nonthermally electron distribution.The nonlinear Burger equation(17)for lowest order and linear inhomogeneous Burger type equation(26)for higher-order dissipation are obtained.Renormalization technique gives stationary solution for perturbation theory equations.It is emphasized that steepness and amplitude of higher-order shock waves are sensitive to higher-order e ff ects,positive-negative mass ratio Q,electron nonthermal parameter δ and kinematic viscosities coefficient of positive(negative)ions η1(η2).It is clear to con fi rm that the increase(decrease)of η1and η2(Q and δ)can lead to the increase of higher-order broadband electrostatic shock amplitude.The results obtained may be useful in understanding electrostatic shock noise in Earth’s ionosphere.

References

[1]R.Sabry,W.M.Moslem,and P.K.Shukla,Phys.Plasmas 16(2009)032302.

[2]S.A.Elwakil,E.K.El-Shewy,and H.G.Abdelwahed,Phys.Plasmas.17(2010)052301.

[3]H.Massey,Negative Ions,3rd ed.Cambridge University Press,Cambridge(1976).

[4]A.J.Coates,F.J.Crary,G.R.Lewis,D.T.Young,J.H.Waite,and E.C.Sittler,Geophys.Res.Lett.34(2007)L22103.

[5]H.Saleem,Phys.Plasmas 14(2007)014505.

[6]W.Oohara,Y.Kuwabara,and R.Hatakeyama,Phys.Rev.E 75(2007)056403;W.Oohara and R.Hatakeyama,Phys.Plasmas 14(2007)055704.

[7]R.Lundin,etal.,Nature(London)341(1989)609.

[8]J.R.Asbridge,S.J.Bame,and I.B.Strong,J.Geophys.Res.73(1968)5777.

[9]R.A.Cairns,A.A.Mamun,R.Bingham,R.Bostr¨om,R.O.Dendy,C.M.C.Nairns,and P.K.Shukla,Geophys.Res.Lett.22(1995)2709.

[10]B.Sahu and R.J.Roychoudhury,Phys.Plasmas 13(2006)072302.

[11]M.M.Masud,M.Asaduzzaman,and A.A.Mamun,Astrophysics and Space Science 343(2013)647.

[12]S.A.Elwakil,A.M.El-hanbaly,A.Elgarayhi,E.K.El-Shewy,and A.I.Kassem,Advances in Space Research 54(2014)1786.

[13]T.S.Gill,N.S.Saini,and K.Harvinder,Chaos,Solitons&Fractals 28(2006)1106.

[14]H.G.Abdelwahed,E.K.El-Shewy,M.A.Zahran,and S.A.Elwakil,Phys.Plasmas 23(2016)022306.

[15]H.Washimi and T.Taniuti,Phys.Rev.Lett.17(1966)996.

[16]H.G.Abdelwahed and E.K.El-Shewy,Phys.Plasmas 19(2012)072301.

[17]P.Chatterjee,G.Mondal,K.Roy,S.V.Muniandy,S.L.Yap,and C.S.Wong,Phys.Plasmas 16(2009)072102.

[18]P.Chatterjee,K.Roy,S.V.Muniandy,and C.S.Wong,Phys.Plasmas 16(2009)112106.

[19]A.E.Kalejahi,I.Kourakis,and P.K.Shukla,Phys.Plasmas 15(2008)(2008).

[20]H.Asgari,S.V.Muniandy,and C.S.Wong,Phys.Plasmas 17(2010)063704.

[21]E.K El-Shewy,M.A.Zahran,K.Schoepf,and S.A.Elwakil,Phys.Scr.78(2008)025501.

[22]R.Blandford and D.Eichler,Phys.Rep.154(1987)1.

[23]N.A.Strokin,Sov.Phys.J.Energy Theor.Phys.61(1985)6.

[24]S.Hussain and N.Akhtar,Phys.Plasmas 20(2013)012305.

[25]Y.Nakamura,H.Bailung,and P.K.Shukla,Phys.Rev.Lett.83(1999)1602.

[26]P.K.Shukla and S.G.Tagare,Phys.Lett.A 59(1976)38.

[27]A.Sarma and Y.Nakamura,Phys.Lett.A 373(2009)4174.

[28]E.K.El-Shewy,H.G.Abdelwahed,and M.A.Elmessary,Phys.Plasmas 18(2011)113702.

[29]A.M.El-Hanbaly,E.K.El-Shewy,A.Elgarayhi,and A.I.Kassem,Commun.Theor.Phys.64(2015)529.

[30]E.K.El-Shewy,S.A.El-Wakil,A.M.El-Hanbaly,M.Sallah,and H.F.Darweesh,Astrophys.Space Sci.356(2015)269.

[31]A.M.El-Hanbaly,M.Sallaha,E.K.El-Shewy,and H.F.Darweesh,J.Exp.Theor.Phys.121(2015)669.

[32]R.A.Cairns,R.Bingham,P.Norreys,and R.Trines,Phys.Plasmas 21(2014)022112.

[33]H.G.Abdelwahed,Phys.Plasmas 22(2015)092102.

[34]S.Hussain,S.Mahmood,and Ur-Rehman,Hafeez,Phys.Plasmas 20(2013)06210.

[35]M.Shahmansouri and A.A.Mamun,Phys.Plasmas 20(2013)082122.

[36]H.G.Abdelwahed and E.K.El-Shewy,Commun.Theor.Phys.60(2013)445.

[37]W.Masood and H.Rizvi,Phys.Plasmas 18(2011)042302.

[38]W.Masood and H.Rizvi,Phys.Plasmas 19(2012)012119.

[39]G.Mandal and P.Chatterjee,Verlag Z Naturforschung 0932(2010)0784.

[40]S.K.El-Labany,J.Plasma Phys.54(1995)295.

[41]Y.Kodama and T.Taniuti,J.Phys.Soc.Jpn.45(1978)298.