A Direct Algorithm Maple Package of One-Dimensional Optimal System for Group Invariant Solutions∗
2018-05-05LinZhang张琳ZhongHan韩众andYongChen陈勇
Lin Zhang(张琳)Zhong Han(韩众)and Yong Chen(陈勇)†
1Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China
2Department of Physics,Zhejiang Normal University,Jinhua 321004,China
1 Introduction
Symmetry group theory has a priority to gain much concern in finding exact solutions of differential equations.[1−5]The theory is commonly applied to construct explicit solutions for integrable and non-integrable nonlinear equations.Based on the theory,an original nonlinear system of any given subgroup can be reduced to a system with fewer independent variables.The reduction of the variables is established on group invariant solutions.Since in finite subgroups always exist,which means the impossibility of finding all the group invariant solutions[6−9]to the given system,the classi fication[10−20]of symmetry subgroup is essentially important in solving the problem.Then to find those complete but inequivalent groupinvariant solutions is expected.From now on,many systematic and effective method has formulated,and the concept of“optimal system” for group-invariant solutions is proposed to solve the problem.
People always find an optimal system of subalgebras instead of finding subgroups,which are equivalent.Ovsiannikov[21]initially uses the adjoint representation[22]of a Lie group on Lie algebra to classify group-invariant solutions and the method is developed by Olver,Winternitz,Zassenhaus,and Patera[23−24]afterwards.In particular,Olver[22]gave an ingenious method,which is more simple to calculate.For the one-dimensional optimal system,he successfully applied the method in the Korteweg-de Vries(KdV)equation and the heat equation.Later on,many new methods have appeared and the mechanization has been realized[25−31]through computer.The mechanized realization simpli fies complicated manual computation efficiently.So to many important partial differential equations,this has always been paid substantial concentration.
The objective of this paper is to give a newMaplepackage for constructing the one-dimensional optimal system,[32]which can be more precise and common used.Here we propose a new symbolic computation algorithm and develop aMaplepackage namedOne Optimal System.For a given Lie algebra,it can find different cases of classi fication and the corresponding one-dimensional optimal system automatically.Compared to existing software packages,the improvement of the new software package is that it gets more precise result,which is equal to Olver’s result.What is more,it can be more common used in many important partial differential equations.So we have made a meaningful improvement in constructing the onedimensional optimal system of finite dimensional Lie algebra.
This paper is arranged as follows.In Sec.2,we present some necessary de finitions and formulas refereed in the paper.Section 3 includes an illustration of essential algorithm details and description of some vital functions and variables.In Sec.4,we verify the validity and efficiency of the software package by applying it to some well-known partial differential equations.In Sec.5,we generalize the advantages and innovations of our work and propose future work expectation.
2 Conceptions and Formulas
2.1 Optimal System
SupposeGis a Lie group.We de fineHas an optimal system ofs-parameter subgroups,which are inequivalent to each other.It is a system of differential equations inp(p>s)independent variables based on a family of groupinvariant solutions.For any elementsg∈Gnot inHcan be transformed to the ones included inH.In general,the subgroups in the optimal system can represent the whole elements from the in finite subgroups of a given equation.Commonly,we use symmetry subalgebra to form an optimal system instead of subgroups.
2.2 Adjoint Representation
LetGbe ann-dimensional Lie algebra andvi(i=1...n)bengenerators in the vector fields ofG.The adjoint representation is de fined as

2.3 Invariant
Suppose a real functionϕ.For allv∈Gand allg∈G,it satis fies

Thenϕcan be called an invariant.For any invariant,two vectorsvandv′are equivalent under the adjoint action.As Olver[21]said,it is very important to find the invariant that decides how far we can simplify a Lie algebra.We expect to find all the invariants of the given symmetry algebraGin spite of Killing form.
2.4 Classi fication Rules
We classify all the generators by assigning different values to the invariants.The rules of classi fication are as follows:
(i)Check every invariant’s degree.If we find the degree of an invariant is even,we can make it either 1 or 0.On the other hand,if the degree is odd,we can make it 1,−1 or 0.
(ii)For every invariant,it must be assigned either 1 or−1(if degree is odd) firstly.And in each case,we must and just make only one invariant(marked as a flag invariant)either 1 or−1.Then the remaining invariants are assigned c at the same time.After that,we can make the flag invariant 0 with any other invariant assigned either 1 or−1.And the remaining invariants are assignedcat the same time.
(iii)Once an invariant is assigned 0,it cannot be assignedcany more.When all the invariants have been assigned either 1 or−1.The last case must be all the invariants are assigned 0.
2.5 Invariance Set
3 Algorithms
We developed an automated software packageOne Optimal SystemonMapleversions 16 and above.The package is initialized by the command withOne Optimal System. The software package is consisted of Lie Bracket,commutator,lie bracket,commutatortable,liebracket cal,Linear Co,e index,e0,eps,datadata,funset,ndeta,detapd,ep solve,judge s,speciale,aaasolve,get rid,get solution,beauty m,check30,exper30,check fun,trans ornot,excep vv,denoax,beautyc,andOne Optimalfunctions.The main function isOne Optimal:=proc(vs.,consts).We will illustrate the whole software flow and introduce algorithm of fundamental steps with some important functions and parameters description.
3.1 Overview of One Optimal System
Given the m-dimensional Lie algebraG.Firstly,we can get the commutator table by formula(7)for every pairs of generators:

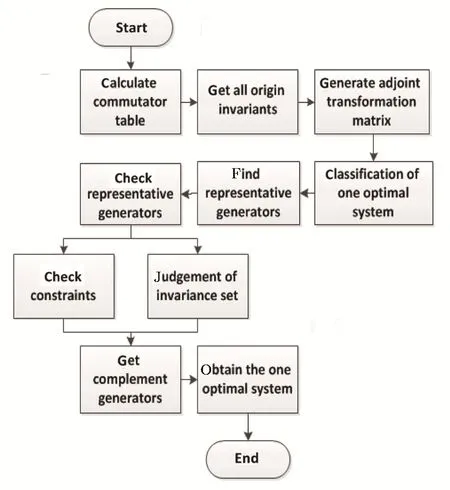
Fig.1 Software flow diagram of the One Optimal System.
By extracting the coefficients ofbi,i=1,...,n,we obtainN(N≤n)linear differential equations about
ϕ(a1,...,an).Solve the equations,the invariantϕis obtained.According to the commutator table,we can get the adjoint transformation matrix by using formula(1).Then we classi fied different cases through the classi fication rules.For each case,we must choose a representative generator and check the chosen generator in case of an incomplete representation.What is more,we should also check the existence of invariance set for more representative generators.Finally,we get all the representative generators to compose the one-dimensional optimal system.
3.2 Generation of Adjoint Transformation Matrix
We can get the adjoint representation table by using formula(2),then the adjoint transformation matrixAis obtained by calculating Eqs.(3)and(4).However,it remains a problem to do in this way.In formula(1),the degree of adjoint representation is in finite.So we will have difficulty in constructing an in finite series expansion through symbolic computation.In this situation,constructing a finite estimated series expansion is commonly to be done,but it de finitely makes the result imprecise.Here we proposed a new algorithm to solve the problem.Without calculating formula(2)directly,we extract every element of the commutator table to constructAi.TakeA1for example,it mainly depends on line 1 of the commutator table(lineiis forAi).Suppose a vectorV=[a1vm+1,...,anvm+n]in line 1 and a matrixA11.Then inA11,we can getA11[i][j]=an,wherei=n,j=m+n.After making exponential calculation ofA11,we will obtainA1.In software package,functioneindex:=proc(ct0::Matrix)realizes this process.
Here is an example for KdV equation.Table 1 is the commutator table and Eq.(11)presentsAi,i=1,...,4.
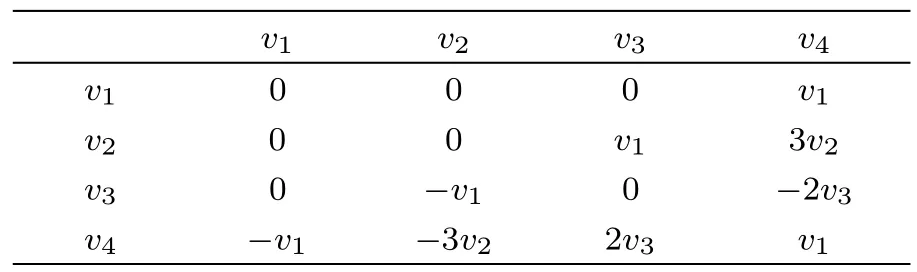
Table 1 The commutator table of KdV equation.
Compared with the old method,the new method is more sufficient and it is much easier for us to realize the calculating process through symbolic computation.Above all,the result is more accuracy than before.Functions implementing this part as well as some important parameters are in Table 2.

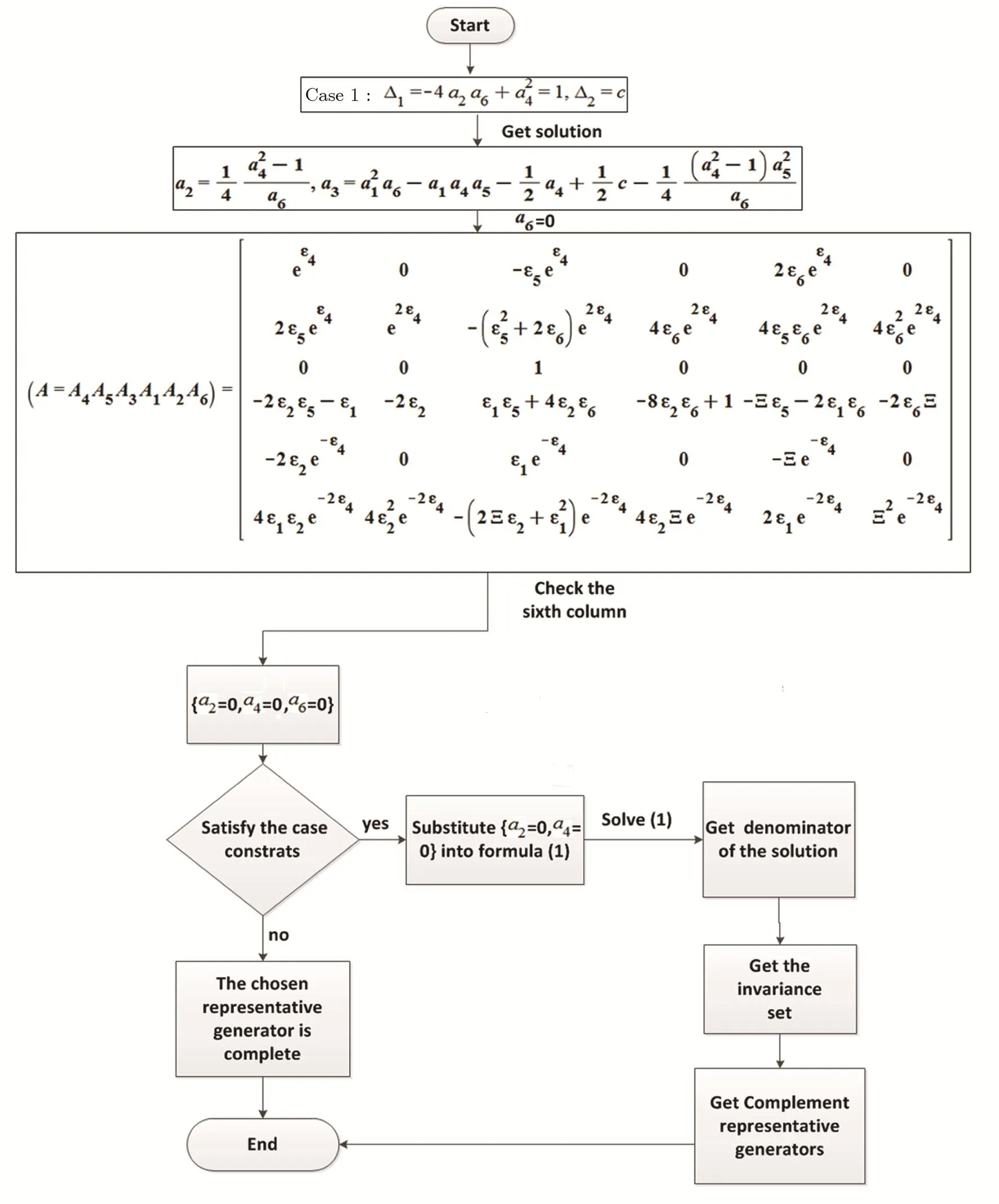
Fig.2 Software flow diagram of situation 2.

Table 2 Functions and parameters of the One Optimal System.
3.3 Classi fication of One Optimal System
After we get all the invariants,we can classify each case of one-dimensional optimal system according to classi fication rules(details in Table 3).

Table 3 Different cases of classi fication for an optimal system.
Remark
(i)We assume invariant1and invariant2are origin invariants and initialize a current invariant set to put them in.For every cases,we assign exact value to the invariants in the current invariants set according to classi fication rules.
(ii)When there is no invariant assignedc,we substitute the case constraints into the differential equation to find if new invariants(assuming invariant3and invariant4represents new invariants in each case)exists.If all the invariants in the current set are not assigned 0,we should make all new invariantsc.On the other hand,if all the invariants in the current set are assigned 0,we can add the new invariants into the current invariants set and assign exact value to them according to classi fication rules.
(iii)What we should notice is the new invariants are not constant if they are not added to the current set.The new invariants’expression depend on the differential equation,which are substituted different case constraints.
(iv)The last column of Table 3 are used to check the degree of invariants.
Functions implementing this part as well as some important parameters are described in Table 4.

Table 4 Functions and parameters of the One Optimal System.
3.4 Find the Representative Generator
(i)Find a representative generator
For each case,we must choose a representative generator and it is better to be as simple as possible.For this intention,we solve case constraint firstly.Then we assume eachaishowing in the numerator of the solution to be 0,except the one showing up in the denominator as well.And the one in the denominator should be assigned either 1 or−1,determined by another constraint(expressions likein the solution.This method can make sure of choosing more simple representative generators.
(ii)Check the representative generator
By solving Eq.(5),we can determine if the chosen representative generator is appropriate for this case.If there is a solution exists,we should also judge if there are some constraints as follows in the solution.
(a)Exists expressionslike ln(ai),
(b)Exists denominatorai.
If so,this will make the chosen representative generator not complete.That means it can not represent the whole generators of this case.Then we should find another representative generator to complement the chosen one.
Situation 1For the first situation,we give two examples in the following Table 5.

Table 5 Two examples of the first situation.
Remark
(i) If the same constraint also exists in the case constraints,we do not need to find another generator as the constraints exist originally in this case.
(ii)Solution1is for the case constraint and solution2is for Eq.(5),generator1is the origin generator and generator2is the one to make complement.
Situation 2
For this situation,it is related to the invariance set and we have a check method in Fig.2.(Remark:∆1=
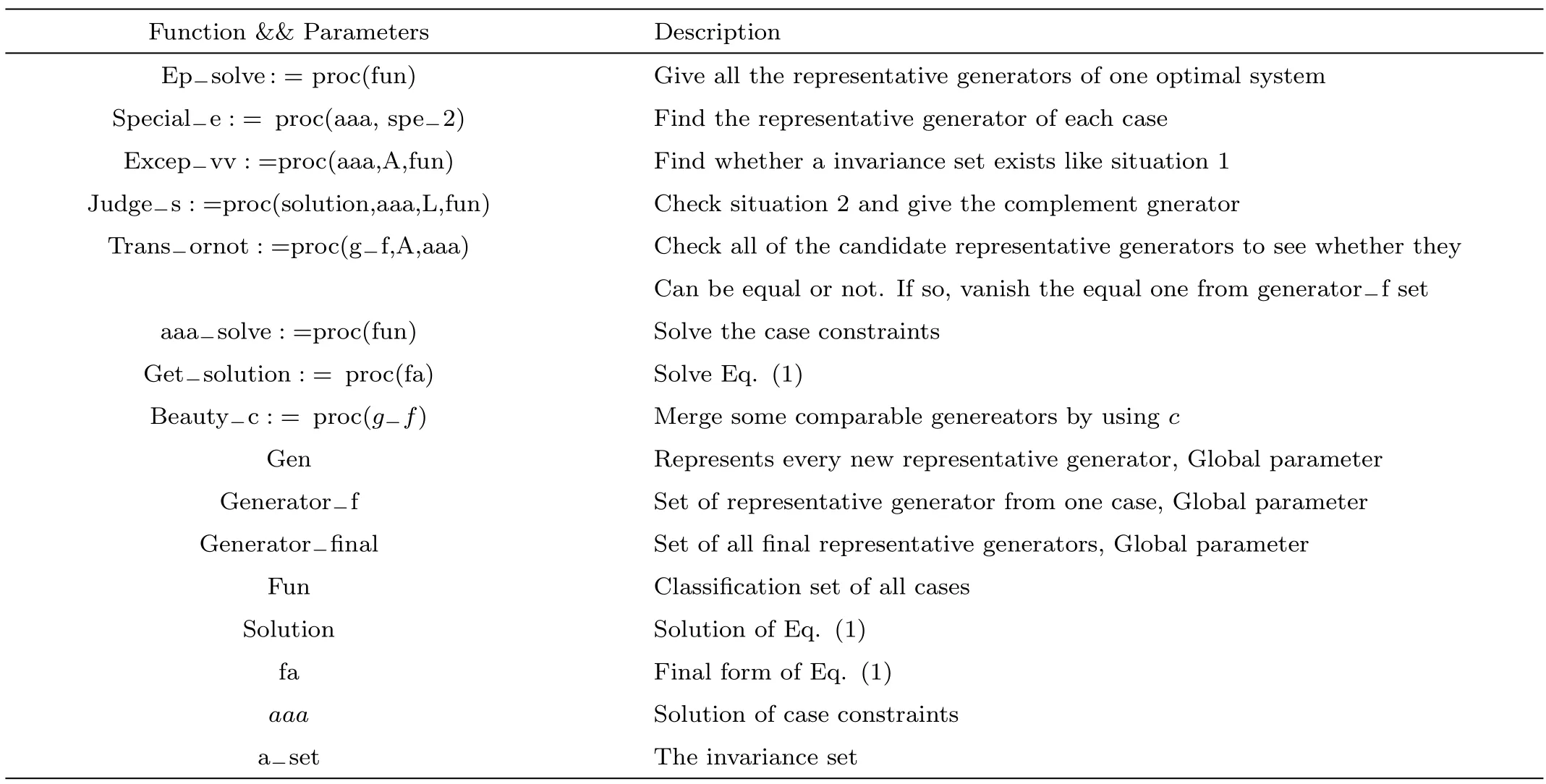
Table 6 Functions and parameters of the One Optimal System.
If we get the invariance set,we can classify two cases as follows:
(i)Make all the variants 0 in the invariance set.
(ii)Make not all the variants 0 in the invariance set.
Then we can get two new representative generators.Through the two steps above,we can find the representative generator in every cases,but there is still a special situation we should also take a consideration.Take KdV equation for example.When we find the representative generators under the case constraintswe can listv1,v2,v3as candidate representative generators corresponding to{a4=0,a2=0,a3=0},{a4=0,a3=0,a2=0},{a4=0,a2=0,a3=0}respectively.From the adjoint matrix of KdV,we can see from the adjoint transformation matrix(14)when the generator satis fies{a4=0,a2=0,a3=0},the second and third column of the matrix are 0 constantly by computing Eq.(5).So for this situation,we should check all of the candidate representative generators to see whether they are equal or not.Finally,we should list all the unequal ones to complement,
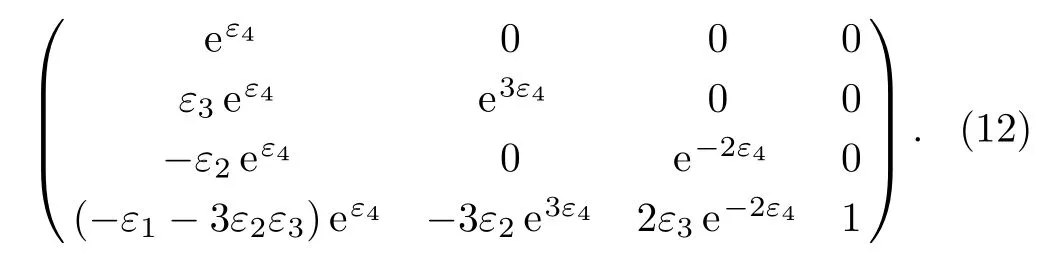
Functions implementing this part as well as some important parameters are described as in Table 6.
4 Examples
According to the previous software packageOne Optimal,[33]which generates one-dimensional optimal system of finite dimensional Lie Algebra,the result has to adjust the coefficients containingε,which is uncertainty to give a complete classi fication.This uncertainty makes problems that some of the representative generators of the one-dimensional optimal system are absent or belong to the same case.The new software packageOne Optimal Systemcan overcome this problem by giving a direct classi fication,whose answer is equal to Olver’a result.In this chapter,we apply it to many important equations to check its effectiveness and correctness.
4.1 KdV(Korteweg-de Vries)Equation


>kdv:
>One Optimal({kdv,});
—Outputs:
The commutator table is as Table 7

Table 7 The commutator table of KdV equation.
The origin invariants are:[a4].
The Optimal System is:3}.
According to Olver,[22]the one-dimensional optimal system of KdV Equation is

The result({vi|i=1,...,4}represents the same vector in Table 7 is just the same as our answer.
4.2 Heat Equation


Table 8 The commutator table of heat equation.

4.3 NS(Navier-Stokes)Equation


Table 9 The commutator table of NS equation.
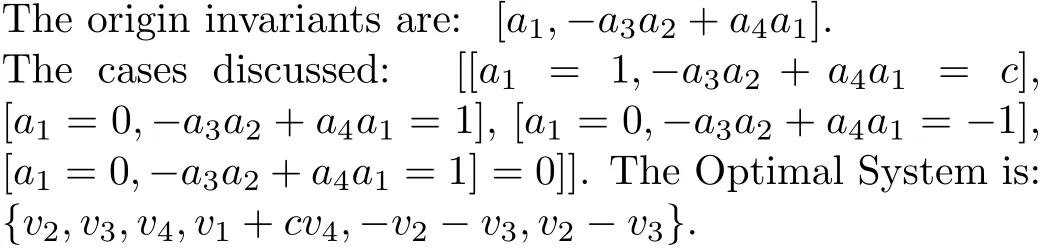
4.4 ZK(Zakharove-Kuznetsov)Equation



Table 10 The commutator table of ZK equation.

5 Conclusions
Group invariant solutions have been used to describe general solutions to PDE systems.They can be illustrated by the invariance of PDE symmetry group.We need to find group invariant solutions due to the existence of infinite different symmetry groups.To classify invariant solutions in Lie algebra,we propose a newMaplepackage calledOne Optimal System.This has a signi ficant mean-ing in the mathematics mechanization and machine learning.The mechanized realization efficiently make complicated manual computation much more simple.Especially,to many important partial differential equations,many researchers have paid substantial concentration to the theme.Compared with the previous software package,[33]this new software package is obviously more efficient than the previous one,which costs less time in operation.And we can get a perfect result that is precisely consistent with Olver’s result.And the algorithm of the new software package is more direct and programming than the previous one without many manual settings.Furthermore,the algorithm structure can be used tor-parameter(r≥2)optimal systems for further developing,which is difficult for the previous one.In this article,firstly,we use a new algorithm to calculate the adjoint transformation matrix,which effectively makes the mechanized realization much easier.Secondly,we find all the origin invariants(new ones are found in the process of classi fication)of a Lie algebra in spite of Killing form,then the classi fication rules of assigning different values to invariants regularly ensure the completeness of one optimal system.Last but not least,we check constraints of the chosen representative generator in simplest form to avoid overlooking some special situations.Simultaneously,we propose an important conception of invariance set.The software package can be applied to not only single partial differential equations,but also to ODEs and systems of differential equations.The original(1+1)-dimensional system of differential equations can be reduced to inequivalent ODEs,as a result of the one-dimensional optimal system of the symmetry Lie algebra with corresponding group invariant solutions recovered.
We realize calculation process of the one-dimensional optimal system by developingOne Optimal Systemsoftware package,which is demonstrated effective,precise and systemic.This is proved to simplify the manual computation signi ficantly and has made a contribution to mathematics mechanization.To achieve more pervasive mechanized application of this method,we will devote to developing new software package ofr-parameter(r≥2)optimal systems in the future.
We would like to express our sincere thanks to S.Y.Lou,X.R.Hu,and Q.Miao for their valuable comments and suggestions.
[1]S.Lie,Arch.Math.6(1881)328.
[2]J.Lin and H.Wang,Optics Commun.298(2013)185.
[3]A.L.Guo and J.Lin,Commun.Theor.Phys.57(2012)523.
[4]Y.K.Liu and B.Li,Chin.J.Phys.54(2016)718.
[5]W.G.Cheng,B.Li,and Y.Chen,Commun.Nonl.Sci.Numer.Simu.29(2015)198.
[6]X.R.Hu and Y.Chen,Appl.Math.Comput.215(2009)1141.
[7]Z.Z.Dong,F.Huang,and Y.Chen,Z.Naturforsch.66a(2011)75.
[8]X.R.Hu,Z.Z.Dong,F.Huang,and Y.Chen,Z.Naturforsch.65a(2010)1.
[9]Z.Z.Dong,Y.Chen,D.X.Kong,and Z.G.Wang,Chin.Ann.Math.33(2012)309.
[10]N.H.Ibragimov,CRC Handbook of Lie Group Analysis of Differential Equations,CRC Press,Boca Raton(1994).
[11]X.R.Hu,Y.Chen,and L.J.Qian,Commun.Theor.Phys.55(2011)737.
[12]Z.Z.Dong and Y.Chen,Commun.Theor.Phys.54(2010)389.
[13]F.Galas and E.W.Richter,Physica D 50(1991)297.
[14]L.Gagnon and P.Winternitz,J.Phys.A 22(1989)469.
[15]L.Gagnon,B.Grammaticos,A.Ramani,and P.Winternitz,J.Phys.A 22(1989)499.
[16]L.Gagnon,P.Winternitz,J.Phys.A 21(1988)1493.
[17]K.S.Chou,G.X.Li,and C.Z.Qu,J.Math.Anal.Appl.261(2)(2001)741.
[18]X.R.Hu and Y.Chen,Commun.Theor.Phys.52(2009)997.
[19]S.V.Coggeshall and J.Meyer-Ter-Vehn,J.Math.Phys.33(1992)3585.
[20]J.C.Fuchs,J.Math.Phys.32(1991)1703.
[21]L.V.Ovsiannikov,Group Analysis of Differential Equations,Academic,New York(1982).
[22]P.J.Olver,Applications of Lie Groups to Differential Equations,Springer,New York(1993).
[23]J.Patera,R.T.Sharp,P.Winternitz,and H.Zassenhaus,J.Math.Phys.17(1976)986.
[24]L.Weisner,Canad.J.Math.Phys.11(1959)141.
[25]A.K.Head,Program BIGLIE for Lie Analysis of Differential Equations on IBM Type PCs,Users Manual(2000).
[26]J.Carminati and K.Vu,J.Symbolic Comput.29(2000)95.
[27]A.K.Head,Program LIE for Lie Analysis of Differential Equations on IBM Type PCs,User’s Manual(2000).
[28]Baumann,Symmetry Analysis of Differential Equations with Mathematica,Springer,New York(2000).
[29]E.S.Cheb-Terrab,and K.von Bulow,Comp.Phys.Comm.90(1995)116.
[30]K.T.Vu,J.Butcher,and J.Carminati,Comp.Phys.Comm.176(2007)682.
[31]F.Schwarz,SIAM Rev.30(1988)450.
[32]X.R.Hu,Y.Q.Li,and Y.Chen,J.Math.Phys.56(2015)053504
[33]Q.Miao,X.R.Hu,and Y.Chen,Commun.Theor.Phys.61(2014)160.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Solitary Potential in a Space Plasma Containing Dynamical Heavy Ions and Bi-Kappa Distributed Electrons of Two Distinct Temperatures
- Ti Impurity Effect on the Optical Coefficients in 2D Cu2Si:A DFT Study∗
- Simultaneous Effects of Impurity and Electric Field on Entropy Behavior in Double Cone-Like Quantum Dot
- Electron Acceleration by Beating of Two Intense Cross-Focused Hollow Gaussian Laser Beams in Plasma∗
- Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow∗
- Unique Outcomes of Internal Heat Generation and Thermal Deposition on Viscous Dissipative Transport of Viscoplastic Fluid over a Riga-Plate
