Ground State Properties of Z=126 Isotopes within the Relativistic Mean Field Model∗

Qi-Xin Yu(余圻昕),Jun-Qing Li(李君清),and Hong-Fei Zhang(张鸿飞)School of Nuclear Science and Technology,Lanzhou University,Lanzhou 730000,China

2College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China

3Institute of Modern Physics,Chinese Academy of Science,Lanzhou 730000,China

4Department of Physics,Tianshui Normal University,Tianshui 741001,China

1 Introduction

Highlights from superheavy element research in the past 10 years include the synthesis of new elements up to Z=118,and there is an indication that a gradual onset of increasing stability for isotopes with Z＞111.[1]Back in the 1960s,various theoretical calculations have predicated the next doubly shell closures beyond208Pb at proton number Z=114 or 126,and at neutron numberN=184.[2−4]Up to now,superheavy elements(SHEs)with charge number Z 6 118 have been produced via coldfusion reactions with Pb or Bi as targets[5−7]or hot-fusion reactions with48Ca as projectiles.[8−9]Furthermore,there are also some attempts to synthesize superheavy nuclei(SHN)with Z＞118 to determine whether the magic proton number exist at Z=114 or at higher proton numbers Z=120–126.[10]So studying the ground state properties of Z=126 in this work shows much more importance for the understanding of nuclear structure.However,it is hard to find any consensus or semblance results among different theories with regard to the ground state properties of SHN,plenty of predictions have been made about the stability of nuclei and the possible magic numbers of proton and neutron in superheavy nuclear region.In the last few decades,the relativistic mean field theory(RMF)has been developed and applied by quantity of authors.Serot and Walecka etal.gave the detailed reviews for RMF theory,[11−12]and the great progress was maken for RMF recently.[13−16]It is noteworthy that predictions have been made about Z=126 in Refs.[17–21].Skyrme–Hartree–Fock method and a macroscopic-microscopic model have been applied for the study of SHN,and they predicted Z=114,120 or 126 as the proton magic number andN=172 or 184 as the neutron magic number.Thus,it is essential to have a fully understanding of the properties of nuclei in this region.

It is noteworthy that the“island of stability of superheavy nuclei”is rather sensitive to the models and parameters of the theories.The RMF theory has already been used to calculate the properties for SHN[19,22−23]successfully,especially in Refs.[24–27],the experimental data of SHN have been reproduced by RMF with the parameters NL-Z2 and some valuable predictions are provided.

The aim of this work is to investigate the ground state properties of Z=126 isotopic chain and check whether Z=126 is the proton magic number.The framework of RMF will be outlined in Sec.2,and the calculations of the ground state properties of Z=126,including binding energies,isotopic shifts,two-nucleon separation energies,α decay energies,pairing energies and quadrupole deformations will be discussed in Sec.3.Section 4 summarizes the main conclusions.

2 Theoretical Framework

We start the RMF theory from the Lagrangian density,whereby nucleons are described as Dirac spinors interacting by the exchange of mesons:isoscalar mesons(σ),isoscalar vector mesons(ω),isovector vector mesons(p).Because of the particular details of RMF can be found in Refs.[28–29],we will present the essential formalism and equations for fi nite nuclei,

where isovector quantities are indicated by letters with arrow bars.The field for the σ-meson is denoted by σ,that of the ω-meson by ω and of the isovectorp-meson by.M,mσ,mωandpare the nucleon,the σ-,the ωand thep-meson masses respectively,while gσ,gω,gpand e2/4π=1/137 are the coupling constants for the mesons and photon.On the other hand,the lagrangian contains a nonlinear potential proposed by Boguta and Bodmer,[30]which is essential for appropriate description of surface properties,

The field tensors for the vector mesons and the electromagnetic field take the following forms:

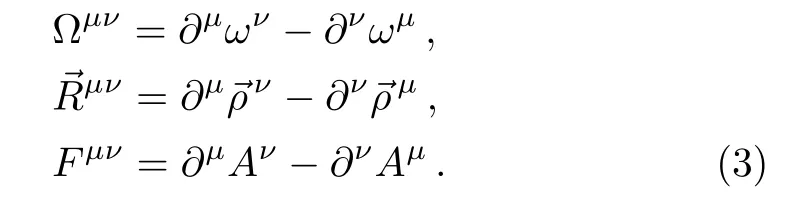
The equations of motion for these fields are derived with the classical variational method,and the Dirac equation for the nucleons and the Klein–Gordan equations can be written as[28]

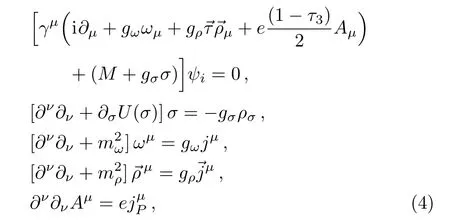
whereps(r)is the scalar density for σ- field:

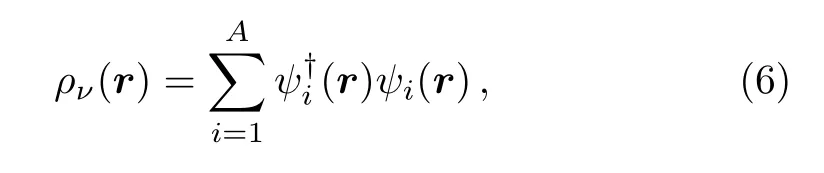
the vector densitypν,which is identical to the baryon density:p3indicates the di ff erence between the neutron and proton densities.

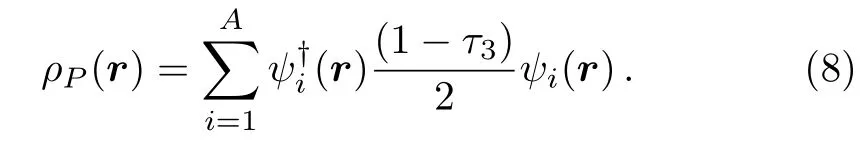
In the present calculations,the contribution of the antiparticles is neglected,i.e.the no sea approximation is proposed.The Dirac equation is taken as:

where the εiindicates the single particle energies.The e ff ective mass M∗(r)for fi nite nuclei dependent on the σ- field is given by:

Symmetries can simplify the calculations considerably.[28]Because of the time reversal and charge conservation are considered,the spacial components ω,and A vanish,the components of time-like ω0,,and A0left only.Thus,the vector potential V(r)takes the form:

2.1 一般资料 两组患者在性别比、年龄、体重等方面比较统计均无显著性差异（P＞0.05），见表1。两组患者喉罩置入与气管插管均为1次性成功。

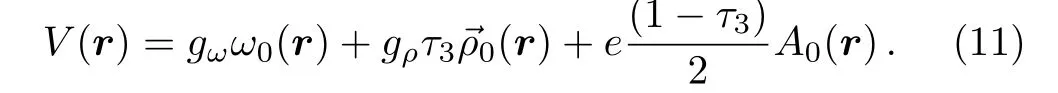
and the proton densitypPfor the photon field:

The equations of Klein–Gordan with the nucleon densities as sources in Eqs.(5)–(8)for these meson fields can be written as:

It is noteworthy that the solutions of Dirac equation and Klein–Gordan equations are obtained by expansion in the axially symmetric harmonic oscillator basis with 20 major shells for fermions and bosons respectively.[31,33]It is well known the pairing correlations are crucial for open shell nuclei,which is treated by the BCS theory in this work.The pairing strength for the neutrons and protons are taken as the following forms:[31−32]

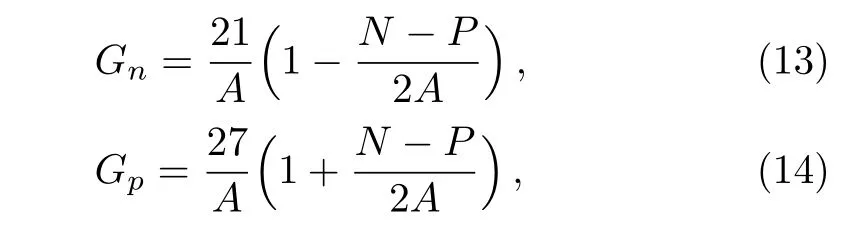
the strength of pairing force is chosen here to reproduce the pairing energy gaps δn,δpin fi nite range droplet model(FRDM),[33]which reproduces all known experimental data of ground state properties and gives good predictions for nuclei far from the β-stable line and the SHN.

3 Numerical Results and Discussions

The ground state properties of nucleus,such as the quadrupole deformation β2,the isotopic shift,two-nucleon separation energy S2n,S2p,one-neutron separation energy S1nand α decay energy Qαfor Z=126 isotope with neutron numbersN=174−244 are calculated by RMF with the e ff ective interaction NL-Z2 parameter sets.Also,the radii distributions are obtained,including rnfor neutrons,rpfor protons,and rc=for charge distribution.

3.1 The Ground State Properties of Isotopes for Z=126 Isotopes

First of all,the binding energy per nucleon has been shown in Fig.1.A relatively good agreement between the present calculations and the results by the FRDM[33]can be oberved.If we check the two curves more carefully,one can find the deviation of the average energy from the two models is evident from neutron numberN=182 to 192.In order to explore this point in the view of systematics,the quadrupole deformation β2of Z=126 isotopes is plotted in Fig.2.It is very clear that the quadrupole deformations by RMF theory are located at about−0.2 from neutron numberN=182 to 192,but the FRDM predicted spherical deformation values for these nuclei.So one can conclude that the ground-state average energy together the deformation are model dependent.It is notable from Fig.1 that the RMF gives the biggest average binding energy at neutron numberN=184,in contrast,which does not emerge on the curve of FRDM calculations.It indicates the proton number Z=126 withN=184 exhibiting an enhanced stability as compared to the neighbors,[23]i.e.,adding more neutrons will not enhance the stability of nuclei with Z=126.On the other hand,in contrast with FRDM,odd-even e ff ect is clearly observed with RMF theory.

Fig.1 (Color online)The binding energy per nucleon BE/A of Z=126 isotopes,using the NL-Z2 interaction in RMF(black square)compared with the FRDM calculations.(red circle).

The isotopic shifts of Z=126 is exhibited in Fig.3.We choose the predicted nucleus310126 with neutron numberN=184 as a reference.However,no obvious kink is observed atN=184.In contrast,a clear kink is obtained atN=208,which is marked with blue dash line as plotted in Fig.3.Interestingly,adding one more neutron atN=208 decrease the size of the nucleus suddenly,implying the large shell e ff ect may exists atN=208 i.e.and the additional neutrons change the distribution of the protons.

Fig.2 (Color online)Quadrupole deformation β2of Z=126 isotopes by using RMF theory(black square)and from the FRDM predictions(red circle).

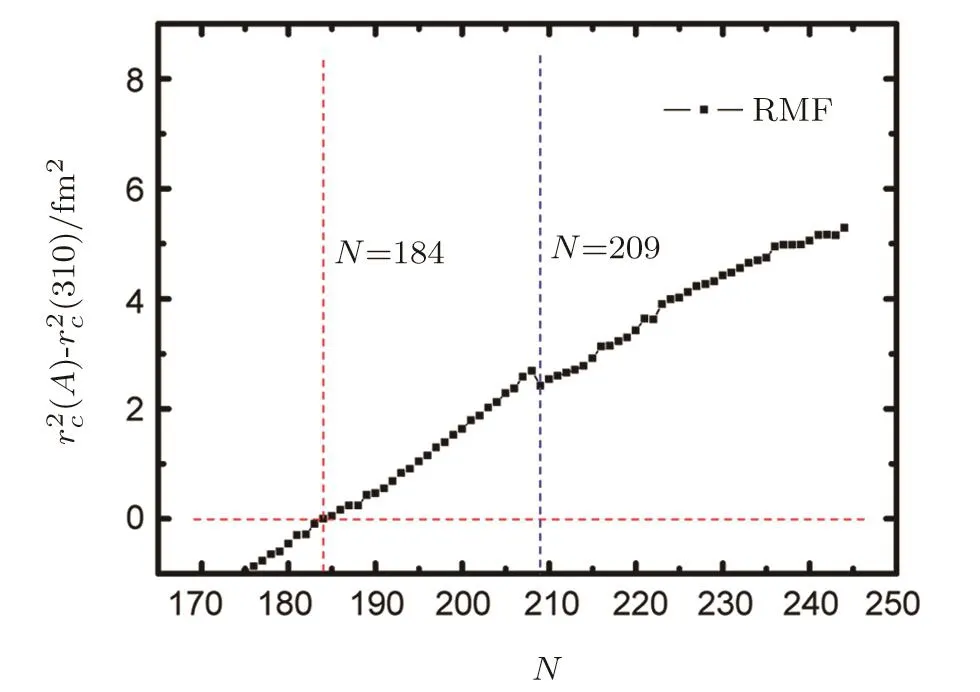
Fig.3 (Color online)The isotopic shifts of Z=126 with respect to a reference nucleus of310126(N=184),which is marked with red lines.

It is clear that both the S1nand S2nobtained from the RMF show a decreasing trend with an increase of the neutron number.The description of the one-neutron separation energy is clearly seen in a good agreement with the calculations from FRDM except atN=182,193,and 201.Comparatively,the kinks atN=182 and 193 calculated by FRDM as we plotted in Fig.4 show an anomalous behaviour according to the odd-even e ff ects,the RMF gives a more eligibility pattern on the contrary.In Fig.4,the calculation obtained from RMF is exhibited as a function of neutron number fromN=175 toN=244,no obvious kink is observed in the region ofN=181−213 from RMF as compared with FRDM,however,a relatively strong kink of S1nexists at neutron numberN=228,which is indicated as a magic neutron number according to Ref.[22],the calculations in the deformation-constrained RMF demonstrate there also exists a large shell gap atN=228 for nuclei with proton number Z=126 in a deformed con fi guration,this kink is reduced as one proceeds to neutron number atN=229.Also,a kink can be seen atN=232,and it vanishes atN=234.The anomalous behaviors indicate the shell e ff ects may exist in this region.

Fig.4 (Color online)One-neutron separation energy S1nfor Z=126 isotopes,the black square denote the calculation obtained from RMF and the red circle denote the FRDM calculation,the data from N=181 to N=213 are compared with FRDM.

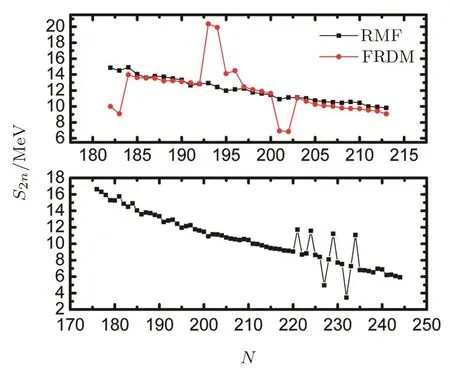
Fig.5 The same as Fig.3,but for two-neutron separation energies of Z=126 isotopes.

Due to the absence of odd-even e ff ects,the S2nvalues obtained by RMF as shown in Fig.5 is better to observe the anomalous behaviour for Z=126 isotopes with neutron numberN=176−244.In general,the RMF and FRDM calculations are consistent with each other.There is no obvious kink in the region ofN=182−220 obtained from RMF,multi-kinks exist atN=220−235 instead.As a whole,if there were attempts for the synthesis of SHN with Z=126,the nuclei with an extremely excess neutrons forN=221,224,229,and 234 are considerable.

It is well known that α decay is the dominant decay mode for heavy and superheavy nuclei.The α decay energies from the RMF calculations for Z=126 isotopes with even neutron numberN=160−212 are plotted in Fig.6,the predictions by FRDM fromN=180 toN=212 are also shown for comparison.The Qαvalues obtained from RMF are by and large gradually reduced with an increase in neutron number,respectively.We choose the even neutron number to neglect the odd-even e ff ect.Thus,a minimum value is clearly seen atN=162,which indicates an enhanced stability as compared to neighbors.A peak emerges atN=164,it diminishes gradually fromN=164 to 188,and the Qαvalues reach the second minimal point atN=188.Such a decrease in Qαvalues leads to an increase of α-decay half-lives by orders of magnitude.It is expected to exhibit an extra stability and long half-lives for Z=126 withN=188.

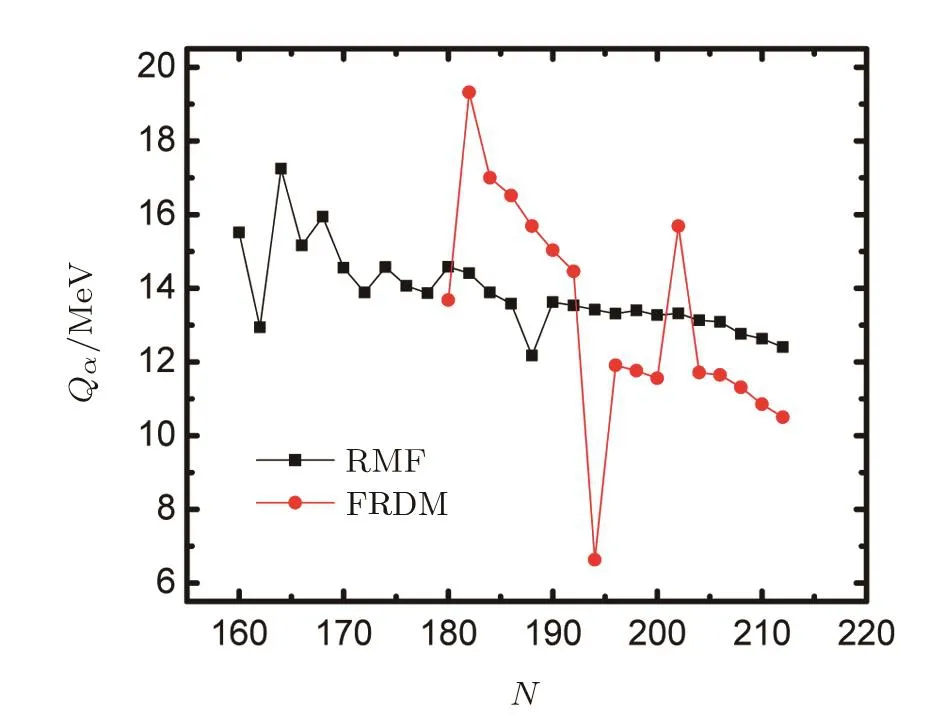
Fig.6 The α decay energies of Z=126 isotopes with even neutron number ranging from 160 to 212,obtained from RMF and FRDM.

3.2 Comparison of the Nuclear Properties between Z=126 and the Neighborly Isotopes

Pairing energy can provide a useful information on the stability of a nucleus.For magic nuclei,single-particle levels up to Fermi energy are fully occupied and hence there is no smearing of the Fermi surface.This implicates that pairing energy should vanish in such cases.Thus the peaks at certain location suggest a magicity of nuclei with speci fic proton or neutron numbers.In Fig.7,we have plotted the proton-pairing energies for even-even nuclei with Z=114−130 as a function of Z obtained from the RMF calculations.An evident peak is observed at Z=120 with the bundles of all the curves except the isotones ofN=162.The value of the pairing energies for protons is very small,which indicates the proton pairing at Z=120 is minimal and it provides a signal for a possible magicity of Z=120.However,as compared to the peak at Z=120,a relatively weak peak is barely seen at Z=126 with all the bundles of curves.Furthermore,according to the trend of these curves as shown in Fig.7,all the curves exceptN=172 isotones start going up at Z=128,we thus surmise an enhanced stability maybe exist at Z＞128.

Fig.7 (Color online)The proton pairing energies for the isotones of N=162,164,166,172 and 184 as a function of even proton number ranging from 114 to 130.

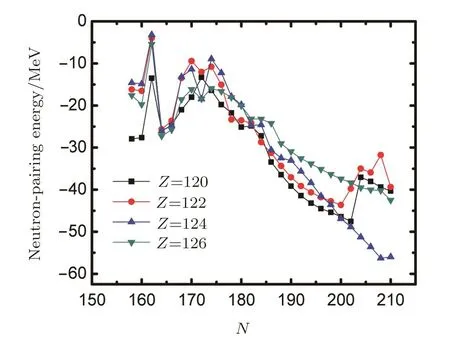
Fig.8 (Color online)The neutron pairing energies for the isotopes of Z=120,122,124,and 126 as a function of even neutron number ranging from 158 to 210.

The neutron-pairing energies are shown in Fig.8.The values of pairing energies for neutron as a function ofNreduce rapidly atN=184,and the pairing energies exhibit extra large values than we expected due to the relative large deformations as shown in Fig.2.In addition to the kink as we can see atN=184,a prominent peak is observed atN=162 for all the isotopes of Z=120,122,124,and 126,which provides an indication for neutron number atN=162 exhibiting a relatively strong magicity.On the other hand,it is noteworthy that a peak can be clearly seen atN=172 only for Z=120 isotopes.Moreover,the peak is also observed from the corresponding pairing energies for proton as we plotted in Fig.7,and it is the highest peak among all the curves.Furthermore,according to the work in Ref.[17],doubly magic spherical nucleus is demonstrated at Z=120,N=172.Now whereby the results as shown in Figs.7 and 8,which provide more evidence for doubly magic nucleus(Z=120,N=172).However,the strong peak is not observed atN=172 for higher proton numbers above Z=120,this implicatesN=172 turns out not to be a strong magic character beyond Z=120.

As shown in Fig.9,the binding energy per nucleon for the isotonic chains ofN=162,164,166,172,and 184 obtained from the RMF calculations decrease gradually with an increase in proton number,generally.Since they start to decrease at Z=114 for neutron numberN=162,164,166,and 172,and it should be noticed that all the curves decrease faster in going down to higher atomic number with increasing neutron number,this emphasizes the predominance of the nuclei with higher neutron numbers,which provides a more enhanced stability with an increase of proton number.Moreover,it is noteworthy that the curves forN=172 andN=184 intersect between Z=120 and Z=122,this indicates the prominent stability forN=184 exhibit above Z=122.On the other hand,in this case,it is noted that all the isotonic chains obtain the highest average binding energies at Z=114,a lot of theoretical predictions and experiments have been made about Z=114,a strong magicity is observed for nuclei with Z=114,and it is clear from Fig.9 that the indication is e ff ective for all the neutron numbers in this case.

Fig.9 (Color online)The binding energy per nucleon for the isotonic chains of N=162,164,166,172,and 184 as a function of even proton number ranging from 114 to 130.

Based on two-nucleon separation energies S2pand S2n,signi ficant information of nuclear structure can also be obtained in the vicinity of Z=126 isotopes.In Fig.10 the S2pvalues show a monotonous decrease with an increase in proton number for all the isotones expect for a kink ofN=162 that can be seen at Z=128.In addition to the kink forN=166,no clear kink is observed at Z=126 for other isotonic curves.On the contrary,a relatively clear kink is obtained at Z=120 forN=172.It is noted that the zero value of S2pis marked with red dashed line in Fig.10,this suggests it is in the vicinity of proton drip line,where the nuclei with(Z=116N=162),(Z=116N=164),(Z=118N=166),(Z=120N=172),(Z=126N=184)are found.On the other hand,a drastic jump of 5.7 MeV is observed forN=162 from 116 to 118,implying Z=116,N=162 is the proton-drip nucleus forN=162 isotones.

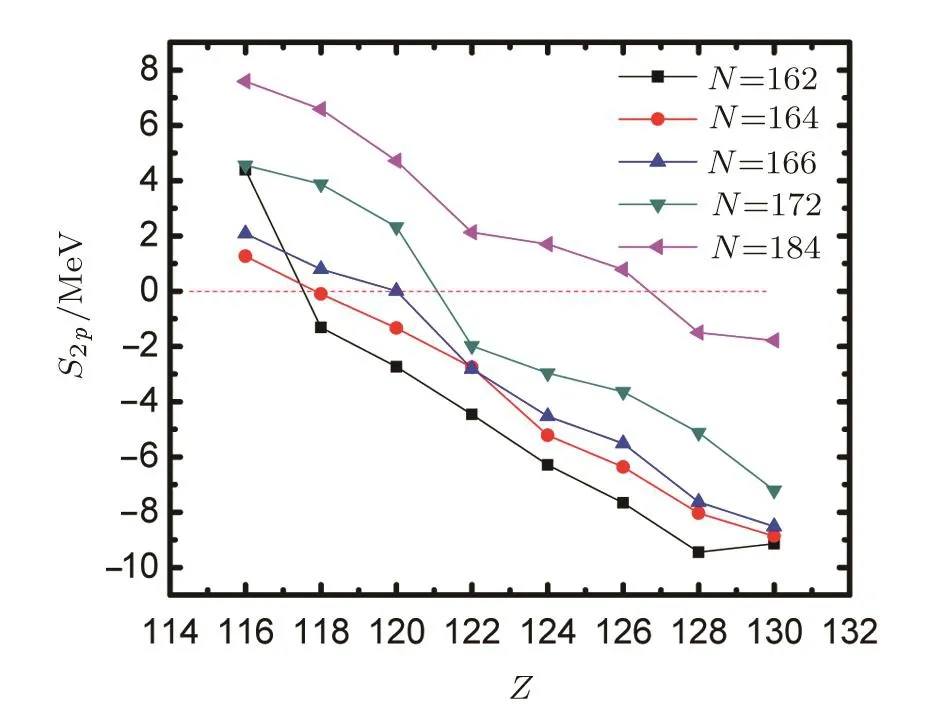
Fig.10 (Color online)The two-proton separation energies for the isotonic chains of N=162,164,166,172,and 184 as a function of Z,ranging from 116 to 130.

In general,S2nvalues show a usual decrease with an increase in neutron number as plotted in Fig.11.However,we do observe some primary kinks in the region ofN=160−174.First of all,a strong peak is shown atN=162 for Z=120−124,which indicates a strong magicity forN=162 as we mentioned before.However,the S2nvalues are observed decreasing fast and drastically fromN=162 to 164,and start going up atN=164,a small peak but not to be neglected emerges atN=166.Another notable kink is observed atN=172,the S2nvalues start going down rapidly atN=172,especially for Z=122 instead of Z=120.In contrast with the kink observed atN=172,the kinks can be seen atN=184 only for Z=122,124,and 126.

To be explicit,we choose310126,304120,292120 as considerable doubly magic nuclei.Instead ofN=162,we chooseN=184 andN=172 as the possible magic neutron number for the reason thatN=162 with Z＞118 is in the vicinity of proton-drip line,it is clearly shown in Fig.10.Since all the results indicate there exists strong shell e ff ect at Z=120 and a relatively weak shell e ff ect at Z=126,it is necessary to explore the microscopic structure and the proton single particle energy levels of these possible doubly magic nuclei are plotted in Fig.12.It is noteworthy that a larger shell gap at Z=126 is observed only in the spectrum of nucleus310126,the values that we marked in Fig.12 are 1.271 MeV for310126,0.361 MeV for304120 and 0.014 MeV for292120.In contrast with the gaps appear at Z=126,the larger gaps at Z=120 are obtained in the nuclei304120,292120 for 2.619 MeV,3.144 MeV,respectively.A large shell gap implicates the shell closure may exist at Z=120.Interestingly,in addition to the large gaps appear at Z=114,120,a clear gap is visible at Z=140,moreover,the value of this gap is even larger than the major shell gap at Z=120 in nucleus304120.

Fig.11 (Color online)The two-neutron separation energies for the isotopic chains of Z=120,122,124,and 126 as a function of N,ranging from 160 to 212.

Fig.12 (Color online)Single particle energy levels of 310126,304120,292120 near the Fermi surface(red dashed lines)for proton,obtained from the RMF calculations within the set of NL-Z2,and the values of notable gap are marked in the interspace between the involved two levels.

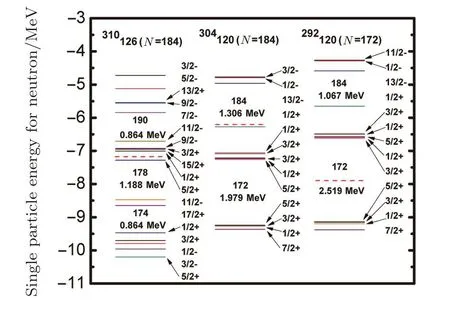
Fig.13 (Color online)Single particle energy levels of 310126,304120,292120 near the Fermi surface(red dashed lines)for neutron,obtained from the RMF calculations within the set of NL-Z2,and the values of notable gap are marked in the interspace between the involved two levels.

The corresponding energy levels for neutrons are shown in Fig.13.It is surprising that there is no clear gap atN=172 or 184 in nucleus310126,since plenty of predictions have been made about the magicity of Z=126(N=184).And a major shell gap is observed atN=178,instead.On the other hand,an evident gap is clearly seen atN=172 and 184 in nucleus304120 as well as292120.Moreover,it is evident that for nucleus with Z=120,the neutron number 172 shows a more reliable shell closure than 184.And in this case,as we plot in Fig.13,the nucleus304120 has the larger shell gaps than that of the nucleus310126.As regards to the Z=120(N=184)and Z=120(N=172),the results indicate that the shell closure has a greater chance to be existing atN=172 rather thanN=184.The other two notable gaps are observed atN=182 in nuclei304120 and292120,these two gaps have almost the same values as we obtained atN=184.Thus we can deduce from the results thatN=184 may be the sub-shell associated with the present RMF calculations.

4 Summary

We have studied the ground state properties of superheavy nuclei of Z=126 isotopes,and for the purpose of comparison,we have also investigated Z=114–130 isotopes with even neutron numbersN=162,164,166,172,and 184 by the RMF theory.The present results from RMF for Z=126 isotopes are reasonably consistent with the FRDM’s predictions generally.The pairing energies provide a good indication of doubly magic nuclei with Z=120,N=172.The neutron-pairing energies and two-neutron separation energies indicate a possible shell closure atN=162.However Z=126 does not show a strong magicity as we expected,but still exhibits additional stability.As a whole,there is not enough evidence to support the magicity of Z=126 as compared to the neighbors in this work,thus the possible magic proton number has a great chance existing at Z=120 rather than Z=126.

References

[1]Ch.E.D¨ullmann,etal.,Nucl.Phys.A 944(2015)1.

[2]W.D.Myers and W.J.Swiatecki,Nucl.Phys.81(1966)1.

[3]H.Meldner,Ark.Fys.36(1966)593.

[4]U.Mosel and W.Greiner,Z.Phys.A 222(1969)261.

[5]D.Ackermann,etal.,Nucl.Phys.A 787(2007)353.

[6]S.Hofmann and G.M¨unzenberg,Rev.Mod.Phys.72(2000)733.

[7]K.Morita,etal.,J.Phys.Soc.Jpn.73(2004)2593.

[8]Yu.Ts.Oganessian,J.Phys.G:Nucl.Part.Phys.34(2007)165R.

[9]Yu.Ts.Oganessian,etal.,Phys.Rev.Lett.104(2010)142502.

[10]Yu.Ts.Oganessian,V.K.Utyonkov,and Yu.V.Lobanov,Phys.Rev.C 79(2009)024603.

[11]B.D.Serort and J.D.Walecka,Adv.Nucl.Phys.16(1986)1.

[12]P.G.Reinhard,Rep.Prog.Phys.52(1989)439.

[13]P.Ring,Prog.Part.Nucl.Phys.37(1996)193.

[14]D.Vretenar,A.V.Afanasjev,G.A.Lalazissis,and P.Ring,Phys.Rep.409(2005)101.

[15]J.Meng,etal.,Prog.Part.Nucl.Phys.57(2006)470.

[16]J.Meng and S.G.Zhou,J.Phys.G:Nucl.Part.Phys.42(2015)093101.

[17]K.Rutz,etal.,Phys.Rev.C 56(1997)238.

[18]A.T.Kruppa,etal.,Phys.Rev.C 61(2000)034313.

[19]G.A.Lalazissis,etal.,Nucl.Phys.A 608(1996)202.

[20]S.Cwiok,J.Dobaczewski,P.H.Heenen,P.Magierski,and W.Nazarewicz,Nucl.Phys.A 611(1996)211.

[21]P.M¨oller and J.R.Nix,J.Phys.G:Nucl.Part.Phys.25(1994)119.

[22]W.Zhang,etal.,Nucl.Phys.A 753(2005)106.

[23]K.Rutz,M.Bender,T.B¨urvenich,T.Schilling,P.G.Reinhard,J.A.Maruhn,and W.Greiner,Phys.Rev.C 56(1997)238.

[24]Zhongzhou Ren,Phys.Rev.C 65(2002)051304(R).

[25]Zhongzhou Ren,Fei Tai,and Ding-Han Chen,Phys.Rev.C 66(2002)064306.

[26]Zhongzhou Ren,Ding-Han Chen,Fei Tai,H.Y.Zhang,and W.Q.Shen,Phys.Rev.C 67(2003)064302.

[27]Hongfei Zhang,etal.,Phys.Rev.C 71(2005)054312.

[28]Y.K.Gambhir,P.Ring,and A.Thimet,Ann.Phys.198(1990)132.

[29]B.D.Serot and J.D.Walecka,Adv.Nucl.Phys.16(1986)1.

[30]J.Boguta and A.R.Bodmer,Nucl.Phys.A 292(1977)413.

[31]Hai-Fei Zhang,etal.,Commun.Theor.Phys.58(2012)544.

[32]Junqing Li,Zhongyu Ma,Baoqiu Chen,and Yong Zhou,Phys.Rev.C 65(2002)064305.

[33]P.M¨oller,J.R.Nix,W.D.Myers,and W.J.Swiatecki,At.Data and Nucl.Data Tables 59(1995)185.