In fluence of Cell-Cell Interactions on the Population Growth Rate in a Tumor∗

2017-05-09YongChen陈勇

Communications in Theoretical Physics 2017年12期

关键词：陈勇

Yong Chen(陈勇)

Center of Soft Matter Physics and its Applications,Beihang University,Beijing 100191,China

School of Physics and Nuclear Energy Engineering,Beihang University,Beijing 100191,China

1 Introduction

The population growth is an important and widespread phenomenon in many areas of knowledge,such as economics,sociology,biology,etc.The growth curves are described by various empirical models by fitting the great variety of statistical data.For instance,the early Malthus model only depending on the number of individuals is of the exponential growth of the human population with small size.[1]With the modi fication with an exponentially decaying growth rate on the original Malthus’s model,the asymmetric sigmoid growth curve of the Gompertz model describes the human lifespan and successfully apply to other biological systems.[2−4]The classical and well- fitting Verhulst model(somewhere named as the Logistic model),in many empirical data(bacterial growth,human population growth,etc.)leads to a logistic growth.[5−7]There are several other models known by the names of the authors,Ricker,Hassell,Beverton–Holt,Maynard–Smith,Richards,Bertalanffy and so on.[8−9]

All the above mentioned phenomenological models are based on the empirical data and only take into account the macroscopic information.It is well known that the macroscopic collective behaviors emerge from the interactions of the microscopic components of the studied systems.Unlike the simple interaction forms in science,the correlation between two living individuals is complicated and is hard to present a quantitative de finition.Mombachet al.recapitulated some well-known models(the Malthus,Verhulst,Gompertz,and Richards models)in the viewpoint of starting from the microscopic properties under the assumptions of the fractal structure and the distance-modulation of the local interaction.[10]After that,Ribeiroet al.presented a further analysis based on physical principle and developed the correspondence between the macroscopic growth rate and the microscopic distance function.[9,11−12]Obviously,this approximation of the interaction between individuals totally ignored the various characteristics of each individual.

Cell colony is a population of cells.Avascular tumor growth as a kind of cell growth is the initial stage of cancer development which is much simpler to construct mathematical models and to realize the quantitative experiments in higher reproducibility.[13−14]The tumor cell only has the following phenotypic states:proliferation,invasion,quiescence,and death.It means that the variety of the cell-cell interactions can be reduced by labeling the cell with its phenotype.Indeed the tumor cell is able to produce the cytotoxic substances against other cells and to in fluence the others by the intracellular chemical communication.[15−18]The simulation results based on the agent-based tumor model shown that the cell-cell interactions can in fluence both the population growth dynamics and the surface roughness.[18−19]We believe that the phenotypic classi fication of the tumor cells is a reasonable and feasible way to model the population growth of a tumor at the level of single cells.

Population growth rate as the basic crucial parameter in population dynamics is the rate at which the number of individuals in a population increases in a given time period.As far as we know,it is rare to study the in fluence of the microscopic individual-individual interaction on this parameter,probably because there is an important difficulty.In this work,we use a simple parameter to measure the effect of the cell-cell interaction on the intrinsic replication rate of the cells in a tumor and present the corresponding sequences of the growth rate.Then,in the case of the avascular tumor,we discuss the modulation of the growth rate by the intracellular phenotype-phenotype interaction.

2 The Model

In general,based on the population balance the number of cells of the typeiin a tumor evolves as the following continuous equation[20]

Here,Sdenotes the source/sink process,andM,P,andDare associated with invasive,proliferative and death phenotypic behaviors,respectively.All the terms on the right-hand side of the above equation are dependent on the locationrand the current functional stateσ.

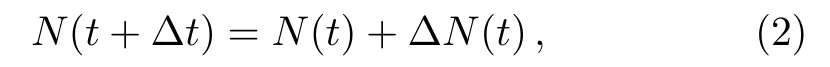
where ΔN(t)is the changes in amount of cell during Δt.For simplicity,ΔN(t)depends on the cellular proliferation and death,PandD,and is proportionate to the population size and the time interval.So,returning to the Eq.(2),we have

HereRis the population growth rate.One takes the limit of in finitesimal Δt,converting the above discrete model(3)to

Essentially,Ris not a simple constant.Based on fitting the statistical population data or considering the microscopical biological processes,several modi fied models have been proposed to describe the population dynamics.The widely used models are known as the Malthus,logistic,Gompertz,Richards-like,Ricker,Hassell model,and so on.[8]All of the models basically are phenomenological descriptions in the macroscopic level.It is known that the collective macroscopic behavior emerges from the interaction of the microscopic components of the system.In this work,we apply the idea of emergent behavior to studying the population growth at the level of the individual cell,especially the contribution of the interaction among the cells to the growth rate.

3 Results and Discussion

3.1 Population Growth Rate and the Intrinsic Replication Rate

For an individual cell,the intrinsic replication rateR0is regulated by a competition between the birth and the death(the tendency to proliferation or death).Mathematically,the intrinsic replication rate of a cell is

wherep0andq0are the proliferative and the necrotic probabilities,respectively.Moreover,note that the probability normalizationp0+q0+m0=1 andm0is the probability for others functional states of the cell,such as migration,invasion,quiescence,etc.

The update of the population obeys the following equation,

whereρc(r,t)is the spatial distribution of the cells at timet.Note thatR=R0in the above equation is only valid for the intrinsic replication of the cells.

Clearly,the in fluence of the interaction among the cells on the population growth rateRis the inevitable objective fact.For simplicity,we usep=gp0to describe the resulting proliferative probability which includes the intrinsic probability and the local environmental in fluences.This simpli fication is realistic since all the external in fluences finally appear as the intracellular biological processes.The parametergis larger than 0.g=1 denotes the case without the contribution of the local field.g＜1 means the interaction among the local cells is competitive,andg＞1 is for the cooperation.Thus,the resulting replication rate of the individual cell of the population is

It is obvious that the resulting rateRis reduced toR0forg=1.

Figure 1 presents the dependences of the resulting replication rateRon the intrinsic proliferative probabilityp0and the parameter describing the interactions among the cellsgunder several intrinsic replication rates of the individual cellR0.The range ofp0depends on the value ofR0and it followsp0∈[R0,(R0+1)/2].Note that the horizontal axis is the data ofgin logarithmic coordinates.

The lines ofg=1 divide the phase diagrams into two parts,the left cooperation region,and the right competition region.In all cases of cooperation(g＞1),the intrinsic proliferative probabilityp0has no obvious in fluence on the final replication rateR,especially in the region of largerR0andp0.It only plays little role in the case of very smallR0andp0(see Fig.1(a)).However,increasinggis effective for improving the resultingRand is efficient in cases of smallerR0and largerp0.The left competition part in Fig.1(g＜1)is much different than the right one.First,there exists a contour line withR=0 which divides the left part into two regions,the bottom left region of population decrease(R＜0)and the upper right region of population growth(R＞0).As a result,it is possible that the tendency of population variation will switch over by changingp0org.Interestingly,there is a minimum value ofp0and the variation tendency cannot be changed ifp0is smaller than it.For stronger competition from local field(smallerg),the role ofp0regulatingRbecomes remarkable.Similarly,gis much more efficient in the cases of smallerR0and largerp0.Comparatively speaking,in most cases(in the vicinity ofg=1),changinggis a more feasible and efficient solution to regulate the resulting replication rateR.

Fig.1 Contour graphs of the population growth rate R involving the contribution from cell-cell interactions g for different intrinsic growth rates(a)R0=0.1,(b)R0=0.3,(c)R0=0.5,and(d)R0=0.8.

3.2 Population Growth Rate in An Avascular Tumor

All tumor progression undergo a stage of avascular growth.The main feature of avascular tumors is composed of a necrotic core of dead tumor cells due to nutrient starvation and an outer proliferative rim with abundant nutrient environment.[13,20]In another word,there is almost no necrotic cell in the outer rim of the avascular tumor.According to the de finition of the replication rate in Eq.(5),the population sizeNin Eq.(6)is the total number of the alive cells.Thus,it is feasible to assumeq0≃0 andR0≃p0since the growth rate of avascular tumor is determined by the growth of non-necrotic outer rim.One can rewrite the resulting replication rate in expression(7),

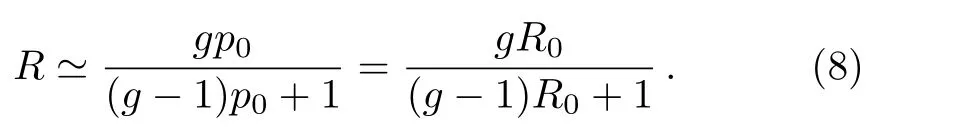
The equation above presents there is no dead cells in the local interaction field.

The interaction parametergobviously is associated with a number of factors,such as the local cell number density,the nutrient concentration,the cellular functional state,and so on.Inspired by the packing structure in solid crystal,we consider the contribution of the nearest neighbor cells on the local interaction.The interaction parameter will have the form[18−19]

Here,αi∈(−1,1)denotes the interaction between two proliferative cells andβj∈(−1,1)describes the interaction between a proliferative cell and another cell with other phenotypes.Note that the mutual interaction between two cells normally brings into effect by the autocrine/paracrine growth factor,the cytotoxic substance,the chemical communication,etc.and the linking genotypes are complex.N0presents the total number of the nearest neighbor cells. For example,N0=6 for two-dimensional triangel structure and 12 is for threedimensional hexagonal close-packed(HCP)scenario.Furthermore,neglecting the cell type diversity and assuming thatαi=αandβj=β,the interaction parameter in Eq.(9)can be approximated by

Substituting the expressiongabove to Eq.(8),we obtain the dependence of the growth rateRon the different cell-cell interactionsαandβas shown in Fig.2.In all cases,R＞0 means a population growth process since the approximation the death probabilityq0=0 in the proliferative rim of the avascular tumor.Bothα＞0 andβ＞0 denote the cooperative interactions.

Actually,based on Eq.(9),one can find changingαorβwill make a similar in fluence onRwhich is shown in Fig.2(c).The stronger the positive/negativeα(β),the larger/smallerR.In the extreme case of very low intrinsic replication rate(R0is very small illustrated in Fig.2(a),only the interaction between the proliferative cell and the cell at other functional statesβhas a remarkable cooperative in fluence onRbecause of the much smaller amount of the proliferative cell.In another extreme case ofRclose to 1(see Fig.2(d),the interaction between two proliferative cellsαis effective to suppressRbecause it has plenty of proliferative cells.

Fig.2 Contour graphs of the population growth rate R involving the contributions of the combination of two kinds of cell-cell interactions α and β for different intrinsic growth rates(a)R0=0.05,(b)R0=0.25,(c)R0=0.5,and(d)R0=0.95.Here,we choose N0=6 for two-dimensional avascular tumors.

4 Conclusion and Remarks

In this work,we study the in fluence of the cell-cell interactions on the population growth rate in the level of the individual cell.By integrating the interaction from the surrounding of the cells into the changing of the intrinsic replication rate,we present the dependence of the resulting replication rate on the proliferative probability and the cell-cell interactions.It is found that the in fluence of the local field is remarkable for large intrinsic replication rate and proliferative probability.Moreover,in most cases changing the interaction between the cells is a more feasible recipe to regulate the population growth rate.Under the nearest neighbor approximation in the outer rim of two-dimensional avascular tumors,we divide the cell-cell interactions into two classes and conjecture that the local cell number density is crucial to in fluence the resulting replication rate.

Rigorously,the population growth rateRin Eq.(6)is the replication rate of an individual in a population and is not the exact equivalent of the per-capita population growth rateRin Eq.(4).The distribution of the cellsρc(r,t)can be described by the fractal structure,or be solved by the continuous descriptions,such as the reaction-diffusion model,two-phase model,and so on.[13,20,23]By using Eqs.(7),(9),and solving Eq.(6),one will obtain the population growth equation and the per-capita growth rate.

It is should be noted that the cell-cell interactions in present work can be used to study the other similar systems with a lot of individuals.The results presented in this work will cast some light on explaining the collective phenomena induced by the individualindividual interaction properties in a more fundamental way.

[1]T.R.Malthus,An essay on the Principle of Population as It Affects the Future Improvement of Society,J.Johnson,London(1798).

[2]R.Gompertz,Phil.Trans.R.Soc.Lond.115(1825)513.

[3]J.L.Haybittle,Int.J.Epidemiol.27(1998)885.

[4]M.Ausloos,Adv.Complex Syst.15(2012)1250088.

[5]P.F.Verhulst,Corr.Math.Phys.X(1838)113.

[6]P.F.Verhulst,Nouveaux memoires de l’Academie Royale des Sciences et Belles Lettres de Bruxelles 18(1845)1.

[7]P.F.Verhulst,Nouveaux memoires de l’Academie Royale des Sciences et Belles Lettres de Bruxelles 20(1847)1.

[8]D.S.Boukal and L.Berec,J.Theor.Biol.218(2002)375.

[9]R.V.dos Santos,F.L.Ribeiro,and A.S.Martinez,J.Theor.Biol.385(2015)143.

[10]J.C.M.Mombach,N.Lemke,B.E.J.Bodmann,and M.A.P.Idiart,Europhys.Lett.59(2002)923.

[11]F.L.Ribeiro,B.Math.Biol.77(2015)409.

[12]F.L.Ribeiro,First Principles Attempt to Unify some Population Growth Models,arXiv:1605.06309v1.