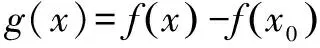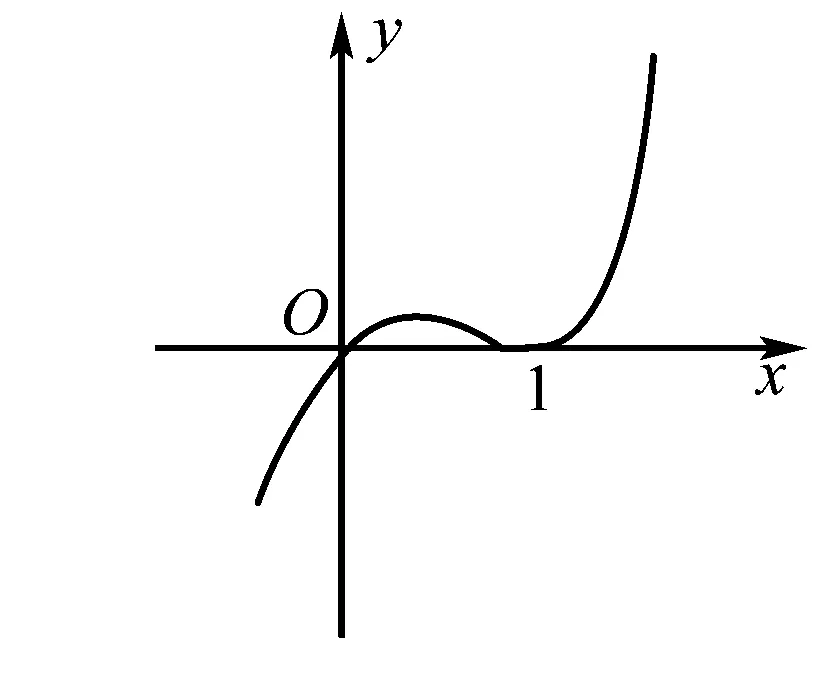零点与极值点重合之后
2017-05-17浙江省桐乡第二中学314511范广法
浙江省桐乡第二中学(314511) 范广法●
零点与极值点重合之后
浙江省桐乡第二中学(314511)
范广法●
本文重点介绍了一类函数的零点与极值点重合时的一个结论,并结合高考实例给出常见应用.
零点与极值点重合;结论
用穿针引线法解高次不等式时,若遇到重根时则要求“奇穿偶不穿” .如设f(x)=x(x-1)2(x-2)3,意思是说:由于2是方程f(x)=0的奇数重根,在x=2附近函数y=f(x)的图象要穿透x轴;而1是方程f(x)=0的偶数重根,在x=1处函数y=f(x)的图象碰到x轴后立刻反弹,而不是穿透,俗称“穿而不透”.结合穿针引线法所画函数y=f(x)的图象不难发现,1既是函数y=f(x)的极值点又是零点,推而广之后有:

一、“式”“图”结对研判图象
例1 (2009年安徽高考)设a 解析 (x-a)2是函数y=(x-a)2(x-b)的因式,这是已知函数在“式”上的特征,又a 上述结论中的x0及例1中的a都具有双重身份——y=f(x)的极值点、零点,有时只要抓住这一点就可化解参数取值. 例2(2016年浙江高考)设函数f(x)=x3+3x2+1.已知a≠0,且f(x)-f(a)=(x-b)(x-a)2,x∈R,则实数a=____,b=____. 解析 首先明确参数a,b的身份,设g(x)=f(x)-f(a)=(x-b)(x-a)2,g(x)与f(x)的图象存在上下平移关系,所以非零实数a是g(x)的极值点(当然也是f(x)的极值点)、零点,b是g(x)的另外一个零点,这样实数a,b的身份就清楚了.其次化解参数a,b的取值,又f(x)=x3+3x2+1的极值点是-2、0,所以非零实数a=-2,从而g(x)=f(x)-5=(x-b)(x+2)2,令x=0求得实数b=1. 例3 (2016年天津高考)设函数f(x)=x3-ax-b,x∈R,其中a,b∈R.若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=0. 例4 (2012年浙江高考)设a∈R,若x>0时均有[(a-1)x-1](x2-ax-1)≥0,则a=____. 解析 设f(x)=[(a-1)x-1](x2-ax-1),当x→+时,x2-ax-1>0,f(x)≥0,必有(a-1)x-1≥0,所以a-1>0.而x>0时f(x)=0有两正根.要使得x>0时f(x)≥0恒成立,考虑到穿根的特点,两正根必相等,所以具有双重身份——f(x)的极小值点、零点,,从而求得. 例2例3中都有“x∈R”,这表明给定的式子是恒成立的,从此入手也可化解参数难题. 例5 (同例3) 解析二f(x)-f(x0)=(x-x1)(x-x0)2.因为f(x0)为常数且x∈R,所以f′(x)与[f(x)-f(x0)]′恒等,即3x2-a与(x-x0)(3x-x0-2x1)恒等,再求导有6x与6x-4x0-2x1恒等,比较两边的常数项有0=-4x0-2x1即x1+2x0=0. 4.利用取值画图,研判极值点类型 上述结论不能研判x0是极大值点还是极小值点,如若研判极值点类型,可参考以下两例. 例6 (2013年浙江高考)已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则 A.当k=1时,f(x)在x=1处取到极小值 B.当k=1时,f(x)在x=1处取到极大值 C.当k=2时,f(x)在x=1处取到极小值 D.当k=2时,f(x)在x=1处取到极大值 解析一 当k=1时,f(x)=0只有两解0,1,由穿针引线法可作出函数f(x)的大致图象,排除A,B;当k=2时,f(x)=0只有两解0,1(二重根),由穿针引线法可作出函数f(x)的大致图象(见图),易知只有选项C正确. G632 B 1008-0333(2017)10-0018-01
二、明确身份特征,化解参数取值
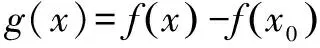
三、利用恒等原理,化解参数取值