基于对推理与证明的高考考点分析

安徽省利辛高级中学(236700) 陈国林●

赣南师范大学科技学院(341000) 寇桂晏●



基于对推理与证明的高考考点分析

安徽省利辛高级中学(236700)
陈国林●

赣南师范大学科技学院(341000)
寇桂晏●

推理证明是教材内容的亮点之一，它需要的是一个思想过程，其中推理部分主要从合情推理和逻辑推理进行考查，证明部分主要从综合法、分析法和反证法、放缩法、数学归纳法去考查学生的逻辑思维能力.

考点一 合情推理

例1 (2008全国卷2)平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：

充要条件①____；

充要条件②____．

解析 四棱柱为平行六面体的充要条件可以由四棱柱与平行六面体的定义加以条件强化即可，如下面可得一些充要条件：两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点且互相平分等．(答案不唯一)

评注 合情推理：归纳推理和类比推理都是根据已有事实，经过观察、分析、比较、联想在进行归纳.因此在求解此类问题时，需要与已经熟知的内容进行类比分析，得出结论.

考点二 逻辑推理

例2 (2016年新课标卷)有三张卡片，分别写有1和2，1和3，2和3．甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是 2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是____．

考点三 反证法

例3 (2016届湖北省武汉市武昌区高三5月调研)

(1)求a+b的值；

(2)证明：a2+a>2与b2+b>2不可能同时成立．

解析 (1)∵a>0,b>0，

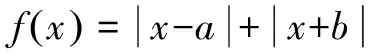
∴ab≤1．

假设a2+a>2与b2+b>2同时成立，则由a2+a>2及a>0，得a>1．

同理b>1，∴ab>1，这与ab≤1矛盾．

故a2+a>2与b2+b>2不可能同时成立．

评注 利用反证法一般情况是推导过程中出现矛盾，或者和已知问题的条件矛盾，进而证明原结论成立.

考点四 综合法

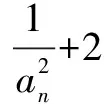
评注 综合法的运用是根据由已知条件和某些定理及题目中的已知信息进行推理论证，最终得到需要证明的结论.

考点五 分析法

例5 (2016届黑龙江省哈尔滨三中高三三模)已知函数f(x)=|2x-1|+|x+2|.

(1)求函数f(x)的最小值a；

评注 对于较复杂陌生式子的证明，我们可以先对它进行一些等价变形，直到化为简单熟悉的形式，再证明这个变形后的式子成立.

题型六 数学归纳法

下面用数学归纳法证明②．

(1)当n=1时，左边=右边=2，②成立．

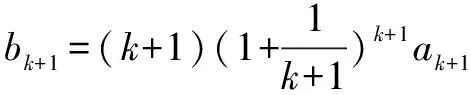
所以当n=k+1时，②也成立．

根据(1)(2)，可知②对一切正整数n都成立．

评注 数学归纳法有很多种，中学阶段一般考查第一数学归纳法.数学归纳法的一般步骤为(1)证明当n取第一个值n0时命题成立；(2)假设当n=k(k≥n0，其中k是自然数)命题成立，证明当n=k+1时命题也成立.

题型七 放缩法

解析 (1)略.

(2)当n=1时，结论显然成立；当n≥2时，

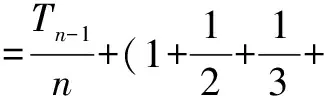
Sn=b1+b2+…+bn

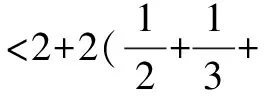
所以f(x)

G

B

1008-0333(2017)10-0016-02