超高斯随机振动疲劳加速试验模型研究

蒋 瑜， 陶俊勇， 陈 循

(国防科技大学 机电工程与自动化学院装备综合保障技术重点实验室， 长沙 410073)

超高斯随机振动疲劳加速试验模型研究

蒋 瑜， 陶俊勇， 陈 循

(国防科技大学 机电工程与自动化学院装备综合保障技术重点实验室， 长沙 410073)

通过理论分析，针对超高斯随机振动激励建立了相应的振动疲劳加速试验数学模型，给出了模型中未知参数的具体求解方法，并通过实际试验进行了验证。该模型十分便于进行振动疲劳加速试验的定量设计，具有很好的工程实用性，可用于评估随机振动环境下工程结构的疲劳寿命与可靠性。

超高斯； 随机振动； 振动疲劳； 加速模型

振动引起的疲劳问题作为多个工程领域广泛存在的一个共性问题，严重危及重大装备及结构的可靠性和安全性。如果能够提前准确预测结构的振动疲劳寿命，就能在发生灾难性事故之前及时预知并采取相应的措施，并可为其定寿、延寿提供科学的依据，最大限度地发挥装备效益。因此，准确预测重大装备和工程结构在复杂随机动态载荷作用下的振动疲劳寿命是提高其可靠性和安全性的关键技术，被国家自然科学基金委员会列入《机械工程学科发展战略报告(2011～2020)》。

当前工程中进行结构振动疲劳寿命分析和预测时，由于缺乏充分的认识和解决相关问题的工具及方法，通常假设结构承受的随机载荷符合平稳高斯分布。但是，在实际环境中，上述许多随机载荷往往呈现比较明显的非高斯特征，尤其是在工况恶劣或者极端环境下。近年来的一些研究结果表明，随机载荷的非高斯特性对结构振动疲劳有着不可忽视的影响，某些情况下会加速结构的疲劳失效。基于高斯假设计算振动疲劳损伤往往会得到偏大的振动疲劳寿命估计结果，给装备服役或使用阶段埋下巨大的安全隐患。

同时，随着结构可靠性水平的提高，结构的振动疲劳寿命越来越长，为了能够在实验室验证其寿命是否达到要求，加速试验成为必然的选择。要想通过加速试验得到结构在实际服役振动环境下的疲劳寿命，正确的加速试验统计模型是关键。国内外目前关于振动加速试验模型的研究不多，尤其是对非高斯随机振动加速试验。王冬梅等[1]对振动加速试验的逆幂律模型进行了推导，探讨了其适用范围，指出其适用于窄带高斯载荷，不适用于宽带高斯和非高斯载荷。李奇志等[2]提出通过试验的方式获得振动试验的加速因子，认为振动加速试验的逆幂律模型对平稳窄带和宽带高斯随机过程均是适用的。朱学旺等[3]应用基于窄带模型的修正方法得到了宽带随机振动试验加速因子计算的通用表达式，认为基于窄带模型的加速因子表达式对于比例载荷的宽带随机振动也是适用的，而对于非比例载荷，则需要应用其提出的通用表达式才可以获得。Allegri等[4]研究了适用于平稳宽带高斯随机振动加速试验的逆幂律模型，其主要目的是用来评估相对疲劳损伤，而非用来精确预计寿命。Pothula[5]研究了附着不同阻尼材料的铝合金梁在高斯随机振动加速试验中的疲劳寿命差异，探讨了结构阻尼对振动试验加速因子的影响。John[6]提出应用Fatigue Damage Spectrum(FDS)来进行振动加速试验设计与评估，但是只考虑了振动激励的功率谱密度PSD (Power Spectral Density)，只适用于高斯振动加速试验。

总的来说，目前国内外开展的振动疲劳加速试验研究主要针对高斯振动，尤其是实际进行的非高斯振动加速试验很少，需要进一步探索适用于非高斯随机振动的疲劳加速试验定量模型。

1 理论分析

工程上常用偏斜度S和峭度K这两个参数来描述非高斯随机过程X，定义为

(1)

高斯随机过程的偏斜度值等于0，峭度值等于3；而非高斯随机过程的峭度值肯定不等于3，偏斜度值可以等于零也可以不等于0。偏斜度用来描述随机过程幅值概率密度曲线偏离对称分布的程度，偏斜度值不为零表示服从非对称分布。峭度是描述随机过程幅值概率密度曲线拖尾分布特征的参数，它不仅可用来区分高斯和非高斯随机过程，而且还可进一步将非高斯随机过程区分为亚高斯和超高斯随机过程，其中亚高斯随机过程的K<3，超高斯随机过程的K>3。工程中常见的非高斯振动信号往往是具有尖峰分布的对称超高斯信号，因此本文研究的非高斯振动疲劳主要针对超高斯。

1.1 高斯振动疲劳加速试验模型

首先，从最基本的描述材料疲劳现象的S～N曲线出发。通常理想的S～N曲线的数学表达式为

N=cS-b

(2)

式中：S为应力幅值；N为引起失效的应力循环次数；b、c为材料双对数S～N曲线中的常数，且b的取值范围一般为6～25。

根据著名的疲劳损伤累积Miner准则，不同幅值应力共同作用下造成的疲劳损伤为

(3)

式中：ni是幅值为Si的应力作用循环次数；Ni为试件在幅值为Si的应力作用下至疲劳失效的循环次数；D为累积疲劳损伤(一般认为当D=1时发生疲劳失效)。

将式(2)代入式(3)可得

(4)

对于连续的随机应力时间历程，式(4)可写成如下积分的形式[7]

(5)

当随机应力响应接近平稳窄带高斯分布时，根据随机过程理论，应力幅值概率密度函数p(S)将近似服从瑞利(Rayleigh)分布

(6)

式中：σS为应力的均方根值(即标准差)。将式(6)代入式(5)进行积分可得

(7)

式中，Γ为Gamma函数。

进行振动试验的产品或试件一般可近似看成一个线性系统，而振动试验设备产生的振动激励可看作该系统的输入。工程实践表明，一般结构件的阻尼比ξ通常远小于1，可以取到0.05以下这样小的值。根据文献[8]，在满足小阻尼线性系统的假设前提下，σS的近似计算式为

(8)

式中：f1为试件结构的一阶固有频率；ξ为等效的阻尼比(一般假设ξ≤0.1)；k为与试件材料相关的比例常数；Ga(f1)为输入振动激励的加速度功率谱密度在试件固有频率f1处的量值。

(9)

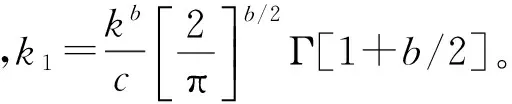
由于试件结构的传递函数一般都类似一个窄带滤波器，因此可以认为试件在平稳高斯随机激励作用下(无论是宽带还是窄带)，其应力响应为平稳窄带高斯分布，可以采用式(9)来估计其疲劳累积损伤。

一般认为D=1时结构发生疲劳失效，根据式(9)可得高斯随机振动激励下的结构振动疲劳寿命TG为

(10)

对常用工程材料，b的取值范围一般为4～25。从式(10)可以看出，对高斯随机振动激励，当结构动力学特性参数如f1、ξ固定时，结构振动疲劳寿命T与高斯随机振动激励的功率谱密度在结构一阶固有频率处的量值大小Ga(f1)成反比关系。随着Ga(f1)的增加(或减小)，T按指数规律迅速衰减(或增长)。

根据式(10)进一步可得a1、a2两种不同高斯随机加速度激励下的结构振动疲劳寿命分别为

(11)

(12)

根据式(11)和式(12)可得

(13)

显然，式(13)就是传统文献中用于描述高斯振动加速试验的逆幂律模型。从上述推导过程来看，只要工程结构系统的频响函数是一个窄带滤波器(实际中大多数工程结构均满足这一条件)，并且结构随机响应服从高斯分布，则就可以运用式(13)对振动加速试验进行建模。因此，式(13)只适用于描述高斯振动疲劳加速试验，下面继续讨论非高斯振动疲劳加速试验模型。

1.2 超高斯振动疲劳加速试验模型

当随机应力响应接近平稳窄带非高斯分布时，可考虑在式(9)的基础上增加一个非高斯修正因子λ来描述应力响应的峭度值对振动疲劳累积损伤的影响

(14)

非高斯修正因子λ和应力响应的峭度值Ks直接相关，可用式(15)来描述

(15)

式中，参数α为比例系数。

显然，当应力响应为高斯即Ks=3时，λ=1，式(14)变成式(9)；当应力响应为超高斯即Ks>3时，λ>1，意味着应力响应的超高斯特性会加快疲劳累积损伤进程。

下面根据随机振动理论分析影响应力响应峭度值Ks的因素。由于结构的一阶模态对结构响应起决定性作用，因此建立振动台基础激励作用下的单自由度系统模型进行分析，如下图1所示。

经过推导可得加速度响应y与振动台台面的基础加速度激励x之间的传递函数为

(16)

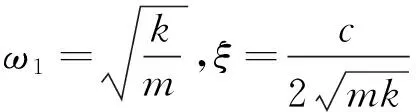
(17)

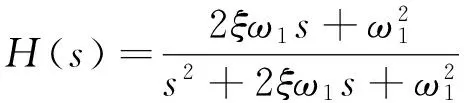
(18)

式中：ω1=2πf1，f1为试件结构的一阶固有频率；ξ为阻尼比。这两个参数表征了试件结构本身的动力学特性，并且试件结构系统的通频带BWH也由这两个参数决定，即

BWH=2ξf1

(19)

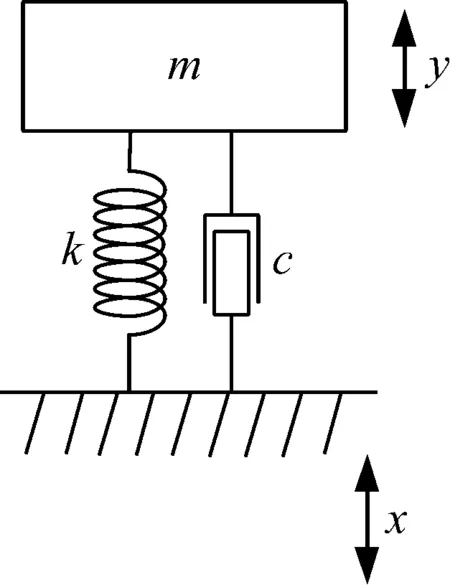
图1 振动台基础激励作用下的单自由度模型

由于实际工程结构的阻尼比ξ往往较小，而一阶固有频率f1往往不大，所以大多数工程结构的通频带BWH往往也不大，也就是说可以视为一个窄带滤波器。

下面先对响应带宽进行分析。设激励x的功率谱密度记作X(f)，响应y的功率谱密度记作Y(f)，系统频响函数为H(f)。根据线性系统和随机过程理论有

(20)

由此容易得出响应的有效频谱带宽

(21)

接下来讨论非高斯激励下结构响应的幅值分布特性。随机过程x(t)通过线性系统H(f)后的输出在时域可表示为

(22)

式中，h(t)为系统H(f)的冲击响应函数，上述积分可用极限和形式表示，即

(23)

式中：x(τk)为随机变量；Δτk为取样时间间隔。根据中心极限定理，大量统计独立的随机变量之和的分布趋于高斯分布。如果输出随机过程y(t)在任意时刻t上皆为大量独立随机变量之和，则y(t)便接近于高斯分布。显然这里要求两个条件：一个是随机变量必须相互独立，另一个是独立随机变量要累加求和。

现在来考虑第二个条件。众所周知，当宽带随机信号作用于窄带系统(如图10所示滤波器频响结构)时，由于系统有惰性，不能立即对信号作出响应，它需要一定的建立时间ts，而ts与系统带宽BWH成反比，即ts∝1/BWH。这样，BWH越小，则ts越大，对信号响应的时间越长，对随机输入各个取样(随机变量)累积时间也越长，于是当各个取样相互独立，且累积时间又足够长，即满足ts≫Δτk时，则y(t)趋于高斯分布。反之，若非高斯随机过程作用于线性系统，而系统的通频带较宽时，这时ts较小，若小到ts≪Δτk，则输入随机过程通过系统后失真很小，于是输出随机过程y(t)的分布将接近原输入随机过程x(t)的分布，即为非高斯分布。

综上所述，当τx≪Δτk≪ts时，或简化为τx≪ts时，系统在非高斯随机输入下，其输出接近高斯分布。由于τx∝1/BWX及ts∝1/BWH，因此τx≪ts也就意味着BWX≫BWH。于是上述结论又可表述为线性系统输入随机过程的有效频谱带宽远大于系统带宽时，输出随机过程的幅值分布将趋于高斯分布，而与输入随机过程是否为高斯分布无关；换言之，当输入随机过程的有效频谱带宽接近或小于系统带宽时，如果输入是非高斯分布则系统输出也将为非高斯分布。

根据上述分析结论，可采用下式来描述应力响应的峭度值Ks和加速度激励的峭度Ka、带宽BWa以及结构本身的带宽BWH之间的关系

(24)

式中，参数β为比例系数。

综合式(15)和式(24)可得非高斯修正因子λ的表达式为

(25)

从式(25)可以看出，非高斯随机振动激励的峭度和带宽对结构应力响应的非高斯特性影响比较明显，从而对结构的振动疲劳寿命也会产生明显影响。

将式(25)代入式(14)，并令D=1，可得非高斯随机振动激励下的结构振动疲劳寿命TNG为

(26)

令ε=αβ，则式(26)可进一步简化为

(27)

有了式(27)，就可以将结构振动疲劳寿命与振动激励的诸多特性以及结构本身动力学特性都紧密地联系起来，用于定量设计振动加速试验将十分方便。

从式(27)可以看出：一旦确定了试件结构的材料、外形和尺寸，f1、ξ和BWH也随之确定，可视为已知量；一旦确定了振动激励，Ga(f1)和BWa也随之确定，也可以视为已知量。这样，式(27)中还有3个未知量待求：b、k1和ε。下面依次探讨这3个未知量的求解方法。

首先讨论如何求解参数b。

对式(13)两边取对数，可得

(28)

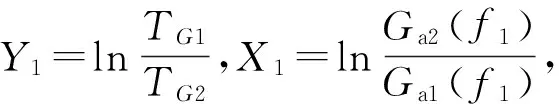
(29)

这样就可以通过进行几组高斯随机振动试验，得到若干组(X1,Y1)的值，然后进行曲线拟合，就可以得到参数b的估计值。

接下来讨论如何求解参数k1。

对式(10)进行变换可得

(30)

Y2=k1X2

(31)

同样，根据几组高斯振动疲劳试验的结果，得到若干组(X2,Y2)的值，然后进行曲线拟合，就可以得到参数k1的估计值。

最后讨论如何求解参数ε。

对式(27)进行变换可得

(32)

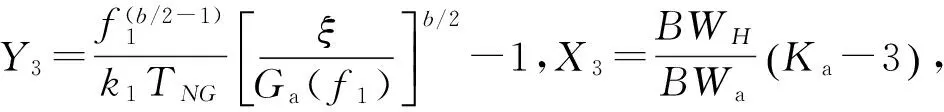
Y3=εX3

(33)

这样可以通过进行几组非高斯随机振动试验，可以得到若干组(X3,Y3)的值，然后进行曲线拟合，就可以得到参数ε的估计值。

至此，就求出了式(27)中所有的未知参数，从而就可以预计出不同试验条件下的结构振动疲劳寿命，并可据此推断出试件在某实际服役振动环境下的疲劳寿命。

2 试验研究

2.1 试验对象

某型变压器电子组件在振动环境下其电容管脚容易出现疲劳断裂，如图2所示。

(a)

(b)

2.2 试验方案及结果

根据前述参数估计方法，分别设计了一组高斯和一组超高斯振动疲劳试验，如表1和表2所示。其中高斯振动疲劳试验结果用于估计参数b和k1，超高斯振动疲劳试验结果用于估计参数ε。在得到三个未知参数的估计值后，再选择如表3所示的试验条件进行试件的常规寿命试验，并与采用疲劳加速试验模型预测的结果进行比较。

表1 高斯振动疲劳试验

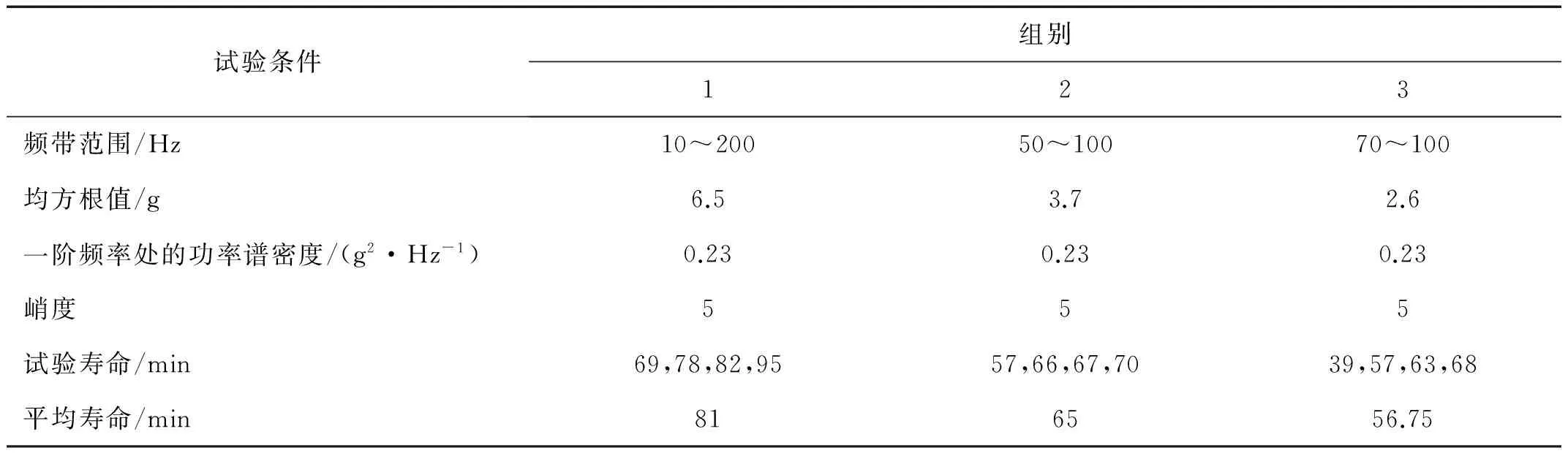
表2 超高斯振动疲劳试验

表3 疲劳寿命预测验证试验

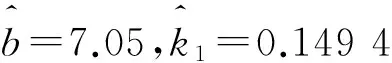
3 结 论

本文通过理论分析，提出了一种能够适用于超高斯随机振动加速试验的数学模型，并给出了模型中未知参数的具体求解方法。该模型系统全面地将结构振动疲劳寿命与振动激励的诸多特性以及结构本身动力学特性都紧密地联系起来，用于指导超高斯振动疲劳加速试验剖面的定量设计将十分方便，具有很好的工程实用性。

[1] 王冬梅, 谢劲松. 随机振动试验加速因子的计算方法[J]. 环境技术, 2010, 28(2): 47-51.

WANG Dongmei, XIE Jinsong. Acceleration factor calculation method of random vibration test[J]. Environment Technology, 2010, 28(2): 47-51.

[2] 李奇志, 陈国平, 王明旭, 等. 振动加速因子试验方法研究[J]. 振动、测试与诊断, 2013, 33(1): 35-39.

LI Qizhi, CHEN Guoping, WANG Mingxu, et al. Test method of vibration acceleration factor[J]. Journal of Vibration,Measurement&Diagnosis, 2013, 33(1): 35-39.

[3] 朱学旺, 张思箭, 宁佐贵, 等. 宽带随机振动试验条件的加速因子[J]. 环境技术, 2014(6): 17-20.

ZHU Xuewang, ZHANG Sijian, NING Zuogui, et al. Accelerated testing factor on wideband random vibration[J]. Environment Technology, 2014(6):17-20.

[4] ALLEGRI G, ZHANG X. On the inverse power laws for accelerated random fatigue testing[J]. International Journal of Fatigue, 2008, 30(6): 967-977.

[5] POTHULA A, GUPTA A, KATHAWATE G R. Fatigue failure in random vibration and accelerated testing[J]. Journal of Vibration and Control, 2012, 18(8): 1199-1206.

[6] JOHN V B. Fatigue damage spectrum—a new tool to accelerate vibration testing[J]. Sound and Vibration, 2015, 49(3): 15-17.

[7] CRANDALL S H, MARK W D. Random vibration in mechanical systems[M]. New York: Academic Press, 1963.

[8] KERN D L. Dynamic environmental criteria: NASA-HDBK-7005[S]. [S.l.]: NASA Headquarters, 2001.

Super-Gaussian random vibration fatigue accelerated testing model

JIANG Yu, TAO Junyong, CHEN Xun

(Science and Technology on Integrated Logistics Support Technology, College of Mechatronic Engineering&Automation, National University of Defense Technology, Changsha 410073, China)

Here, a new mathematical model of accelerated vibration fatigue testing was established under super-Gaussian random vibration excitation using theoretical analysis, and detailed solving methods were presented for unknown parameters in the model. The model was verified with the actual tests. It was shown that the model can be effectively used for the practical quantitative design of accelerated vibration fatigue tests, it can be applied to assess the fatigue life and reliability of engineering structures under random vibration environment.

super-Gaussian; random vibration; vibration fatigue; accelerated model

国家自然科学基金项目(50905181)

2016-01-08 修改稿收到日期：2016-07-08

蒋瑜 男，博士，副教授，1977年生

O324

A

10.13465/j.cnki.jvs.2017.09.038