地铁致地表振动局部放大现象实测与机理分析

宗 刚， 张永红， 任晓崧

(1. 同济大学 土木工程学院结构工程与防灾研究所， 上海 200092； 2. 同济大学 土木工程防灾国家重点实验室， 上海 200092)

地铁致地表振动局部放大现象实测与机理分析

宗 刚1，2， 张永红1， 任晓崧1

(1. 同济大学 土木工程学院结构工程与防灾研究所， 上海 200092； 2. 同济大学 土木工程防灾国家重点实验室， 上海 200092)

地铁运行引发的地表竖向振动并非单调递减，存在局部放大现象。对上海3处典型的埋置地铁行经场地进行了地表振动实测，实测结果表明，各场地地表振动的衰减曲线均存在局部放大区，第一局部放大区(主放大区)最为显著，位于1倍埋深的振中距(地表与振源投影点距离)附近。基于弹性波场理论，辅以有限元数值模拟，分析主放大区的主要影响因素有：① 近场体波在地表入射与反射的叠加效应；② 入射波在场地内的行程差导致的衰减率不同；③ 地铁运行引发的场地弹性波场不均匀分布特征。因素①和因素②主要作用于剪切波分量以影响主放大区的出现位置，因素③对纵波和剪切波均有较大影响，入射波场的剪切波分量较纵波分量越占优，主放大区现象就越显著。

地铁；场地振动；振动衰减；局部放大

地铁给现代城市生活带来便利的同时，其在居住区和生产区周边运行所引发的场地振动和二次噪声问题亦随着城市化进程的不断发展而日益加剧。研究地铁运行引发场地振动的传播与分布规律，是环境振动评价和减隔振设计的理论基础。基于弹性波理论，理想半空间自由表面作用的动力荷载引发的地表响应随振中距(本文借鉴地震工程学中的相关概念，定义振源在地表的垂直投影为“振中”，地表任意一点与振中的距离为“振中距”，地下振源作用点至地表的垂直距离为“埋深”，下文同)增加而单调衰减，且总体衰减率依振中距的负指数规律分布[1-3]。实际场地及振源等均非理想情况，导致地表实际振动衰减规律与理想曲线存在差异。以往对地铁或其他轨道交通引发场地振动问题的研究结果亦表明，随振中距的增加，在衰减曲线的某些区段存在振动反弹放大现象[4-7]，当地铁作为埋置振源时，地表衰减曲线的振动反弹现象更加显著[8-11]。这一问题虽被注意到，但大部分对埋置地铁引发的地表振动响应预测模型中均忽略其影响，而对该问题的机理分析更少。除马蒙等基于试验及弹性波动理论对埋置地铁引发的均匀半空间地表振动局部放大问题进行了较为深入的探讨外，其余的研究成果大多仅在概念层面进行了定性解释。

对于埋置地铁引发的场地振动问题，振动衰减的局部放大效应显著，尤其是距振中最近的第一反弹放大区(下文简称“主放大区”)，其振动水平往往接近甚至超过振中点的响应，振动评价及振动预测时不容忽视，有必要对这一问题的物理机制进行深入分析。基于此，本文首先对上海市3处典型的地铁行经场地进行了地表振动响应实测，振动衰减规律验证了主放大区的存在；其后，基于弹性波场理论，深入探讨了地表振动衰减曲线主放大区的形成机理。

1 振动实测

1.1 实测概况

振动实测场地为上海市某地铁线路行经的3处沿线区域，分别命名为场地一、场地二和场地三，场地主要概况见表1和图1。测线垂直于地铁轨线，测点数量及位置依场地条件确定，表1中的隧道埋深指地表至轨顶距离。振动采集设备采用Kinemetrics®公司出品的Rock-Basalt-4X系列振动信号采集仪，拾振器为Episensor32型三轴力平衡式加速度计，采样率500 sps，传感器灵敏度大于10 000 mV/g(g为重力加速度)。现场同时采集水平正交及铅垂向3个方向的加速度响应，考虑到环境振动评价多以铅垂向响应为指标，本文仅对实测的铅垂向分量进行分析。

表1 场地一～场地三概况

(a) 场地一

(b) 场地二

(c) 场地三

1.2 振动衰减规律

综合分析实测样本可知，样本的持时长度与车速相关，其近似为列车长度与车速比值，总时长在10～15 s，各场地地表响应的主频带基本介于40～80 Hz。图2给出了场地二某典型测试样本的时程曲线及其Fourier谱。

每一测点获取类似图2的有效样本数量不少于30个，依照式(1)和式(2)计算各测点的归一化响应统计量，可得各测线的振动衰减曲线如图3所示，图3中的离散点位即为各测线上的测点位置。

(1)

(2)

式中:Arsm,i为第i个测点响应的统计量;Arsm,r为归一化响应统计量(各测线选取各自参考点);Anor,i为第i个测点的规一化值；aj为第k个样本在j时刻的加速度响应值;n为某一样本的总点数；对于某给定测点，其有效样本数共m个。

(a)

(b)

由图3可见，三个场地的振动衰减规律虽有所差异，但共性明显：随振中距的增加，振动水平总体衰减，但在某些区域出现了局部放大，其中主放大区的局部放大效应最显著(放大率达到2倍以上)，主放大区均出现在振中距为(1～1.5)倍埋深区域。

图3 场地一～场地三地表振动实测衰减曲线

实测衰减曲线验证了地表振动衰减曲线存在主放大区，虽然三处实测场地的土层组成、轨线埋深、列车车速及地表响应频谱等因素均不同，但主放大区的出现位置及反弹量等指标有共性，说明振动主放大区的形成存在其固有的物理机制，研究其形成机理具有理论可行性。

2 振动主放大区形成机理分析

马蒙等对振动局部放大区的解释是地表面波与体波形成的能量叠加效应，夏禾等认为地表振动局部放大区是弹性波在基底反射后与直达波形成的能量聚焦区，文献[12]对主放大区的解释则考虑了地铁隧道空腔对弹性波传播的阻障作用。上述这些观点，可以从某些侧面解释主放大区的形成机理，但缺少系统和定量分析。本文基于弹性波射线理论及有限元数值模拟方法，忽略场地实际参数绝对量值的影响，选取一系列无量纲量参数(体波反射系数、体波衰减修正系数、隧道与土体波阻抗比、波场分布相对系数、振中距与隧道埋深比等)，从问题固有的物理机制角度分析主放大区的形成机理。

2.1 体波分量的叠加效应

对于埋置振源产生的振动问题，振中距在2～5倍埋深范围内时，地表振动响应主要由体波控制[13-14]。地表振动响应表现为入射波分量与反射波分量在同一空间点的瞬时叠加效应，纵波(P波)和剪切波(SV波)的不同反射规律及因入射行程差引发的不同衰减率等因素，均影响地表振动响应的最终叠加结果。

二维均质半空间内的平面体波(P波和SV波)以任意角度入射至自由界面时将发生反射及模式转换，在给定材料泊松比条件下，自由界面处各体波分量的位移反射系数仅与入射角有关。当埋深一定时，自由界面上各振动接收点处入射波行程(r)随入射角的增大而增加， P波振幅随r的增加依r-2衰减，SV波的衰减率为r-1，不同衰减率导致各入射点处的入射波振幅不同，其示意如图4所示。基于此，可得自由界面处考虑体波衰减效应后平面波的反射系数如式(3)和式(4)所示。

(3)

(4)

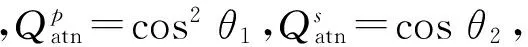
(5)

图4 入射波振幅在自由界面处的衰减

自由界面上任一点的竖向振动可通过位移矢量竖向分量叠加得到，见式(6)和式(7)。其中入射P波在自由界面处不存在全入射问题，但SV波应考虑一般反射和全反射两种情况。

(6)

(7)

式中,θcrt=arcsin(Csp)为SV波入射至自由界面时的临界角，β1和β2分别为与入射纵波和入射剪切波对应的SV波反射角。

对应不同的介质泊松比，依式(6)和式(7)绘制出自由界面上竖向振动位移幅值与振中距的关系曲线，如图5所示。图中曲线表明，随振中距的增加， P波分量对应的衰减曲线单调递减，振中距<1.5倍埋深时，衰减速率较快，其后衰减速率减缓；SV波分量对应的衰减曲线非单调递减，振中距<1倍埋深时衰减系数递增，振中距为1倍埋深时，系数达到极大值，其后再逐渐减小，即对应SV波入射，地表竖向振动响应在振中距为1倍埋深时出现极值。此外，泊松比仅影响SV波分量对应衰减曲线在临界入射角以前的区域。

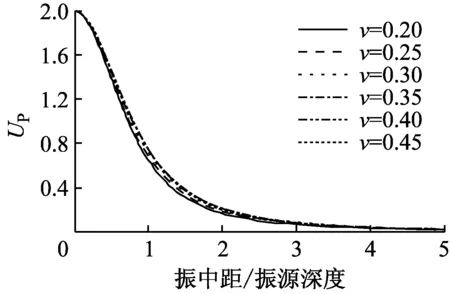
(a) P波入射

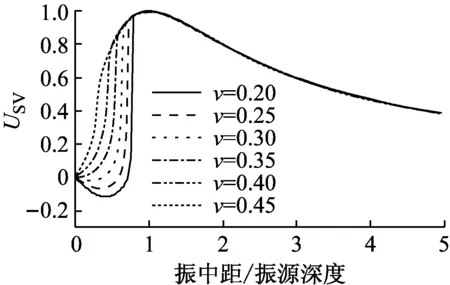
(b) SV波入射

假定入射至界面的P波和SV波分量相等，图6给出了P波和SV波综合作用下的地表振动衰减曲线。可见，泊松比不大于0.35时，振动衰减曲线在振中距接近1倍振源埋深时存在明显的局部放大现象，即出现了主放大区，这与实测的振动衰减曲线类似；当泊松比达到0.4并继续增大后，地表响应最大值出现在振中距接近0.5倍埋深的区域范围内，衰减曲线的主放大区退化为曲线的第一振动极值区。

图6 地表振动衰减曲线

显然，自由界面处体波的入射与反射分量叠加、体波随入射角变化具有不同衰减率等因素是形成主放大区的重要原因，其中SV波分量对地表衰减曲线主放大区的影响较大。换言之，应力波场以SV波分量为主导时，地表衰减曲线的主放大区将更显著，反之，衰减曲线将趋近于单调递减趋势。

2.2 非均匀波场的影响

实际的“地铁隧道—土体”场地中，竖向激励作用下产生的振动经隧道向土体内传播时产生的弹性波场非均匀分布，有必要分析波场非均匀分布对主放大区的影响。在该种情况下，合理的有限元数值解能较好的解决经典弹性波理论无法获得显式解析表达的问题[15-18]。列车行经某一测试断面时引发的地表竖向振动响应能量主要受与该断面最临近一节车厢的影响[19]，就整列车而言，某一断面的振动响应可近似为平面应变问题。基于此，本文考虑二维平面应变有限元动力分析问题。

有限元模型中，埋深起始点近似取为隧道底部，隧道半径与埋深比取0.133，隧道与土体材料的波阻抗(剪切波速与材料质量密度的乘积)比取10.0，材料泊松比取0.25，单位波长与单元尺寸的比值取20，满足单元尺寸对波长的要求。荷载采用类脉冲的高斯调制函数形式，见式(8)，不考虑材料的阻尼效应。

(8)

式中:t为时间参数;t0为选取的高斯函数中心;σ0控制脉冲激励的作用时长。本文有限元计算的时间步长取0.000 5 s，对应脉冲荷载作用时间增量步数>200，可以消除波前以后的振荡影响。

在式(8)的竖向冲击力作用下，场地内的波场以隧道周边土体应力集中区为次生振源向外传播一定距离后，形成稳定波场，波场快照见图7。可见，合理地选择时间步长增量及单元尺寸后，有限元数值解对弹性波场的近似效果良好。

图8分别给出了距隧道壁0.3倍埋深的圆周面上的相对应力幅值系数(Rr，对应Mises等效应力有效值)分布图。需说明的是，此时将土体内的应力波场近似为与隧道同心的圆周分布，当隧道半径与埋深比值<0.25时，这一近似处理产生的误差较小。显然，应力幅值沿圆周非均匀分布，0°～40°夹角区间内P波分量占主导，40°～90°夹角区间内SV波分量占主导。

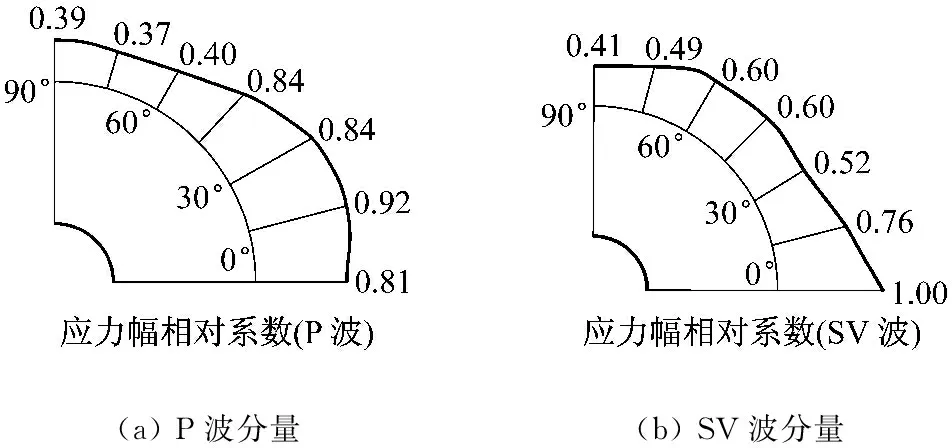
(a)P波分量(b)SV波分量

图8 应力波相对幅值系数

Fig.8 Ralative coefficient of wave amplititue

计及不均匀分布系数(Rr)的影响，仍以振中点入射波振幅作为归一化参考值，此时在考虑体波行程衰减效应时尚应计及隧道半径的影响，式(3)和式(4)中的体波衰减系数修正为式(9)的形式。该式综合考虑了波场不均匀分布及体波衰减效应的影响，其与任一振源距离处的波场分布相对系数、隧道半径与埋深的比值及入射角等参数有关。

(9)

经式(9)修正后的地表振动衰减曲线由图9给出。显然，由于应力波场的不均匀分布及体波衰减效应的影响，地表竖向振动响应衰减曲线在振中距接近1倍埋深时存在明显的主放大区，相比于等振幅入射波场而言，主放大区分布更加宽泛，反弹效应更为显著。对比图3与图9可知，在考虑波场不均匀分布影响后，地表衰减曲线的理论分析结果与实测曲线的整体趋势吻合较好。

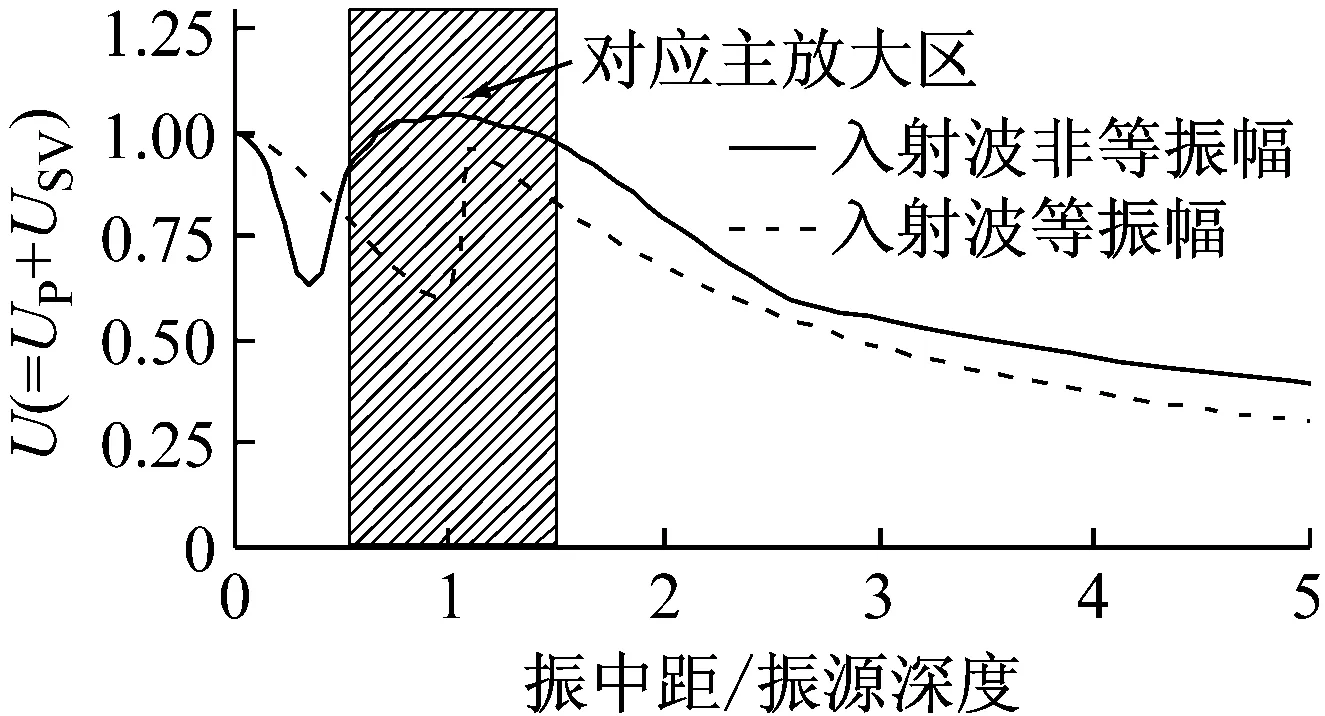
图9 考虑波场不均匀分布前后的振动衰减曲线(材料泊松比=0.25)

Fig.9 Attenuation curves of surface vibration with and without consideration of non-uniform wave field (poisson ratio=0.25)

2.3 主放大区形成机理

综合2.1节、2.2节的分析结果，地表振动衰减曲线主放大区的形成机理可总结为以下几方面。

(1) 体波在自由界面入射、反射分量的叠加效应及入射角对竖向分量叠加结果的影响。体波在自由界面发生反射后，因反射系数及模式转换系数的不同，使各分量产生了不同的综合叠加结果，特别地，对于剪切波(SV波)而言，其贡献的地表竖向分量对振动衰减曲线的分布形态影响较大，在SV波以临界角入射后，地表衰减曲线不再下降，甚至出现上升段。

(2) 体波幅值在场地内随传播距离增加而发生的几何衰减效应。这一效应导致地表各点入射波振幅随振中距的增加而迅速减小，相应地，SV波分量对应的衰减曲线在大于临界角入射后的区域将呈现局部放大现象，即出现了主放大区。

(3) 竖向动力荷载作用下含隧道土体内弹性波场不均匀分布的影响。实际含有隧道的场地在竖向动力荷载作用下，应力波场中的SV波和P波分量占比不同，同一分量在同相波阵面上的振幅分布亦不同，这都将影响衰减曲线的分布趋势。而当SV波分量在波场中占优时，地表振动衰减曲线的主放大区将更为突出。实际工程中，隧道与土体的波阻抗比一般为10左右，此时由隧道内竖向动力荷载作用引发的土体应力波场中SV分量大多占优，相应的地表衰减曲线主放大区均较为显著。

(4) 其他主要影响参数。土的层状分布、隧道结构形式、动力激励特征及材料阻尼等参数均对主放大区均有影响。因层状土间发生透射后的出射角变化、SV波全反射及折射波等因素将影响主放大区的出现位置及放大程度；隧道结构和激励特性将影响场地内波场的分布特征，进一步影响主放大区；阻尼的影响主要体现在对体波随行程增加而发生的衰减特性方面，进而影响主放大区的分布。关于这些参数的深入分析，将另有研究成果发表，本文不再展开。

3 结 论

本文首先完成了地铁运行引发的场地振动实测与数据分析，实测结果验证了地表振动衰减曲线存在主放大区，主放大区基本出现在振中距接近(1～1.5倍)埋深的范围内。基于弹性波场射线理论，辅以有限元数值模拟，分析主放大区的形成机理是：近场体波在地表的入射与反射叠加效应及体波的衰减效应，导致地表振动衰减曲线出现主放大区，泊松比会影响主放大区的出现位置和反弹程度；作用于隧道内的竖向动力荷载形成的场地波场非均匀分布特征对主放大区有重要影响，综合而言，场地内剪切波分量较纵波越占优，地表振动衰减曲线的主放大区现象就越显著。土的层状组成、隧道结构、激励频率及材料阻尼等亦对主放大区有不同程度影响，有待进一步研究。

[1] LAMB H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society A, 1904, 203(359-371): 1-42.

[2] GRAFF K F. Motion in elastic solids[M]. Oxford: Clarendon Press, 1991.

[3] 王贻荪. 地面波动分析若干问题[J]. 建筑结构学报, 1982(2): 56-67.

WANG Yisun. Some problems in the ground vibration analysis[J]. Journal of Building Structures, 1982(2): 56-67.

[4] 贾宝印，楼梦麟，宗刚,等. 车辆荷载引起地面振动实测研究[J]. 振动与冲击,2013, 32(4):11-14.

JIA Baoyin, LOU Menglin, ZONG Gang, et al. Field measurements for ground vibration induced by vehicle[J]. Journal of Vibration and Shock, 2013, 32(4): 11-14.

[5] 夏禾, 曹艳梅. 轨道交通引起的环境振动问题[J]. 铁道科学与工程学报, 2004, 1(1): 44-50.

XIA He, CAO Yanmei. Problem of raliway traffic induced vibrations of environments[J]. Journal of Railway Science and Engineering, 2004, 1(1): 44-50.

[6] 郑鑫, 陶夏新, 王福彤, 等. 轨道交通地面振动衰减关系中局部放大现象形成机理研究[J]. 振动与冲击, 2014, 33(3): 35-40.

ZHENG Xin, TAO Xiaxin, WANG Futong, et al. Mechanical of local amplification in attenuation of ground vibration induced by rail traffic[J]. Journal of Vibration and Shock, 2014, 33(3): 35-40.

[7] 常乐, 闫维明, 任珉, 等. 高架路交通诱发的地面振动测试与分析[J]. 振动、测试与诊断, 2009, 29(2): 175-178.

CHANG Le, YAN Weiming, REN Min, et al. Test and analysis of ground vibration induced by elevated road traffic[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(2): 175-178.

[8] 马蒙, 刘维宁, 王文斌. 轨道交通地表振动局部放大现象成因分析[J]. 工程力学, 2013, 30(4): 275-280.

MA Meng, LIU Weining,WANG Wenbin. Analysis on the reasons of ground vibration amplification induced by railway traffic[J]. Engineering Mechanics, 2013, 30(4): 275-280.

[9] 张啟乐, 刘林牙, 李纪阳. 地铁运行引起地面局部振动放大现象的数值模拟[J]. 噪声与振动控制, 2015, 35(4): 116-120.

ZHANG Qile, LIU Linya, LI Jiyang. Numerical analysis of ground vibration amplification phenomenon caused by subway operation[J]. Noise and Vibration Control, 2015, 35(4): 116-120.

[10] 单涛涛, 楼梦麟, 蒋通, 等. 地铁诱发地面振动传播衰减特性分析[J]. 防灾减灾工程学报, 2013, 33(4): 461-467.

SHAN Taotao, LOU Menglin, JIANG Tong, et al. Analysis on propagation attenuation of subway-induced ground vibrations[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(4): 461-467.

[11] 闫维明, 张祎, 任珉,等. 地铁运营诱发振动实测及传播规律[J]. 北京工业大学学报, 2006, 32(2): 149-154.

YAN Weiming, ZHANG Yi, REN Min, et al. In situ experimental and analysis of environmental vibration induced by ruban subway transit[J]. Journal of Beijing University of Technology, 2006, 32(2): 149-154.

[12] THOMPSON D. Railway noise and vibration: mechanisms, modelling and means of control[M]. Elsevier Science & Technology, 2008,153(4):21-25.

[13] PEKERIS C L. The seismic buried pulse[J].Proceedings of the National Academy of Sciences, 1955, 41(9): 629-639.

[14] KUZNETSOV S V, TERENT’EAV E O. Wave fields and domination regions for the Interior Lamb Problem[J]. Mechanics of Solids, 2015, 50(5):508-520.

[15] 刘晶波, 廖振鹏. 离散网格中的弹性波动(II)[J]. 地震工程与工程振动, 1989, 9(2): 1-11.

LIU Jingbo, LIAO Zhenpeng. Elastic wave motion in discrete grids (II)[J]. Earthquake Engineering and Engineering Vibration, 1989, 9(2): 1-11.

[16] KOUROUSSIS G, VANPARYS L, CONTI C, et al. Using three-dimensional finite element analysis in time domain to model railway-induced ground vibrations[J]. Advances in Engineering Software, 2014, 70(2): 63-76.

[17] KOUROUSSIS G, CONNOLLY D P, OLIVIER B, et al. Railway cuttings and embankments: experimental and numerical studies of ground vibration[J]. Science of the Total Environment, 2016, 557-558: 110-122.

[18] 廖振鹏. 近场波动问题的有限元解法[J]. 地震工程与工程振动, 1984, 4(2): 1-14.

LIAO Zhenpeng. A finite element method for near-field wave motion in heterogeneous materials[J]. Earthquake Engineering and Engineering Vibration, 1984, 4(2): 1-14.

[19] 吕鹏, 宗刚，李文涛, 等. 地铁引发场地振动的实测信号能量分析[J]. 工程力学, 2013, 30(增刊1): 325-328.

LÜ Peng, ZONG Gang, LI Wentao, et al. Energy analysis of ground vibration induced by subway trains[J]. Engineering Mechanics, 2013, 30(Sup1): 325-328.

In-situ measurement and mechanism analysis for Local amplification phenomena of metro induced ground-borne vibration

ZONG Gang1,2, ZHANG Yonghong1, REN Xiaosong1

(1. Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

The surface vertical vibrations induced by metro do not decay monotonously. There is a region called the local amplification region (LAR) with an offset to the epicenter. In-situ vibration measurements were conducted at three representative sites passed by buried metros. The results showed that there are LARs for each vibration attenuation curve of 3 sites; the first LAR defined as the major amplification region (MAR) is the most siginificant and appears with a distance of about one burial depth from the epicenter; base on the theory of elastic wave propagation and numerical simulation of finite element, the major influence factors on the MAR are ① the superposition effect of incident and reflected waves within the near filed region ② the different attenuation rates of incidents due to different traveing distances ③ the non-uniform wave field distribution characteristics induced by metro; the factor ① and ② act on shear wave components to affect the position of the MAR; the factor ③ acts on both shear and longitudinal waves; the more the shear wave components than the longitudinal ones，the more remarkable the MAR phenomenon.

metro; ground-borne vibration; vibration attenuation; local amplification

上海市自然科学基金基础(13ZR1444800)

2016-01-08 修改稿收到日期：2016-05-26

宗刚 男，博士，讲师，1977年生

任晓崧 男，博士，高级工程师，1968年生

U231

A

10.13465/j.cnki.jvs.2017.09.036