Y形高强钢组合偏心支撑框架结构抗震性能简化分析方法研究
2017-05-17苏明周
连 鸣, 苏明周, 郭 艳
(1. 西安建筑科技大学 土木工程学院, 西安 710055; 2. 西安建筑科技大学 材料科学与工程博士后流动站, 西安 710055)
Y形高强钢组合偏心支撑框架结构抗震性能简化分析方法研究
连 鸣1,2, 苏明周1, 郭 艳1
(1. 西安建筑科技大学 土木工程学院, 西安 710055; 2. 西安建筑科技大学 材料科学与工程博士后流动站, 西安 710055)
通过对1∶2缩尺三层Y形高强钢组合偏心支撑框架结构(Y-HSS-EBF)模型试件的振动台试验,考察了结构的抗震性能。基于结构的恢复力模型与等代拉杆简化模型,采用SAP2000程序中的多线段塑性Kinematic连接单元代替拉杆,进行Y-HSS-EBF结构的地震反应简化分析,并将简化分析计算结果与试验结果、有限元计算结果进行了对比。研究结果表明:Y-HSS-EBF结构具有良好的抗震性能;由简化计算方法得到的Y-HSS-EBF结构滞回曲线与试验结果基本一致,简化分析模型能较好地模拟结构的非线性性能;振动台模型的简化计算结果具有一定的精度,简化分析模型能够较好的用于Y-HSS-EBF结构的弹性与弹塑性地震反应分析。在初步设计时,可采用简化分析模型对结构地震作用进行计算。
偏心支撑; 高强钢; 恢复力模型; 地震反应; 简化分析
偏心支撑框架结构结合了中心支撑框架结构的刚度和框架结构的延性,结构利用耗能梁段的塑性变形耗散地震能量。国内外学者的研究结果表明,偏心支撑框架结构是一种良好抗震结构体系[1-5]。偏心支撑框架结构在设计时可根据结构的高度、跨度和结构布置选择合适的耗能梁段和偏心支撑类型。相对于常见的K形、D形、V形偏心支撑结构,Y形偏心支撑结构的耗能梁段置于框架梁外,耗能梁段的塑性变形主要为水平方向剪切屈服变形,不会对横梁及楼板造成严重损坏,耗能梁段震后更易修复。
高强钢组合偏心支撑框架结构的耗能梁段采用屈服点较低且延性较好的钢材(如Q235钢、Q345钢),框架梁、柱采用高强钢(如Q460钢、Q690钢),结构在大震作用下,耗能梁段能够充分发展塑性进行耗能,框架梁、柱由于采用高强钢,仍处于弹性或部分进入塑性,从而达到抗震设防目标。已有的试验和数值分析研究结果表明,高强钢组合偏心支撑框架结构是一种良好的抗震结构体系[6-10]。
虽然国内外学者已对偏心支撑框架结构进行了大量的理论和试验研究,但对结构地震反应的简化分析方法研究较少。本文在Y形高强钢组合偏心支撑框架结构(Y-HSS-EBF)振动台试验的基础上,利用该结构的恢复力模型与等代拉杆简化模型,利用SAP2000程序中的多线段塑性Kinematic连接单元代替拉杆,进行Y-HSS-EBF结构的地震反应简化分析,并将简化分析计算结果与试验结果、有限元计算结果进行了对比以验证方法的合理性,为Y-HSS-EBF结构初步设计时的地震作用计算提供参考。
1 振动台试验
1.1 试验试件
试验模型试件为1∶2缩尺的三层Y-HSS-EBF结构,设计条件:抗震设防烈度为8度,设计地震基本加速度为0.2g,设计地震分组为第二组,Ⅱ类场地。输入地震波加速度相似比采用1.2∶1,基于加速度相似比计算得到的模型试件主要物理相似关系见表1。

表1 模型主要物理量相似比
模型试件设计参考偏心支撑框架结构基于性能的塑性设计方法[11-13]及我国《高层民用建筑钢结构技术规程》(JGJ 99-98)[14]、《建筑抗震设计规范》(GB 50011—2010)[15]。模型试件跨度为2.825 m,层高为1.8 m,结构布置见图1。采用C30现浇混凝土楼板,厚度为80 mm,配筋采用B6钢筋双层双向布置,在框架梁上翼缘中心处沿梁的长度方向每隔100 mm布置栓钉以保证楼板与框架梁连接可靠。耗能梁段采用Q235钢,支撑采用Q345钢,框架梁、柱采用Q460钢,钢材力学性能见表2。耗能梁段长350 mm,均设计成剪切屈服型,各构件之间均采用焊接连接,模型试件的框架梁、柱、支撑、耗能梁段截面尺寸见表3。
根据我国《建筑结构荷载规范》(GB 50009—2012)[16],模型试件楼面恒载(含楼板自重)和活载分别取5 kN/m2和2.0 kN/m2,屋面恒载(含屋面板自重)和屋面雪荷载分别取5.625 kN/m2和0.325 kN/m2,墙体线荷载为4.38 kN/m。根据抗震规范荷载组合值系数及质量相似关系,模型试件楼面和屋面配重分别为5.96 kN/m2和4.85 kN/m2。

(a)平面图(b)立面图

(c) 试验试件
表2 钢材性能参数
Tab.2 Mechanical properties of steel

钢材厚度t/mm屈服强度fy/MPa极限强度fu/MPa弹性模量E×105/MPa伸长率/%Q2353283.1397.12.1431.57Q2354271.9402.12.1731.83Q2358276.7421.12.1832.18Q3456414.7542.032.1128.29Q34510363.8545.82.0128.74Q4608473.5635.12.1225.36Q46010516.0691.972.0623.51
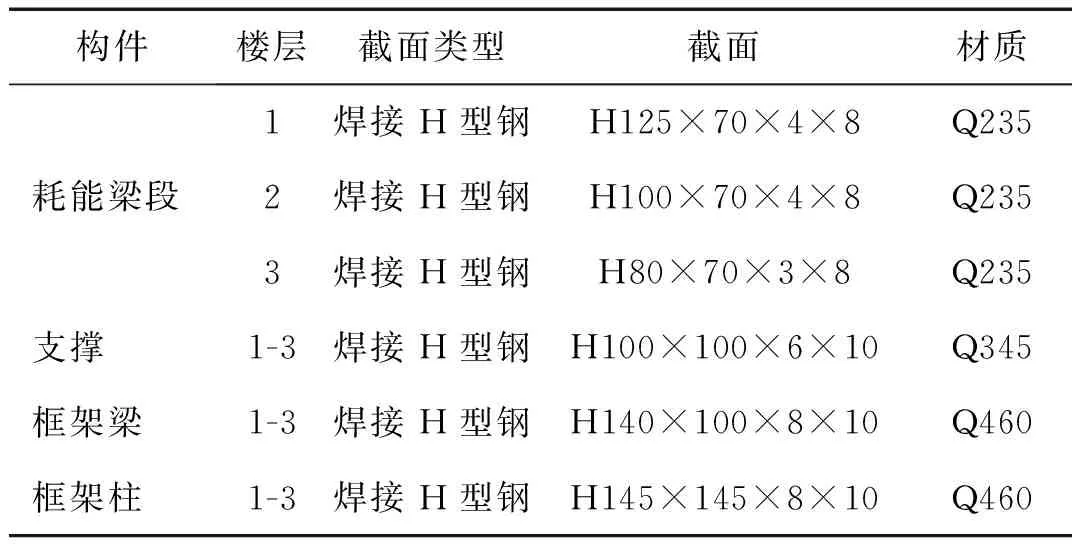
表3 构件截面尺寸
1.2 传感器布置
在模型试件底座顶面、各层楼面及屋面各布置4个加速度传感器和2个位移传感器。在耗能梁段、支撑、框架梁端、柱脚处布置应变片,如图2所示。

(a)一层耗能梁段(b)二层耗能梁段(c)三层耗能梁段

(d) 框架梁、柱脚、支撑
图2 应变布置
Fig.2 Layout of strain gauges in test model
1.3 加载工况
试验选取El Centro波、Taft波和兰州波为台面输入地震波,根据时间相似关系缩尺后的地震波见图3。试验为水平单向加载(试件轴方向,见图1),台面地震波输入加速度相似比为1.2∶1,试验工况见表4。

(a)El-Centro波(b)Taft波

(c) 兰州波
1.4 试验结果
1.4.1 试验现象
模型试件在不同工况下的主要试验现象见表5。由表5可知,在罕遇地震下,模型发生耗能梁段破坏,除耗能梁段外,其余构件未出现明显的不可恢复变形。

表4 试验加载工况
1.4.2 动力特性
试件白噪声的扫频结果见表6,由表6可知, 模型试件的自振频率和阻尼比分别为5.48 Hz和2.99%,随着台面输入地震作用的不断增大, 模型试件的阻尼比逐渐变大,自振频率逐渐下降,说明模型试件的刚度随着输入地震激励的增大而逐渐减小。
由文献[9]中刚度退化率计算公式得到的模型试件刚度变化曲线如图5所示。由图6可知:前五次白噪声结果计算得到的刚度退化率变化很小,说明模型试件在多遇地震作下的刚度与初始刚度相差不大,结构处于弹性;模型试件在8度罕遇、9度罕遇和高于9度罕遇地震作用下,刚度出现大幅度退化,最大退化幅度为37.5%;模型试件出现明显的刚度退化但未发生倒塌,表明其在大震作用后仍具有可靠的整体刚度。

表5 试验现象
1.4.3 加速度反应
图6为模型试件在不同水准的El Centro波、Taft波和兰州波作用下的楼面及屋面加速度放大系数变化曲线。由图可知:同一工况下各层的加速度放大系数沿结构高度方向逐渐递增;除个别工况外,各层加速度放大系数变化趋势大致相同;除个别工况外,各层加速度放大系数曲线随台面地震激励的增大大致呈下降趋势,说明随着地震强度的增大,模型试件的刚度出现退化。

(a)耗能梁段焊缝锈皮脱落(b)支撑焊缝锈皮脱落

(c)耗能梁段残余变形(d)耗能梁段残余变形

(e)焊缝完全断裂(f)焊缝断裂
图4 试验现象
Fig.4 Phenomena of test

表6 试件自振频率和阻尼比

图5 刚度退化曲线对比
1.4.4 位移反应
表7和表8分别为在不同水准El Centro波、Taft波和兰州波作用下,模型试件楼面及屋面的最大相对位移和最大层间侧移角,表中PGA表示台面输入地震波的峰值加速度。由表可知:在多遇地震作用下,模型试件各层的最大相对位移相差较小;在8度罕遇甚至更高烈度地震作用下,模型试件各层最大相对位移变化显著,其中第一、三层最大位移的变化幅度较大;模型试件在多遇地震和罕遇地震下的最大层间侧移角分别为1/872和1/71,满足我国抗震规范GB 50011—2010相应层间侧移角限值的要求。

(a)ElCentro波(b)Taft波

(c) 兰州波
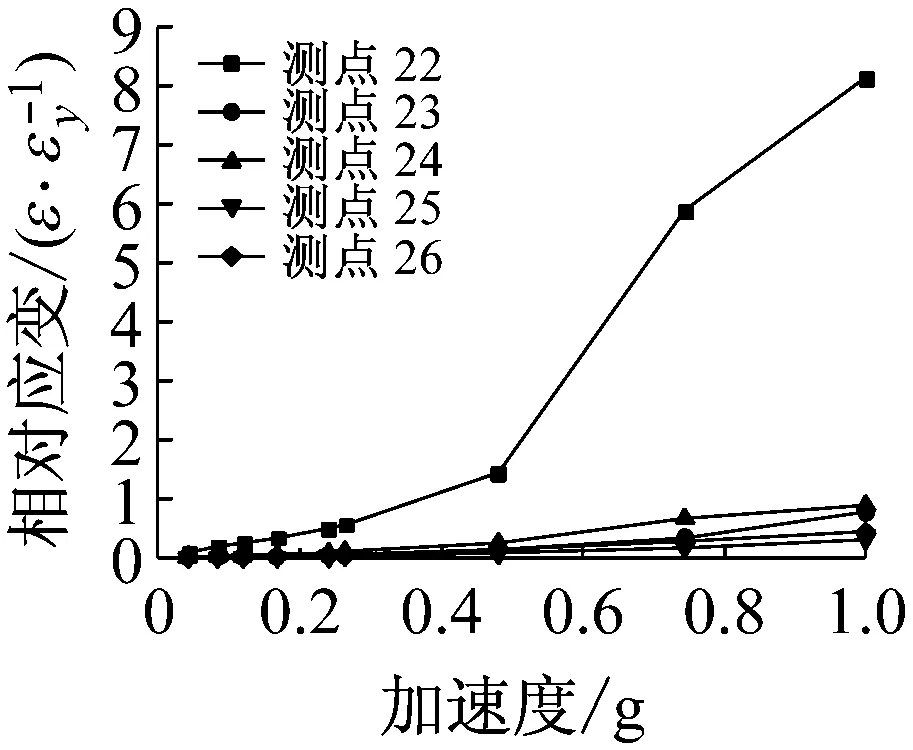
1.4.5 应变反应
图7~图9为模型试件各测点的应变变化规律,其中相对应变是指应变实测值与屈服应变的比值。由图可知:在多遇地震作用下,各测点应变值均小于屈服应变,构件处于弹性状态;在不同水准的地震波作用下,模型试件各层耗能梁段腹板应变值明显高于翼缘应变值,在8度罕遇以及更高烈度罕遇地震作用下,各层耗能梁段腹板应变值显著增大,且超过屈服应变,说明耗能梁段在罕遇地震作用下发生剪切屈服变形;在罕遇地震作用下,耗能梁段腹板进入塑性,框架梁端、支撑及柱脚的应变反应均小于屈服应变,说明模型试件在罕遇地震作用下,耗能梁段进入塑性耗散地震能量,而框架梁、柱及支撑仍处于弹性状态,符合偏心支撑结构的设计预期。
综上所述,模型试件具有良好的抗震性能,结构在地震作用下的层间变形满足规范要求,在罕遇地震作用下耗能梁段进入塑性耗散地震能量,其余构件保持弹性状态,结构无倒塌危险,能够满足“小震不坏、中震可修、大震不倒”的抗震设防准则。

表8 模型试件最大层间侧移角
2 单层单跨Y-HSS-EBF结构简化分析
2.1 方法概述
与其他形式的偏心支撑结构不同,Y形偏心支撑结构的耗能梁段在框架梁外,本文在Y-HSS-EBF结构恢复力模型[17]与等代拉杆简化模型的基础上,利用SAP2000程序中的多线段塑性Kinematic连接单元代替拉杆,进行Y-HSS-EBF结构的地震反应分析。如图10所示,将Y-HSS-EBF结构简化为相互铰接的杆系模型,框架梁和框架柱分别等效为模型的横杆和竖杆,Y形偏心支撑和耗能梁段等效为斜向Kinematic连接单元。则结构的抗剪性能取决于连接单元的轴向变形能力,两者间力与位移转化关系为
(1)
式中,P和Δ分别为单层结构的水平外力和水平位移,两者由Y-HSS-EBF结构的恢复力模型进行确定。

(a)一层(b)二层
(c) 三层

(a)一层(b)二层

(c) 三层
Y-HSS-EBF结构简化模型的抗剪性能取决于Kinematic连接单元的轴向变形能力。在相同条件下,SAP2000程序对Kinematic连接单元的计算速度明显高于各构件均采用梁单元的有限元模型,当计算非线性工况,特别是耗能梁段出现塑性变形时,会影响梁单元模型的计算速度,因此采用简化模型可减少计算耗时。另外,耗能梁段长度对结构的抗震性能影响较大[18-19]。在SAP2000程序中,建立Y-HSS-EBF结构的梁单元模型并不复杂,在初步设计时,当结构的跨度、高度及布置方案确定后,为设计合理的耗能梁段长度以确保结构具有足够的承载力和抗震性能,可能需进行多次建模分析,此过程中可能需多次重建耗能梁段和支撑部件,而采用简化模型进行分析时,只需修改Kinematic连接单元的属性即可完成重新建模,因此可提高初步设计时的建模效率。

(a)一层(b)二层

(c) 三层

图10 简化分析模型
2.2 简化分析计算结果与试验结果比较
采用上述方法,在SAP2000程序中建立文献[7]单层单跨Y-HSS-EBF结构试验试件的Kinematic连接单元简化分析模型,如图11所示。通过式(1)将试件的恢复力模型进行转化,并将转化后的力-变形关系定义到Kinematic连接单元参数中。使用SAP2000对简化分析模型进行滞回分析,需在程序中定义一系列非线性分析工况,并将各工况连接起来以模拟试验的循环加载。程序中的水平加载采用位移控制,并与文献[7]中的试验加载制度保持一致。

图11 SAP2000简化分析模型
由非线性简化分析方法得到的试件滞回曲线与试验曲线对比结果如图12所示。由图可知:计算结果与试验结果的骨架曲线比较接近,简化计算方法能较好的模拟结构的强度和刚度,由于采用双线性恢复力模型进行简化分析,使计算滞回曲线的滞回环包络面积略小于试验曲线。总体上讲,以上简化分析方法可以较好的用于Y-HSS-EBF结构的非线性分析。
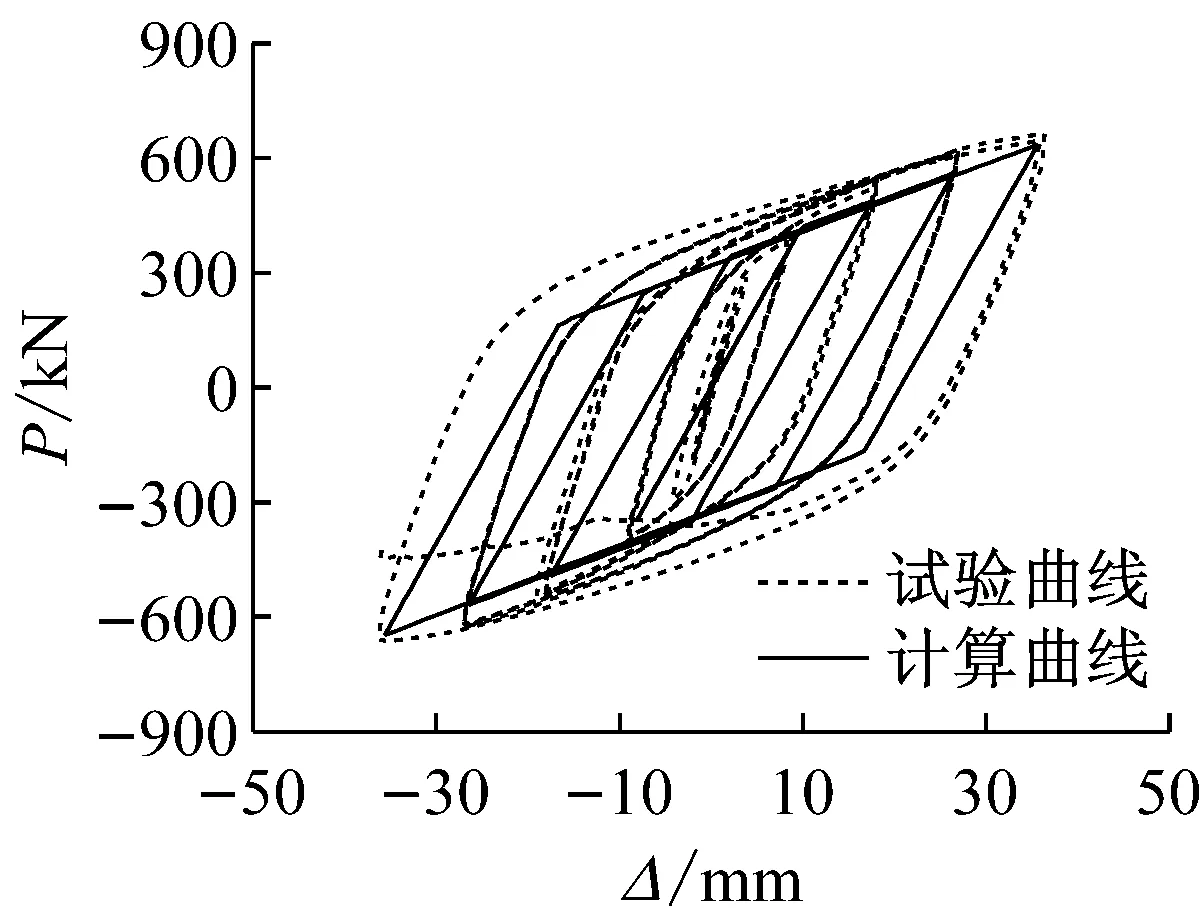
(a) 试件1

(b) 试件2
3 多层Y-HSS-EBF结构简化分析
3.1 方法概述
为考察本文提出的简化分析方法对多层Y-HSS-EBF结构弹性和弹塑性地震反应计算的适用性,根据上述单层单跨结构的简化分析方法,对本文三层Y-HSS-EBF结构振动台试验研究中的模型试件进行简化建模分析,具体做法是将试件各层的Y形偏心支撑结构按照上述方法进行简化,试验模型试件在SAP2000中的简化分析模型如图13(a)所示。同时,在SAP2000中建立试验模型试件的梁单元有限元模型(如图13(b)所示)。试验配重以面荷载的形式施加于简化模型与有限元模型的楼面板、屋面板上。对简化分析模型与有限元模型进行7度~9度多遇和罕遇水准的El Centro波、Taft波和兰州波加载,并将简化计算结果与试验结果、有限元计算结果进行对比。
3.2 简化计算结果与试验结果、有限元计算结果的比较
3.2.1 模态分析结果对比
对简化分析模型进行模态分析,由次得到的1阶频率与试验结果、有限元计算结果的比较如表9所示。

(a)简化模型(b)有限元模型
图13 振动台试验试件分析模型
Fig.13 Analysis models of shake table test specimen
由表9可知:简化模型1阶频率略高于试验值,两者相差11%;简化计算结果与有限元计算结果相差不大。

表9 模态分析频率与试验频率对比
3.2.2 加速度反应对比
简化模型在不同水准地震波下的楼层最大加速度与试验结果、有限元计算结果的比较如表10和图14所示。由图表可知:仅在个别工况下的简化模型楼层最大加速度与试验值的偏差超过20%;大部分工况下简化模型的楼层最大加速度与试验值相差在10%以内;在多遇地震下,简化模型的楼层最大加速度与试验结果、有限元结果偏差相对较小;在罕遇地震下,简化模型楼层最大加速度与试验结果的偏差随地震烈度的增加大致呈增大趋势,原因为试验模型试件在经过一系列地震波作用后刚度退化,而简化模型无法模拟结构的刚度退化,因此误差有变大的趋势。
3.2.3 位移反应对比
简化模型在不同水准地震波下的楼层最大相对位移与试验结果、有限元计算结果的比较如表11和图15所示。由图表可知:绝大部分工况下,简化模型的楼层最大相对位移与试验值相差在15%以内;由简化分析得到的楼层位移变化曲线与有限元计算曲线的变化趋势基本一致;多遇地震下,楼层最大位移简化计算结果与试验结果、有限元计算结果偏差相对较小;罕遇地震下,随着地震烈度的增加,简化计算结果与试验结果的误差大致逐渐增大,这是由于试验模型试件在经过一系列地震作用后刚度退化,而简化分析模型无法模拟结构的刚度退化,导致误差增大;简化模型在9度罕遇Taft波下的屋面最大位移与试验结果相差较大,原因在于在该水准Taft波作用下,试验模型试件三层的耗能梁段端部焊缝完全断裂导致楼层刚度变小,而简化模型无法模拟断裂,从而误差较大。

表10 简化计算最大加速度与试验结果比较

(a) 二层楼面
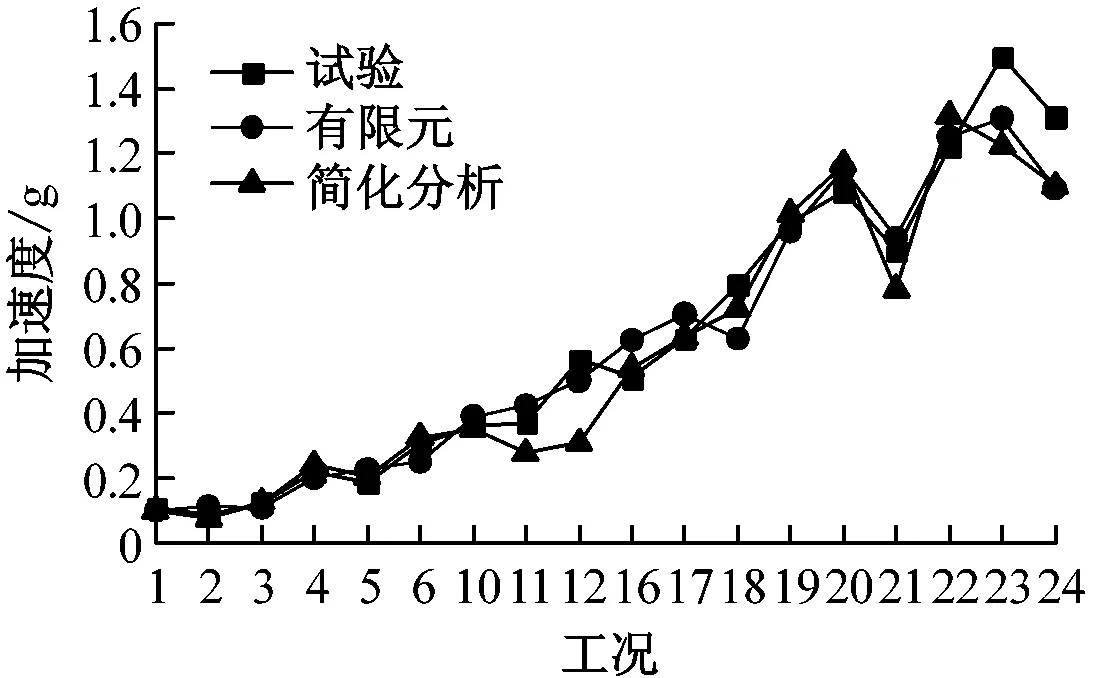
(b) 三层楼面
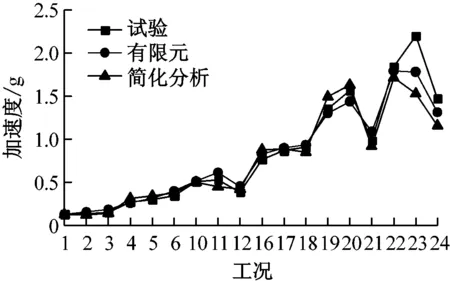
(c) 屋面
3.2.4 加速度时程曲线对比
图16~图18分别为简化模型在7度、8度和9度多遇水准El Centro波作用下的二层楼面加速度时程曲线与试验曲线、有限元计算曲线的比较。图19~图21分别为简化模型在7度、8度和9度罕遇水准El Centro波作用下的二层楼面加速度时程曲线与试验曲线、有限元计算曲线的比较。由图16~图21可知:由简化分析计算得到的楼层加速度时程曲线与试验曲线的大小和变化规律基本一致;与有限元计算曲线相比,简化计算加速度时程曲线与试验曲线更为接近;在地震波衰减阶段,简化分析模型的加速度响应略大于试验实测响应,但小于有限元模型的加速度响应。
另外,在相同的SAP2000程序运行条件下,试验模型试件的简化模型与梁单元有限元模型在计算同一工况时,前者的计算耗时可比后者减少数十倍,尤其是计算非线性工况时,简化模型可较大程度的提高计算速度,减少计算耗时。
以上分析表明,简化分析方法的计算误差总体上在可接受的范围内,计算结果具有一定的精度,并且能够提高计算效率,简化分析模型能够较好的用于Y-HSS-EBF结构的弹性和弹塑性地震反应分析,在初步设计时,可采用本文提出的简化分析方法对结构地震作用进行计算。
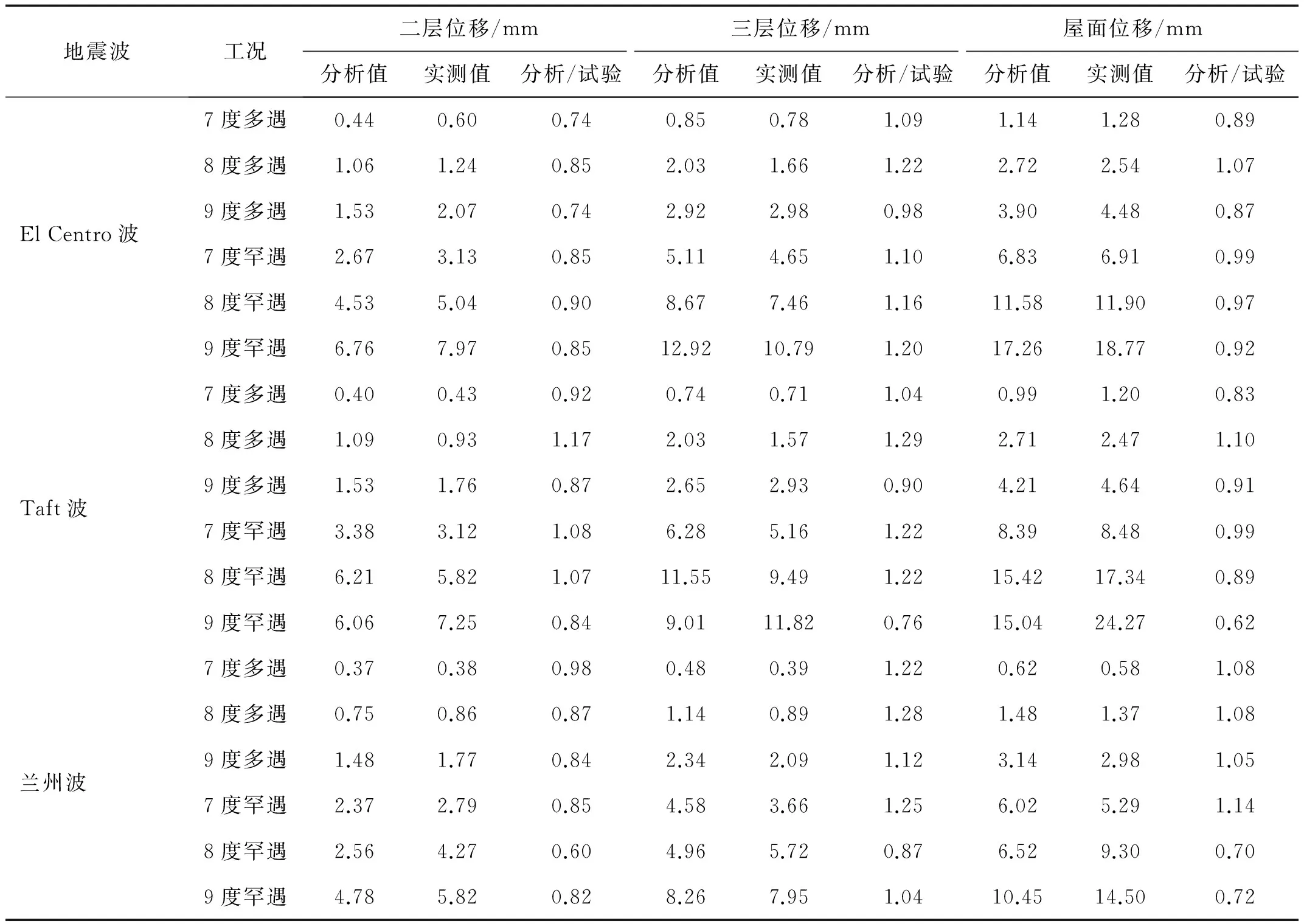
表11 简化计算最大楼层位移与试验结果比较

(a) 二层楼面

(b) 三层楼面

(c) 屋面

(a) 试验

(b) 有限元

(c) 简化分析
4 Y-HSS-EBF结构地震简化分析步骤
Y-HSS-EBF结构地震简化分析步骤具体如下:
(1) 根据单层单跨的Y-HSS-EBF结构的几何尺寸、钢材力学性能等推导结构的双线性恢复力模型,得到骨架曲线的特征点;

(a) 试验

(b) 有限元

(c) 简化分析

(a) 试验

(b) 有限元

(c) 简化分析

(a) 试验

(b) 有限元

(c) 简化分析

(a) 试验

(b) 有限元

(c) 简化分析

(a) 试验

(b) 有限元
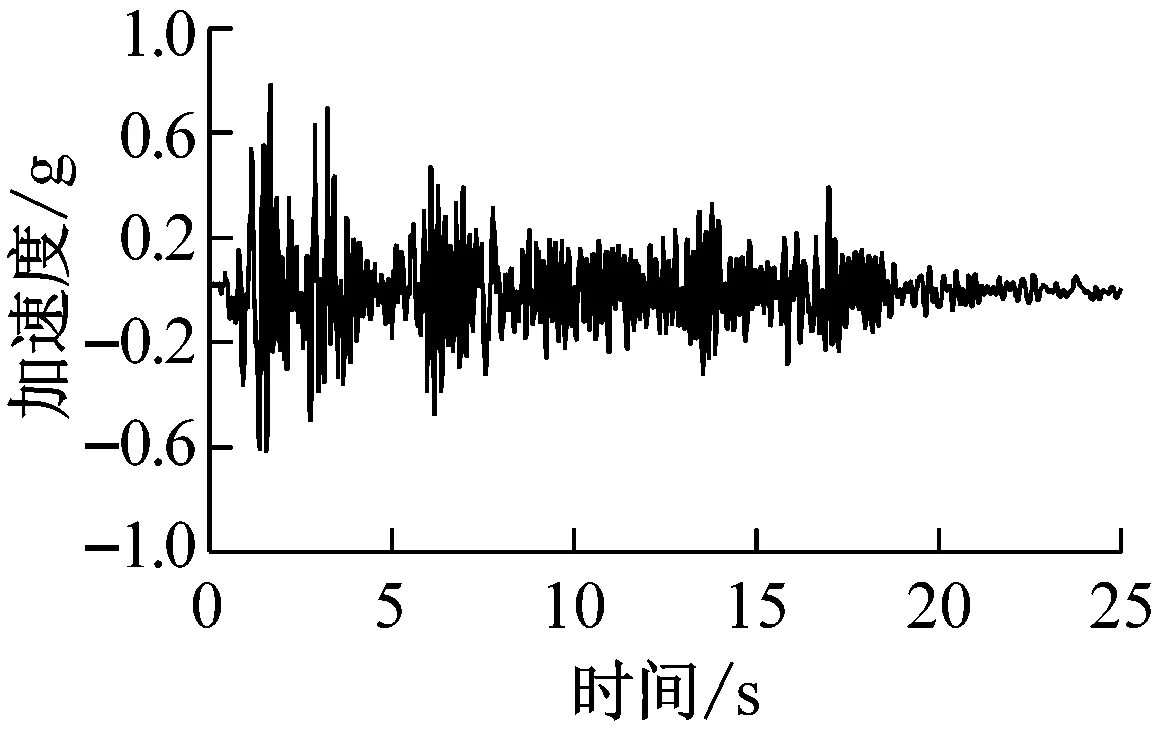
(c) 简化分析
(2) 在结构的恢复力模型的基础上,得到结构的简化分析模型;
(3) 将Y-HSS-EBF结构简化分析模型进行组装,根据结构的实际情况定义材料属性及单元类型等,建立结构的数值分析模型;
(4) 对结构数值分析模型定义并施加荷载、定义质量源、定义地震波时程曲线、定义分析工况;
(5) 对结构进行模态分析,得到其振型和频率;
(6) 在模态分析的基础上,进行结构的弹性和弹塑性地震反应分析,得到其加速度反应、位移反应和地震剪力等。
5 结 论
通过三层Y-HSS-EBF结构抗震性能振动台试验研究与Y-HSS-EBF结构地震作用简化分析方法的研究,得出如下结论:
(1) 结构在多遇地震下处于弹性状态,在罕遇地震作用下表现为耗能梁段破坏;结构在罕遇地震作用下刚度下降,但无倒塌危险;罕遇地震作用下,耗能梁段进入塑性进行耗能,其余构件处于弹性状态。结构具有良好的抗震性能。
(2) 由简化计算方法得到的单层单跨Y-HSS-EBF结构的滞回曲线与试验结果基本一致,简化分析模型能较好地模拟单层结构的非线性性能。
(3) 三层Y-HSS-EBF结构简化模型的计算结果具有一定的精度,简化分析模型能够较好的用于该结构的弹性与弹塑性地震反应分析。因此,简化分析模型适合用于工程初步设计时的结构地震作用计算。
[1] FOUTCH D A. Seismic behavior of eccentrically braced steel building[J]. Journal of Structural Engineering, 1989, 115(8): 1857-1876.
[2] PERERAL R, GMEZ S, ALARCN E. Experimental and analytical study of masonry infill reinforced concrete frames retrofitted with steel braces[J]. Journal of Structural Engineering, 2004, 130(12): 2032-2039.
[3] MAZZOLANI F M, CORTE G D, ANIELLO M D. Experimental analysis of steel dissipative bracing system for seismic upgrading[J]. Journal of Civil Engineering and Management, 2009, 15(1): 7-19.
[4] BAHRAMPOORL H, SABOURI-GHOMI S. Effect of easy-going steel concept on the behavior of diagonal eccentrically braced frames[J]. International Journal of Civil Engineering, 2010, 8(3): 242-255.
[5] 于安林, 赵宝成, 李仁达,等.K形和Y形偏心支撑钢框架滞回性能试验研究[J]. 建筑结构, 2010, 40(4): 9-12.
YU Anlin, ZHAO Baocheng, LI Renda, et al. Experimental study on hysteretic behavior ofKandY-eccentrically braced steel frames[J]. Building Structure, 2010, 40(4): 9-12.
[6] 段留省, 苏明周, 郝麒麟, 等. 高强钢组合K型偏心支撑钢框架抗震性能试验研究[J]. 建筑结构学报, 2014, 35 (7): 18-25.
DUAN Liusheng, SU Mingzhou, HAO Qilin, et al. Experimental study on seismic behavior of high strength steel compositeK-type eccentrically braced frames[J]. Journal of Building Structures, 2014, 35 (7): 18-25.
[7] 段留省, 苏明周, 焦培培, 等. 高强钢组合Y形偏心支撑钢框架抗震性能试验研究[J]. 建筑结构学报, 2014, 35(12): 89-96.
DUAN Liusheng, SU Mingzhou, JIAO Peipei, et al. Experimental study on seismic behavior of high strength steel compositeY-type eccentrically braced frames[J]. Journal of Building Structures, 2014, 35 (12): 89-96.
[8] LIAN Ming, SU Mingzhou, GUO Yan. Seismic performance of eccentrically braced frames with high strength steel combination[J]. Steel and Composite Structures, 2015, 18(6): 1517-1539.
[9] 连鸣, 苏明周, 李慎, 等.Y形偏心支撑高强钢框架结构抗震性能振动台试验研究[J]. 建筑结构学报, 2015, 36(8): 16-24.
LIAN Ming, SU Mingzhou, LI Shen, et al. Shake table test of seismic performance of high strength steel frame withY-eccentric braces[J]. Journal of Building Structures, 2015, 36(8): 16-24.
[10] 李慎, 苏明周, 连鸣, 等. 多层高强钢组合K形偏心支撑框架抗震性能研究[J]. 土木工程学报, 2015, 48(10): 38-47.
LI Shen, SU Mingzhou, LIAN Ming, et al. Seismic behavior of multi-storey high strength steel compositeK-eccentrically braced frame[J]. China Civil Engineering Journal, 2015, 48(10): 38-47.
[11] MONTUORI R, NASTRI E, PILUSO V. Theory of plastic mechanism control for eccentrically braced frames with inverted y-scheme[J]. Journal of Constructional Steel Research, 2014, 92(1):122-135.
[12] MONTUORI R, NASTRI E, PILUSO V. Rigid-plastic analysis and moment-shear interaction for hierarchy criteria of inverted Y EB-Frames[J]. Journal of Constructional Steel Research, 2014, 95(4):71-80.
[13] 李慎, 苏明周. 基于性能的偏心支撑钢框架抗震设计方法研究[J]. 工程力学, 2014, 31(10): 195-204.
LI Shen, SU Mingzhou. A performance-based seismic mothod for eccentrically braced steel frames[J]. Engineering mechanics, 2014, 31(10): 195-204.
[14] 高层民用建筑钢结构技术规程:JGJ 99-98[S]. 北京: 中国建筑工业出版社, 1998.
[15] 建筑抗震设计规范:GB50011—2010[S]. 北京: 中国建筑工业出版社, 2010.
[16] 建筑结构荷载规范:GB 50009—2012[S]. 北京: 中国建筑工业出版社,2002.
[17] 连鸣, 苏明周, 王喆.Y形高强钢组合偏心支撑框架结构恢复力模型研究[J]. 西安建筑科技大学学报(自然科学版), 2015, 47(5): 984-688.
LIAN Ming, SU Mingzhou, WANG Zhe. Restoring force model of high strength steel compositeY-eccentrically braced frame[J]. Journal of Xi’an University of Architecture & Technology (Natural Science), 2015, 47(5): 684-688.
[18] 尹倩, 苏明周, 焦培培,等. 耗能梁段长度对高强钢组合Y型偏心支撑框架受力性能影响的研究[J]. 四川建材, 2013, 39(173): 55-58.
YIN Qian, SU Mingzhou, JIAO Peipei, et al. Research on length of link beam of dual high-strength steelYstyle eccentrically braced frame[J]. Sichuan Building Materials, 2013, 39(173): 55-58.
[19] 舒伟伟, 苏明周, 连鸣. 高强钢组合Y型偏心支撑框架滞回性能影响[J]. 广西大学学报(自然科学版), 2014, 39(4): 716-723.
SHU Weiwei, SU Mingzhou, LIAN Ming. Analysis on hysteretic behavior of high strength steelY-type eccentrically braced frame[J]. Journal of Guangxi University (Natural Science), 2014, 39(4): 716-723.
A simplified analysis method for a seismic behaviors ofY-type high strength steel composite eccentrically braced frames
LIAN Ming1,2, SU Mingzhou1, GUO Yan1
(1. School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China; 2. Post-doctoral Mobile Stations of Material Science and Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)
Shaking table tests of a 1∶2 scaled three-storyY-type high strength steel composite eccentrically braced frame (Y-HSS-EBF) were conducted to study its a seismic behaviors. A simplified seismic response analysis method for Y-HSS-EBF was proposed by using the multi-linear plastic Kinematic element in SAP2000 to replace braces, based on the restoring force model of Y-HSS-EBF and the simplified model of the replacing braces. The calculated results with the simplified analysis method were compared with the test ones and those with the finite element analysis method. The results indicated that the Y-HSS-EBF has good aseismic performances; the calculated hysteresis curves of the Y-HSS-EBF agree well with the test ones and the simplified analysis model can be used for the strucfure’s performances nonlinear analysis; the simplified calculation results of the shaking table test model has a certain level accuracy, so the simplified analysis method can be used for analyzing elastic and elastoplastic seismic responses of Y-HSS-EBF; the simplified seismic response analysis method can be applied in the preliminary design of Y-HSS-EBF.
eccentrically braced frame; high strength steel; restoring force model; seismic response; simplified analysis
国家自然科学基金(51178382);“十二五”科技支撑计划项目(2013BAJ10B03-0)
2015-12-28 修改稿收到日期:2016-03-03
连鸣 男,博士,师资博士后,1987年生
苏明周 男,博士,教授,1971年生
TU391
A
10.13465/j.cnki.jvs.2017.09.032
