基于负刚度机构的高刚度-超阻尼隔振器设计与研究

董光旭， 张希农， 谢石林， 罗亚军， 张亚红

(西安交通大学 航天航空学院机械结构强度与振动国家重点实验室， 西安 710049)

第十一届全国振动理论及应用学术会议推荐论文

基于负刚度机构的高刚度-超阻尼隔振器设计与研究

董光旭， 张希农， 谢石林， 罗亚军， 张亚红

(西安交通大学 航天航空学院机械结构强度与振动国家重点实验室， 西安 710049)

为能够隔离作用在负载上的直接扰动并提高系统的阻尼特性以避免产生共振，提出一种采用磁性负刚度机构设计的超阻尼隔振系统，其由磁性负刚度机构和两对相互对压的机械弹簧并联构成；磁性负刚度机构由五块沿轴向磁化的环形永磁体构成，倾斜环形永磁体被对称地固定在基础上，运动的环形永磁体由对压的机械弹簧约束，并沿轴向发生相对运动；根据电流模型，推导了磁性负刚度机构的磁性恢复力以及磁性负刚度解析表达式；通过将隔振系统中的刚度单元和阻尼单元重新布置并引入一个内部隐性自由度，该系统被设计成与线性参考系统具有相同静刚度、相同质量以及相同阻尼的超阻尼装置；分析了该装置中刚度单元、阻尼单元以及永磁体附加质量对所设计系统阻尼、固有频率和主系统振动响应的影响。研究结果表明，所提出的隔振系统具有高刚度和超阻尼特性，能够有效抑制主系统的振动；在高频段，主系统的响应将收敛于线性参考系统。

超阻尼； 高刚度； 负刚度； 隔振

被动式隔振技术作为一种常见的低功耗、高稳定、易实现的隔振手段被广泛地应用于实际结构的抑振、减振控制当中。在高频区域，物体的振动可通过降低隔振系统的动刚度来实现有效控制，而共振区域的振动能量可通过阻尼以热能的方式耗散掉[1-2]。

阻尼是材料的三大功能特性(超塑性、阻尼特性和形状记忆特性)之一[3]。它将机械振动能量不可逆地转变成其他形式的能量。工程中常见的阻尼可分为：系统阻尼、结构阻尼和材料阻尼。其中，黏弹性材料是在工程应用中提高结构阻尼耗散的主要材料，但该类高阻尼耗散材料往往具有中/低刚度的特征，不满足实际应用中高刚度、高承载力的要求。

为了解决这个问题，一些技术人员开展了关于具有多相或具有不同分层的复合材料研究，该类材料具有高刚度和高阻尼的特性[4]。因此，设计周期结构并应用于结构的振动抑制备受学者的广泛关注，尤其是超材料的研究。这些天然或人造结构具有衰减效应，当波的频率位于他们的“盲区”，波在任何方向的传播被禁止，因而形成“带隙”[5-6]。然而，现今已存在的超材料类型对于中—低频带范围内的振动抑制效果较差。其中基于布拉格散射的声子超材料主要对高频甚至超声频带范围[7]，而声学超材料，由于其需要附加质量，因而难以在宽频带范围内实现振动抑制效果[8]。

近年来，采用负刚度机构设计具有高阻尼和高刚度特性的复合材料或机构得到了许多学者的广泛关注[9]。应当指出，对于在隔振系统中引入负刚度元件已经有一个很长的历史， Alabuzhev等[10]对各类负刚度机构进行了详细综述。关于新型负刚度设计方法，如后屈曲梁、板、壳、预压弹簧以及磁机构也相继应用于减振装置的设计当中[11]。由于在振动系统中引入负刚度机构，系统的阻尼属性得到显著改善。Shi[12]利用磁体间的相吸和相斥配置设计了两种磁性负刚度阻尼器；Iemura等[13]将伪负刚度阻尼器应用于地震响应的控制；Dong等[14]通过采用两端平头杆的屈曲行为来实现负刚度和迟滞阻尼性能。然而，上述研究采用主动控制实现负刚度的方法来开展结构的振动控制技术研究，存在系统复杂、需外部供能和可靠性低等不足。另外，上述系统存在对作用在负载上的直接扰动的抑制效果较差。Chronopoulos等[15-16]基于线性参考振荡器采用负刚度单元设计了一种具有超阻尼特性的振荡系统，并对其仅进行了概念性设计研究。

本文提出一种采用磁性负刚度机构设计的超阻尼隔振系统，其由磁性负刚度弹簧和机械弹簧并联构成；磁体的倾斜安装方式使得系统结构更加紧凑、灵活；同时，由于在系统引入内部隐性自由度，使得该隔振系统具有高刚度、高阻尼特性，能够有效抑制作用在负载上的直接扰动并避免共振现象的产生。

1 超阻尼隔振器模型

隔振器模型如图1(a)所示，其由磁性负刚度弹簧和机械弹簧并联构成；磁性负刚度弹簧由五块沿轴向磁化的铷铁硼环形永磁体构成，处于相吸配置；上、下对称布置的环形永磁体被固定在基础上，中间的环形永磁体由两个相互对压的机械弹簧k2约束在刚性杆的两个凸台间，并使其能够沿轴向发生相对运动；连接外界被隔振物体的刚性杆通过在基础与两个凸台间分别设置两个相互对压的机械弹簧k1来为隔振系统沿轴向提供承载力。当连接物体的刚性杆沿轴向运动时，中间的环形永磁体相对刚性杆沿轴向相对运动；此时，基础上倾斜安装的环形永磁体通过吸引中间环形永磁体为隔振系统沿轴向提供与机械弹簧k1、k2方向相反的磁性恢复力和磁性负刚度；该隔振系统可简化为如图1(b)所示的具有两个自由的隔振系统；其中，z1为被隔振物体的振动位移；z2为磁性负刚度弹簧的中间环形永磁体的振动位移，即为引入的内部隐性自由度；图1(c) 为与所设计的超阻尼隔振系统具有相同静刚度kl和相同阻尼单元c的线性参考系统；图1中的系统参数分别为：m为物体质量，mc为中间环形的永磁体质量，ks为两个对压机械弹簧k1并联作用ks=2k1,ke为两个机械弹簧k2并联作用ke=2k2，kn为磁性负刚度弹簧提供的磁性负刚度，kl为线性参考系统的静刚度，c为系统的黏性阻尼，f为外部激励。

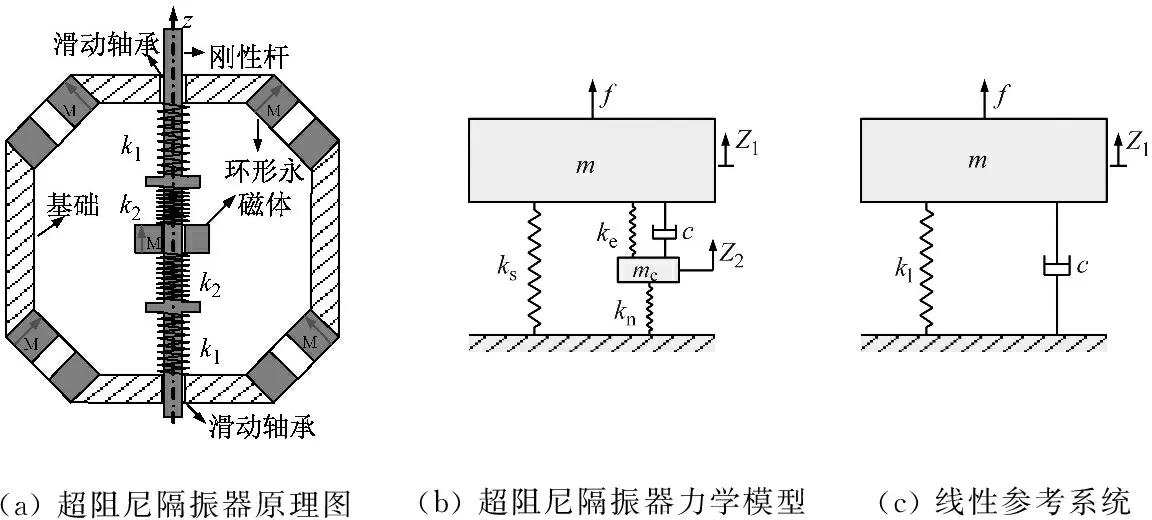
(a)超阻尼隔振器原理图(b)超阻尼隔振器力学模型(c)线性参考系统

图1 隔振器模型

Fig.1 Configuration of the isolator

1.1 动力学分析

如图1(b)所示，所考虑的超阻尼隔振器包含有磁性负刚度单元以区别于对应的线性参考隔振系统；所设计隔振系统的静刚度为

(1)

为确保所考虑系统的阻尼和隔振特性不会对结构的总刚度和承载能力造成不利影响，应使所设计系统的静刚度与对应的线性参考系统相一致，即kstatic=kl；同时，这两个隔振系统中包含有相同的阻尼单元c，因此，超阻尼隔振系统的动力学方程可表示为

(2)

外部激励f作用于隔振系统的显性自由度z1，该系统内部包含隐性自由度z2，表示中间环形永磁体的绝对位移；因此，该隔振系统是具有两个自由度的超阻尼系统，将式(2)变换到拉普拉斯域，可得

其中，式(3b)中的参数为

a4=mmc

(4a)

(4b)

(4c)

(4d)

(4e)

在式(3b)中，分母a4s4+a3s3+a2s2+a1s+a0=0为所考虑隔振系统的特征方程；式(3b)可进一步表示成具有两个实数极点和一对共轭极点的规范的传递函数形式

(5)

式中:ρ1和ρ2为特征方程的实数极点;ωn和ξn分别为所考虑隔振系统的固有频率和相对阻尼系数。为了确保所考虑系统的稳定性，由劳斯-赫尔维茨稳定性判据[17]可知

(6a)

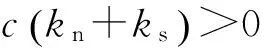
(6b)

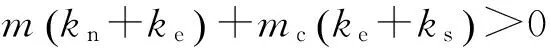
(6c)

(6d)

(6f)

a4>0⟺mmc>0

(6e)

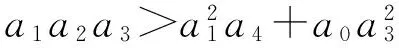
(6g)

由式(6d)、式(6e)、式(6g)自然得到满足；当式(6a)满足时，可得ke+kn>0；因而，所考虑系统的稳定性由式(6a)、式(6b)、(6f)决定。式(6f)可表示成

(7)

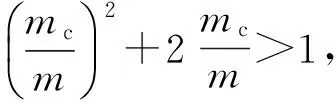
(8a)

ks>-kn

(8b)

1.2 超阻尼隔振系统参数设计

这里所讨论的超阻尼隔振系统与对应的线性参考系统具有相同的静刚度kl和阻尼单元c；因而，式(1)应满足

(9)

式(9)包含三个未知参数：ks，ke，kn；为了便于结构刚度参数优化设计，这里引入可设计参数-刚度比α为

ks=αkl

(10)

根据磁性负刚度kn<0，由式(9)和式(10)可知，α>1；当α=1时，所设计的超阻尼隔振系统退化为线性参考系统；由于在式(9)引入磁性负刚度kn，考虑到实际系统的安全稳定运行问题，引入另一个可设计的参数-安全边际ε，并满足以下条件

(11)

为了确保隔振系统能够稳定地运行，则安全边际ε>0；求解公式(9)～式(11)可得所考虑系统的设计刚度为

(12)

(13)

2 超阻尼隔振器设计参数优化

由上节分析可知，超阻尼隔振系统的刚度系数设计直接由刚度比α、安全边际ε以及对应的线性参考系统参数kl，c决定；系统的固有频率ωn和相对阻尼系数ζn可由隔振系统的特征方程求得；因此，ωn和ζn分别是参数α，ε和线性参考系统kl，c，m的函数；由式(5)可以看出，所考虑的超阻尼隔振系统可动力等效为一个具有固有频率为ωn和相对阻尼比为ζn的单自由度隔振系统；此外，根据式(11)～式(13)可知，刚度单元ks，ke，kn的数值远大于线性参考系统的支撑刚度kl，确保了系统的高刚度特性。本节将详细地讨论刚度比α，安全边际ε对所考虑系统的刚度单元ks，ke，kn，固有频率ωn以及相对阻尼系数ζn的影响。图1(c)所示的线性参考系统参数为：kl=1 500 N/m，m=2 kg，c=6 N·s/m。

2.1 超阻尼隔振系统刚度设计

由式(11)～式(13)可知，超阻尼隔振器的刚度ks，ke，kn为刚度比α，安全边际ε和线性参考系统刚度kl的函数。因而，可通过选取合适的参数α，ε来对超阻尼隔振系统的刚度单元进行优化设计。如图2(a)所示，增大ε和α可增加超阻尼隔振系统中两个相互对压机械弹簧k2(ke=2k2)的刚度系数，并且这种刚度调节与ε，α的选取呈现非线性关系；类似地，随着刚度比α和安全边际ε的增大，磁性负刚度弹簧沿轴向所提供的负刚度数值大小也以非线性增加方式增大；为了使所考虑隔振系统的静刚度与线性参考系统的支撑刚度保持一致，在结构刚度参数设计中，须选取较小的安全边际ε以满足实际的结构设计要求。

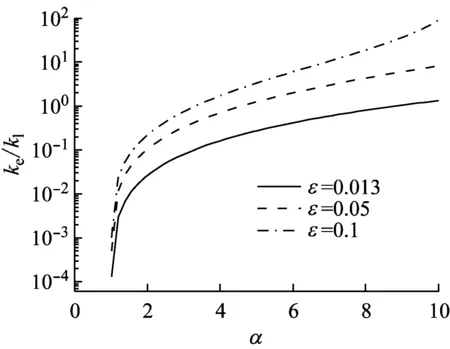
(a) α，ε对ke/kl的影响

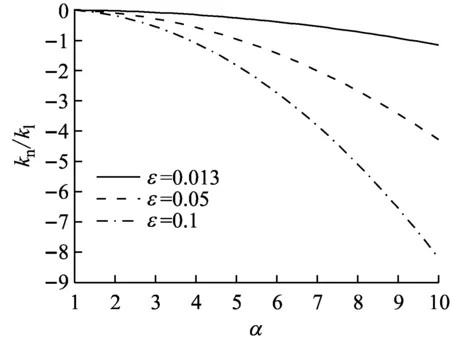
(b) α，ε对kn/kl的影响

Fig.2 The effects of stiffness ratioαand safety marginεon the stiffnesskeandknof the hyper damping system

2.2 超阻尼隔振系统阻尼分析

为实现所考虑隔振系统的超阻尼性能，需讨论结构设计参数对系统阻尼属性的影响。本文所提出的隔振系统的相对阻尼系数ζn可由特征方程求出；线性参考系统的相对阻尼系数ζ0可由式(14)求得

(14)

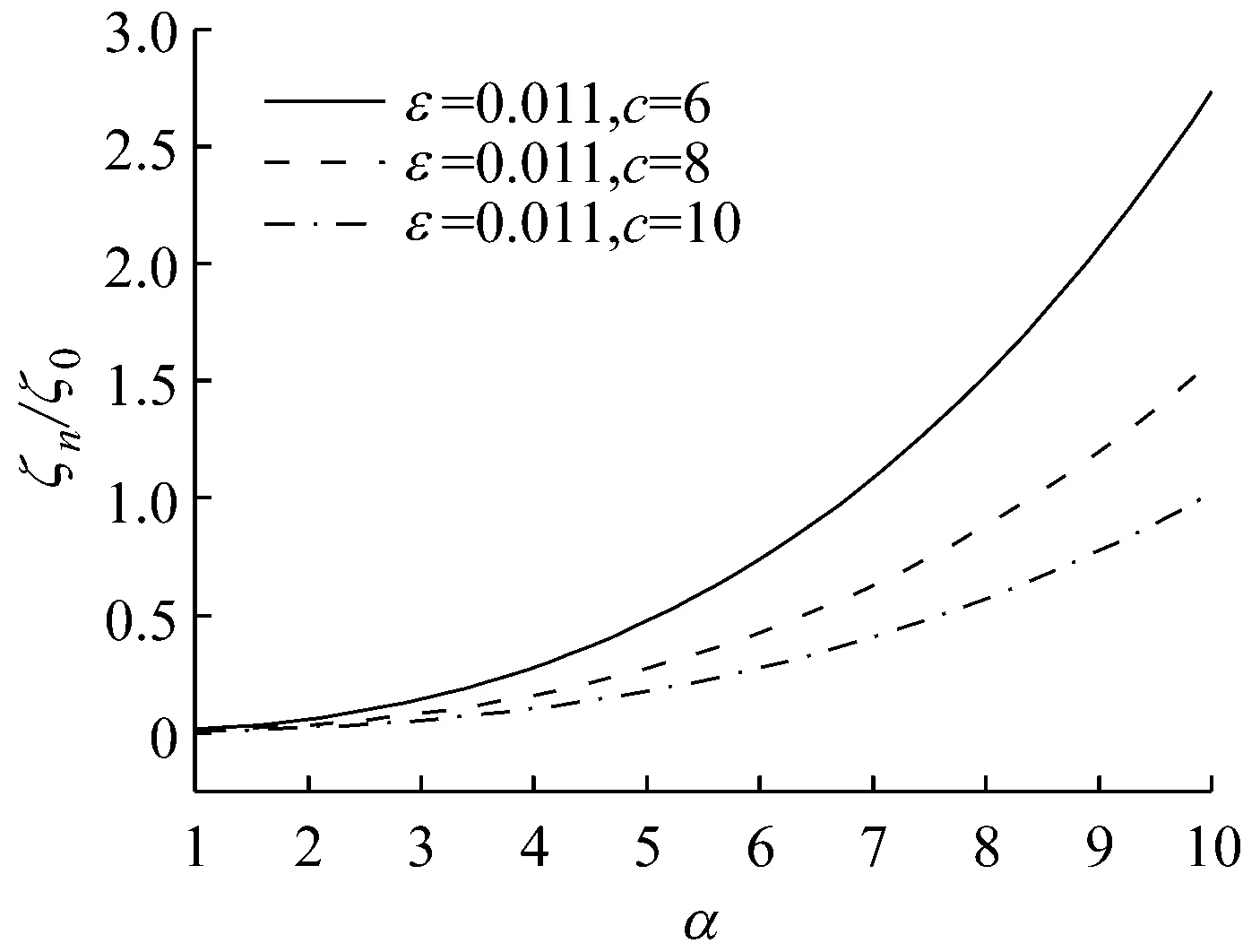
图3为刚度比α，安全边际ε以及黏性阻尼单元c对所考虑系统相对阻尼比ζn的影响。

由图3可知，随着可设计安全边际ε和刚度比α的增加，所考虑隔振系统的相对阻尼系数ζn与线性参考系统相对阻尼系数ζ0之比呈非线性增长关系，当给定刚度比α时，安全边际ε由0.005增至0.011，ζn/ζ0也随之增加；与此类似，当系统中的黏性阻尼单元c由6 N·s/m增加到10 N·s/m时，隔振系统的相对阻尼系数较线性参考系统成倍数增长，大幅度地提高了所考虑隔振系统的相对阻尼系数ζn；因此，增大α，ε以及阻尼单元c均可近似以指数形式提高隔振系统的阻尼水平，当安全边际ε选取较小的数值时，可选取设计较大的刚度比α。

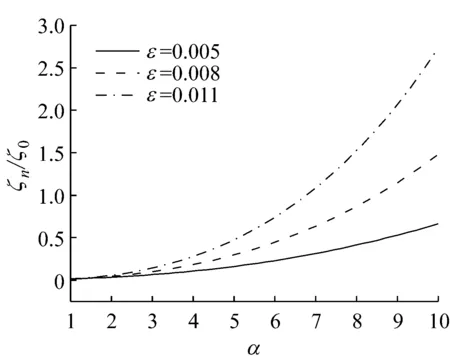
(a) α，ε对ζn的影响

(b) 阻尼单元c对ζn

Fig.3 The effects of stiffness ratioα, safety marginεand viscous dampingcon the damping ratioζnof the hyper damping system

2.3 参数优化对超阻尼隔振器固有频率的影响

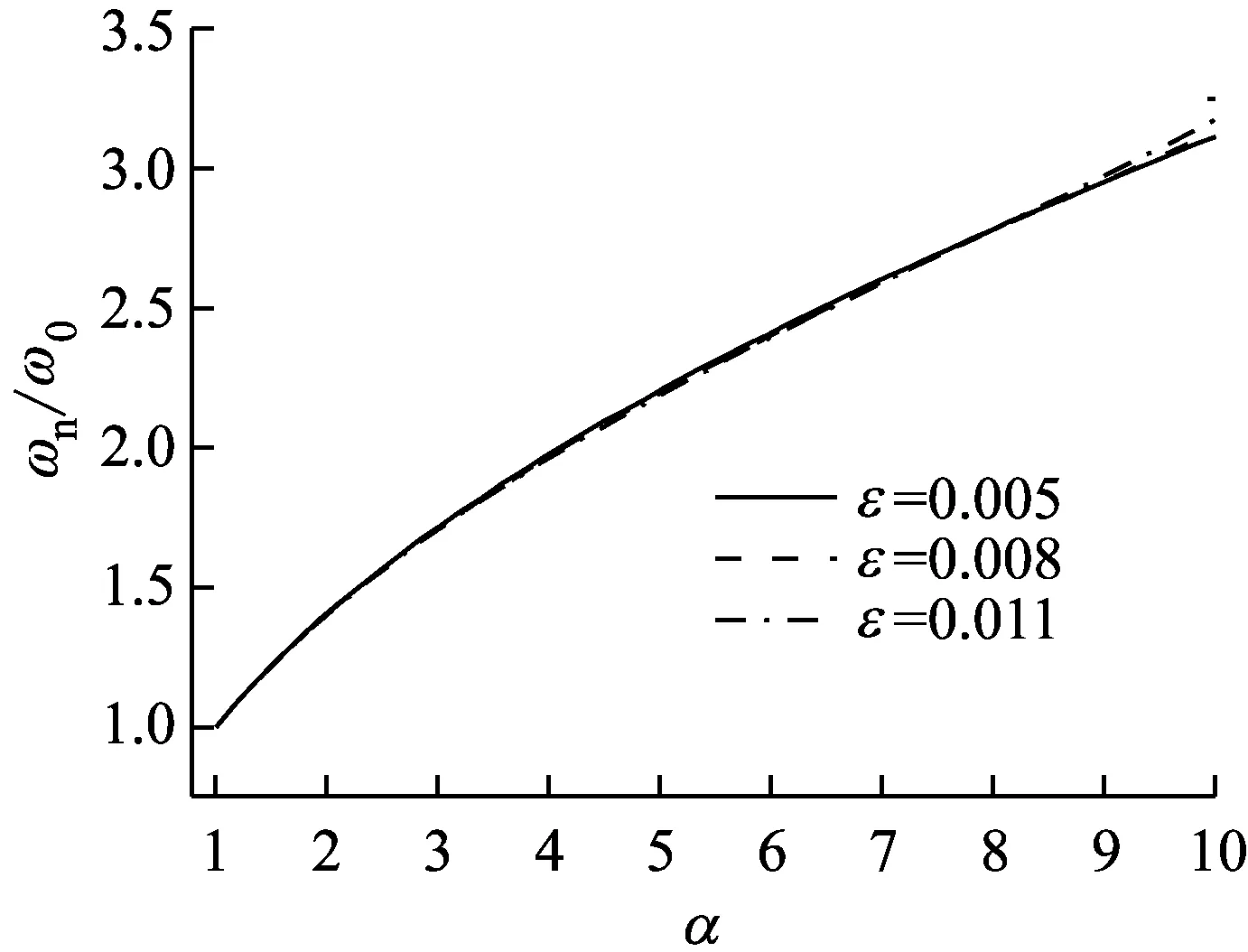
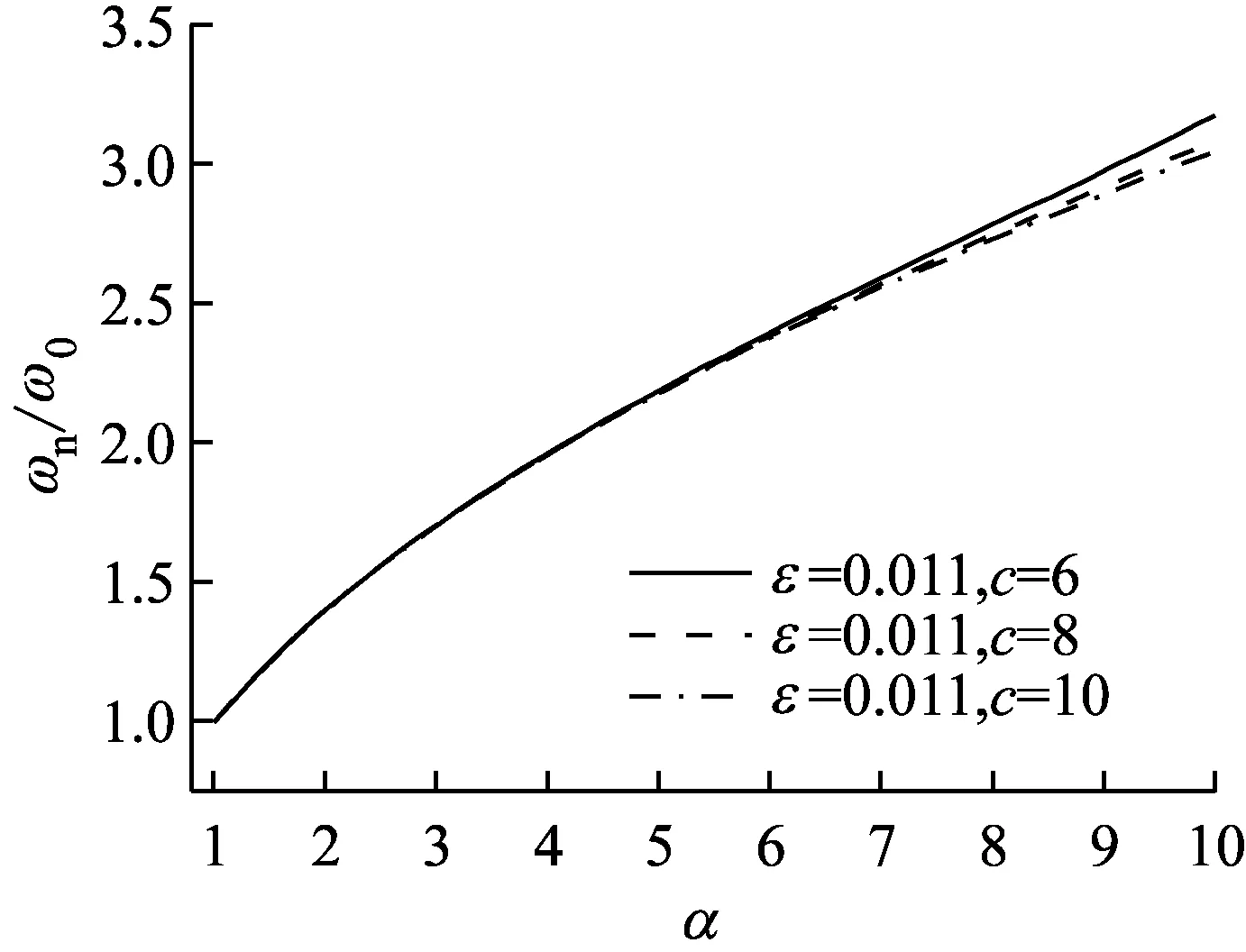
由2.2节可知，所考虑隔振系统的刚度参数ks，ke，kn均依赖于刚度比α和安全边际ε的选取；故该隔振系统的固有频率ωn同样取决于刚度比α和安全边际ε的选取设计；此外，系统的固有频率ωn可进一步由系统的特征方程求得。本节将讨论刚度比α，安全边际ε以及黏性阻尼单元c对隔振系统共振频率ωn的影响，其结果如图4所示。

由图4(a)可知，对于给定的安全边际ε，所考虑系统的固有频率ωn随着刚度比α的增加而增大，并且这种增长关系呈现非线性特征；当安全边际ε由0.005增至为0.011时，三条频率比ωn/ω0曲线与刚度比α基本重合；因此，当安全边际ε较小时，其对所考虑隔振系统固有频率ωn影响忽略。在图4(b)中，给定安全边际ε=0.011，当黏性阻尼系数c由6 N·s/m增至10 N· s/m，频率比ωn/ω0随着刚度比α的增加而增大；当α>7以后，增大黏性阻尼c，将会使得频率比ωn/ω0减小，在α<6部分，频率ωn对调节黏性阻尼c不敏感。

(a) α,ε对ωn/ω0的影响

(b) 阻尼单元c对ωn/ω0的影响

基于以上相关分析，为满足实际工程设计的要求，在进行超阻尼隔振系统参数设计时，要求安全边际ε→0+且刚度比α满足1<α，本文中取α=8，ε=0.011。

3 磁性负刚度弹簧磁力与刚度分析

由于磁结构间的相互作用，既可以提供正刚度，也可以实现负刚度性能。本文采用倾斜磁体相吸配置构成磁性负刚度弹簧；由于其结构的对称性，采用右半边对称结构进行分析，如图5所示；上、下1号环形永磁体倾斜固定，其中心位置分别为(0，d，±H)，相对水平方向倾斜角度α；2号环形永磁体沿轴向发生向对运动；所采用的环形永磁体几何参数如表1所示。

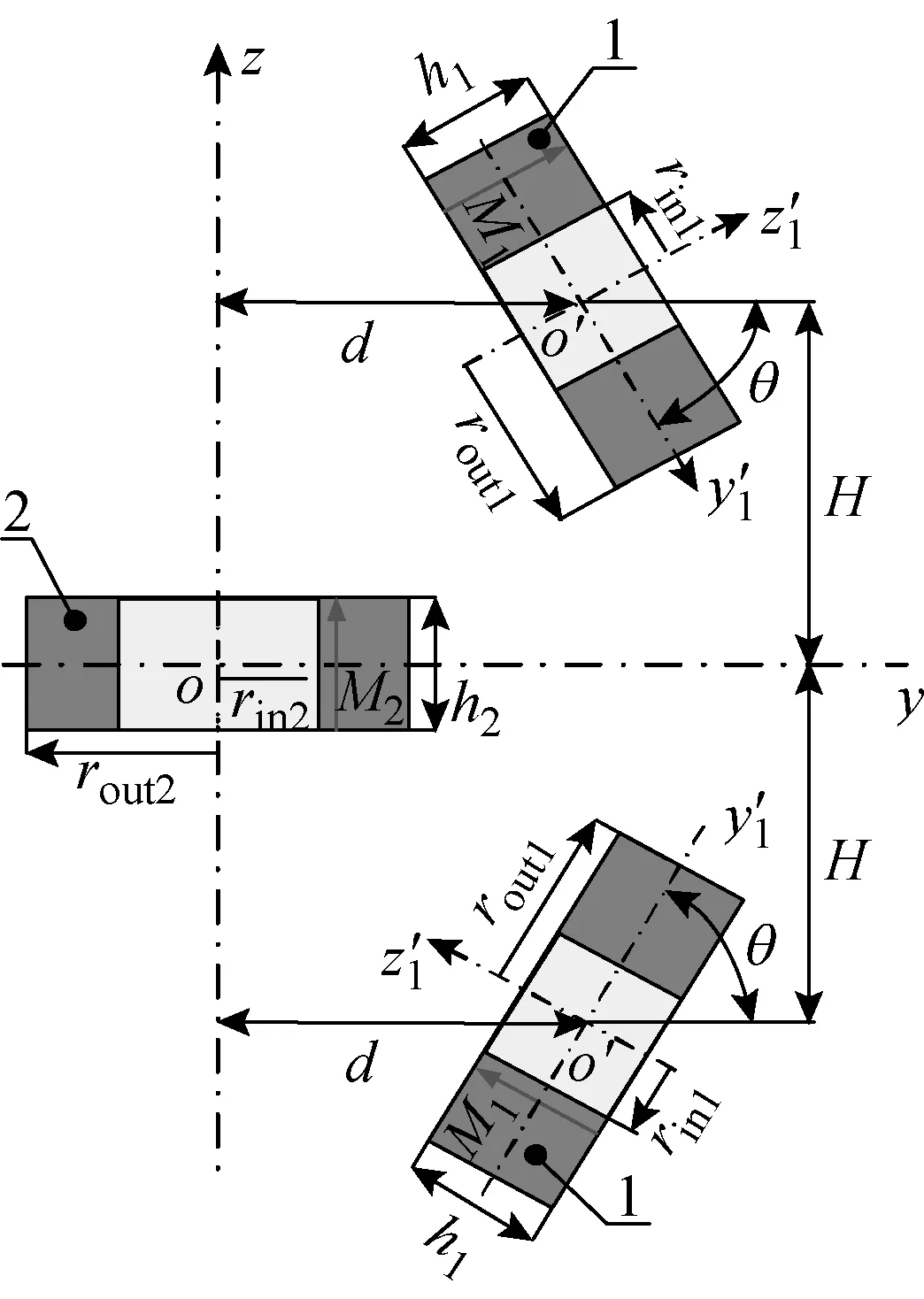
图5 磁性负刚度弹簧模型

这里假定环形永磁体沿其轴向均匀磁化，磁化强度分别为M1，M2；磁化强度可由剩余磁感应强度Br1，Br2求得：M1=Br1/μ0，M2=Br2/μ0，μ0为真空磁导率。根据分子电流假说，永磁体磁矩可表示成由体电流和面电流构成[18]，永磁体的体电流密度和面电流密度分别为

(15)

js=M×en

(16)

式中，en为磁体表面的外法线方向。由于永磁体均匀磁化，根据式(16)可知，环形永磁体的体电流密度为0；只在永磁体的内、外圆柱表面具有非零的面电流密度

表1 环形永磁体参数

(17)

式中，φ为内、外圆柱表面环向单位向量。根据毕尔—沙伐定律和安培力定理[19]，可求得图5中上面1号倾斜环形永磁体作用在沿轴向运动的2号环形永磁体上的磁力Fu和磁刚度Ku分别为

(18)

(19)

其中，在式(18)和式(19)中的被积函数Φ1，Φ2，Φ3，Φ4，Φ5，Φ6，Φ7，Φ8分别为

式中，z(1)=-h2/2，z(2)=-h2/2，z为中间2号环形永磁体沿轴向的位移。

类似地，同样可求得下面1号倾斜环形永磁体作用在2号环形永磁体上的磁力Fb；因此，一对倾斜的1号环形永磁体作用在的2号环形永磁体上的磁力为

Fm=Fu+Fb

(20)

将式(20)对2号环形永磁体沿轴向位移z求一阶导数，则可得由2号环形永磁体与一对倾斜的1号环形永磁体构成的磁性负刚度弹簧沿轴向提供的磁性负刚度为

(21)

当基础上安装有2对对称的上下倾斜1号环形永磁体时，磁性负刚度弹簧沿轴向所提用的负刚度数值大小为2倍的式(21)，其负刚度曲线如图6所示。

由图6可知，当中间环形永磁体的振动位移被限制在±2.5 mm范围内，该磁性负刚度弹簧的负刚度近似为一常数；在平衡位置附近，增大倾斜角α，负刚度数值增加。

4 超阻尼隔振器响应分析

根据显性自由度z1在拉氏域下的传递函数形式，可由式(3b)获得主振系统z1在傅氏域下的频响函数为

(22)

并由式(3a)可得频响Z2/F为

(23)

当磁性负刚度弹簧中的中间环形永磁体质量与被隔振物体质量之比μ=mc/m分别为0.015 9，0.025时，超阻尼系统响应曲线Z1/F如图7所示。所考虑的隔振系统在引入不同质量的中间环形永磁体作用下，主系统的振动响应在整个频带范围内被有效地抑制且均<0 m/N。对比对应线性难考系统，超阻尼主系统在低频频带范围(<10 Hz)内的振动被有效地抑制，并避免了系统在低频范围内出现共振。在频率13 Hz附近，系统出现了<0 m/N的共振峰；在高频频带范围内，主系统的振动响应收敛于线性参考系统。

当物体受到外部激励f作用时，表示物体振动状况的显性自由度z1沿轴向产生振动位移；同时，由相互对压机械弹簧k2约束的中间环形永磁体将会相对刚性杆发生沿轴向运动；因此，物体的一部分振动能量被转移到磁性负刚度弹簧中的中间环形永磁体上，其振动能量将进一步被黏性阻尼c以热能的形式耗散；因此，外部激励f引起的中间环形永磁体振动响应将采用传递比Z2/F来描述，由式(23)可得频率响应Z2/F如图8所示。

图6 磁性负刚度曲线

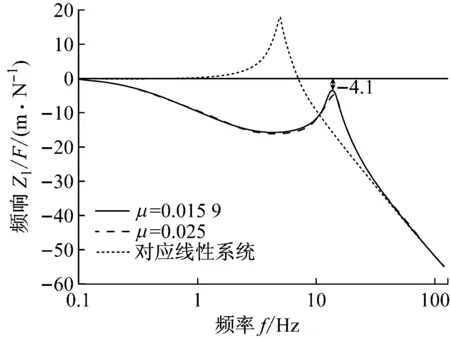
图7 不同的质量比μ，频响Z1/F分析：刚度比α=8，安全边际ε=0.011，黏性阻尼系数c=6

Fig.7 Analysis of frequency responseZ1/Ffor various mass ratioμ: all calculation conducted withα=8,ε=0.011 andc=6

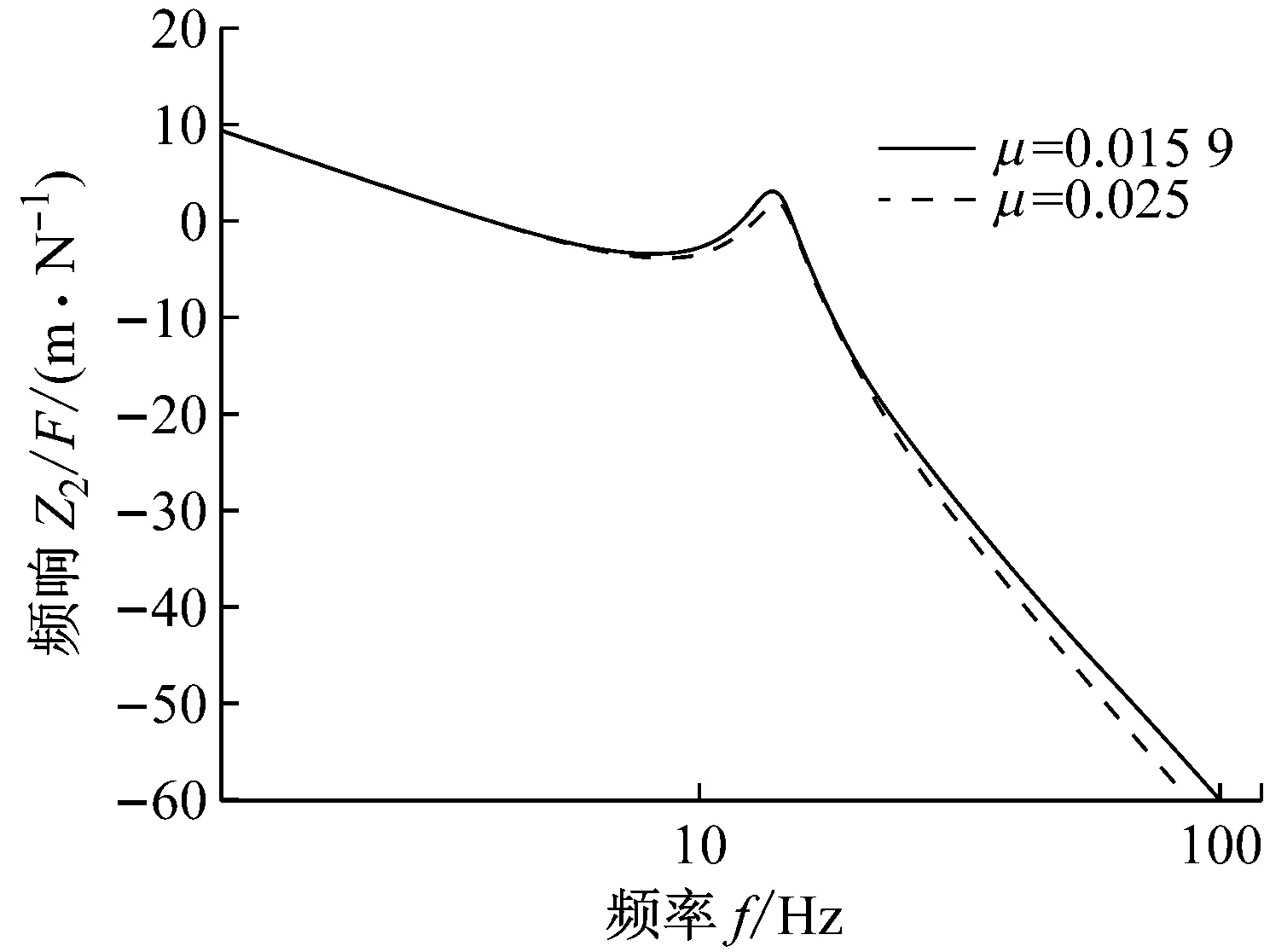
图8 不同的质量比μ，频响Z2/F分析：刚度比α=8，安全边际ε=0.011，黏性阻尼系数c=6

Fig.8 Analysis of frequency responseZ2/Ffor various mass ratioμ: all calculation conducted withα=8,ε=0.011 andc=6

在低频区域，中间环形永磁体的振动较为剧烈，是由于被隔振物体在低频区域的一部分振动能量转移到中间环形永磁体上所致；当引入的中间环形永磁体质量变化时，μ由0.015 9增至0.025，共振峰位于13 Hz附近；该现象与图7中的<0 m/N的共振现象相一致，是由引入的中环形永磁体所产生；同时，增加中间环形永磁体质量将会提高Z2/F在高频部分的衰减率。此外，图9为中间环形永磁体与被隔振物体在振动过程中幅值之比|Z1/Z2|；在低频部分，中间环形永磁体振动幅值远大于被隔振物体。在高频部分，随着质量比μ的增加，隐性自由度z2相对显性自由度z1的振动会慢慢减小，其振动能量是被与隐性自由度z2相连的黏性阻尼单元c所消耗。

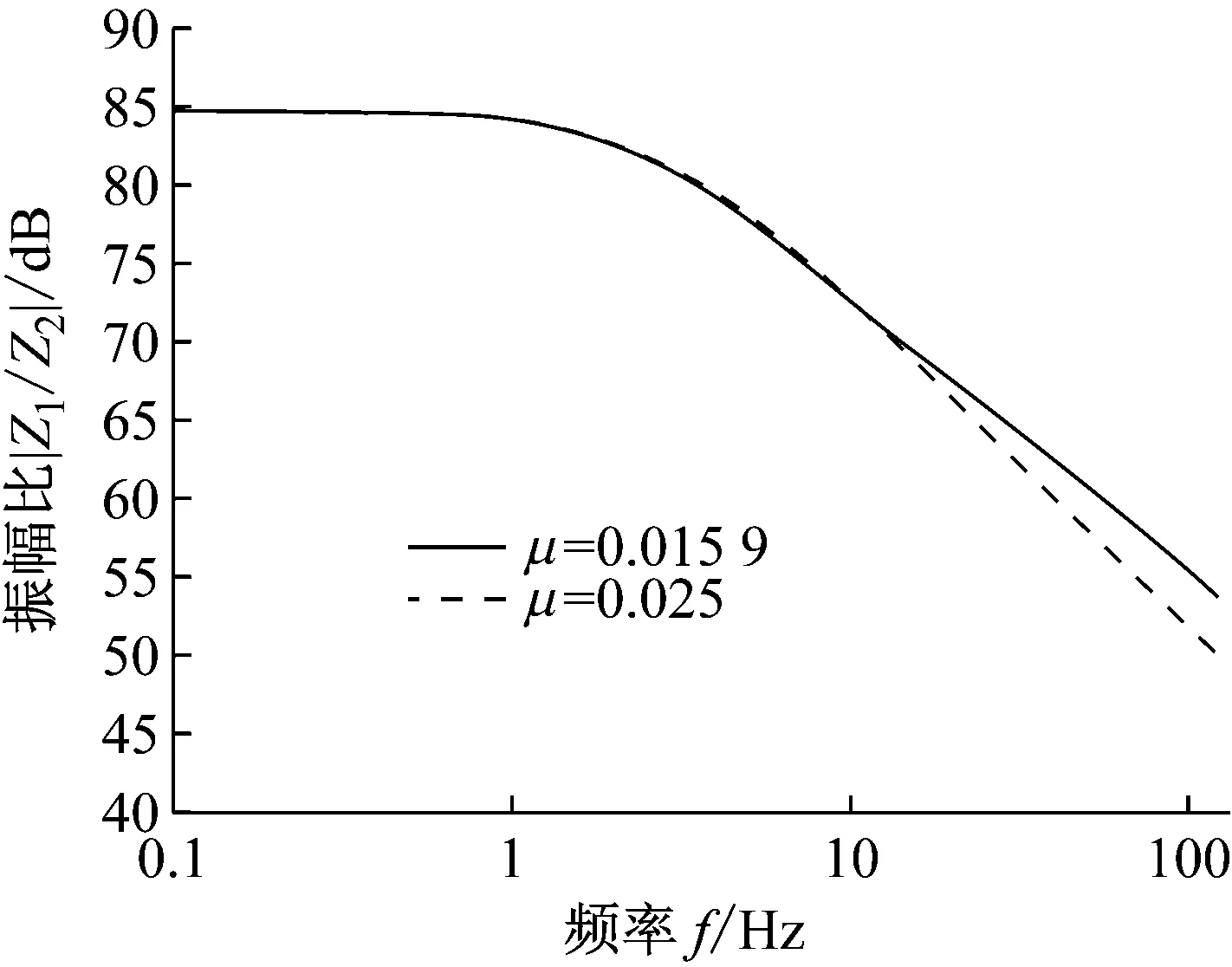
图9 不同的质量比μ，幅值|Z2/Z1|随频率f的变化：刚度比α=8，安全边际ε=0.011，黏性阻尼系数c=6

Fig.9 Analysis of the response |Z2/Z1| for various mass ratioμ: all calculation conducted withα=8,ε=0.011 andc=6

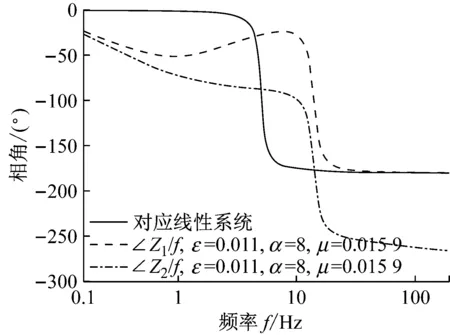
图10 相角∠Z/f，∠Z1/f及∠Z2/f分析：刚度比α=8，安全边际ε=0.011，黏性阻尼系数c=6

Fig.10 Analysis of phase angle∠Z/f, ∠Z1/fand ∠Z2/f: all calculation conducted withα=8,ε=0.011 andc=6

5 结 论

本文通过采用倾斜磁体构成磁性负刚度弹簧，将中间环形永磁体沿轴向的自由度释放引入一个内部隐性自由度，并由相互对压的机械弹簧约束使其沿轴向相对运动，设计了一种新型超阻尼隔振系统；通过与线性参考系统对比，讨论了所考虑系统的结构参数优化设计方法，分析了其动力学频响特性，探讨了其超阻尼特性以及振动抑制机理。研究结果表明：通过结构的优化设计，可使所考虑隔振系统具有超阻尼特性，隔振系统的弹性单元具有高刚度特性；由中间环形永磁体引入的附加质量将有助于提高系统的阻尼特性；在线性参考系统共振峰附近，超阻尼隔振系统的衰减率在低频范围内达到极值；该系统阻尼特性的提高是由于正负刚度弹性元件所提供的弹性恢复力间存在相位差；因此可直接抑制作用在物体上的直接扰动，并避免了系统的共振。

[1] RIVIN E I. Passive vibration isolation[M]. New York: Applied Mechanics Reviews, 2003.

[2] 丁文镜. 减振理论[M]. 北京：清华大学出版社, 1988.

[3] 熊伟, 刘耀宗, 邱静, 等. 材料阻尼模型综述[J]. 功能材料, 2006, 36(10): 1497-1500.

XIONG Wei, LIU Yaozong, QIU Jing, et al. Review of models about material damping[J]. Functional Materials, 2006, 36(10): 1497-1500.

[4] LAKES R S. Extreme damping in compliant composites with a negative-stiffness phase[J]. Philosophical Magazine Letters, 2001, 81(2): 95-100.

[5] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L. Acoustic band structure of periodic elastic composites[J]. Physical Review Letters, 1993, 71(13): 2022-2025.

[6] SIGALAS M, ECONOMOU E. Band structure of elastic waves in two dimensional systems[J]. Solid State Communications, 1993, 86(3): 141-143.

[7] HUSSEIN M I, LEAMY M J, RUZZENE M. Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4): 040802.

[8] LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289: 1734-1736.

[9] JAGLINSKI T, KOCHMANN D, STONE D. Composite materials with viscoelastic stiffness greater than diamond[J]. Science, 2007, 315: 620-622.

[10] ALABUZHEV P, RIVIN E I. Vibration protection and measuring systems with quasi-zero stiffness[M]. Florida: CRC Press, 1989.

[11] IBRAHIM R A. Recent advances in nonlinear passive vibration isolators[J]. Journal of Sound and Vibration, 2008, 314(3/4/5): 371-452.

[12] SHI X, ZHU S Y. Magnetic negative stiffness dampers[J]. Smart Materials and Structures, 2015, 24(7): 072002.

[13] IEMURA H, PRADONO M H. Advances in the development of pseudo-negative-stiffness dampers for seismic response control[J]. Structural Control & Health Monitoring, 2009, 16(7/8): 784-799.

[14] DOMG L, LAKES R. Advanced damper with high stiffness and high hysteresis damping based on negative structural stiffness[J]. International Journal of Solids and Structures, 2013, 50(14/15): 2416-2423.

[15] ANTONIADIS I, CHRONOPOULOS D, SPITAS V, et al. Hyper-damping properties of a stiff and stable linear oscillator with a negative stiffness element, Journal of Sound and Vibration, 2015, 346: 37-52.

[16] CHRONOPOULOS D, ANTONIADIS I, COLLET M, et al. Enhancement of wave damping within metamaterials having embedded negative stiffness inclusions[J]. Wave Motion, 2015, 58: 165-179.

[17] 卢伯英, 于海勋, OGATA K. 现代控制工程[M]. 北京：电子工业出版社, 2000.

[18] 冯慈璋, 马西奎. 工程电磁场导论[M]. 西安：高等教育出版社, 2000.

[19] FURLANI E P. Permanent magnet and electromechanical devices: materials, analysis, and applications[M]. New York: Academic Press, 2001.

Design of a high stiffness and hyper-damping vibration isolator based on negative stiffness mechanism

DONG Guangxu, ZHANG Xinong, XIE Shilin, LUO Yajun, ZHANG Yahong

(State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China)

In order to isolate direct disturbances exerted on payload and to improve damping properties of an isolation system for purpose of avoiding resonances, a hyper-damping vibration isolator was developed based on a magnetic negative stiffness mechanism. The mechanism consisted of a magnetic negative stiffness spring (MNSS) and two pairs of pre-pressured mechanical springs. MNSS included five magnetic rings axially magnetized, inclined magnetic rings were symmetrically mounted on the base, while a moving ring was constrained by two pre-pressured mechanical springs and was allowed to oscillate along the axial direction. The analytical expressions for magnetic restoring force and magnetic negative stiffness were further deduced according to the current model. By repositioning the stiffness and damping elements of the vibration isolation system, the vibration isolation system was deigned to be a hyper-damping device with the same static stiffness, the same damping and the same mass as those of a typical linear reference system. The impacts of stiffness elements, damping ones of the device and added mass of magnet on the damping, natural frequencies of the designed system and vibration responses of the main system were deeply analyzed. The results showed that the proposed vibration isolation system has high stiffness and hyper damping characteristics and it can effectively suppress vibrations of the main system; the response of the main system converges to that of the linear reference system in a higher frequency range.

hyper-damping; high stiffness; negative stiffness; vibration isolation

国家自然科学基金项目(11172225)

2016-01-11 修改稿收到日期：2016-03-21

董光旭 男，博士，1988年生

张希农 男，博士，教授，1954年生

V214.3+3

A

10.13465/j.cnki.jvs.2017.09.035