基于圆域分析的大型回转支承初期故障诊断

封 杨， 黄筱调， 洪荣晶， 陈 捷

(南京工业大学 机械与动力工程学院， 南京 210009)

基于圆域分析的大型回转支承初期故障诊断

封 杨， 黄筱调， 洪荣晶， 陈 捷

(南京工业大学 机械与动力工程学院， 南京 210009)

为解决真实工况下大型回转支承振动信号背景噪声大、常用故障诊断方法难以适用的问题，提出了一种基于圆域分析的振动信号处理方法。将时域信号进行圆域转换，并按一定角度将转换后的圆域信号划分成多个区域；判断各区域信号邻域相关离散点拟合椭圆的倾角方向，得到回转支承整圈对应的多个异常向量；以异常向量的平均向量作为圆域分析的特征向量，分析其均值、方差、歪度和峭度指标的变化情况，实现回转支承的故障诊断。对某型号回转支承进行了加速寿命试验，结果表明，该方法能够有效诊断出回转支承滚道的区域滑移、点蚀等初期故障，相比常见的时域特征、小波分析等方法准确度更高，故障可识别度更强，因此可以用于实际工况下回转支承的故障诊断。

回转支承；圆域分析；圆域重采样；故障诊断；加速寿命试验

大型回转支承作为重要的回转连接件被广泛使用在风力发电机、港口机械、建筑工程机械等大重型机械中，其滚动体中心圆直径通常超过600 mm，内圈或外圈会加工出整圈齿轮用于驱动。国家标准对回转支承的可靠性提出了很高的要求[1]，但近年来由于回转支承的失效导致的机器停机事故屡见不鲜，而回转支承的制造、运输、吊装的周期很长且花费巨大，风机一次的吊装成本可达数十万，港口机械的停机带来的损失更是难以估量。因此，大型回转支承的故障诊断尤其是初期故障的判别尤为重要。

轴承的典型性能退化过程一般如下：初始会有一个磨合过程，然后在较长时间段内运行相对平稳，到中后期轴承的局部滚道产生裂纹、点蚀等初始故障后，性能很快衰退直至完全失效[2]。大量的专著和文献对转速>600 r/min、外圈直径<500 mm的中高速轴承的故障诊断方法进行了深入地研究和探讨，此类轴承故障时的振动信号冲击成分明显，信噪比高，因此各种方法在试验或应用中都得到了有效的验证。但是，大型回转支承体积庞大，转速通常<10 r/min，有时可低至1 r/min，滚道与滚动体接触时产生的冲击成分非常微弱，振动信号中有效信息被高频噪声完全淹没，这使得同样的诊断方法应用在大型低速的回转支承振动信号中效果并不理想[3]，给其故障诊断带来了很大的挑战[4]。

尽管如此，大型回转支承的故障诊断近年来依然受到了大量学者的关注。Zvokelj等[5-6]先后提出集合经验模态分解-多分辨主成分分析(Ensemble Empirical Mode Decomposition-Multi-Scale Principal Component Analysis, EEMD-MSPCA)和集合经验模态分解-多分辨核主元分析(EEMD-MSKPCA)的降噪方法用于回转支承振动信号，并利用PCA/KPCA(Principal Component Analysis/Kernel PCA)模型准确诊断出回转支承的滚道故障。郭刚涛等[7]将混沌理论用于大口径天线中的回转支承故障诊断，利用Lyapunov指数识别出回转支承的滚道点蚀故障。赵阳等则采用了经验模态分解(Empirical Mode Decomposition，EMD)和独立分量分析(Independent Component Analysis，ICA)相结合的盲源分离方法，从盲源信号的功率谱中分析出回转支承故障特征频率。杨杰等提出了小波-能量模式的回转支承诊断方法，从加速寿命试验的振动信号中分离出了故障频率。然而，文献[8]中回转支承的滚道故障均是人工加工出的严重缺陷，并不符合回转支承自然性能退化过程中产生的诸如点蚀、裂纹、剥落等故障，而文献[9]中的加速寿命试验超载了90倍，这在工程实际中也较为罕见。此外，上述文献中的振动信号中均能明显观察到高频冲击成分，与回转支承真实工况下振动信号的特征也不甚相符。

由以上可知，现有的回转支承故障诊断方法多是针对振动信号的时域、频域或者时频域进行分析，此类方法对严重故障或是寿命试验中后期的振动信号的处理非常有效，但是仍然很难用于实际工况下回转支承的故障尤其是初期故障的诊断。相比之下，振动信号的一些特征在圆域内与在时域、频域内有着截然不同的呈现方式，圆域采样及相关的圆域分析近年来越来越多地被用于轴承[10-11]、风机[12-13]、齿轮箱[14]等故障诊断中，而Caesarendra等[15]将其应用于回转支承状态监测，取得了较为理想的效果。本文将进一步探讨振动信号的圆域分析方法，并将其用于大型回转支承的初期故障诊断。

1 背景知识

1.1 PAA与邻域相关图

轴承振动信号的采样频率很高，即使是转速极低的回转支承，其采样率通常>1 kHz，如此庞大的数据量将显著影响故障诊断模型的计算效率，使其很难应用到实时状态监测系统中。因此，有必要对原始振动信号的数据量进行缩减。分段累积近似法(Piecewise Aggregate Approximation, PAA)作为一种数据缩减方法，最初由Yi等[16]提出，其特点是在对大量时域数据进行缩减的同时尽可能多地保持数据的原有特征。PAA实现较为简单，对于一组有L个数据样本的序列y=(y1,y2,…,yL)，首先定义一个常数w，w应为L的约数，然后将样本序列y等分成N段，N=L/w，最后将每段序列的代数平均值连起来便得到缩减后的新序列Y=(Y1,Y2,…,YN)，其中每个元素的计算公式为

(1)

式中，w又被称为PAA窗的大小，显然w越大，缩减后的数据量就越小，但是丢失的信息也就越多。

除了缩减数据量外，PAA另一个重要的应用是检测振动信号中频率的变化，为此需要引入邻域相关的概念。邻域相关即是将数据缩减后的时域序列Y以邻域相关图的方式呈现，图中每个坐标点的横坐标为Yn，纵坐标为Yn+1，n∈[1,N-1]。将时域振动信号先进行PAA，然后利用直接椭圆拟合法[17]对邻域相关离散点进行椭圆拟合的过程称为PAA过程。为研究其检测信号中频率变化的有效性，产生两组幅值为1、频率分别为1 Hz和4 Hz的标准正弦波形，其采样率fs均为48 Hz，采样时间均为1 s，令w=4，则两组波形的PAA及邻域相关图，如图1所示。

(a) 1 Hz正弦信号

(b) 4 Hz正弦信号

图1 两组仿真信号的PAA及邻域相关图

Fig.1 PAA and neighborhood correlation of two simulated signals

由图1可知，正弦信号的邻域相关图可拟合出近乎完美的椭圆，但在PAA窗大小w和采样率fs相同的情况下，不同频率的正弦波拟合出的椭圆具有不同的倾角，定义图1(a)中倾角为0～π/2的椭圆为右倾斜椭圆，图1(b)中倾角为π/2～π的椭圆为左倾斜椭圆。PAA过程正是通过椭圆的倾角判断出信号中频率的变化。实际上，回转支承早期振动信号中的有效成分几乎完全被背景噪声淹没，高频白噪声占主导，而随着故障的产生和加剧，周期性地冲击信号会越发明显，信噪比会提高，此时信号中的中低频成分占主导。因此，可将PAA过程用于回转支承的状态监测，通过拟合椭圆倾角的变化诊断出回转支承潜在的早期故障。

1.2 圆域重采样

圆域(又称角度域)分析最初由Luo等[18]提出，用以解决转动部件变转速工况下振动信号分析频谱泄漏的问题。圆域分析的核心思想是将时域振动信号映射到角度域，消除振动信号中的时间属性，进而消除转速对振动信号分析的影响。获取圆域振动信号的方法有两种：阶次追踪法[19]和圆域重采样。阶次追踪法通常采用专用仪器直接进行圆域采样，而圆域重采样则是通过坐标变换将时域信号转换成圆域信号。

假设回转支承转动β(0°<β≤360°) 角度需要Ts，时间序列为t=[1,2,…,T]，则其对应圆域内的弧度序列为

(2)

将转换后的弧度及其对应的振动幅值在三维空间展开，便可得到时域信号的圆域表达。以图1(b)中4 Hz的正弦信号为例，若其对应的回转支承转动的角度是360°，则圆域重采样后的信号，如图2所示。

(a) 时域信号

(b) 圆域信号

由前文可知，PAA过程能够有效识别振动信号中主要频率成分的变化，并可用于回转支承的故障诊断，但实际应用中PAA过程所处理的数据量(即序列y的长度)及其对应的物理意义并未给出。在状态监测系统中，一次PAA过程处理数据量越少，总数据量一定的情况下需要执行PAA过程的次数就越多，系统计算负荷会大幅提升，而一次PAA过程处理数据量越大，信号中的频率成分就越复杂，拟合椭圆对信号中频率变化的敏感度会有所降低。因此，确定合适的一次PAA过程处理的数据量及其对应的物理意义非常重要。本文将利用圆域重采样将时域信号转换成圆域信号，忽略转速对信号处理的影响，同时将圆域信号按一定角度均分，并对每段信号执行PAA过程，最终通过相应的圆域分析实现故障诊断。

2 圆域分析故障诊断方法

2.1 故障诊断流程

本文针对大型回转支承提出的基于圆域分析的故障诊断流程，如图3所示，对于一段时域振动信号，首先通过圆域重采样的方法将其转换成圆域信号，同时按照一定角度将圆域信号均分成多个区域，并对每个区域的信号执行PAA过程，然后通过邻域相关图中拟合椭圆的倾角方向确定各区域是否出现异常，最后计算整段圆域信号的相关特征，并监测其在时域上的变化趋势，进而实现回转支承初期故障诊断。

图3 故障诊断流程图

具体而言，若振动信号特征频率为fc、采样率为fs，回转支承转速为qr/min，则回转支承转动一周对应着60/qs的振动信号，每秒钟的振动信号对应圆域内的角度为(6·q)°。因此，可将0～60/qs的时域振动信号转换成0°～360°的圆域信号，同时每隔(6·q)°将其分割成60/q个角度区域(每个区域对应1 s的振动信号)，然后对每个区域的信号执行PAA过程。然而，由前文可知，PAA过程中窗大小w与采样率fs、信号特征频率fc之间存在某种联系，w选取是否合适直接决定了PAA过程识别异常信号的能力，其详细的优化方法将在“2.2”节中给出。此外，由图1可知，在同一PAA过程下，高频信号的拟合椭圆是左倾斜的，当信号频率降低时，椭圆转换成右倾斜的，考虑到回转支承初期振动信号中主要是高频白噪声，对应的拟合椭圆应当是左倾斜的，而到中后期振动信号中的中低频率能量较高，其拟合椭圆应当是右倾斜的。据此，将PAA过程中拟合椭圆为右倾斜的角度区域定义为异常区域并标记，同时作出对应的异常向量，如图4所示。

图4 圆域分析中的异常向量

图4将回转支承一周划分成8个区域，对应的转速q=7.5 r/min，在90°和315°的区域检测出异常，作出异常向量V1和V2，然后计算所有异常向量的平均向量得到圆域分析的特征向量Vmean。最后，在状态监测系统中，回转支承每转过一周，可实时计算其振动信号的圆域特征向量Vmean，并求得Vmean在圆域内的均值、方差、歪度和峭度指标作为故障诊断的依据，具体计算过程将在“2.3”节中给出。

2.2 PAA窗大小w的优化

由“1.1”节可知，执行PAA过程首先需要确定合适的PAA窗大小w，在同一采样率fs下，不同的w取值会导致同一段信号拟合出不同倾角方向的椭圆。另一方面，w取定后，不同特征频率fc的信号也会拟合出不同倾角的椭圆。因此，必然存在某个因变量λ随着w、fc和fs而改变，控制着拟合椭圆的倾角，当λ达到临界时椭圆从一个倾角方向转变为另一个方向，其经验计算公式可定义为

(3)

设定fs=2 048 Hz，将fc在0～300 Hz变化，w在2～8取值并对频率为fc的正弦信号执行PAA过程，确定拟合椭圆的倾角方向，最终得到的关系模型如图5所示。

由图5中可知，λ与fc呈线性关系，当λ>0.25时，PAA过程拟合出的椭圆是左倾斜的，当λ<0.25时，拟合椭圆是右倾斜的，当λ=0.25时，PAA过程拟合出的实际上是没有倾角的圆。因此，λ又可称为转换系数，0.25是其阈值。另一方面，当w确定后，每条曲线在λ阈值处都有一个交点，这个点的频率被称为转换频率，即当信号的频率高于此频率时，椭圆是左倾斜的，当信号的频率低于此频率时，椭圆是右倾斜的，这与图1中观察到的现象是一致的。

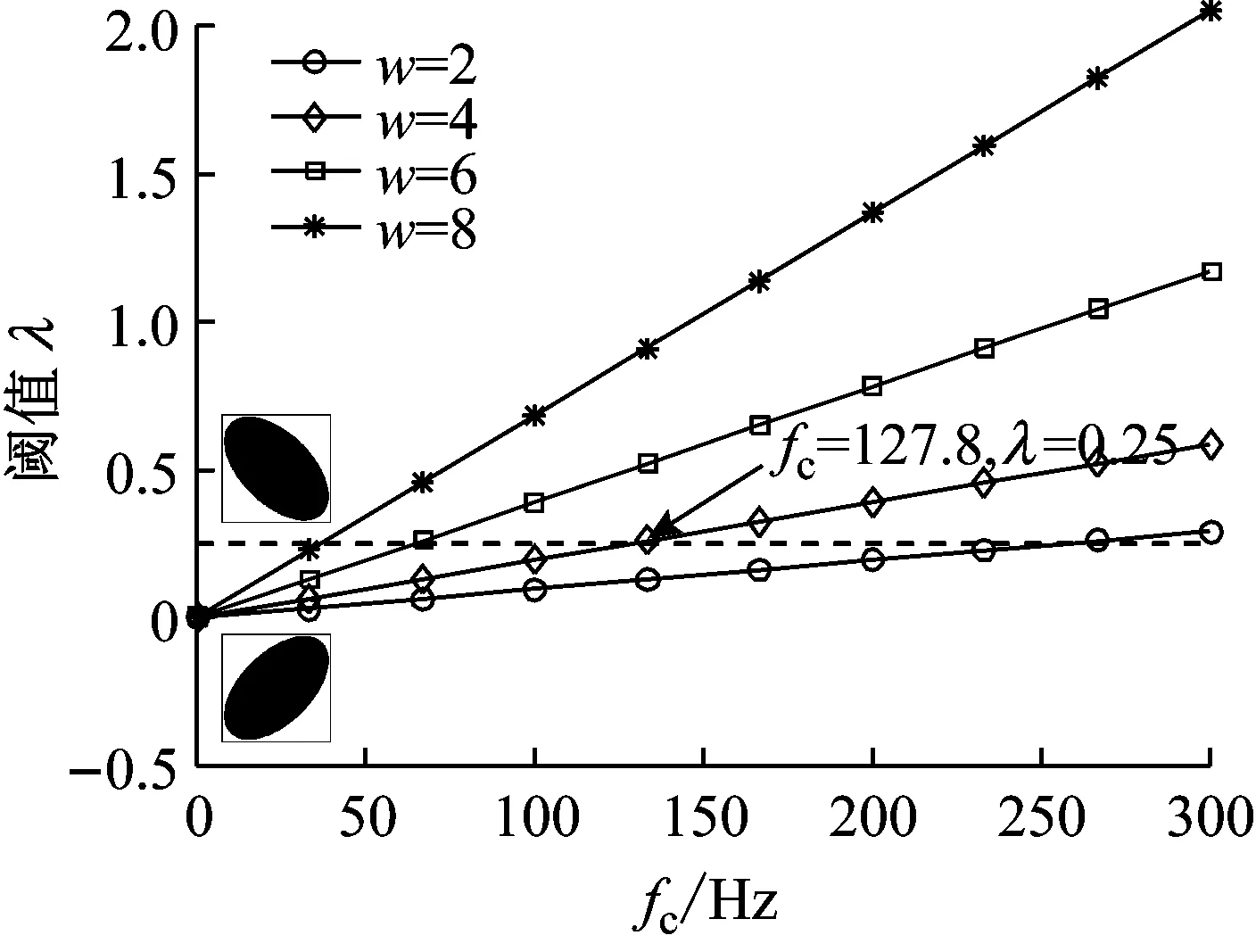
图5 转换系数λ与转换频率fc的关系

如前所述，回转支承运行初期的振动信号中多是高频噪声，此时拟合椭圆是左倾斜的，到中后期振动信号中出现异常时中低频占主要成分，此时拟合椭圆会出现右倾斜的。因此，工程实际中可先确定信号出现异常时大致的频率范围，再由此确定最接近的转换频率，最终确定最优的w取值。

2.3 圆域特征计算

假设信号异常识别步骤中作出的异常向量为V1,V2,…,VM，各向量在圆域内的角度为θ1,θ2,…,θM，则各异常向量可用复数表达为

Zm=r·(cosθm+isinθm)=r·eiθm

(4)

式中：m∈[1,M]；r为各异常向量的模长，此处均为单位1。由此可知，圆域分析的特征向量Vmean的表达式为

(5)

其所在圆域的角度θmean应为

θmean=Angle(Zmean)

(6)

据此，圆域分析的特征向量Vmean的均值、方差、歪度和峭度指标可分别由式(7)～式(10)求得。

(7)

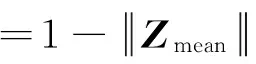
(8)

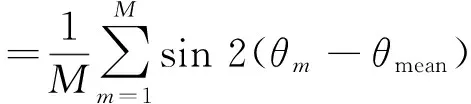
与轻质薄板相比，ALC板、AS装配式墙板的保温、隔热、防火性能较好。对比ALC板与AS装配式墙板，ALC板更多地是替代了传统建筑维护墙体，其缺点是强度低和本身不具备装饰性。AS装配式墙板的各项性能均非常优越，外墙板为混凝土清水色饰面，质感厚重大气，可作为墙体和外饰面使用，不需要做额外的外装饰。由于AS墙板安装方便，施工周期短和防水防火性能优越，也可用于露天防火墙和围墙。AS墙板全干作业且施工安装效率高，耐久性强，维护成本低，更符合装配式变电站的发展趋势。

(9)

(10)

需要注意的是，文献[15]仅仅分析了圆域0°～180°对应的时域振动信号，这就需要确保每段信号的起始点对应的回转支承的部位是相同的，否则每次分析结果只能对应回转支承半圈的区域，但是每次的区域可能都是不同的，这将使圆域分析的结果在时域上不具有任何物理意义，而从大量的振动数据中提取的每段信号都具有相同的相位显然是很困难的。仔细观察式(7)～式(10)可以发现，四个指标的计算结果与异常向量V1,V2,…,VM和特征向量Vmean各自的绝对角度是无关的。以图4为例，即使将圆域分析得到的异常向量统一转动一定角度，四个指标的计算结果并不会有所改变。利用这一特性，本文所取的每段时域信号都将对应着圆域0°～360°的范围，这样尽管每段信号的起始相位并不相同，但是完全不影响计算结果，且圆域分析的物理意义始终指向回转支承一整圈的健康状态，从而有效避免了信号相位同步的问题。

3 试验验证

3.1 加速寿命试验

为验证本文所提方法，研制出如图6所示回转支承试验台[21]对型号为QNA-730-22的内齿式回转支承进行了全寿命疲劳试验。为模拟实际工况，试验过程中，陪试回转支承的内圈(定圈)与底座相连，主试回转支承的内圈(动圈)通过工装与陪试回转支承的外圈(动圈)连接，主试回转支承的外圈(定圈)与上顶盖相连。这样，G1, G2两个油缸便可通过组合加载的方式将载荷加到上顶盖，再传递到主试回转支承，然后液压马达G3驱动陪试回转支承动圈，带动主试回转支承运行，从而模拟出实际工况下回转支承的运行。

根据某公司此型号回转支承承载能力曲线，主试回转支承被施以轴向力Fa=96 kN，倾覆力Mn=240 kNm的极限设计载荷，以4 r/min的转速进行满载荷疲劳寿命试验。试验过程中采用灵敏度为400 mV/g、响应频率0～1 kHz的Kistler-8315A010加速度传感器测量回转支承径向振动，并以2 kHz的采样率记录了其全寿命的振动信号。

疲劳寿命试验共进行了11天，试验进行到第7天上午时，出现了一根螺栓的疲劳断裂，此时进行了拆机，发现外圈(定圈)软带附近滚道由于疲劳已经出现了区域小幅滑移，内圈(动圈)上则是出现了轻微点蚀，分别如图7(a)和图7(b)所示。由于图中的初期故障并不影响回转支承继续服役，因此更换了失效的螺栓并加注了润滑脂后继续装机试验。至第11天试验结束时，回转支承已经完全失效卡死，外圈滚道出现了严重的疲劳剥落，部分滚珠甚至产生了疲劳断裂，如图7(c)所示。

(a) 试验7天后定圈滚道出现区域滑移

(b) 试验7天后动圈滚道出现点蚀

(c) 严重损坏的定圈滚道和滚珠

试验中回转支承的转速保持在4 r/min，因此圆域分析中每段信号对应回转支承转动一圈的时长应为15 s。据此，取每天6 h、12 h、18 h和24 h的4段信号，每段时长15 s，得到回转支承全寿命振动信号，如图8所示。

图8同时给出了试验第1天、第6天和第11天中各1 s的振动信号。可以看出，振动信号幅值在试验过程中基本保持增长趋势，但自始至终很少出现幅值很高的冲击成分。此外，在试验初期，回转支承振动信号以高频噪声为主，几乎无法看到中低频成分；第6天信号中的高频噪声依然存在，但是已经可见部分中频成分；而第11天的振动信号中则是以低频为主，中高频噪声已经基本不可见。这些现象与前文的分析是一致的，即回转支承运行初期振动信号基本被白噪声覆盖，当回转支承产生初始故障后，信号中会出现能量较低的冲击成分，后期随着故障进一步加剧，冲击成分能量会不断升高，信噪比也会持续提高。为进一步量化分析，对第6天和第11天的信号进行快速傅里叶变换(Fast Fourier Transform，FFT)，结果如图9所示。

(a) 全寿命信号

第1天第6天第11天

(b) 不同时段1 s信号

图8 回转支承全寿命振动信号

Fig.8 Life-cycle vibration signal of the tested slewing bearing

图9(a)展示的是第6天信号的频谱分析图，可以看到在<100 Hz处已经出现了部分的低频成分，但是>200 Hz的中高频噪声仍然占据主导；相对而言，图9(b)第11天信号的频谱中，100 Hz以下的低频成分能量非常高，而300 Hz以上的频率成分能量很微弱。此外，信号中频率为119 Hz的成分在试验初期能量很低，在第6天时能量达到最高，而在最后阶段能量又有所降低，这表明119 Hz可能是回转支承的某种初期故障产生的。

(a) 第6天信号的FFT

(b) 第11天信号的FFT

据此，根据图5选择w=4对每段15 s的时域振动信号进行圆域分析，由于每段信号的分析过程是完全相同的，此处仅以第6天和第10天各自的第1段信号为例进行讨论。为便于理解，将第6天的分析过程在时域内展开，而将第10天的分析过程在圆域内展开。

首先，将时域振动信号按秒均分成15个区域，同时将其映射到0°～360°的圆域中，每秒钟的时域信号对应24°的圆域信号，区域划分结果和转换后的圆域信号分别如图10和图12(a)所示；接着，令w=4，对每个角度区域的信号进行PAA，并在邻域相关图中输出用于椭圆拟合，分别如图11和图13所示；然后，判断每个拟合椭圆的倾角方向，将右倾斜椭圆所在的角度区域标记为异常向量或异常区域分别如图10和图12(b)所示，其中的红色向量即表示了异常向量的平均向量，也就是圆域分析的特征向量Vmean。

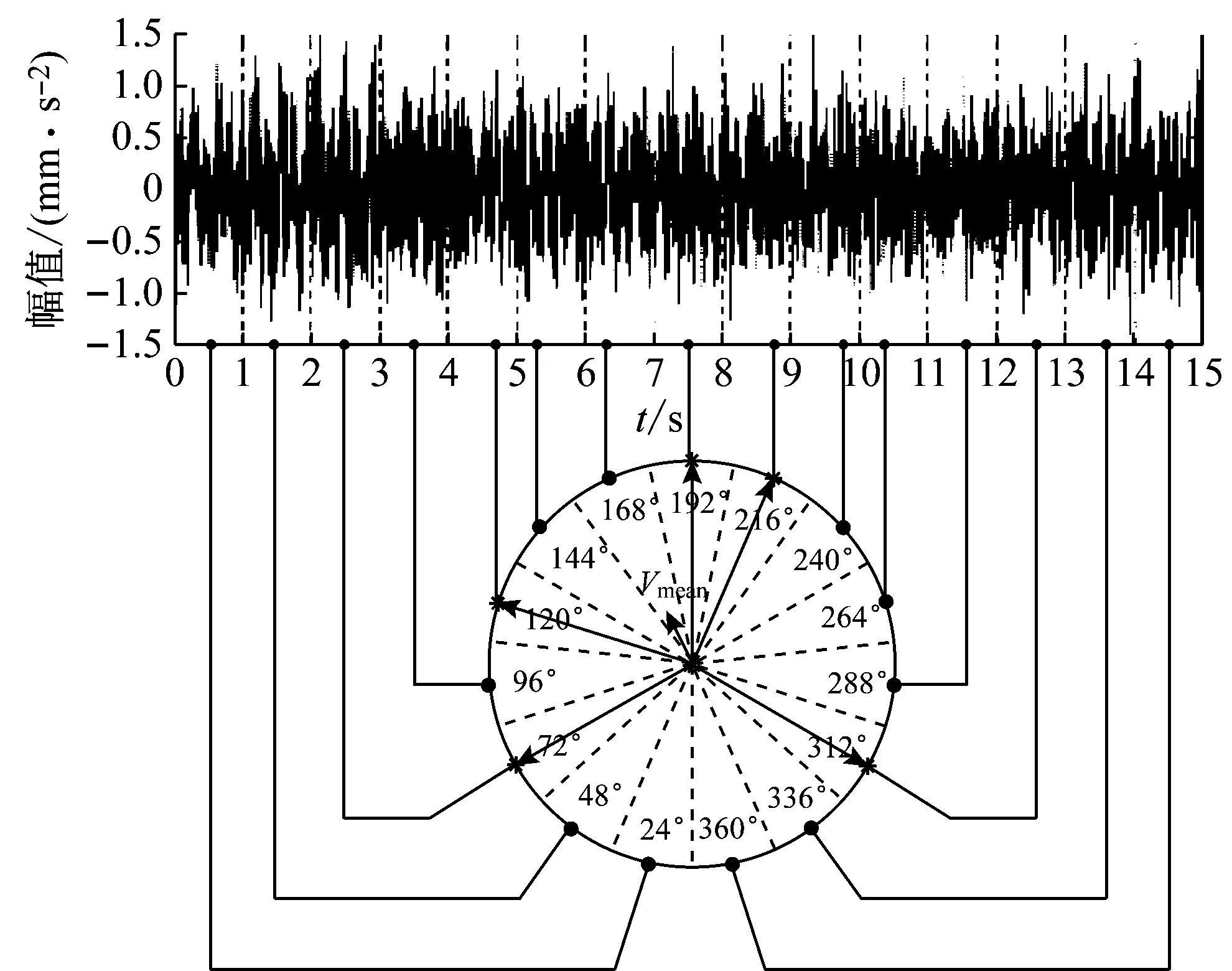
图10 第6天第1段信号的圆域分析(时域内展开)

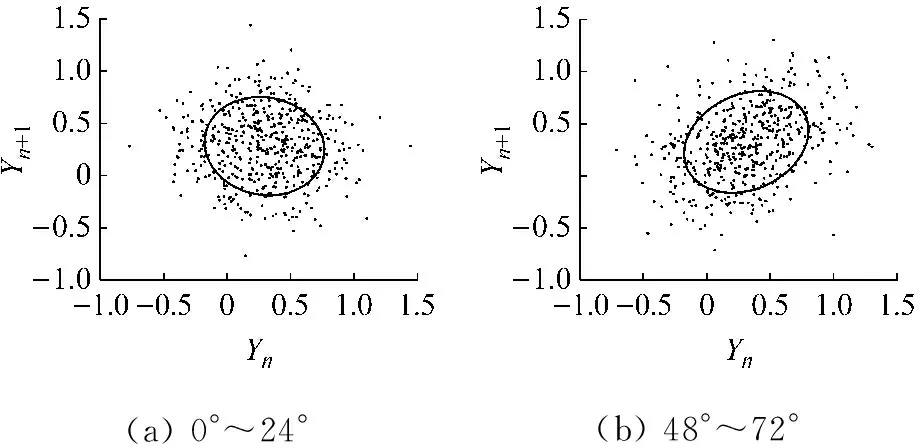
(a)0°～24°(b)48°～72°

图11 第6天第1段信号的部分拟合椭圆

图12 第10天第1段信号的圆域分析(圆域内展开)

图13 第10天第1段信号的部分拟合椭圆

Fig.13 Partial fitted ellipses of the 10th day

图11中的两个拟合椭圆离心率较小，椭圆更接近圆，且只是分别向左和向右有小幅度的倾斜，而图13中的两个拟合椭圆的离心率则大很多，倾斜角度也更大。由此可见，在回转支承寿命初期，各个角度区域的左倾斜拟合椭圆离心率和倾斜程度均逐步减小，初期故障产生后，拟合椭圆的倾角方向从左倾斜转换为右倾斜，随着故障进一步加剧，右倾斜椭圆的离心率不断增大。此外，由图10和图12(b)中可知，试验中期出现异常的角度区域较少，而试验后期异常区域较多，其特征向量Vmean的模长也越来越短。

据此，得到各段信号圆域分析的特征向量Vmean后，计算其均值、方差、歪度和峭度这4个指标在整个试验周期中的变化趋势，如图14所示。为进行对比分析，图14同时给出了原始振动信号[22]以及小波分析的相关时域指标。其中，小波分析利用db9小波将原始振动信号进行了3层分解，并选取第3层小波系数中的高频细分部分(D3)用于时域指标计算，具体方法此处不再赘述。

(a)均值(b)方差(c)歪度(d)峭度

图14 各项指标在整个寿命周期的变化

Fig.14 Four features of three different methods on the life cycle

由图14可知，部分指标在试验前两天有一定的波动，对应回转支承磨合阶段，两天后趋于平稳，回转支承正常运行，直到试验进行至第6天附近，圆域分析的各项指标均出现了较为明显的异常幅值，说明回转支承在试验进行到第6天时产生了初始故障，结合7天后拆机结果分析，定圈的区域滑移和动圈的点蚀应当是在此时产生的。相比之下，振动信号相关的时域特征在第6天附近几乎看不到明显的异常值，而小波分析结果的均值、方差和峭度指标中能观察到一定程度的异常产生，但是其可识别度远不如圆域分析的相关指标。由此可见，相对传统方法，圆域分析能够更准确地从高噪声、低信噪比的振动信号中诊断出回转支承的初始故障，便于工程人员提前制定有效的维护规划，缩短维护周期，从而降低维护成本。

4 结 论

回转支承实际工况下故障诊断方法的相关研究仍处于起步阶段，本文提出了一种圆域分析方法，将时域振动信号映射到圆域坐标系中，通过邻域相关图中拟合椭圆的倾角方向判断各角度区域是否异出现常，并将各异常向量的平均向量作为圆域分析的特征向量，最后以特征向量的均值、方差、歪度和峭度指标在整个寿命周期中的变化趋势进行故障诊断。加速寿命试验结果表明：大型回转支承早期的振动信号以高频噪声为主，中后期初始故障产生后中低频冲击成分不断增加；邻域相关离散点的拟合椭圆的倾角方向能够准确识别出信号中频率成分的变化，可以作为判断信号是否出现异常的依据；相比常用的时域特征和小波分析等方法，本方法能够更为准确地诊断出回转支承的初期故障，且故障点处的可识别度更高，分析结果的可解释性更强；将本方法用于回转支承状态监测，能够为制定及时准确的维护规划提供切实的参考依据，具有较强的工程应用价值。

[1] 回转支承：JB/T 2300—1999[S]. 北京: 机械科学研究院, 1999.

[2] WIDODO A, YANG B S. Machine health prognostics using survival probability and support vector machine[J]. Expert Systems with Applications, 2011, 38(7): 8430-8437.

[3] TAN A C C, KIM Y H, KOSSE V. Condition monitoring of low-speed bearings—a review[J]. Australian Journal of Mechanical Engineering, 2008, 6(1): 61-68.

[4] 张慧芳, 陈捷. 大型回转支承故障信号处理方法综述[J]. 机械设计与制造, 2012(3): 216-218.

ZHANG Huifang, CHEN Jie. Reserch on signal processing method of large slewing bearing[J]. Machinery Design & Manufacture, 2012(3): 216-218.

[5] ŽVOKELJ M, ZUPAN S, PREBIL I. Multivariate and multiscale monitoring of large-size low-speed bearings using ensemble empirical Mode decomposition method combined with principal component analysis[J]. Mechanical Systems and Signal Processing, 2010, 24(4): 1049-1067.

[6] ŽVOKELJ M, ZUPAN S, PREBIL I. Non-linear multivariate and multiscale monitoring and signal denoising strategy using kernel principal component analysis combined with ensemble empirical Mode decomposition method[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2631-2653.

[7] 郭刚涛, 秦文科, 李婧铱, 等. 基于混沌理论的大口径天线回转支承故障诊断研究[J]. 机械工程师, 2015(2): 133-135.

GUO Gangtao, QIN Wenke, LI Jingyi, et al. Fault diagnosis of large-diameter antenna slewing bearing based on chaos theory[J]. Mechanical Engineer, 2015(2): 133-135.

[8] 赵阳, 陈捷, 洪荣晶, 等. EMD 和独立分量分析在转盘轴承故障诊断中的应用[J]. 轴承, 2015 (7): 54-59.

ZHAO Yang, CHEN Jie, HONG Rongjing, et al. Application of EMD and ICA in fault diagnosis for slewing bearings[J]. Bearing, 2015 (7): 54-59.

[9] 杨杰, 陈捷, 徐新庭, 等. 基于小波-能量模式的回转支承故障诊断方法研究与应用[J]. 南京工业大学学报(自然科学版), 2015, 37(4): 134-140.

YANG Jie, CHEN Jie, XU Xinting, et al. Slewing bearing analysis on fault diagnosis based on wavelet and energy fault mode and its application[J]. Journal of Nanjing Tech University (Natural Science), 2015, 37(4): 134-140.

[10] BONNARDOT F, RANDALL R B, ANTONI J. Enhanced unsupervised noise cancellation using angular resampling for planetary bearing fault diagnosis[J]. International Journal of Acoustics and Vibrations, 2004, 9(2): 51-60.

[11] RENAUDIN L, BONNARDOT F, MUSY O, et al. Natural roller bearing fault detection by angular measurement of true instantaneous angular speed[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 1998-2011.

[12] VILLA L F, RENONES A, PERAN J R, et al. Angular resampling for vibration analysis in wind turbines under non-linear speed fluctuation[J]. Mechanical Systems and Signal Processing, 2011, 25(6): 2157-2168.

[13] VILLA L F, RENONES A, PERAN J R, et al. Statistical fault diagnosis based on vibration analysis for gear test-bench under non-stationary conditions of speed and load[J]. Mechanical Systems and Signal Processing, 2012, 29(5): 436-446.

[14] BONNARDOT F, BADAOUI M E, RANDALL R B, et al. Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation)[J]. Mechanical Systems and Signal Processing, 2005, 19(4): 766-785.

[15] CAESARENDRA W, KOSASIH B, TIEU A K, et al. Circular domain features based condition monitoring for low speed slewing bearing[J]. Mechanical Systems and Signal Processing, 2014, 45(1): 114-138.

[16] YI B K, FALOUTSOS C. Fast time sequence indexing for arbitrary Lp norms[EB/OL].[2015-12-14].http://repository.cmu.edu/compsci/553/.

[17] FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 476-480.

[18] LUO M F, MATHEW J. Monitoring machinery with varying speed using angle domain analysis[C]// 1993 Proceedings of 17th Annual Meeting. St Louis: Vibration Institute, 1993: 69-78.

[19] BOSSLEY K M, MCKENDRICK R J, HARRIS C J, et al. Hybrid computed order tracking[J]. Mechanical Systems and Signal Processing, 1999, 13(4): 627-641.

[20] PEWSEY A. The large-sample joint distribution of key circular statistics[J]. Metrika, 2004, 60(1): 25-32.

[21] 黄筱调, 王华, 陈捷, 等. 风电转盘轴承综合性能实验台：CN100587444C[P]. 2010-02-03.

[22] 王小玲, 陈进, 从飞云. 基于时频的频带熵方法在滚动轴承故障识别中的应用[J]. 振动与冲击, 2012, 31(18): 29-33.

WANG Xiaoling, CHEN Jin, CONG Yunfei. Application of spectral band entropy (SBE) method in rolling bearing fault diagnosis based on time-frequency analysis[J]. Journal of Vibration and Shock, 2012, 31(18): 29-33.

Incipient fault diagnosis of large-size slewing bearings based on circular domain analysis

FENG Yang, HUANG Xiaodiao, HONG Rongjing, CHEN Jie

(School of Mechanical and Power Engineering, Nanjing Tech University, Nanjing 210009, China)

The background noise of a slewing bearing vibration signal in practical load cases is very high, it makes commonly used fault detection approaches not suitable for slewing bearing fault diagnosis. Therefore, a novel signal processing method was proposed based on circular domain analysis. First of all, the time domain signal was transformed into a circular domain and the transformed signal was divided into several zones according to a certain angle, and then the neighborhood correlation discrete points of each zone were fitted as an ellipse. Afterwards, the ellipses skewing to the right were tagged as abnormalities and the corresponding abnormal vectors were obtained based on the whole cycle of a slewing bearing. Finally, the characteristic vector of circular domain analysis, also the mean vector of all the abnormal vectors was acquired, and its mean, variance, skewness and kurtosis were calculated and taken as the fault indicators. An accelerated life test was conducted on a slewing bearing to validate the proposed method. Results showed that the proposed method has a better performance to detect an incipient fault, such as, slipping and pitting in the raceway than the time domain analysis and the wavelet analysis do, it can be an effective tool for slewing bearing fault diagnosis in engineering practice.

slewing bearing; circular analysis; circular resampling; fault diagnosis; accelerated life test

国家自然科学基金项目(51375222；51175242)

2015-12-17 修改稿收到日期：2016-03-16

封杨 男，博士生，1988年生

黄筱调 男，教授，博士生导师，1952年生

TP206.3

A

10.13465/j.cnki.jvs.2017.09.017